2024-2025学年七年级下学期数学期考末模拟卷(浙江诸暨市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期考末模拟卷(浙江诸暨市专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 228.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 12:31:45 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期末模拟卷(诸暨市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列运算正确的是( )
A. B. C. D.
2.若 则 用只含 的代数式表示为( )
A. B. C. D.
3. 若关于 的分式方程 无解,则 的值为( )
A.0 B.3
C.1 或 D.0 或 1 或
4.如图所示,点E在的延长线上,下列条件中,能判断的是( )
A. B.
C. D.
5.如图,下列不能判定的条件是( )
A. B.
C. D.
6.如图,某校八年级某班的全体同学最喜欢的球类运动用的扇形统计图来表示,下面说法中错误的是( )
A.喜欢足球的人数最多
B.喜欢乒乓球的人数占全班总人数的25%
C.喜欢排球的人数占全班总人数的
D.喜欢足球的人数是喜欢篮球的人数的2倍
7. 使 乘积中不含 与 项,则 的值为( )
A.-8 B.-4 C.-2 D.8
8.我国古代数学名著《九章算术》中记载:今有甲乙两人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?意思是现有甲乙两人,都不知道有多少钱,若乙把他一半的钱给甲,则甲有50钱;而甲把他的钱给乙,则乙有50钱,问甲、乙各有多少钱?如果设甲原来有x钱,乙原来有y钱,则可列方程组为( )
A. B.
C. D.
9.我们知道,同底数幂的乘法法则为(其中,,为正整数).类似地,我们规定关于任意正整数,的一种新运算:.若,那么的结果是( )
A. B. C. D.
10.将一副三角板如图放置,则下列结论中,正确的是( )
①;②如果,则有;③如果,则有;④如果,则有.
A.①②③④ B.③④ C.①②④ D.①②③
二、填空题(本题有8小题,每小题3分,共25分)
11.若关于x的代数式x2-2mx+4(m是常数)是一个完全平方式,则m= .
12.关于的分式方程有增根,则的值是 .
13. 若分式 有意义,则 应满足的条件是
14.将两个边长分别为a和b的正方形按图1所示方式放置,其未叠合部分(阴影部分)的面积为S1,周长为再在图1中大正方形的右下角摆放一个边长为b的小正方形,如图2,两个小正方形叠合部分(阴影部分)的面积为S2,周长为.若=48,ab=13,则S1+S2=. .
15. 如图, 两个大小相同的直角三角形重叠在一起, 若 固定不动, 将另一个三角形向左平移 3 cm 并记为 , 其中 与 相交于点 . 若 , 则 的面积为 .
16.通过以下方法可将转化为方程,我们规定:方程称为的还原方程.
去分母,
移项,
两边平方,
整理,
(1)的还原方程是 .
(2)若,则代数式 .
17.不改变分式的值,把它的分子和分母中的各项系数都化成整数,则得到的结果为 .
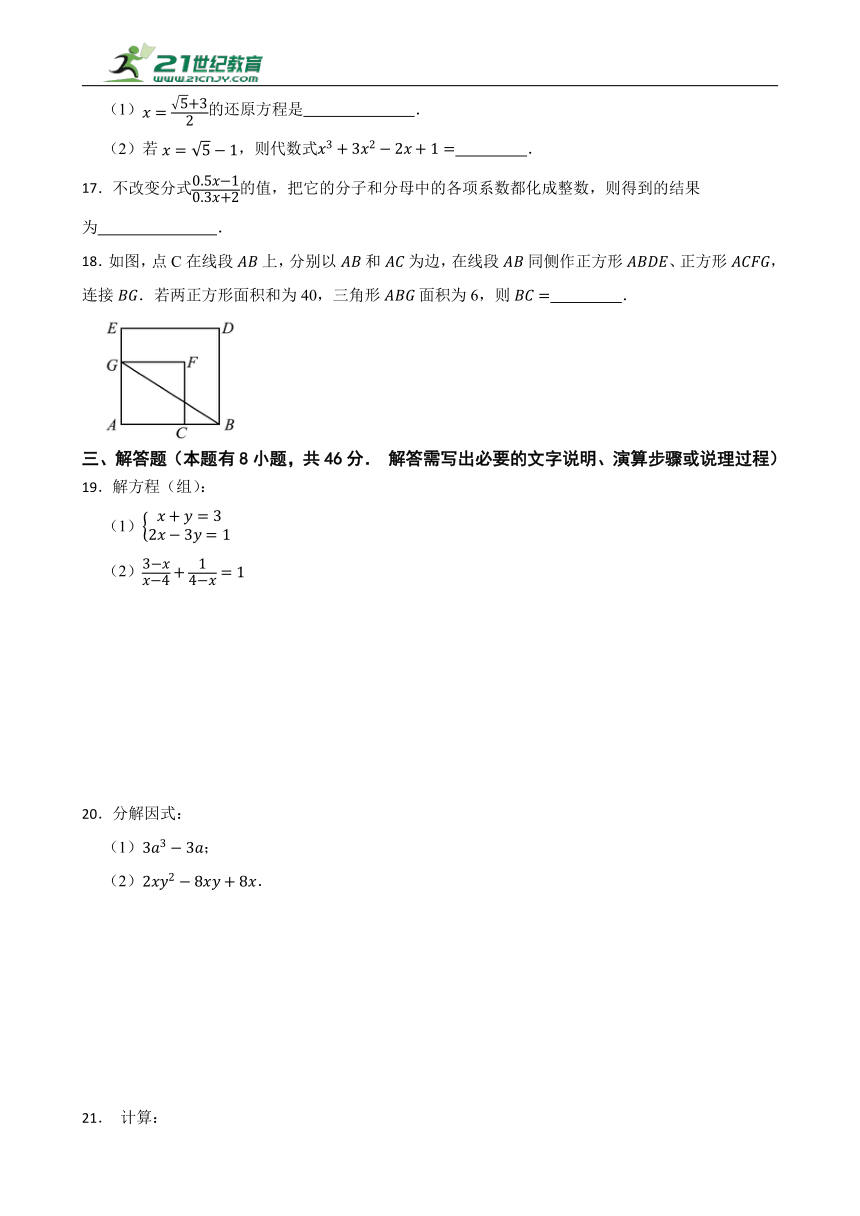
18.如图,点C在线段上,分别以和为边,在线段同侧作正方形、正方形,连接.若两正方形面积和为40,三角形面积为6,则 .
三、解答题(本题有8小题,共46分. 解答需写出必要的文字说明、演算步骤或说理过程)
19.解方程(组):
(1)
(2)
20.分解因式:
(1);
(2).
21. 计算:
(1)
(2)
22.先化简,再求值:
(1),其中.
(2),其中,.
23.如图,已知在三角形中,点D,E分别在上,.连结,点F在上,.
(1)求证:;
(2)若平分,求的度数.
24.某校为了解学生一分钟跳绳个数情况,随机抽取了60名学生进行调查,获得每位学生一分钟跳绳个数(单位:个),下面是对数据进行整理、描述和分析后的部分信息.
信息1.一分钟跳绳个数的频数分布直方图如图,数据分成4组:,,,;
信息2.一分钟跳绳个数在这一组的有:182,189,182,180,186,185,183,184,188,185,183,185,186,183,186,184,188,180.根据以上信息,回答下列问题:
(1)求出频数分布直方图中m的值;
(2)求这60个数据的组距及跳绳成绩为“186个”的频率;
(3)该校规定跳绳一分钟180个及以上为良好,若该校有1200名学生,请估计该校学生跳绳达到良好的人数.
25.如图,将一张长方形纸片按如图所示分割成6块,其中有两块是边长为的正方形,一块是边长为的正方形().
(1)观察图形,代数式可因式分解为______;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
①用含的代数式表示;
②若,求的值.
26. 根据以下素材,探索完成任务.
奖品购买方案设计
素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的1.5倍,用108元购买钢笔的数量比用60元购买笔记本的数量多2件.
素材2 某学校花费540元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”,购买的钢笔数量比笔记本少15支.
素材3 学校花费540元后,文具店赠送m张(1≤m<10)兑换券(如图)用于商品兑换.兑换后,笔记本数量与钢笔相同.
问题解决
任务一 【探求商品单价】请运用适当方法,求出钢笔与笔记本的单价.
任务二 【探究购买方案】在不使用兑换券的情况下,求购买的钢笔和笔记本数量.
任务三 【确定兑换方式】运用数学知识,确定兑换方案.
答案解析部分
1.D
解:A:,所以A不正确;
B:,所以B不正确;
C:,所以C不正确;
D: ,所以D正确。
故答案为:D.
根据幂的有关运算法则分别进行正确计算,即可得出答案。
2.B
解:∵x=3-m,
∴m=3-x.
∴y=1+2(3-x)=7-2x.
故答案为:B
先根据x=3-m,表示出m,再代入y=1+2m即可得到y关于x的代数式.
3.C
4.D
解:A.∠3和∠4是直线BD,AC被直线BC所截形成的内错角,故可得,故选项A不符合题意;
B. ∠1和∠4是直线AB,AC被直线BC所截形成的同旁内角,故得不到,故选项B不符合题意;
C.∠D和∠DCE是直线BD,AC被直线DC所截形成的内错角,故可得,故选项C不符合题意;
D.∠D和∠ABD是直线AB,CD被直线BD所截形成的同旁内角,故可得,故选项D符合题意;
故答案:D.
根据平行线的判定定理和同位角,内错角,同旁内角的定义进行判断即可.
5.B
6.C
解:∵40%>25%>20%>15%,
故喜欢足球的人数最多,故选项A正确,不符合题意;
从扇形统计图可得,喜欢乒乓球的人数占全等总人数的25%,故选项B正确,不符合题意;
喜欢排球的人数占全班总人数的15%,,故选项C说法错误,符合题意;
从扇形统计图可得,喜欢足球的人数占全等总人数的40%,喜欢篮球的人数占总人数的20%,且40%=20%×2,故选项D说法正确,不符合题意.
故答案为:C
观察扇形统计图,比较即可判断选项A;读数即可判断选项B,将百分数转化成分数,即可判断选项C,计算可判断选项D.
7.D
解: =x4+(3-q)x3+(4-3q+p)x2+(12-pq)x+4p,
∵ 乘积中不含 与 项,
∴4-3q+p=0,3-q=0,
∴p=5,q=3,
∴p+q=8.
故答案为:D.
首先根据多项式乘多项式法则进行整式的乘法运算得出 x4+(3-q)x3+(4-3q+p)x2+(12-pq)x+4p,然后根据乘积中不含x2与x3项,可得出4-3q+p=0,3-q=0,解方程组,可得出p=5,q=3,进一步即可得出p+q=8.
8.B
解:设甲原来有x钱,乙原来有y钱,由题意可得.
故答案为:B.
根据乙把他一半的钱给甲,则甲有50钱可得x+y=50;根据甲把他的钱给乙,则乙有50钱可得y+x=50,联立即可得到方程组.
9.D
解:∵,,
∴.
故答案为:D.
根据新定义将进行分解,再根据同底数幂的运算求解即可.
10.D
解:∵∠CAB+∠DAE=180°,
∴∠1+∠2+∠2+∠3=180°,即∠1+2∠2+∠3=180°,故①正确;
∵BC∥DA,
∴∠3=∠B=45°,
∴∠2=90°-∠3=45°,故②正确;
∵∠3=60°,
∴∠2=90°-60°=30°,∠1=90°-∠2=60°,
∴∠E=∠1,
∴AC∥DE,故③正确;
∵∠1+∠3=90°,∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3=45°,
∴∠3=∠B,
∴AD∥BC,
∴∠4=∠D=30°,故④错误.
故答案为:D.
根据三角板中的角度进行计算即可得∠CAB+∠DAE=180°即可判断①;根据平行线得性质可得∠3=∠B,可得∠2=90°-∠3=45°,即可判断② ;根据∠3=60°,可得∠1=60°,进而根据内错角相等即可判断③ ;根据题意可得∠3=45°,进而可得AD∥BC,则∠4=30°,即可判断④ .
11.±2
解:∵是完全平方式,
∴,
∴.
故答案为:.
根据首末两项分别是x和2的平方,可得中间一项为加上或减去它们乘积的2倍,即可求出m的值.
12.1
解:∵,
∴去分母,得:;
解得:x=-a+4,
∵分式方程有增根,增根为:x=3,
∴-a+4=3,
解得:a=1,
故答案为:1.
解分式方程得到:x=-a+4,确定方程的增根x=3,然后把x=3代入建立关于a的方程,求解即可。
13.
解:分式有意义,
,
,
故答案为:.
根据分式有意义的条件:分母不等于零,据此求解.
14.77
由图可知:,
,
∵=6b-2a
∴=6a-6b=48
∴a﹣b=8,ab=13,
∴S1+S2=a2+b2﹣ab=(a﹣b)2+ab=64+13=77;
先计算出S1,S2,l1,l2,根据完全平方公式变形计算S1+S2的值,正确理解图形及掌握完全平方公式是解题的关键.
15.9
解:由平移的性质可得:
CF=BE,DE=AB,
∵AB=5cm,BC=9cm,DH=2cm,
∴CE=BC -BE=9-3=6,EH=DE-DH=5-2=3,
∴S△CEH=×CE×EH=×6×3=9.
故答案为:9.
由平移的性质可得:CF=BE,DE=AB,由线段的构成CE=BC -BE、EH=DE-DH可求出CE、EH的值,然后根据三角形的面积公式S△CEH=×CE×EH可求解.
16.;5
17.
解:.
利用分式的性质,分子、分母同时乘以10解题即可.
18.4
19.(1)解:,
得:,
解得:,
把代入①得:,
解得:,
则方程组的解为;
(2)解:
去分母得:,
解得:,
检验:把代入得:,
所以是原方程的解.
(1)利用加减消元法求出解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,再检验即可.
20.(1)解:原式
;
(2)解:原式
.
(1)先提公因式3a,再用平方差公式分解即可;
(2)先提公因式2x,再用完全平方公式分解即可.
21.(1)解:,
,
;
(2)解:,
,
.
(1)先利用有理数的乘方,零指数幂,负整数指数幂的运算法则分别进行运算,再进行加减运算,即可解题;
(2)先利用平方差公式,以及完全平方公式进行计算,再合并同类项即可.
22.(1)解:
;
当时,原式;
(2)解:
;
当,时,原式.
(1)利用整式乘法法则展开,再合并同类项,最后代值即可求解;
(2)按照运算顺序先算括号,再算除法,化简后把a、b的值代入即可求解.
(1)解:
;
当时,原式;
(2)解:
;
当,时,原式.
23.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴的度数为.
(1)根据两直线平行,同位角相等得到,即可得到,利用内错角相等,两直线平行得到结论即可;
(2)根据角平分线的定义得到,即可得到,然后利用平角得定义求出∠B的值,即可得到∠ADC的值,然后根据平行线的性质解答即可.
24.(1)解:根据频数分布直方图可得.
(2)解:由题意可知:组距为170-160=10,
跳绳成绩为“186个”的频率.
(3)解:
答:该校学生跳绳达到良好的估计有640人.
(1)利用频数之和等于总数,求出m的值;
(2)先利用图中分组确定组距,再用频数除以总数求出频率;
(3)用1200乘以良好所占的比例.
25.(1)
(2)①;②1
26.解:任务一:设笔记本每本x元,则钢笔每支1.5x元.
由题意得,
解得:x=6
经检验,是原方程的解,且符合题意.
6×1.5=9(元)
答:每支钢笔9元,每本笔记本6元.
任务二:设购买钢笔a支,购买笔记本b本.
由题意得,解得
答:购买钢笔30支,笔记本45本.
任务三:设其中y张用来兑换钢笔,则(m-y)张兑换笔记本.
由题意得:30+5y=45+10(m-y), 整理得:,
∵1≤m<10
∴或或,
∴有3种方案,分别为:
①3张兑换钢笔,0张兑换笔记本;
②5张兑换钢笔,1张兑换笔记本;
③7张兑换钢笔,2张兑换笔记本.
任务一:基本关系:金额=价格×数量,设笔记本每本x元,则钢笔每支1.5x元.由题意,列出方程,即可求解;
任务二:设购买钢笔a支,购买笔记本b本.由题意,列出方程组,即可求解;
任务三:设其中y张用来兑换钢笔,则(m-y)张兑换笔记本.由题意,列出分式方程,即可求解.
2024-2025学年七年级下册期末模拟卷(诸暨市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列运算正确的是( )
A. B. C. D.
2.若 则 用只含 的代数式表示为( )
A. B. C. D.
3. 若关于 的分式方程 无解,则 的值为( )
A.0 B.3
C.1 或 D.0 或 1 或
4.如图所示,点E在的延长线上,下列条件中,能判断的是( )
A. B.
C. D.
5.如图,下列不能判定的条件是( )
A. B.
C. D.
6.如图,某校八年级某班的全体同学最喜欢的球类运动用的扇形统计图来表示,下面说法中错误的是( )
A.喜欢足球的人数最多
B.喜欢乒乓球的人数占全班总人数的25%
C.喜欢排球的人数占全班总人数的
D.喜欢足球的人数是喜欢篮球的人数的2倍
7. 使 乘积中不含 与 项,则 的值为( )
A.-8 B.-4 C.-2 D.8
8.我国古代数学名著《九章算术》中记载:今有甲乙两人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?意思是现有甲乙两人,都不知道有多少钱,若乙把他一半的钱给甲,则甲有50钱;而甲把他的钱给乙,则乙有50钱,问甲、乙各有多少钱?如果设甲原来有x钱,乙原来有y钱,则可列方程组为( )
A. B.
C. D.
9.我们知道,同底数幂的乘法法则为(其中,,为正整数).类似地,我们规定关于任意正整数,的一种新运算:.若,那么的结果是( )
A. B. C. D.
10.将一副三角板如图放置,则下列结论中,正确的是( )
①;②如果,则有;③如果,则有;④如果,则有.
A.①②③④ B.③④ C.①②④ D.①②③
二、填空题(本题有8小题,每小题3分,共25分)
11.若关于x的代数式x2-2mx+4(m是常数)是一个完全平方式,则m= .
12.关于的分式方程有增根,则的值是 .
13. 若分式 有意义,则 应满足的条件是
14.将两个边长分别为a和b的正方形按图1所示方式放置,其未叠合部分(阴影部分)的面积为S1,周长为再在图1中大正方形的右下角摆放一个边长为b的小正方形,如图2,两个小正方形叠合部分(阴影部分)的面积为S2,周长为.若=48,ab=13,则S1+S2=. .
15. 如图, 两个大小相同的直角三角形重叠在一起, 若 固定不动, 将另一个三角形向左平移 3 cm 并记为 , 其中 与 相交于点 . 若 , 则 的面积为 .
16.通过以下方法可将转化为方程,我们规定:方程称为的还原方程.
去分母,
移项,
两边平方,
整理,
(1)的还原方程是 .
(2)若,则代数式 .
17.不改变分式的值,把它的分子和分母中的各项系数都化成整数,则得到的结果为 .
18.如图,点C在线段上,分别以和为边,在线段同侧作正方形、正方形,连接.若两正方形面积和为40,三角形面积为6,则 .
三、解答题(本题有8小题,共46分. 解答需写出必要的文字说明、演算步骤或说理过程)
19.解方程(组):
(1)
(2)
20.分解因式:
(1);
(2).
21. 计算:
(1)
(2)
22.先化简,再求值:
(1),其中.
(2),其中,.
23.如图,已知在三角形中,点D,E分别在上,.连结,点F在上,.
(1)求证:;
(2)若平分,求的度数.
24.某校为了解学生一分钟跳绳个数情况,随机抽取了60名学生进行调查,获得每位学生一分钟跳绳个数(单位:个),下面是对数据进行整理、描述和分析后的部分信息.
信息1.一分钟跳绳个数的频数分布直方图如图,数据分成4组:,,,;
信息2.一分钟跳绳个数在这一组的有:182,189,182,180,186,185,183,184,188,185,183,185,186,183,186,184,188,180.根据以上信息,回答下列问题:
(1)求出频数分布直方图中m的值;
(2)求这60个数据的组距及跳绳成绩为“186个”的频率;
(3)该校规定跳绳一分钟180个及以上为良好,若该校有1200名学生,请估计该校学生跳绳达到良好的人数.
25.如图,将一张长方形纸片按如图所示分割成6块,其中有两块是边长为的正方形,一块是边长为的正方形().
(1)观察图形,代数式可因式分解为______;
(2)图中阴影部分面积之和记作,非阴影部分面积之和记作.
①用含的代数式表示;
②若,求的值.
26. 根据以下素材,探索完成任务.
奖品购买方案设计
素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的1.5倍,用108元购买钢笔的数量比用60元购买笔记本的数量多2件.
素材2 某学校花费540元购买该文具店的钢笔和笔记本作为奖品颁发给“优秀学生”,购买的钢笔数量比笔记本少15支.
素材3 学校花费540元后,文具店赠送m张(1≤m<10)兑换券(如图)用于商品兑换.兑换后,笔记本数量与钢笔相同.
问题解决
任务一 【探求商品单价】请运用适当方法,求出钢笔与笔记本的单价.
任务二 【探究购买方案】在不使用兑换券的情况下,求购买的钢笔和笔记本数量.
任务三 【确定兑换方式】运用数学知识,确定兑换方案.
答案解析部分
1.D
解:A:,所以A不正确;
B:,所以B不正确;
C:,所以C不正确;
D: ,所以D正确。
故答案为:D.
根据幂的有关运算法则分别进行正确计算,即可得出答案。
2.B
解:∵x=3-m,
∴m=3-x.
∴y=1+2(3-x)=7-2x.
故答案为:B
先根据x=3-m,表示出m,再代入y=1+2m即可得到y关于x的代数式.
3.C
4.D
解:A.∠3和∠4是直线BD,AC被直线BC所截形成的内错角,故可得,故选项A不符合题意;
B. ∠1和∠4是直线AB,AC被直线BC所截形成的同旁内角,故得不到,故选项B不符合题意;
C.∠D和∠DCE是直线BD,AC被直线DC所截形成的内错角,故可得,故选项C不符合题意;
D.∠D和∠ABD是直线AB,CD被直线BD所截形成的同旁内角,故可得,故选项D符合题意;
故答案:D.
根据平行线的判定定理和同位角,内错角,同旁内角的定义进行判断即可.
5.B
6.C
解:∵40%>25%>20%>15%,
故喜欢足球的人数最多,故选项A正确,不符合题意;
从扇形统计图可得,喜欢乒乓球的人数占全等总人数的25%,故选项B正确,不符合题意;
喜欢排球的人数占全班总人数的15%,,故选项C说法错误,符合题意;
从扇形统计图可得,喜欢足球的人数占全等总人数的40%,喜欢篮球的人数占总人数的20%,且40%=20%×2,故选项D说法正确,不符合题意.
故答案为:C
观察扇形统计图,比较即可判断选项A;读数即可判断选项B,将百分数转化成分数,即可判断选项C,计算可判断选项D.
7.D
解: =x4+(3-q)x3+(4-3q+p)x2+(12-pq)x+4p,
∵ 乘积中不含 与 项,
∴4-3q+p=0,3-q=0,
∴p=5,q=3,
∴p+q=8.
故答案为:D.
首先根据多项式乘多项式法则进行整式的乘法运算得出 x4+(3-q)x3+(4-3q+p)x2+(12-pq)x+4p,然后根据乘积中不含x2与x3项,可得出4-3q+p=0,3-q=0,解方程组,可得出p=5,q=3,进一步即可得出p+q=8.
8.B
解:设甲原来有x钱,乙原来有y钱,由题意可得.
故答案为:B.
根据乙把他一半的钱给甲,则甲有50钱可得x+y=50;根据甲把他的钱给乙,则乙有50钱可得y+x=50,联立即可得到方程组.
9.D
解:∵,,
∴.
故答案为:D.
根据新定义将进行分解,再根据同底数幂的运算求解即可.
10.D
解:∵∠CAB+∠DAE=180°,
∴∠1+∠2+∠2+∠3=180°,即∠1+2∠2+∠3=180°,故①正确;
∵BC∥DA,
∴∠3=∠B=45°,
∴∠2=90°-∠3=45°,故②正确;
∵∠3=60°,
∴∠2=90°-60°=30°,∠1=90°-∠2=60°,
∴∠E=∠1,
∴AC∥DE,故③正确;
∵∠1+∠3=90°,∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3=45°,
∴∠3=∠B,
∴AD∥BC,
∴∠4=∠D=30°,故④错误.
故答案为:D.
根据三角板中的角度进行计算即可得∠CAB+∠DAE=180°即可判断①;根据平行线得性质可得∠3=∠B,可得∠2=90°-∠3=45°,即可判断② ;根据∠3=60°,可得∠1=60°,进而根据内错角相等即可判断③ ;根据题意可得∠3=45°,进而可得AD∥BC,则∠4=30°,即可判断④ .
11.±2
解:∵是完全平方式,
∴,
∴.
故答案为:.
根据首末两项分别是x和2的平方,可得中间一项为加上或减去它们乘积的2倍,即可求出m的值.
12.1
解:∵,
∴去分母,得:;
解得:x=-a+4,
∵分式方程有增根,增根为:x=3,
∴-a+4=3,
解得:a=1,
故答案为:1.
解分式方程得到:x=-a+4,确定方程的增根x=3,然后把x=3代入建立关于a的方程,求解即可。
13.
解:分式有意义,
,
,
故答案为:.
根据分式有意义的条件:分母不等于零,据此求解.
14.77
由图可知:,
,
∵=6b-2a
∴=6a-6b=48
∴a﹣b=8,ab=13,
∴S1+S2=a2+b2﹣ab=(a﹣b)2+ab=64+13=77;
先计算出S1,S2,l1,l2,根据完全平方公式变形计算S1+S2的值,正确理解图形及掌握完全平方公式是解题的关键.
15.9
解:由平移的性质可得:
CF=BE,DE=AB,
∵AB=5cm,BC=9cm,DH=2cm,
∴CE=BC -BE=9-3=6,EH=DE-DH=5-2=3,
∴S△CEH=×CE×EH=×6×3=9.
故答案为:9.
由平移的性质可得:CF=BE,DE=AB,由线段的构成CE=BC -BE、EH=DE-DH可求出CE、EH的值,然后根据三角形的面积公式S△CEH=×CE×EH可求解.
16.;5
17.
解:.
利用分式的性质,分子、分母同时乘以10解题即可.
18.4
19.(1)解:,
得:,
解得:,
把代入①得:,
解得:,
则方程组的解为;
(2)解:
去分母得:,
解得:,
检验:把代入得:,
所以是原方程的解.
(1)利用加减消元法求出解;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,再检验即可.
20.(1)解:原式
;
(2)解:原式
.
(1)先提公因式3a,再用平方差公式分解即可;
(2)先提公因式2x,再用完全平方公式分解即可.
21.(1)解:,
,
;
(2)解:,
,
.
(1)先利用有理数的乘方,零指数幂,负整数指数幂的运算法则分别进行运算,再进行加减运算,即可解题;
(2)先利用平方差公式,以及完全平方公式进行计算,再合并同类项即可.
22.(1)解:
;
当时,原式;
(2)解:
;
当,时,原式.
(1)利用整式乘法法则展开,再合并同类项,最后代值即可求解;
(2)按照运算顺序先算括号,再算除法,化简后把a、b的值代入即可求解.
(1)解:
;
当时,原式;
(2)解:
;
当,时,原式.
23.(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴的度数为.
(1)根据两直线平行,同位角相等得到,即可得到,利用内错角相等,两直线平行得到结论即可;
(2)根据角平分线的定义得到,即可得到,然后利用平角得定义求出∠B的值,即可得到∠ADC的值,然后根据平行线的性质解答即可.
24.(1)解:根据频数分布直方图可得.
(2)解:由题意可知:组距为170-160=10,
跳绳成绩为“186个”的频率.
(3)解:
答:该校学生跳绳达到良好的估计有640人.
(1)利用频数之和等于总数,求出m的值;
(2)先利用图中分组确定组距,再用频数除以总数求出频率;
(3)用1200乘以良好所占的比例.
25.(1)
(2)①;②1
26.解:任务一:设笔记本每本x元,则钢笔每支1.5x元.
由题意得,
解得:x=6
经检验,是原方程的解,且符合题意.
6×1.5=9(元)
答:每支钢笔9元,每本笔记本6元.
任务二:设购买钢笔a支,购买笔记本b本.
由题意得,解得
答:购买钢笔30支,笔记本45本.
任务三:设其中y张用来兑换钢笔,则(m-y)张兑换笔记本.
由题意得:30+5y=45+10(m-y), 整理得:,
∵1≤m<10
∴或或,
∴有3种方案,分别为:
①3张兑换钢笔,0张兑换笔记本;
②5张兑换钢笔,1张兑换笔记本;
③7张兑换钢笔,2张兑换笔记本.
任务一:基本关系:金额=价格×数量,设笔记本每本x元,则钢笔每支1.5x元.由题意,列出方程,即可求解;
任务二:设购买钢笔a支,购买笔记本b本.由题意,列出方程组,即可求解;
任务三:设其中y张用来兑换钢笔,则(m-y)张兑换笔记本.由题意,列出分式方程,即可求解.
同课章节目录
