6.2 第2课时 利用四边形对角线的性质判定 课件(共46张PPT)
文档属性
| 名称 | 6.2 第2课时 利用四边形对角线的性质判定 课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 00:00:00 | ||
图片预览









文档简介
(共46张PPT)
北师大版数学八年级下册
第六章 平行四边形
汇报人:孙老师
汇报班级:X级X班
6.2 第2课时 利用四边形对角线的性质判定
2 平行四边形的判定
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
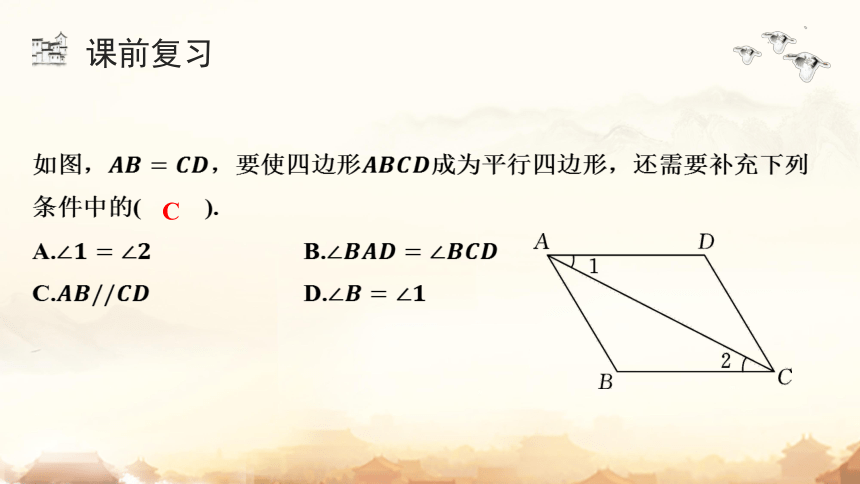
课前复习
如图,,要使四边形 成为平行四边形,还需要补充下列
条件中的( ).
C
A. B.
C. D.
第贰章节
新课导入
新课导入
前面我们已经知道:
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
你还能找到其他的判定方法吗?
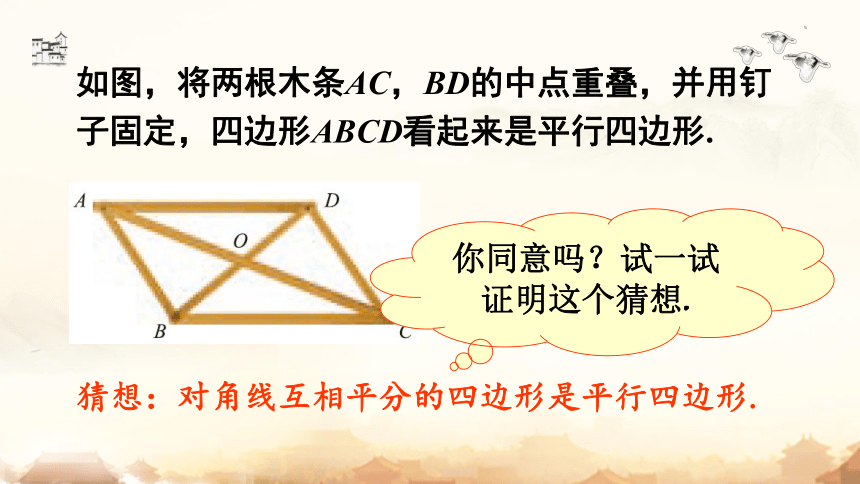
如图,将两根木条AC,BD的中点重叠,并用钉子固定,四边形ABCD看起来是平行四边形.
你同意吗?试一试证明这个猜想.
猜想:对角线互相平分的四边形是平行四边形.
第叁章节
新知探究
新知探究
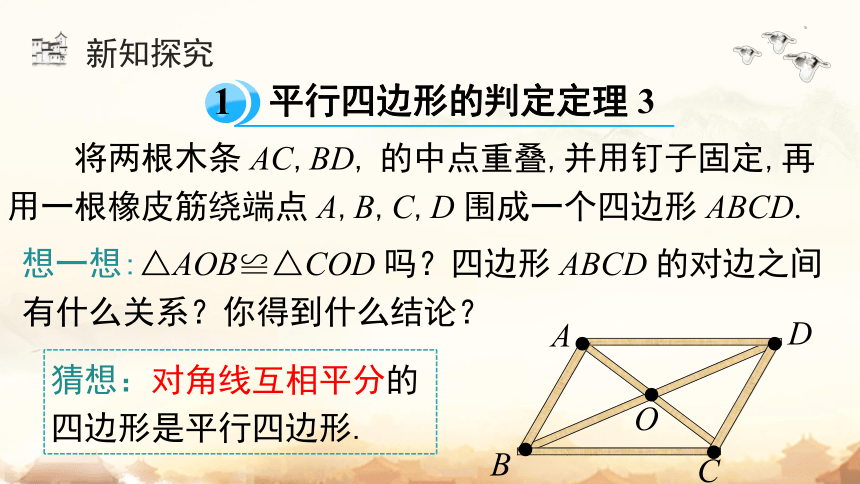
将两根木条 AC,BD, 的中点重叠,并用钉子固定,再用一根橡皮筋绕端点 A,B,C,D 围成一个四边形 ABCD.
猜想:对角线互相平分的四边形是平行四边形.
1
平行四边形的判定定理 3
A
B
C
D
O
想一想:△AOB≌△COD 吗?四边形 ABCD 的对边之间有什么关系?你得到什么结论?
已知:四边形 ABCD 的两条对角线,AC 与 BD
相交于点 O ,并且 OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
证明:∵ OA = OC,OB = OD ,
∠AOB =∠COD ,
∴△AOD≌△COB.
∴AD = CB,∠ADO =∠CBO.
∴ AD∥CB.
∴ 四边形 ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).
对角线互相平分的四边形是平行四边形.
∵ AO = CO,
BO = DO,
∴ 四边形 ABCD 是平行四边形.
几何语言:
A
B
C
D
O
总结归纳
平行四边形判定定理3
例1 已知:E,F 是平行四边形 ABCD 对角线 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
O
B
A
C
E
F
D
证明:连接 BD 交 AC 于点 O.
∵四边形ABCD 是平行四边形,
∴AO = CO,BO = DO
(平行四边形对角线互相平分).
典例精析
∴ AO - AE = CO - CF,即 EO = FO.
∴ 四边形 BFDE 是平行四边形.(对角线互相平分的四边形是平行四边形)
∵ AE = CF,
O
B
A
C
E
F
D
1. 如图,四边形 ABCD 的对角线交于点 O,下列哪组条件不能判断四边形 ABCD 是平行四边形( )
A.OA = OC,OB = OD
B.AB = CD,AO = CO
C.AB = CD,AD = BC
D.∠BAD =∠BCD,AB∥CD
B
O
D
A
C
B
练一练
2. 如图,AB、CD 相交于点 O,AC∥DB,AO=BO,E、F 分别是 OC、OD 的中点.
求证: 四边形 AFBE 是平行四边形.
证明: ∵AC∥BD,∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD (AAS).
∴ CO=DO.
∵ E、F 分别是 OC、OD 的中点,
∴ EO=FO. 又∵AO=BO,
∴ 四边形 AFBE 是平行四边形.
走进生活
3. 昨天小明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想买一块玻璃赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来 然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢( A,B,C 为三顶点,即找出第四个顶点 D )?
A
B
C
D
A
B
C
方法一依据:两组对边分别平行的四边形是平行四边形.
方法一:
D
A
B
C
方法二依据:两组对边分别相等的四边形是平行四边形.
方法二:
D
O
A
B
C
方法三依据:对角线互相平分的四边形是平行四边形.
方法三:
第肆章节
随堂练习
随堂练习
1.如图,四边形的对角线,交于点,过点 ,若
, ,则图中全等的三角形有___对.
6
(第1题)
2.如图,,是相交的两条线段,分别为它们的中点.当绕点 旋
转时(不与重合),连接,,,所得到的四边形 始终为
__________形.
平行四边
(第2题)
3.已知平行四边形的周长为 ,一条对角线把它分成两个三角形,周
长都是 ,则这条对角线长是______.
4.如图,在四边形中,,交于点,且, ,
,则____ .
70
5.如图,在中,,点,, 分别在边
,,上,,,则四边形 的
周长是( ).
B
A.8 B.16 C.24 D.32
6.在四边形中,对角线, 交于点
,若, ,
, ,求证:四边形
为平行四边形.
证明:,, ,
.
,,且 ,
四边形 为平行四边形.
7.如图,在平行四边形中,, 为对
角线上两点,且满足 ,连接
,,,.求证:四边形 为平行
四边形.
证明:如图,连接交于点 .
四边形 是平行四边形,
,
.
, ,
,, .
四边形 为平行四边形.
8.如图,在四边形中,, .试判断:
解:, ,
四边形 为平行四边形.
(1)图中哪些边可以通过平移而相互重合?
[答案] 平移的线段应是平行的,那么只有平行四边形的两组对边可通过
平移得到,故通过平移得到的有与,与 .
(2)图中哪些三角形可以通过旋转而相互重合?
[答案] 平行四边形是中心对称图形,绕对角线的交点旋转 后可与
原图形重合.
那么图中所有的全等三角形都可以通过旋转得到,即与 ,
与,与,与 .
9.如图,在中,,是对角线 的三等分点.求证:四边形
是平行四边形.
证明:,是对角线 的三等分点,且四边形 是平行四边形,
,且, ,
.
在和中,
,,同理可证 ,
四边形 是平行四边形.
10.小刚做好了一个四边形木框,他想知道这个木框是否为平行四边形木
框,他手头仅有一把刻度尺,请你为他想想办法,你能想到几种方法
解:根据两组对边分别相等的四边形是平行四边形或对角线互相平分的四
边形是平行四边形,利用刻度尺量取两组对边是否相等或利用刻度尺量
取两对角线是否互相平分.
11.如图,已知在四边形中,,对角线,相交于点 ,
且是 的中点.
(1)求证: ;
证明: ,
, .
是的中点, .
在和中,
.
(2)求证:四边形 是平行四边形.
[答案] 由(1)知 ,
.又 ,
四边形 是平行四边形.
12.如图,的对角线,相交于点 ,且
,,,分别是,,, 的中点.求证:四边
形 是平行四边形.
证明: 四边形 是平行四边形,
, .
,,,分别是,,,的中点,, ,
,,, ,
四边形 是平行四边形.
13.综合实践课上,老师让同学们开展了的折纸活动,是 边
上的一动点,是边上的一动点,将沿直线折叠,使点
落在边上的点处,点的对应点为点,连接 .
(1)【观察发现】如图1,若 ,, ,
求 的长;
图1
图1
解:由折叠知 ,
,
.
, , .
由勾股定理得
, ,
,
, .
图1
(2)【操作探究】如图2,当点落在 的延长线上时,求证:四边形
为平行四边形.
图2
图2
证明:由折叠知, .
由得, ,
.
, .
.
.
图2
,,点在 的延长线上,
.
.
, .
又 ,
四边形 是平行四边形.
第伍章节
课堂小结
课堂小结
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形 (判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学八年级下册
第六章 平行四边形
汇报人:孙老师
汇报班级:X级X班
6.2 第2课时 利用四边形对角线的性质判定
2 平行四边形的判定
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
课前复习
如图,,要使四边形 成为平行四边形,还需要补充下列
条件中的( ).
C
A. B.
C. D.
第贰章节
新课导入
新课导入
前面我们已经知道:
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
你还能找到其他的判定方法吗?
如图,将两根木条AC,BD的中点重叠,并用钉子固定,四边形ABCD看起来是平行四边形.
你同意吗?试一试证明这个猜想.
猜想:对角线互相平分的四边形是平行四边形.
第叁章节
新知探究
新知探究
将两根木条 AC,BD, 的中点重叠,并用钉子固定,再用一根橡皮筋绕端点 A,B,C,D 围成一个四边形 ABCD.
猜想:对角线互相平分的四边形是平行四边形.
1
平行四边形的判定定理 3
A
B
C
D
O
想一想:△AOB≌△COD 吗?四边形 ABCD 的对边之间有什么关系?你得到什么结论?
已知:四边形 ABCD 的两条对角线,AC 与 BD
相交于点 O ,并且 OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
证明:∵ OA = OC,OB = OD ,
∠AOB =∠COD ,
∴△AOD≌△COB.
∴AD = CB,∠ADO =∠CBO.
∴ AD∥CB.
∴ 四边形 ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).
对角线互相平分的四边形是平行四边形.
∵ AO = CO,
BO = DO,
∴ 四边形 ABCD 是平行四边形.
几何语言:
A
B
C
D
O
总结归纳
平行四边形判定定理3
例1 已知:E,F 是平行四边形 ABCD 对角线 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
O
B
A
C
E
F
D
证明:连接 BD 交 AC 于点 O.
∵四边形ABCD 是平行四边形,
∴AO = CO,BO = DO
(平行四边形对角线互相平分).
典例精析
∴ AO - AE = CO - CF,即 EO = FO.
∴ 四边形 BFDE 是平行四边形.(对角线互相平分的四边形是平行四边形)
∵ AE = CF,
O
B
A
C
E
F
D
1. 如图,四边形 ABCD 的对角线交于点 O,下列哪组条件不能判断四边形 ABCD 是平行四边形( )
A.OA = OC,OB = OD
B.AB = CD,AO = CO
C.AB = CD,AD = BC
D.∠BAD =∠BCD,AB∥CD
B
O
D
A
C
B
练一练
2. 如图,AB、CD 相交于点 O,AC∥DB,AO=BO,E、F 分别是 OC、OD 的中点.
求证: 四边形 AFBE 是平行四边形.
证明: ∵AC∥BD,∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD (AAS).
∴ CO=DO.
∵ E、F 分别是 OC、OD 的中点,
∴ EO=FO. 又∵AO=BO,
∴ 四边形 AFBE 是平行四边形.
走进生活
3. 昨天小明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想买一块玻璃赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来 然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢( A,B,C 为三顶点,即找出第四个顶点 D )?
A
B
C
D
A
B
C
方法一依据:两组对边分别平行的四边形是平行四边形.
方法一:
D
A
B
C
方法二依据:两组对边分别相等的四边形是平行四边形.
方法二:
D
O
A
B
C
方法三依据:对角线互相平分的四边形是平行四边形.
方法三:
第肆章节
随堂练习
随堂练习
1.如图,四边形的对角线,交于点,过点 ,若
, ,则图中全等的三角形有___对.
6
(第1题)
2.如图,,是相交的两条线段,分别为它们的中点.当绕点 旋
转时(不与重合),连接,,,所得到的四边形 始终为
__________形.
平行四边
(第2题)
3.已知平行四边形的周长为 ,一条对角线把它分成两个三角形,周
长都是 ,则这条对角线长是______.
4.如图,在四边形中,,交于点,且, ,
,则____ .
70
5.如图,在中,,点,, 分别在边
,,上,,,则四边形 的
周长是( ).
B
A.8 B.16 C.24 D.32
6.在四边形中,对角线, 交于点
,若, ,
, ,求证:四边形
为平行四边形.
证明:,, ,
.
,,且 ,
四边形 为平行四边形.
7.如图,在平行四边形中,, 为对
角线上两点,且满足 ,连接
,,,.求证:四边形 为平行
四边形.
证明:如图,连接交于点 .
四边形 是平行四边形,
,
.
, ,
,, .
四边形 为平行四边形.
8.如图,在四边形中,, .试判断:
解:, ,
四边形 为平行四边形.
(1)图中哪些边可以通过平移而相互重合?
[答案] 平移的线段应是平行的,那么只有平行四边形的两组对边可通过
平移得到,故通过平移得到的有与,与 .
(2)图中哪些三角形可以通过旋转而相互重合?
[答案] 平行四边形是中心对称图形,绕对角线的交点旋转 后可与
原图形重合.
那么图中所有的全等三角形都可以通过旋转得到,即与 ,
与,与,与 .
9.如图,在中,,是对角线 的三等分点.求证:四边形
是平行四边形.
证明:,是对角线 的三等分点,且四边形 是平行四边形,
,且, ,
.
在和中,
,,同理可证 ,
四边形 是平行四边形.
10.小刚做好了一个四边形木框,他想知道这个木框是否为平行四边形木
框,他手头仅有一把刻度尺,请你为他想想办法,你能想到几种方法
解:根据两组对边分别相等的四边形是平行四边形或对角线互相平分的四
边形是平行四边形,利用刻度尺量取两组对边是否相等或利用刻度尺量
取两对角线是否互相平分.
11.如图,已知在四边形中,,对角线,相交于点 ,
且是 的中点.
(1)求证: ;
证明: ,
, .
是的中点, .
在和中,
.
(2)求证:四边形 是平行四边形.
[答案] 由(1)知 ,
.又 ,
四边形 是平行四边形.
12.如图,的对角线,相交于点 ,且
,,,分别是,,, 的中点.求证:四边
形 是平行四边形.
证明: 四边形 是平行四边形,
, .
,,,分别是,,,的中点,, ,
,,, ,
四边形 是平行四边形.
13.综合实践课上,老师让同学们开展了的折纸活动,是 边
上的一动点,是边上的一动点,将沿直线折叠,使点
落在边上的点处,点的对应点为点,连接 .
(1)【观察发现】如图1,若 ,, ,
求 的长;
图1
图1
解:由折叠知 ,
,
.
, , .
由勾股定理得
, ,
,
, .
图1
(2)【操作探究】如图2,当点落在 的延长线上时,求证:四边形
为平行四边形.
图2
图2
证明:由折叠知, .
由得, ,
.
, .
.
.
图2
,,点在 的延长线上,
.
.
, .
又 ,
四边形 是平行四边形.
第伍章节
课堂小结
课堂小结
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形 (判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
两组对角分别相等的四边形是平行四边形(定义拓展)
对角线互相平分的四边形是平行四边形(判定定理3)
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
