6.2 第1课时 利用四边形边的关系判定平行四边形 课件(共34张PPT)
文档属性
| 名称 | 6.2 第1课时 利用四边形边的关系判定平行四边形 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
北师大版数学八年级下册
第六章 平行四边形
汇报人:孙老师
汇报班级:X级X班
6.2 第1课时 利用四边形边的关系判定平行四边形
2 平行四边形的判定
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
课前复习
如图,四边形 是平行四边形,以下四个结论中:
; ; ;
.
正确的有( ).
B
A.①②③ B.①③④ C.①②④ D.②③④
第贰章节
新课导入
新课导入
1.什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
2.我们学行四边形的哪些性质?
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
边
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC .
角
∵四边形ABCD是平行四边形 ∴∠A=∠C,∠D=∠B .
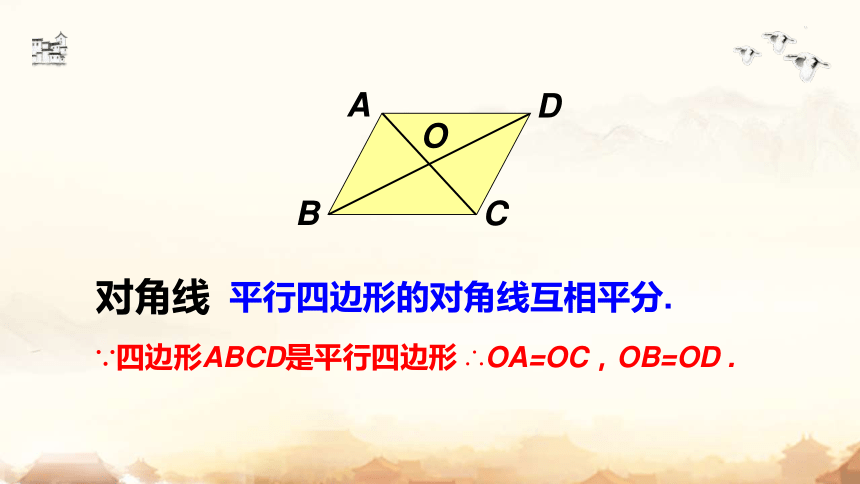
平行四边形的对角线互相平分.
对角线
∵四边形ABCD是平行四边形 ∴OA=OC,OB=OD .
A
B
C
D
O
第叁章节
新知探究
新知探究
活动:用两根长 30 cm 的木条和两根长 20 cm 的木条作为四边形的四条边,能否拼成一个平行四边形?
20 cm
30 cm
猜测:两组对边分别相等的四边形是平行四边形.
1
平行四边形的判定定理 1
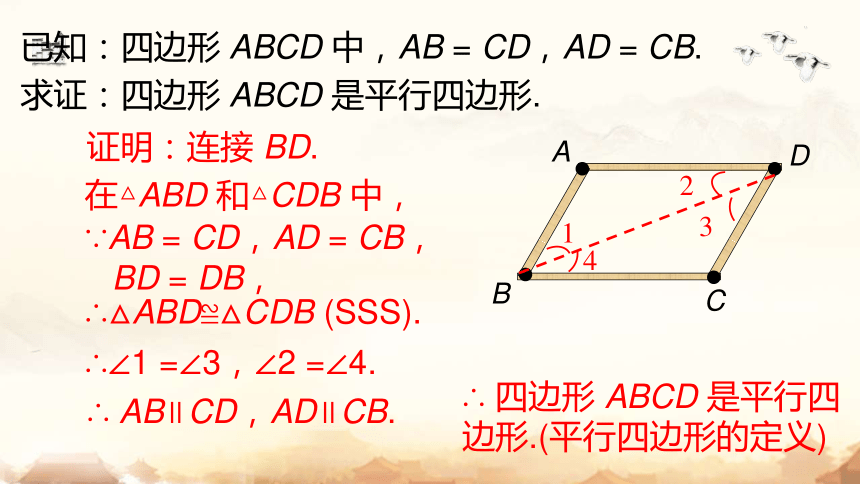
已知:四边形 ABCD 中,AB = CD,AD = CB.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
证明:连接 BD.
在△ABD 和△CDB 中,
∵AB = CD,AD = CB,
BD = DB,
∴△ABD≌△CDB (SSS).
∴∠1 =∠3,∠2 =∠4.
∴ AB∥CD,AD∥CB.
∴ 四边形 ABCD 是平行四边形.(平行四边形的定义)
1
4
2
3
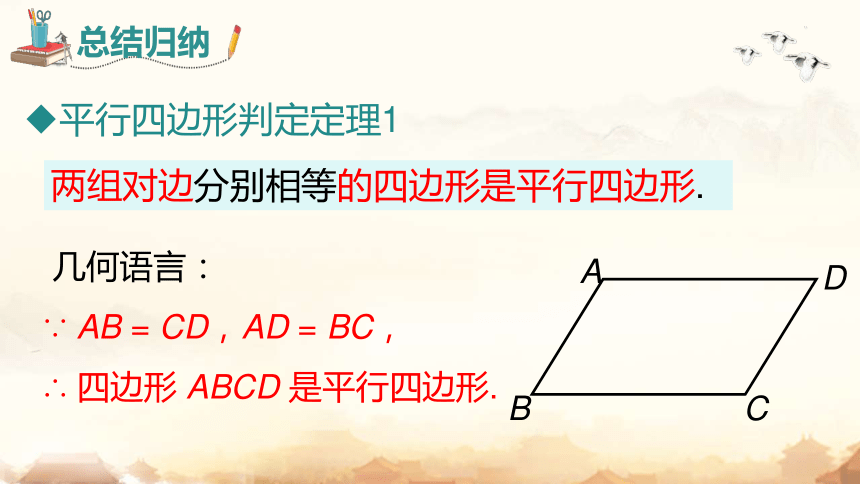
两组对边分别相等的四边形是平行四边形.
∵ AB = CD,
AD = BC,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
练一练
证明:在 Rt△ABC 和 Rt△ADC 中,
AC = CA,
AB = CD,
∴ Rt△ABC≌Rt△CDA(HL).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
1. 如图,AD⊥AC,BC⊥AC,且 AB = CD.
求证:四边形 ABCD 是平行四边形.
(1) 取两根长度相等的细木条,你能将它们摆放在一张纸上,使得这两跟细木条的四个端点恰好是一个平行四边形的四个顶点吗
2
平行四边形的判定定理 2
A
B
C
D
B
C
A
D
议一议
猜想:一组对边平行且相等的四边形是平行四边形.
(2) 如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形
B
D
C
A
证明:连接 AC.
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD,且AB = CD.
求证:四边形 ABCD 是平行四边形.
1
2
∵ AB//CD, ∴∠1 = ∠2.
又∵ AB = CD,AC = CA,
∴△ABC≌△CDA. ∴ BC = DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形.
∵ AB = CD,
AB∥CD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例1 如图,在平行四边形 ABCD 中,已知 E、F
分别是 AD、CB 的中点.
求证:四边形 BFDE 是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ ED = AD, FB = CB. ∴ ED = FB ,ED∥FB .
B
A
C
D
E
F
∴AD = CB(平行四边形对边相等),
AD∥CB(平行四边形定义).
∵E、F 分别是 AD、CB 的中点
∴ 四边形 BFDE 是平行四边形 (一组对边平行且相等的四边形是平行四边形).
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框?为什么?
7 cm
4 cm
3 cm
3 cm
5 cm
4 cm
拓展思考
4 cm
4 cm
4 cm
4 cm
3 cm
3 cm
3 cm
3 cm
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形. 两组边相等四边形也不一定是平行四边形.
3 cm
4 cm
4 cm
7 cm
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
3
由定义判定平行四边形
已知:四边形 ABCD 中,∠A =∠C,∠B =∠D.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
又∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴ 四边形 ABCD 是平行四边形.
同理得 AB∥CD.
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,∴四边形ABCD是
ABCD
A
B
C
D
∵AB=CD,AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是
ABCD
总结归纳
第肆章节
随堂练习
随堂练习
1.在中,, ,则下列结论中正确的是( ).
D
A. B.
C. D.
2.下列条件中,不能判定四边形是平行四边形的是( ).
B
A.两组对边分别平行 B.一组对边平行,另一组对边相等
C.两组对边分别相等 D.一组对边平行且相等
3.下列条件中,能判定四边形是平行四边形的是( ).
C
A.一组对边相等,另一组对边平行 B.一组对边平行,一组邻角相等
C.一组对角相等,一组邻角互补 D.一组对角互补,另一组对角相等
4.依据所标角度和边长的数据,下列四边形一定为平行四边形的是
( ).
A
A. B. C. D.
5.如图,四边形 ____(选填“是”或“不是”)平行四边形,理由是
_______________________________________.
是
两组对边分别相等的四边形是平行四边形
6.如图,当____时,四边形 是平行四边形.
14
(第6题)
7.已知四边形中,,要使四边形 为平行四边形,需添
加一个条件是_____________________.(只需填一个你认为正确的条件即可)
(答案不唯一)
8.如图,在中,,是的三等分点,,是 的三等分点,
则图中的平行四边形共有___个.
6
(第8题)
9.如图,在平行四边形中,, 分别是边
,上的一点,且,连接, .
求证:四边形 是平行四边形.
证明: 四边形 是平行四边形,
, .
又,, ,
四边形 是平行四边形.
第伍章节
课堂小结
课堂小结
平行四边形的判定
定义法
判定理理1
判定定理2
①已知一组对边平行,可以证另一组对边平行;也可证这组对边相等.
②已知一组对边相等,可以证另一组对边相等;也可证这组对边平行.
③已知一组对角相等,再证另一组对角相等.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学八年级下册
第六章 平行四边形
汇报人:孙老师
汇报班级:X级X班
6.2 第1课时 利用四边形边的关系判定平行四边形
2 平行四边形的判定
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
课前复习
如图,四边形 是平行四边形,以下四个结论中:
; ; ;
.
正确的有( ).
B
A.①②③ B.①③④ C.①②④ D.②③④
第贰章节
新课导入
新课导入
1.什么是平行四边形?
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
2.我们学行四边形的哪些性质?
平行四边形的两组对边分别相等;
平行四边形的两组对角分别相等;
边
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC .
角
∵四边形ABCD是平行四边形 ∴∠A=∠C,∠D=∠B .
平行四边形的对角线互相平分.
对角线
∵四边形ABCD是平行四边形 ∴OA=OC,OB=OD .
A
B
C
D
O
第叁章节
新知探究
新知探究
活动:用两根长 30 cm 的木条和两根长 20 cm 的木条作为四边形的四条边,能否拼成一个平行四边形?
20 cm
30 cm
猜测:两组对边分别相等的四边形是平行四边形.
1
平行四边形的判定定理 1
已知:四边形 ABCD 中,AB = CD,AD = CB.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
证明:连接 BD.
在△ABD 和△CDB 中,
∵AB = CD,AD = CB,
BD = DB,
∴△ABD≌△CDB (SSS).
∴∠1 =∠3,∠2 =∠4.
∴ AB∥CD,AD∥CB.
∴ 四边形 ABCD 是平行四边形.(平行四边形的定义)
1
4
2
3
两组对边分别相等的四边形是平行四边形.
∵ AB = CD,
AD = BC,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理1
B
D
C
A
总结归纳
练一练
证明:在 Rt△ABC 和 Rt△ADC 中,
AC = CA,
AB = CD,
∴ Rt△ABC≌Rt△CDA(HL).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
1. 如图,AD⊥AC,BC⊥AC,且 AB = CD.
求证:四边形 ABCD 是平行四边形.
(1) 取两根长度相等的细木条,你能将它们摆放在一张纸上,使得这两跟细木条的四个端点恰好是一个平行四边形的四个顶点吗
2
平行四边形的判定定理 2
A
B
C
D
B
C
A
D
议一议
猜想:一组对边平行且相等的四边形是平行四边形.
(2) 如果四边形有一组对边相等,那么还需要添加什么条件,才能使它成为平行四边形
B
D
C
A
证明:连接 AC.
D
A
B
C
已知:如图,在四边形ABCD中,AB//CD,且AB = CD.
求证:四边形 ABCD 是平行四边形.
1
2
∵ AB//CD, ∴∠1 = ∠2.
又∵ AB = CD,AC = CA,
∴△ABC≌△CDA. ∴ BC = DA.
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
一组对边平行且相等的四边形是平行四边形.
∵ AB = CD,
AB∥CD,
∴ 四边形 ABCD 是平行四边形.
几何语言:
平行四边形判定定理2
B
D
C
A
总结归纳
例1 如图,在平行四边形 ABCD 中,已知 E、F
分别是 AD、CB 的中点.
求证:四边形 BFDE 是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ ED = AD, FB = CB. ∴ ED = FB ,ED∥FB .
B
A
C
D
E
F
∴AD = CB(平行四边形对边相等),
AD∥CB(平行四边形定义).
∵E、F 分别是 AD、CB 的中点
∴ 四边形 BFDE 是平行四边形 (一组对边平行且相等的四边形是平行四边形).
卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框?为什么?
7 cm
4 cm
3 cm
3 cm
5 cm
4 cm
拓展思考
4 cm
4 cm
4 cm
4 cm
3 cm
3 cm
3 cm
3 cm
发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形. 两组边相等四边形也不一定是平行四边形.
3 cm
4 cm
4 cm
7 cm
思考:我们可以从角出发来判定一个四边形是否为平行四边形吗?
A
B
C
D
你能根据平行四边形的定义证明它们吗?
3
由定义判定平行四边形
已知:四边形 ABCD 中,∠A =∠C,∠B =∠D.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
又∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴ 四边形 ABCD 是平行四边形.
同理得 AB∥CD.
证明:
定义判定:
两组对角分别相等的四边形是平行四边形
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,∴四边形ABCD是
ABCD
A
B
C
D
∵AB=CD,AB∥CD,
∴四边形ABCD是
ABCD
A
B
C
D
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是
ABCD
总结归纳
第肆章节
随堂练习
随堂练习
1.在中,, ,则下列结论中正确的是( ).
D
A. B.
C. D.
2.下列条件中,不能判定四边形是平行四边形的是( ).
B
A.两组对边分别平行 B.一组对边平行,另一组对边相等
C.两组对边分别相等 D.一组对边平行且相等
3.下列条件中,能判定四边形是平行四边形的是( ).
C
A.一组对边相等,另一组对边平行 B.一组对边平行,一组邻角相等
C.一组对角相等,一组邻角互补 D.一组对角互补,另一组对角相等
4.依据所标角度和边长的数据,下列四边形一定为平行四边形的是
( ).
A
A. B. C. D.
5.如图,四边形 ____(选填“是”或“不是”)平行四边形,理由是
_______________________________________.
是
两组对边分别相等的四边形是平行四边形
6.如图,当____时,四边形 是平行四边形.
14
(第6题)
7.已知四边形中,,要使四边形 为平行四边形,需添
加一个条件是_____________________.(只需填一个你认为正确的条件即可)
(答案不唯一)
8.如图,在中,,是的三等分点,,是 的三等分点,
则图中的平行四边形共有___个.
6
(第8题)
9.如图,在平行四边形中,, 分别是边
,上的一点,且,连接, .
求证:四边形 是平行四边形.
证明: 四边形 是平行四边形,
, .
又,, ,
四边形 是平行四边形.
第伍章节
课堂小结
课堂小结
平行四边形的判定
定义法
判定理理1
判定定理2
①已知一组对边平行,可以证另一组对边平行;也可证这组对边相等.
②已知一组对边相等,可以证另一组对边相等;也可证这组对边平行.
③已知一组对角相等,再证另一组对角相等.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
