2024-2025学年八年级下学期数学期考末模拟卷(浙江杭州市专用) 【答案+解析】
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末模拟卷(浙江杭州市专用) 【答案+解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 424.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:03:33 | ||
图片预览




文档简介
保密★启用前
2024-2025学年八年级下册期末模拟卷(杭州市专用)
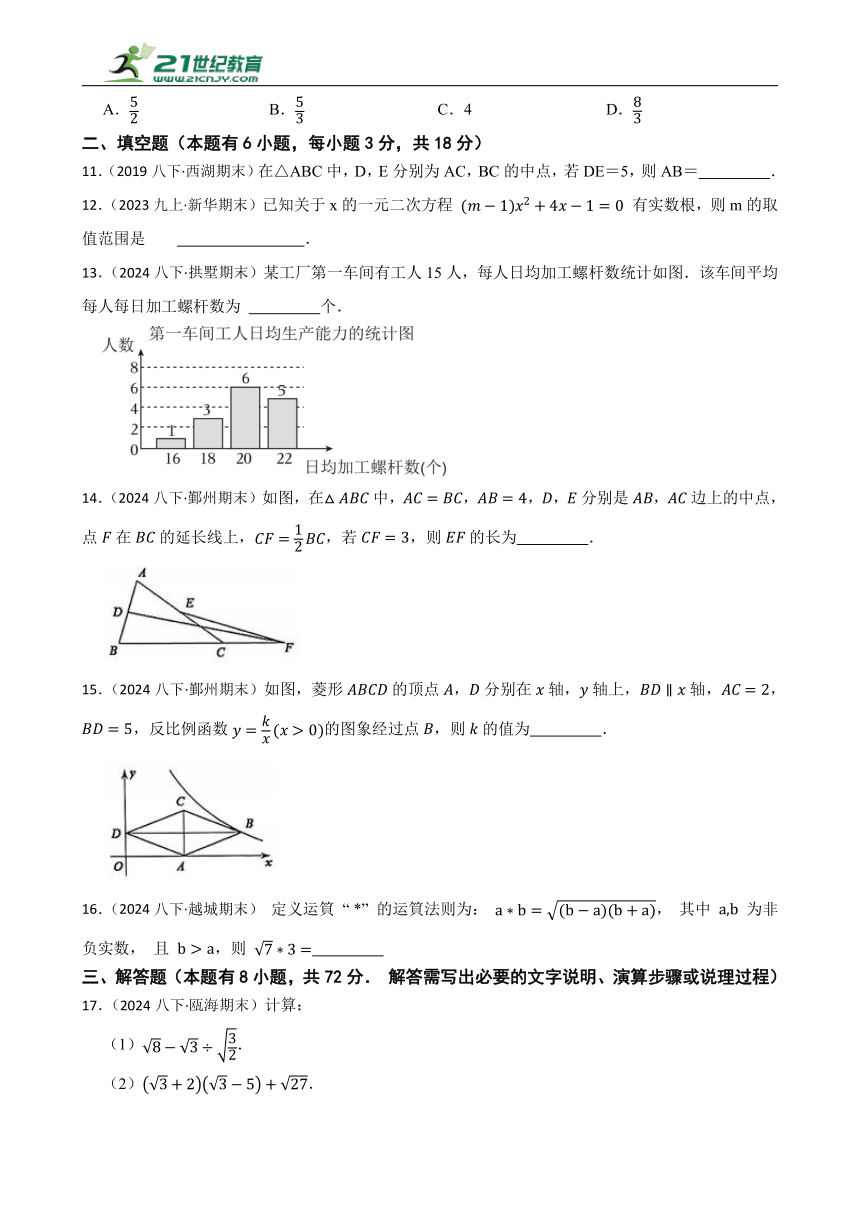
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.(2024八下·奉化期末)下列图形是我国国产品牌汽车的标识,这些汽车标识中,既是轴对称图形又是中心对称图形的( )
A. B.
C. D.
2.(2023八下·江北期末)下列计算正确的是( )
A. B. C. D.
3.(2023八下·荆州期末)下列二次根式中,不能与合并的是( )
A. B. C. D.
4.(2024八下·浦江期末)用配方法解一元二次方程x2﹣4x﹣6=0时,配方后的方程是( )
A.(x+2)2=2 B.(x﹣2)2=2
C.(x+2)2=10 D.(x﹣2)2=10
5.(2024八下·金华期末)《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架,其中方程术是《九章算术》最高的数学成就.《九章算术》记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少(1丈=10尺,1尺=10寸)?设矩形门宽为x尺,则所列方程为( ).
A. B.
C. D.
6.(2024八下·滨江期末)某篮球队 5 名场上队员的身高 (单位: ) 分别是: . 现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,换人后场上队员的身高
A.平均数变小, 方差变小 B.平均数变小, 方差变大
C.平均数变大, 方差变小 D.平均数变大, 方差变大
7.(2025九上·丰顺期末)平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
8.(2024八下·三门期末)如图,在四边形中,点E,F,G,H分别是各边的中点.甲说:若四边形是平行四边形,则四边形也是平行四边形;乙说:若四边形是平行四边形,则四边形也是平行四边形.下列说法正确的是( )
A.甲、乙都正确 B.甲正确,乙错误
C.甲错误,乙正确 D.甲、乙都错误
9.(2024八下·温州期末)如图,在矩形中,,分别是边,上的点,且,将矩形沿折叠,点恰好落在边上点处,再将沿折叠,点恰好落在上的点处.若,,则的长为( )
A. B. C. D.
10.(2024八下·西湖期末)如图,过的图象上点,分别作轴,轴的平行线交的图象于,两点,以,为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为,,,,若,则的值为( )
A. B. C.4 D.
二、填空题(本题有6小题,每小题3分,共18分)
11.(2019八下·西湖期末)在△ABC中,D,E分别为AC,BC的中点,若DE=5,则AB= .
12.(2023九上·新华期末)已知关于x的一元二次方程 有实数根,则m的取值范围是 .
13.(2024八下·拱墅期末)某工厂第一车间有工人15人,每人日均加工螺杆数统计如图.该车间平均每人每日加工螺杆数为 个.
14.(2024八下·鄞州期末)如图,在中,,,,分别是,边上的中点,点在的延长线上,,若,则的长为 .
15.(2024八下·鄞州期末)如图,菱形的顶点,分别在轴,轴上,轴,,,反比例函数的图象经过点,则的值为 .
16.(2024八下·越城期末) 定义运筫 “ *” 的运筫法则为: , 其中 为非负实数, 且 ,则
三、解答题(本题有8小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.(2024八下·瓯海期末)计算:
(1).
(2).
18.(2024八下·义乌期末)解方程:
(1);
(2).
19.(2024八下·鄞州期末)小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别 平时 期中考试 期末考试
测验1 测验2 测验3 课题学习
成绩 88 70 96 86 85
(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
20.(2024八下·东阳期末)如图,在正方形网格中,每个小正方形的边长均为1.
(1)请在网格中画出一组邻边长为,的,使各顶点都在网格线的交点上;
(2)题(1)中的是矩形吗?答: .(填“是”或“不是”)
21.(2024八下·钱塘期末)已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+3=0.
(1)若该方程有一个根是﹣2,求k的值.
(2)若该方程有两个实数根,求k的取值范围.
(3)若该方程的两个实数根x1,x2满足(x1﹣1)(x2﹣1)=14,求k的值.
22.(2024八下·东阳期末)如图1,已知菱形,点E是对角线上任意一点(不与端点B、D重合),连结,,,.
(1)求证:.
(2)若,则的值.
(3)如图2,延长交于点F,若是等腰三角形,求的长.
23.(2024八下·温州期末)如图,一次函数的图象与反比例四数的图象相交于A(1,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)当一次函数的值大于反比例函数的值时,直接写出的取值范围.
(3)直线交轴于点,点是轴上的点,的面积等于的面积,求点的坐标.
24.(2024八下·义乌期末)如图1,正方形的边长为4,点在上(不与重合),点在上(不与重合)且满足,连接并交于点.
(1)请问:线段与满足怎样的数量关系和位置关系?请说明理由.
(2)如图2,连结,若点为的中点,求的周长.
(3)如图3,延长至点使,连结,.若,求的面积.
答案解析部分
1.A
解:既是轴对称图形又是中心对称图形,故A符合题意;
既不是轴对称图形也不是中心对称图形,故B不符合题意;
既不是轴对称图形也不是中心对称图形,故C不符合题意;
是中心对称图形,但不是轴对称图形,故D不符合题意;
故答案为:A.
根据轴对称图形和中心对称图形的概念,对各选项逐一分析,再作出判断.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
2.D
解:A、,错误;
B、,错误;
C、,错误;
D、,正确 .
故答案为:D .
根据二次根式的运算法则、算术平方根的定义逐项判断,解求出答案.
3.C
解:A、,能与合并,故A不符合题意;
B、,能与合并,故B不符合题意;
C、,不能与合并,故C符合题意;
D、,能与合并,故D不符合题意.
故答案为:C.
分别将各选项中的二次根式化简,再观察被开方数可得答案.
4.D
解:,
移项,得,
配方,得,
即,
故答案为:D.
此方程是一元二次方程的一般形式,且二次项的系数为1,利用配方法解方程的时候,首先将常数项移到方程的右边,方程的两边都加上一次项系数一半的平方“4”,左边利用完全平方公式分解因式,右边合并同类项即可.
5.A
解:设矩形门宽为x尺,由题意得,
故答案为:A
设矩形门宽为x尺,根据“它的高比宽多6尺8寸,它的对角线长1丈”结合题意即可列出一元二次方程,从而即可求解。
6.A
解: 当用一名身高为 的队员换下场上身高为 195cm 的队员,换人前后相比,队员的身高总和减小,但队员人数不变,故平均数变小;
原本最大值为195,换人后换成194,数据的波动变小,故方差变小.
故答案为:A.
根据平均数和方差的定义和意义即可得出答案.
一般地,对于n个数x1,x2,...,xn,我们把叫做这n个数的算术平均数( mean),简称平均数.
方差是各个数据与平均数差的平方的平均数,方差越小,数据波动就越小,越稳定.
7.A
解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选A.
平行四边形、矩形、菱形、正方形都是特殊的平行四边形,因而平行四边形的性质就是四个图形都具有的性质.
8.B
解:如图所示,连接,
∵在四边形中,点E,F,G,H分别是各边的中点,
∴,
∴,
∴四边形是平行四边形,
根据现有条件无法证明四边形ABCD是平行四边形,故甲说法正确,乙说法不正确,
故答案为:B.
由三角形的中位线平行于第三边,且等于第三边的一半可得,从而根据一组对边平行且相等的四边形是平行四边形可证明四边形EFGH是平行四边形,据此可判断甲说法正确;根据现有条件无法证明四边形ABCD是平行四边形,据此可得答案.
9.D
解: ∵四边形ABCD是矩形,AB=1,AD=2,
∴AD∥BC,∠A=90°,AE=2-ED,
∴∠AEB=∠GBE,
由折叠得HB=AB=1,EG=ED,HE=AE=2-ED,∠BHE=∠A=90°,∠AEB=∠GEB,
∴GH=EG-HE=ED-(2-ED)=2ED-2,∠BHG=90°,∠GBE=∠GEB,
∴BG=EG=ED,
∵HB2+GH2=BG2,
∴12+(2ED-2)2=ED2,
整理得(3ED-5)(ED-1)=0,
∴或ED=1(不符合题意,舍去).
故答案为:D.
根据矩形的对边平行且相等,四个角都是直角可得AD∥BC,∠A=90°,AE=2-ED,根据两直线平行,内错角相等得出∠AEB=∠GBE,根据折叠前后两图形的对应角相等,对应边相等得出HB=AB=1,EG=ED,HE=AE=2-ED,∠BHE=∠A=90°,∠AEB=∠GEB,即可得出GH=2ED-2,∠BHG=90°,∠GBE=∠GEB,根据等角对等边得出BG=EG=ED,根据直角三角形两直角边的平方和等于斜边的平方可求出DE的值,
10.D
解:依题意,设,则,,
∵点A在的图象上
则,
同理∵B,D两点在的图象上,
则
∵
∴,
又∵,
故,
∴,
故答案为:D.
设,根据矩形的对边相等和反比例函数上点的特征可得,,,根据反比例函数系数k的几何意义可得,,代入求出,即得出,即可求得.
11.10
解: ∵D,E分别为AC,BC的中点 ,
∴DE是△ABC的中位线,DE=AB,
则AB=2DE=10;
故答案为:D.
因为D,E分别为AC,BC的中点 ,则DE是△ABC的中位线,现知DE的长,由三角形中位线定理即可求出AB的长。
12.m≥-3且m≠1
解:∵一元二次方程(m-1)x2+4x-1=0有实数根,
∴Δ=b2﹣4ac≥0,即16+4(m-1)≥0,
解得:m≥-3,
又∵m-1≠0,
∴m≠1,
综上所述:m≥-3且m≠1.
根据一元二次方程根的情况得,Δ=b2﹣4ac≥0,即16+4(m-1)≥0,又m-1≠0,解之即可求得m的取值范围.
13.20
解:该车间工人日均生产螺杆数的平均数为(16×1+18×3+20×6+22×5)÷15=20(个),
故答案为:20.
利用加权平均数的计算方法列出算式求解即可.
14.
解:如图,记的中点为,连接,
∵分别是边上的中点,
∴,
∵,,
∴,,
∴,
∵,
∴,
由勾股定理得,,
故答案为:.
设BC的中点为G,连接EG,求出EG的长,由AC=BC,BC=2CF,可求CF的长,GF的长,利用角的和差关系可证,由勾股定理得计算求解即可.
15.5
解:设菱形的对角线,相交于点E,
则,,
轴,
轴,
,
把代入,得,
.
故答案为:5.
设菱形ABCD的对角线AC,BD相交于点E,则根据菱形的性质可求出点B的坐标,代入反比例函数关系式求解,即得答案.
16.
解:
=
故答案为:.
根据公式:代入计算即可.
17.(1)解:
(2)解:
(1)先运算二次根式的除法、二次根式的化简,然后合并解题即可;
(2)先运算二次根式的乘法、二次根式的化简,再合并解题.
18.(1)解:,
方程左边分解因式,得,
所以或,
解得:,;
(2)解:,
方程左边分解因式,得,
所以或,
解得:,.
()利用提取公因式法分解因式,转化为两个一次方程求解;
()利用因式分解法,转化为两个一次方程求解.
(1)解:∵,
∴,
∴或,
∴,;
(2)解:∵,
∴,
∴或,
∴,.
19.解:(1)该学期的平时平均成绩为:(88+70+96+86)÷4=85(分).
(2)按照如图所示的权重,
依题意得:85×10%+85×30%+60% x≥90.
解得:x≥93.33,
又∵成绩均取整数,
∴x≥94.
答:期末考试成绩至少需要94分.
(1)平均数是指一组数据之和,除以这组数的个数,据此计算即可;
(2)将各数值乘以相应的权数,然后加总求和得到总和,再利用总和除以权重的总和即可得到该数组的加权平均数,据此结合“ 保证达到总评成绩90分的最低目标 ”列出不等式,求解即可.
20.(1)作图见解析
(2)不是
解:(1)如图,即为所求;
(2)
解:∵,,,
∴,
∴,
∴不是矩形,
故答案为:不是.
(1)根据勾股定理.再根据平行四边形的判定定理作图即可;
(2)根据勾股定理的逆定理,,,,所以不是矩形,
21.(1)解:x=2时,4﹣2(k﹣1)×(﹣2)+k2+3=0,
整理得k2+4k+3=0,
解得:k=﹣1或﹣3.
(2)解:根据题意得Δ=(2k﹣2)2﹣4k2>0,
解得k<1;
(3)解:根据题意得x1+x2=2k﹣2,x1x2=k2+3,
∵(x1﹣1)(x2﹣1)=14,
∴x1x2﹣(x1+x2)+1=14,
即k2+3﹣(2k﹣2)+1=14,
整理得k2﹣2k﹣8=0,解得k1=﹣2,k2=4,
∵k<1,
∴k=﹣2.
(1)把x=2时方程中可得关于k的方程,解之即可;
(2)由该方程有两个实数根,可得△>0,据此解答即可;
(3)利用根与系数的关系可得x1+x2=2k﹣2,x1x2=k2+3,再代入已知等式可得关于k的方程,解之即可.
22.(1)证明:四边形是菱形,
∴AB=CB,∠ABE=∠CBE,
∵BE=BE,
∴△ABE≌△CBE,
;
(2)解:连接AC交BD于点O,过点B作BF ∥AC交AE的延长线于点F,
由(1)知△ABE≌△CBE,
∴∠AEB=∠CEB,
∴∠AEO=∠CEO,
∴∠AEC=2∠AEO,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOE=90°,
∴∠AEO+∠EAO=90°,
∵,
∴2∠AEO+2∠BAE=180°,
∴∠AEO+∠BAE=90°,
∴∠BAE=∠EAO,
∵BF∥AC,
∴∠EFB=∠EAO,
∴∠BAE=∠EAO,
∴AB=BF,
∵BF∥AC,
∴△BEF∽△OEA,
∴,
∴,
在Rt△ABO中:∠AOB=90°,AB=5,BO=,
∴AO=4,
∴=,
∴,
∴,
又点O是AC和BD 的中点,
∴S△ABO=S菱形ABCD, ∴.
(3)①
在菱形,
,
,
,
,
连结交于点,
在中,
∵BF∥AD,
∴△BEF∽△DEA,
∴,
∴,
∴
②
在菱形,
,
,
过点E作的垂线交于点,过点E作的垂线交于点G,E,H,三点共线
由(2)所得,
,
延长过点A作的垂线交于点I,则四边形是矩形,
在中,,
,
,
,
,
,
设
③,不成立(舍去)
综上所述或
(1)根据菱形的性质得出AB=CB,∠ABE=∠CBE,从而利用SAS证得△ABE≌△CBE,从而得出;
(2)连接AC交BD于点O,过点B作BF ∥AC交AE的延长线于点F,首先证明∠BAE=∠EAO,然后再根据BF ∥AC,得出∠EFB=∠EAO,即可得出∠BAE=∠EAO,等角对等边得出AB=BF,再根据△BEF∽△OEA,得出,从而得出,再根据菱形的性质可得S△ABO=S菱形ABCD,即可得出。
(3)因为△CDE是等腰三角形,可分三种情况讨论:①,根据菱形的性质,可得DC=DE=AD=5,即可得出BE=BF=1,根据勾股定理可得AE=,然后根据△BEF∽△DEA,可得出,即可得出EF的长度;②,
在菱形中,,过点E作的垂线交于点,过点E作的垂线交于点G,E,H,三点共线,由(2)所得,;延长过点A作的垂线交于点I,则四边形是矩形,;在中,,;,;设,,③,,不成立(舍去);综上所述或。
23.(1)解:将A(1,3)代入反比例解析式得:,
,
∴反比例解析式为,
将B(-3,n)代入反比例解析式得:,
∴,
∴B(-3,-1),
将A(1,3)与B(-3,-1)代入中,得:
,
解得:,
∴一次函数解析式为;
(2)解:观察图象可得:一次函数值大于反比例函数值的的取值范围为或;
(3)解:∵点C为一次函数与x轴的交点坐标,
令,可得
∴,
即,
∴.
,
,
∵点是轴上的点,
∴设点P(a,0),
∴,
∴,.
∴或.
(1)将点A和点B坐标代入反比例解析式即可求出反比例函数解析式和点B坐标,再将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)一次函数的值大于反比例函数的值,一次函数的图象在反比例函数的图象上方,结合交点坐标,即可得到答案.
(3)先求出点C的坐标,根据面积相等求出PC的长度,进一步求出P点坐标.
(1)解:将A(1,3)代入反比例解析式得:,
,
∴反比例解析式为,
将B(-3,n)代入反比例解析式得:,
∴,
∴B(-3,-1),
将A(1,3)与B(-3,-1)代入中,得:,
解得:,
∴一次函数解析式为;
(2)解:由图象得:一次函数值大于反比例函数值的的取值范围为或;
(3)解:对于一次函数,令,得到,即C(-2,0),
∴.
∵的面积等于的面积,
,
,
∵点是轴上的点,
∴设点P(a,0),
∵C(-2,0),
∴,
解得,.
∴或.
24.(1)解:线段与的数量关系是、位置关系是,
理由如下:
∵四边形是正方形,
∴,,
在和中,
,
,,
,
,则;
(2)解:过点作,如图所示:
正方形的边长为4,
,且,
由(1)知,
在中,,,
点为的中点,
,
∴,
∵在中,,
∴,
∵在中,,,
∴,
∵在中,,
∴,
,
∵在中,,,
∴,
,
∵在中,,,
∴,
,
,
,,
,
的周长为;
(3)解:连接,过作,如图所示:
,,
是线段的垂直平分线,则,
,即是等腰三角形,
,则由勾股定理可得,
过点作,延长,过作于,如图:
∵在中,,
∴,
∵在中,,,
∴,
,
;,
.
2024-2025学年八年级下册期末模拟卷(杭州市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.(2024八下·奉化期末)下列图形是我国国产品牌汽车的标识,这些汽车标识中,既是轴对称图形又是中心对称图形的( )
A. B.
C. D.
2.(2023八下·江北期末)下列计算正确的是( )
A. B. C. D.
3.(2023八下·荆州期末)下列二次根式中,不能与合并的是( )
A. B. C. D.
4.(2024八下·浦江期末)用配方法解一元二次方程x2﹣4x﹣6=0时,配方后的方程是( )
A.(x+2)2=2 B.(x﹣2)2=2
C.(x+2)2=10 D.(x﹣2)2=10
5.(2024八下·金华期末)《九章算术》是我国传统数学中重要的著作之一,奠定了我国传统数学的基本框架,其中方程术是《九章算术》最高的数学成就.《九章算术》记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”大意:有一扇形状是矩形的门,它的高比宽多6尺8寸,它的对角线长1丈,问它的高与宽各是多少(1丈=10尺,1尺=10寸)?设矩形门宽为x尺,则所列方程为( ).
A. B.
C. D.
6.(2024八下·滨江期末)某篮球队 5 名场上队员的身高 (单位: ) 分别是: . 现用一名身高为 的队员换下场上身高为 的队员,与换人前相比,换人后场上队员的身高
A.平均数变小, 方差变小 B.平均数变小, 方差变大
C.平均数变大, 方差变小 D.平均数变大, 方差变大
7.(2025九上·丰顺期末)平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直平分且相等
8.(2024八下·三门期末)如图,在四边形中,点E,F,G,H分别是各边的中点.甲说:若四边形是平行四边形,则四边形也是平行四边形;乙说:若四边形是平行四边形,则四边形也是平行四边形.下列说法正确的是( )
A.甲、乙都正确 B.甲正确,乙错误
C.甲错误,乙正确 D.甲、乙都错误
9.(2024八下·温州期末)如图,在矩形中,,分别是边,上的点,且,将矩形沿折叠,点恰好落在边上点处,再将沿折叠,点恰好落在上的点处.若,,则的长为( )
A. B. C. D.
10.(2024八下·西湖期末)如图,过的图象上点,分别作轴,轴的平行线交的图象于,两点,以,为邻边的矩形被坐标轴分割成四个小矩形,面积分别记为,,,,若,则的值为( )
A. B. C.4 D.
二、填空题(本题有6小题,每小题3分,共18分)
11.(2019八下·西湖期末)在△ABC中,D,E分别为AC,BC的中点,若DE=5,则AB= .
12.(2023九上·新华期末)已知关于x的一元二次方程 有实数根,则m的取值范围是 .
13.(2024八下·拱墅期末)某工厂第一车间有工人15人,每人日均加工螺杆数统计如图.该车间平均每人每日加工螺杆数为 个.
14.(2024八下·鄞州期末)如图,在中,,,,分别是,边上的中点,点在的延长线上,,若,则的长为 .
15.(2024八下·鄞州期末)如图,菱形的顶点,分别在轴,轴上,轴,,,反比例函数的图象经过点,则的值为 .
16.(2024八下·越城期末) 定义运筫 “ *” 的运筫法则为: , 其中 为非负实数, 且 ,则
三、解答题(本题有8小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.(2024八下·瓯海期末)计算:
(1).
(2).
18.(2024八下·义乌期末)解方程:
(1);
(2).
19.(2024八下·鄞州期末)小青在本学期的数学成绩如下表所示(成绩均取整数):
测验类别 平时 期中考试 期末考试
测验1 测验2 测验3 课题学习
成绩 88 70 96 86 85
(1)计算小青本学期的平时平均成绩;
(2)如果学期的总评成绩是根据图所示的权重计算,那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标?
20.(2024八下·东阳期末)如图,在正方形网格中,每个小正方形的边长均为1.
(1)请在网格中画出一组邻边长为,的,使各顶点都在网格线的交点上;
(2)题(1)中的是矩形吗?答: .(填“是”或“不是”)
21.(2024八下·钱塘期末)已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+3=0.
(1)若该方程有一个根是﹣2,求k的值.
(2)若该方程有两个实数根,求k的取值范围.
(3)若该方程的两个实数根x1,x2满足(x1﹣1)(x2﹣1)=14,求k的值.
22.(2024八下·东阳期末)如图1,已知菱形,点E是对角线上任意一点(不与端点B、D重合),连结,,,.
(1)求证:.
(2)若,则的值.
(3)如图2,延长交于点F,若是等腰三角形,求的长.
23.(2024八下·温州期末)如图,一次函数的图象与反比例四数的图象相交于A(1,3),B(-3,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)当一次函数的值大于反比例函数的值时,直接写出的取值范围.
(3)直线交轴于点,点是轴上的点,的面积等于的面积,求点的坐标.
24.(2024八下·义乌期末)如图1,正方形的边长为4,点在上(不与重合),点在上(不与重合)且满足,连接并交于点.
(1)请问:线段与满足怎样的数量关系和位置关系?请说明理由.
(2)如图2,连结,若点为的中点,求的周长.
(3)如图3,延长至点使,连结,.若,求的面积.
答案解析部分
1.A
解:既是轴对称图形又是中心对称图形,故A符合题意;
既不是轴对称图形也不是中心对称图形,故B不符合题意;
既不是轴对称图形也不是中心对称图形,故C不符合题意;
是中心对称图形,但不是轴对称图形,故D不符合题意;
故答案为:A.
根据轴对称图形和中心对称图形的概念,对各选项逐一分析,再作出判断.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形;如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
2.D
解:A、,错误;
B、,错误;
C、,错误;
D、,正确 .
故答案为:D .
根据二次根式的运算法则、算术平方根的定义逐项判断,解求出答案.
3.C
解:A、,能与合并,故A不符合题意;
B、,能与合并,故B不符合题意;
C、,不能与合并,故C符合题意;
D、,能与合并,故D不符合题意.
故答案为:C.
分别将各选项中的二次根式化简,再观察被开方数可得答案.
4.D
解:,
移项,得,
配方,得,
即,
故答案为:D.
此方程是一元二次方程的一般形式,且二次项的系数为1,利用配方法解方程的时候,首先将常数项移到方程的右边,方程的两边都加上一次项系数一半的平方“4”,左边利用完全平方公式分解因式,右边合并同类项即可.
5.A
解:设矩形门宽为x尺,由题意得,
故答案为:A
设矩形门宽为x尺,根据“它的高比宽多6尺8寸,它的对角线长1丈”结合题意即可列出一元二次方程,从而即可求解。
6.A
解: 当用一名身高为 的队员换下场上身高为 195cm 的队员,换人前后相比,队员的身高总和减小,但队员人数不变,故平均数变小;
原本最大值为195,换人后换成194,数据的波动变小,故方差变小.
故答案为:A.
根据平均数和方差的定义和意义即可得出答案.
一般地,对于n个数x1,x2,...,xn,我们把叫做这n个数的算术平均数( mean),简称平均数.
方差是各个数据与平均数差的平方的平均数,方差越小,数据波动就越小,越稳定.
7.A
解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选A.
平行四边形、矩形、菱形、正方形都是特殊的平行四边形,因而平行四边形的性质就是四个图形都具有的性质.
8.B
解:如图所示,连接,
∵在四边形中,点E,F,G,H分别是各边的中点,
∴,
∴,
∴四边形是平行四边形,
根据现有条件无法证明四边形ABCD是平行四边形,故甲说法正确,乙说法不正确,
故答案为:B.
由三角形的中位线平行于第三边,且等于第三边的一半可得,从而根据一组对边平行且相等的四边形是平行四边形可证明四边形EFGH是平行四边形,据此可判断甲说法正确;根据现有条件无法证明四边形ABCD是平行四边形,据此可得答案.
9.D
解: ∵四边形ABCD是矩形,AB=1,AD=2,
∴AD∥BC,∠A=90°,AE=2-ED,
∴∠AEB=∠GBE,
由折叠得HB=AB=1,EG=ED,HE=AE=2-ED,∠BHE=∠A=90°,∠AEB=∠GEB,
∴GH=EG-HE=ED-(2-ED)=2ED-2,∠BHG=90°,∠GBE=∠GEB,
∴BG=EG=ED,
∵HB2+GH2=BG2,
∴12+(2ED-2)2=ED2,
整理得(3ED-5)(ED-1)=0,
∴或ED=1(不符合题意,舍去).
故答案为:D.
根据矩形的对边平行且相等,四个角都是直角可得AD∥BC,∠A=90°,AE=2-ED,根据两直线平行,内错角相等得出∠AEB=∠GBE,根据折叠前后两图形的对应角相等,对应边相等得出HB=AB=1,EG=ED,HE=AE=2-ED,∠BHE=∠A=90°,∠AEB=∠GEB,即可得出GH=2ED-2,∠BHG=90°,∠GBE=∠GEB,根据等角对等边得出BG=EG=ED,根据直角三角形两直角边的平方和等于斜边的平方可求出DE的值,
10.D
解:依题意,设,则,,
∵点A在的图象上
则,
同理∵B,D两点在的图象上,
则
∵
∴,
又∵,
故,
∴,
故答案为:D.
设,根据矩形的对边相等和反比例函数上点的特征可得,,,根据反比例函数系数k的几何意义可得,,代入求出,即得出,即可求得.
11.10
解: ∵D,E分别为AC,BC的中点 ,
∴DE是△ABC的中位线,DE=AB,
则AB=2DE=10;
故答案为:D.
因为D,E分别为AC,BC的中点 ,则DE是△ABC的中位线,现知DE的长,由三角形中位线定理即可求出AB的长。
12.m≥-3且m≠1
解:∵一元二次方程(m-1)x2+4x-1=0有实数根,
∴Δ=b2﹣4ac≥0,即16+4(m-1)≥0,
解得:m≥-3,
又∵m-1≠0,
∴m≠1,
综上所述:m≥-3且m≠1.
根据一元二次方程根的情况得,Δ=b2﹣4ac≥0,即16+4(m-1)≥0,又m-1≠0,解之即可求得m的取值范围.
13.20
解:该车间工人日均生产螺杆数的平均数为(16×1+18×3+20×6+22×5)÷15=20(个),
故答案为:20.
利用加权平均数的计算方法列出算式求解即可.
14.
解:如图,记的中点为,连接,
∵分别是边上的中点,
∴,
∵,,
∴,,
∴,
∵,
∴,
由勾股定理得,,
故答案为:.
设BC的中点为G,连接EG,求出EG的长,由AC=BC,BC=2CF,可求CF的长,GF的长,利用角的和差关系可证,由勾股定理得计算求解即可.
15.5
解:设菱形的对角线,相交于点E,
则,,
轴,
轴,
,
把代入,得,
.
故答案为:5.
设菱形ABCD的对角线AC,BD相交于点E,则根据菱形的性质可求出点B的坐标,代入反比例函数关系式求解,即得答案.
16.
解:
=
故答案为:.
根据公式:代入计算即可.
17.(1)解:
(2)解:
(1)先运算二次根式的除法、二次根式的化简,然后合并解题即可;
(2)先运算二次根式的乘法、二次根式的化简,再合并解题.
18.(1)解:,
方程左边分解因式,得,
所以或,
解得:,;
(2)解:,
方程左边分解因式,得,
所以或,
解得:,.
()利用提取公因式法分解因式,转化为两个一次方程求解;
()利用因式分解法,转化为两个一次方程求解.
(1)解:∵,
∴,
∴或,
∴,;
(2)解:∵,
∴,
∴或,
∴,.
19.解:(1)该学期的平时平均成绩为:(88+70+96+86)÷4=85(分).
(2)按照如图所示的权重,
依题意得:85×10%+85×30%+60% x≥90.
解得:x≥93.33,
又∵成绩均取整数,
∴x≥94.
答:期末考试成绩至少需要94分.
(1)平均数是指一组数据之和,除以这组数的个数,据此计算即可;
(2)将各数值乘以相应的权数,然后加总求和得到总和,再利用总和除以权重的总和即可得到该数组的加权平均数,据此结合“ 保证达到总评成绩90分的最低目标 ”列出不等式,求解即可.
20.(1)作图见解析
(2)不是
解:(1)如图,即为所求;
(2)
解:∵,,,
∴,
∴,
∴不是矩形,
故答案为:不是.
(1)根据勾股定理.再根据平行四边形的判定定理作图即可;
(2)根据勾股定理的逆定理,,,,所以不是矩形,
21.(1)解:x=2时,4﹣2(k﹣1)×(﹣2)+k2+3=0,
整理得k2+4k+3=0,
解得:k=﹣1或﹣3.
(2)解:根据题意得Δ=(2k﹣2)2﹣4k2>0,
解得k<1;
(3)解:根据题意得x1+x2=2k﹣2,x1x2=k2+3,
∵(x1﹣1)(x2﹣1)=14,
∴x1x2﹣(x1+x2)+1=14,
即k2+3﹣(2k﹣2)+1=14,
整理得k2﹣2k﹣8=0,解得k1=﹣2,k2=4,
∵k<1,
∴k=﹣2.
(1)把x=2时方程中可得关于k的方程,解之即可;
(2)由该方程有两个实数根,可得△>0,据此解答即可;
(3)利用根与系数的关系可得x1+x2=2k﹣2,x1x2=k2+3,再代入已知等式可得关于k的方程,解之即可.
22.(1)证明:四边形是菱形,
∴AB=CB,∠ABE=∠CBE,
∵BE=BE,
∴△ABE≌△CBE,
;
(2)解:连接AC交BD于点O,过点B作BF ∥AC交AE的延长线于点F,
由(1)知△ABE≌△CBE,
∴∠AEB=∠CEB,
∴∠AEO=∠CEO,
∴∠AEC=2∠AEO,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOE=90°,
∴∠AEO+∠EAO=90°,
∵,
∴2∠AEO+2∠BAE=180°,
∴∠AEO+∠BAE=90°,
∴∠BAE=∠EAO,
∵BF∥AC,
∴∠EFB=∠EAO,
∴∠BAE=∠EAO,
∴AB=BF,
∵BF∥AC,
∴△BEF∽△OEA,
∴,
∴,
在Rt△ABO中:∠AOB=90°,AB=5,BO=,
∴AO=4,
∴=,
∴,
∴,
又点O是AC和BD 的中点,
∴S△ABO=S菱形ABCD, ∴.
(3)①
在菱形,
,
,
,
,
连结交于点,
在中,
∵BF∥AD,
∴△BEF∽△DEA,
∴,
∴,
∴
②
在菱形,
,
,
过点E作的垂线交于点,过点E作的垂线交于点G,E,H,三点共线
由(2)所得,
,
延长过点A作的垂线交于点I,则四边形是矩形,
在中,,
,
,
,
,
,
设
③,不成立(舍去)
综上所述或
(1)根据菱形的性质得出AB=CB,∠ABE=∠CBE,从而利用SAS证得△ABE≌△CBE,从而得出;
(2)连接AC交BD于点O,过点B作BF ∥AC交AE的延长线于点F,首先证明∠BAE=∠EAO,然后再根据BF ∥AC,得出∠EFB=∠EAO,即可得出∠BAE=∠EAO,等角对等边得出AB=BF,再根据△BEF∽△OEA,得出,从而得出,再根据菱形的性质可得S△ABO=S菱形ABCD,即可得出。
(3)因为△CDE是等腰三角形,可分三种情况讨论:①,根据菱形的性质,可得DC=DE=AD=5,即可得出BE=BF=1,根据勾股定理可得AE=,然后根据△BEF∽△DEA,可得出,即可得出EF的长度;②,
在菱形中,,过点E作的垂线交于点,过点E作的垂线交于点G,E,H,三点共线,由(2)所得,;延长过点A作的垂线交于点I,则四边形是矩形,;在中,,;,;设,,③,,不成立(舍去);综上所述或。
23.(1)解:将A(1,3)代入反比例解析式得:,
,
∴反比例解析式为,
将B(-3,n)代入反比例解析式得:,
∴,
∴B(-3,-1),
将A(1,3)与B(-3,-1)代入中,得:
,
解得:,
∴一次函数解析式为;
(2)解:观察图象可得:一次函数值大于反比例函数值的的取值范围为或;
(3)解:∵点C为一次函数与x轴的交点坐标,
令,可得
∴,
即,
∴.
,
,
∵点是轴上的点,
∴设点P(a,0),
∴,
∴,.
∴或.
(1)将点A和点B坐标代入反比例解析式即可求出反比例函数解析式和点B坐标,再将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)一次函数的值大于反比例函数的值,一次函数的图象在反比例函数的图象上方,结合交点坐标,即可得到答案.
(3)先求出点C的坐标,根据面积相等求出PC的长度,进一步求出P点坐标.
(1)解:将A(1,3)代入反比例解析式得:,
,
∴反比例解析式为,
将B(-3,n)代入反比例解析式得:,
∴,
∴B(-3,-1),
将A(1,3)与B(-3,-1)代入中,得:,
解得:,
∴一次函数解析式为;
(2)解:由图象得:一次函数值大于反比例函数值的的取值范围为或;
(3)解:对于一次函数,令,得到,即C(-2,0),
∴.
∵的面积等于的面积,
,
,
∵点是轴上的点,
∴设点P(a,0),
∵C(-2,0),
∴,
解得,.
∴或.
24.(1)解:线段与的数量关系是、位置关系是,
理由如下:
∵四边形是正方形,
∴,,
在和中,
,
,,
,
,则;
(2)解:过点作,如图所示:
正方形的边长为4,
,且,
由(1)知,
在中,,,
点为的中点,
,
∴,
∵在中,,
∴,
∵在中,,,
∴,
∵在中,,
∴,
,
∵在中,,,
∴,
,
∵在中,,,
∴,
,
,
,,
,
的周长为;
(3)解:连接,过作,如图所示:
,,
是线段的垂直平分线,则,
,即是等腰三角形,
,则由勾股定理可得,
过点作,延长,过作于,如图:
∵在中,,
∴,
∵在中,,,
∴,
,
;,
.
同课章节目录
