2024-2025学年八年级下学期数学期考末模拟卷(浙江金华市专用) 【答案+解析】
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末模拟卷(浙江金华市专用) 【答案+解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 668.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:07:00 | ||
图片预览



文档简介
保密★启用前
2024-2025学年八年级下册期末模拟卷(金华市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.若关于 的一元二次方程 有一个实数根为 ,则 的值为( )
A.1 B.3 C.-1 D.-2
3.已知点 , , 都在反比例函数 的图象上,则( )
A. B. C. D.
4.用反证法证明命题“在中,,求证:”,应先假设( )
A. B. C. D.
5.函数,的图象如图所示,下列结论中错误的是( )
A.两函数图象的交点坐标为
B.直线分别与两函数图象交于,两点,则线段的长为3
C.当时,
D.当时,的值随着x值的增大而增大,的值随着x值的增大而减小
6.将一元二次方程化成(a,b为常数)的形式,则a,b的值分别是( )
A. B. C.4,21 D.
7.下列各式中,是最简二次根式的是( )
A. B. C. D.
8.如图,在菱形中,点分别是边的中点,连接.若菱形的面积为16,则的面积为( )
A.8 B.7 C.6 D.5
9.如图,矩形ABCD中,分别是边AD,BC的中点,于P,DP的延长线交AB于.下列结论:①;②;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
10.某个亮度可调节的台灯, 其灯光亮度的改变, 可以通过调节总电阻控制电流的变化来实现。如图所示的是该台灯的电流 (A) 与电阻 的关系图象,该图象经过点 。根据图象可知, 下列说法正确的是 ( )
A.当 时,
B. 与 的函数表达式是
C.当 时,
D.当 时, 则
二、填空题(本题有6小题,每小题3分,共18分)
11.若式子 有意义,则x的取值范围是 .
12.已知a为方程的一个根,则代数式的值为 .
13.甲,乙两位射箭运动员最近5次射击成绩的平均数均为8环,方差分别为:环2,环2,则 (填“甲”或“乙”) 的射击成绩更为稳定.
14.如图,四边形ABCD为平行四边形,延长AD到,使,连结EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
15.如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为 ;②当平分时,正方形的面积为 .
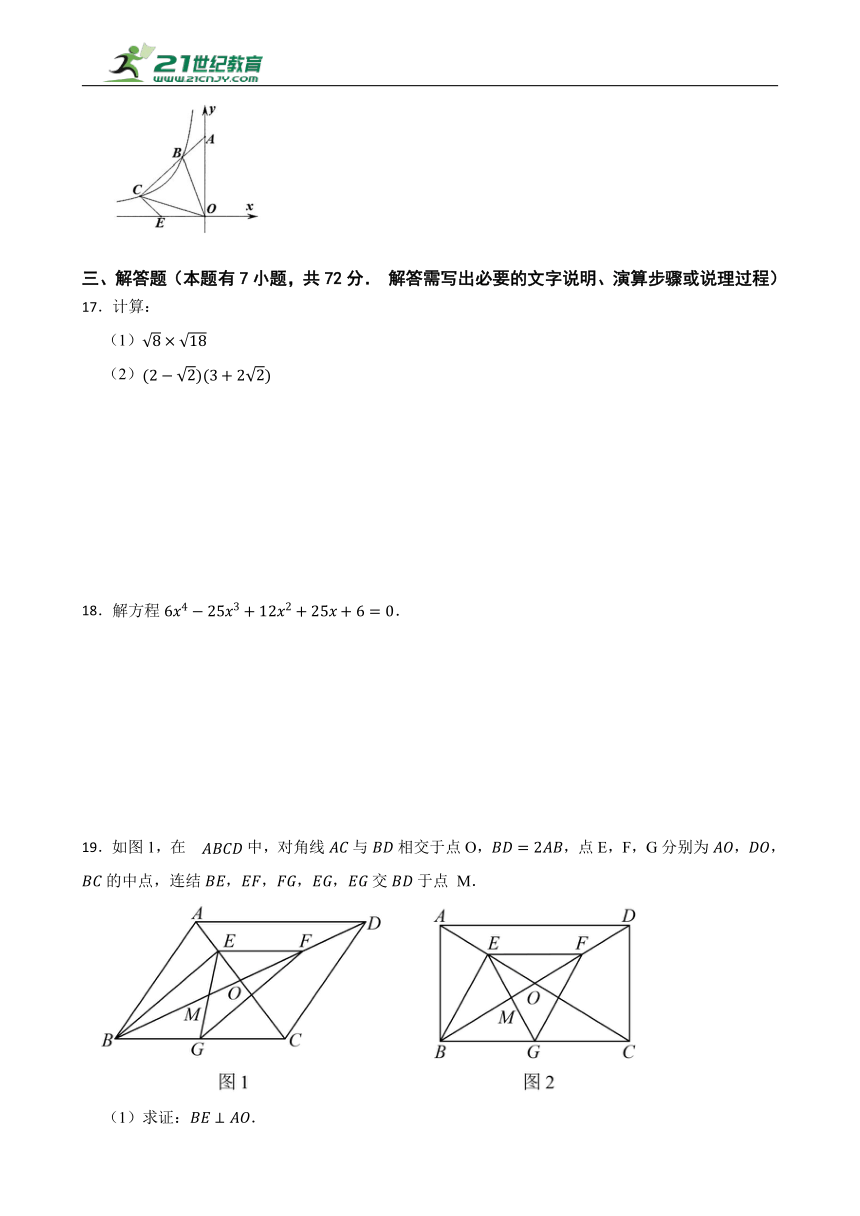
16.如图, 第二象限的点 在反比例函数 图象上, 延长 交 轴于点 , 点 是 轴负半轴上的一点, , 连结 , 若 , 则 的值是 .
三、解答题(本题有7小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.计算:
(1)
(2)
18.解方程.
19.如图1,在中,对角线与相交于点O,,点E,F,G分别为,,的中点,连结,,,,交于点 M.
(1)求证:.
(2)求证:四边形为平行四边形.
(3)如图2,当为矩形时,若,求四边形的面积.
20.学校广播台要招聘一名编辑,甲、乙、丙三位同学报名并参加了3项素质测试,成绩如下表(单位:分).
语言文字能力 运用媒体能力 创意设计能力
甲 86 77 77
乙 76 87 74
丙 80 78 85
(1)计算得甲、乙的平均分分别为80分,79分,请求出丙的平均分,并根据三人的平均分从高到低进行排序;
(2)学校认为:①单项最低分不能低于75分;②三个项目的重要程度有所不同,每位应聘者的语言文字能力、运用媒体能力、创意设计能力的成绩应按的比例计算其成绩,请问谁能成功应聘?
21.如图,菱形中,,点在对角线上,交于点,交于点.
(1)求的度数;
(2)连结,当时,判断与的数量关系并证明.
22.如图,一次函数与反比例函数的图象交于点和点B.
(1)求反比例函数的解析式及点B的坐标.
(2)请直接写出当时,x的取值范围.
(3)点是反比例函数图象上的点,连接AC,BC,求的面积.
23. 杭州亚运会期间,万名志愿者“小青荷”给各方宾友留下了难以忘怀的美好印象.想要成为“小青荷”,必须经过层层考验,下面是亚运会志愿者招募时甲、乙两名报名选手的面试成绩(单位:分):
项目 外语能力 综合素质 形象礼仪 赛事服务经验
甲
乙
(1)如果根据四项成绩的平均分计算最后成绩,甲、乙两人中成绩高的可入选志愿者,请通过计算说明甲、乙两人谁将成为“小青荷”;
(2)如果将外语能力、综合素质、形象礼仪、赛事服务经验按的比例确定最后成绩,甲、乙两人中成绩高的可入选志愿者,请通过计算说明甲、乙两人谁将成为“小青荷”.
24.在菱形ABCD中,是直线BD上一动点,以AP为边向右侧作等边按逆时针排列),点的位置随点的位置变化而变化.
(1)如图1,当点在线段BD上,且点在菱形ABCD内部或边上时,连结CE,小明通过连结AC后证明得到BP与CE的数量关系是 ;
(2)如图2,当点在线段BD上,且点在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)当点P在BD的延长线上时,其他条件不变,连结BE,若,,求PB的长.
答案解析部分
1.C
解:A、 是轴对称图形,故不符合题意;
B、是中心对称图形, 故不符合题意;
C、既是轴对称图形,又是中心对称图形, 故符合题意;
D、是轴对称图形,故不符合题意;
故答案为:C.
中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐项判断即可.
2.A
解:将x=-2代入原方程x2+x-2k=0得,
(-2)2+(-2)-2k=0,
解得k=1.
故答案为:A.
根据方程解的定义,将x=-2代入原方程x2+x-2k=0即可得出关于字母k的方程,求解即可.
3.A
解:函数图象如图所示:
故答案为:A.
画出反比例函数的图象,结合图象进行比较即可.
4.A
解:用反证法证明命题“在中,,求证:”,应先假设,
故答案为:A.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一 一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
5.C
解:将点分别代入两个解析式得,,正确,故A不符合题意;
将分别代入两个函数解析式,,,,正确,故B不符合题意;
当时,,原说法错误,故C符合题意;
当时,的值随着值的增大而增大,的值随着值的增大而减小,正确,故D不符合题意;
故答案为:C.
根据正比例函数和反比例函数性质逐一分析,再作出判断.
6.A
7.C
解:A、,被开方数为,存在分母,不是最简二次根式,不符合题意;
B、,被开方数是25,25=52是完全平方数,即被开方数含能开得尽方的因数,不是最简二次根式,不符合题意;
C、, 被开方数为3,不含分母且无法开方得到整数,是最简二次根式,符合题意;
D、,被开方数27=9×3,27是完全平方数,即被开方数含能开得尽方的因数,不是最简二次根式,不符合题意.
故答案为:C.
被开方数不含分母,且被开方数不含能开得尽方的因数或因式的二次根式,叫做最简二次根式,据此逐一判断得出答案.
8.C
解 :连接和,
∵四边形ABCD是菱形,
∴,,
∴
∵点分别是边的中点,
∴EF是△ADC的中位线,
∴,,
∴,
∵点分别是边的中点,
∴,
∴,
故答案为:C.
先根据菱形的性质求得,再根据三角形的中位线定理,可得,,从而求得,再利用求解.
9.D
解:①∵四边形ABCD是矩形,AD=5,
∴BC=AD=5,
∵CP⊥BE于P,F是BC的中点,
∴PF=BC=×5=2.5,此结论正确;
②∵四边形ABCD是矩形,E、F分别是边AD、BC的中点,
∴DE=BF,AD∥BC,∠DCF=90°,
∴四边形BEDF是平行四边形,
∴BE∥DF,
∵CP⊥BE,
∴CP⊥DF,
由①得:PF=CF=BF=BC=2.5,
∴DF垂直平分PC,
∴PD=CD,
在△DPF和△DCF中,
∴△DPF≌△DCF(SSS)
∴∠DPF=∠DCF=90°,
∴PF⊥DG,此结论正确;
③连接GF,如图,
由①得:PF=BF=CF,
由②得:∠GDF=90°,
在Rt△BFG和Rt△PFG中
∴Rt△BFG≌Rt△PFG(HL)
∴BG=PG,
由②得:△DPF≌△DCF,
∴DP=DC,
∵CD=3,
∴DP=DC=3,
设PG=BG=x,
∴DG=3+x,AG=3-x,
在Rt△ADG中,由勾股定理得:AD2+AG2=DG2,
∴52+(3-x)2=(3+x)2,解得:x=,
即PG=;此结论正确.
∴①②③都正确.
故答案为:D.
①根据直角三角形斜边上的中线等于斜边的一半可求解;
②根据一组对边平行且相等的四边形是平行四边形可得四边形BEDF是平行四边形,则BE∥DF,由平行线的性质可得CP⊥DF,结合①的结论可得DF垂直平分PC,于是用边边边可证△DPF≌△DCF,由全等三角形的性质可求解;
③连接GF,用HL定理可证Rt△BFG≌Rt△PFG,由全等三角形的性质可得BG=PG,设PG=BG=x,在Rt△ADG中,由勾股定理可得关于x的方程,解方程即可求解.
10.D
解:设反比例函数的解析式为,
把点P坐标代入得:,
解得:k=220,
故函数解析式为:,B选项错误,不符合题意;
当I=0.2时,即,
解得:R=1100;A错误,不符合题意;
当R=500时,,
由图象知,当R>500时,I<0.44;C错误,不符合题意;
当R=880时,I=0.25;当R=1000时,,
故当880<R<1000时,则0.22<I<0.25;D正确,符合题意;
故答案为:D.
先根据图象待定系数法求出反比例函数的解析式,再结合图象逐项分析即可求解.
11.
解:x-2≥0,
∴x≥2.
故答案为:x≥2.
根据被开方数为非负数列不等式求解即可.
12.
解:∵a为方程的一个根,
∴
∴
∵
∴
故答案为:-7.
将a代入方程中得到:进而得到:,据此即可求出代数式的值.
13.乙
14.或或等
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AD=DE,
∴BC=DE,
∴四边形BCED是平行四边形,
①若添加CD=BE,
∴平行四边形BCED是矩形;
②若添加∠ADB=90°,
∴∠EDB=90°,
∴平行四边形BCED是矩形;
③若添加CE⊥DE,
∴∠CED=90°,
∴平行四边形BCED是矩形;
∴要使四边形DBCE成为矩形,可添加的一个条件可以是CD=BE或∠ADB=90°或CE⊥DE.
故答案为:CD=BE或∠ADB=90°或CE⊥DE.
由题意,根据一组对边平行且相等的四边形是平行四边形可得四边形BCED是平行四边形,然后根据对角线相等的平行四边形是矩形可添加CD=BE;根据有一个角是直角的平行四边形是矩形可添加∠ADB=90°;根据有一个角是直角的平行四边形是矩形可添加CE⊥DE(答案不唯一).
15.;12
16.-3
如图:作CG⊥x轴,垂足为点G,BH⊥y轴,垂足为点H
∵点B、C在反比例函数图象上,OB=OC∴点B,C关于直线y=-x对称设CG=m∵∠OEC=135°∴∠CEG=45°∴CG=EG=m,CE=∴BC=2CE=2∴OG=OE+EG=2+m∴点C的坐标为(-2-m,m),点B的坐标为(-m,2+m)∴∴2=∴m=1∴点C的坐标为(-3,1)∵点C在反比例函数 图象上∴k=-3.
先通过点B、C在反比例函数图象上,OB=OC,得出:点B,C关于直线y=-x对称,设CG=m得出:CG=EG=m,CE=,则BC=2CE=2,点C的坐标为(-2-m,m),点B的坐标为(-m,2+m),再根据两点之间的坐标公式,计算出BC的长,列出方程解出m,即可求出点C的坐标,代入反比例函数即可求出k的值.
17.(1)12;(2)
18.解:根据题意可知,
∴,
,
,
设,
∴,
∴,
解得:或,即或,
∴或,
解得:,,,,
经检验:,,,是方程的解,
∴,,,.
先根据题意可知,将原方程转化为,设,可得关于a的方程求解求出a,再代回后得到关于x的方程求解,最后求解检验即可.
19.(1)解:,
,互相平分,
,
,
,
点为中点,
;
(2)解:,
,,
点,,分别为,,的中点,
,,,
,,
四边形是平行四边形;
(3)解:如图,过点作于点,
矩形,,
,
∴,
∴,是等边三角形,
,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
四边形的面积.
(1)先根据平行四边形的性质先证明,再根据点为中点可得结论;
(2)先根据三角形中位线定理可得,,再结合平行四边形的性质,证明,,即可得出结论;
(3)先证明是等边三角形,求出,再利用勾股定理求出,得到的长,进而可计算四边形的面积.
20.(1)解:,
三名应聘者的排名顺序为丙,甲,乙;
(2)由题意得:乙不符合条件①,
,
,
,
甲应聘成功.
(1)利用平均数的公式求出丙的成绩,排序即可;
(2)利用加权平均数公式求出甲,丙的成绩,作出决策即可.
21.(1)解:∵,,
∴四边形是平行四边形,
∴.
(2)解:,理由如下:
如图
在菱形中,,,
∵,
∴.(或直接由轴对称性得)
∴,
∵,,
∴,
∵,
∴,
∴,.
∴.
∴.∴.
(1)根据两组对边分别平行的四边形是平行四边形证明四边形是平行四边形,再根据平行四边形的对角相等即可解决问题;
(2)连接PB,根据菱形的性质准备条件,由SAS证明三角形CDP与三角形CBP全等,证得PB=PD,,然后利用菱形的性质和三角形内角和定理证明,得PB=PF,进而可以解决问题.
22.(1)解: 点在图象上,
,
点A的坐标为(1,3)
点A在图象上,
,
反比例函数的解析式 为,
,
解得,,
点B的坐标为.
(2)解:如图,
当时,即的图象在图象的下方时,所对应的自变量的取值范围,
根据图象可得,或.
(3)解: 点是反比例函数图象上的点,
,即,
过点作轴交于点,则点的纵坐标为1,
点在上,纵坐标为1,
横坐标为,
点,
,
,
.
∴的面积为8.
(1)先根据点A在一次函数的图象上,代入可求得点A的坐标,再将点A的坐标代入反比例函数的解析式,可求得反比例函数的解析式,再求出两个函数图象的交点,可求得点B的坐标;
(2)当时,即的图象在图象的下方时,所对应的自变量的取值范围,利用函数图象即可得解;
(3)先求出点C的坐标,再过点作轴交于点,可得点的纵坐标为1,再利用三角形面积公式,可得,代入即可求解.
(1)解: 点在图象上,
,
,
在图象上,
,
,
联立和得,
,
解得,,
点B的坐标为.
(2)解:如图,
当时,即的图象在图象的下方时,所对应的自变量的取值范围,
根据图象可得,或.
(3)解: 点是反比例函数图象上的点,
,即,
过点作轴交于点,则点的纵坐标为1,
点在上,纵坐标为1,
横坐标为,
点,
,
,
.
故的面积为8.
23.(1)解:甲的平均分为,
乙的平均分为,
∵,
∴乙将成为“小青荷”;
(2)解:甲的平均分为,
乙的平均分为,
∵,
∴甲将成为“小青荷”.
()利用算术平均数公式计算出两人的平均分,根据两人的平均分即可判断;
()利用加权平均数公式计算出两人的平均分,根据两人的平均分即可判断;
24.(1)
(2)(1)中的结论仍然成立.
理由如下:如图,连结AC,
菱形,
和都是等边三角形,
,
是等边三角形,
,
,
,
,
.
(1)中的结论仍然成立;
(3)如图,当点在BD的延长线上时,连结AC交BD于点,连结BE,CE,
四边形ABCD是菱形,
平分
同(2)易证,
是正三角形,
(1)BP与CE的数量关系为:BP=CE,
理由如下:∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC,
∴△ABC是等边三角形,
∴∠ABC=∠CAB=60°,
∵△APE是等边三角形,
∴∠PAE=60°,AP=AE,
而∠CAB=∠CAP+∠PAB,∠PAE=∠CAP+∠CAE,
∴∠PAB=∠CAE,
在△ABP和△ACE中
∴△ABP≌△ACE(SAS)
∴BP=CE.
(1)由菱形和等边三角形的性质并用边角边可证△ABP≌△ACE,根据全等三角形的对应边相等即可求解;
(2)(1)中的结论仍然成立.理由如下:如图,连结AC,同理可证△ABP≌△ACE求解;
(3)当点在BD的延长线上时,连结AC交BD于点,连结BE,CE,同理可证△ABP≌△ACE,根据全等三角形的对应角相等可得∠ACE=∠ABO=30°,BP=CE,由(1)可得△ABC是等边三角形,于是由等边三角形的性质和角的构成得∠BCE=∠BCA+∠ACE=90°,在Rt△BCE中,用勾股定理可求得CE的值,然后根据PB=CE可求解.
2024-2025学年八年级下册期末模拟卷(金华市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.若关于 的一元二次方程 有一个实数根为 ,则 的值为( )
A.1 B.3 C.-1 D.-2
3.已知点 , , 都在反比例函数 的图象上,则( )
A. B. C. D.
4.用反证法证明命题“在中,,求证:”,应先假设( )
A. B. C. D.
5.函数,的图象如图所示,下列结论中错误的是( )
A.两函数图象的交点坐标为
B.直线分别与两函数图象交于,两点,则线段的长为3
C.当时,
D.当时,的值随着x值的增大而增大,的值随着x值的增大而减小
6.将一元二次方程化成(a,b为常数)的形式,则a,b的值分别是( )
A. B. C.4,21 D.
7.下列各式中,是最简二次根式的是( )
A. B. C. D.
8.如图,在菱形中,点分别是边的中点,连接.若菱形的面积为16,则的面积为( )
A.8 B.7 C.6 D.5
9.如图,矩形ABCD中,分别是边AD,BC的中点,于P,DP的延长线交AB于.下列结论:①;②;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
10.某个亮度可调节的台灯, 其灯光亮度的改变, 可以通过调节总电阻控制电流的变化来实现。如图所示的是该台灯的电流 (A) 与电阻 的关系图象,该图象经过点 。根据图象可知, 下列说法正确的是 ( )
A.当 时,
B. 与 的函数表达式是
C.当 时,
D.当 时, 则
二、填空题(本题有6小题,每小题3分,共18分)
11.若式子 有意义,则x的取值范围是 .
12.已知a为方程的一个根,则代数式的值为 .
13.甲,乙两位射箭运动员最近5次射击成绩的平均数均为8环,方差分别为:环2,环2,则 (填“甲”或“乙”) 的射击成绩更为稳定.
14.如图,四边形ABCD为平行四边形,延长AD到,使,连结EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
15.如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为 ;②当平分时,正方形的面积为 .
16.如图, 第二象限的点 在反比例函数 图象上, 延长 交 轴于点 , 点 是 轴负半轴上的一点, , 连结 , 若 , 则 的值是 .
三、解答题(本题有7小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.计算:
(1)
(2)
18.解方程.
19.如图1,在中,对角线与相交于点O,,点E,F,G分别为,,的中点,连结,,,,交于点 M.
(1)求证:.
(2)求证:四边形为平行四边形.
(3)如图2,当为矩形时,若,求四边形的面积.
20.学校广播台要招聘一名编辑,甲、乙、丙三位同学报名并参加了3项素质测试,成绩如下表(单位:分).
语言文字能力 运用媒体能力 创意设计能力
甲 86 77 77
乙 76 87 74
丙 80 78 85
(1)计算得甲、乙的平均分分别为80分,79分,请求出丙的平均分,并根据三人的平均分从高到低进行排序;
(2)学校认为:①单项最低分不能低于75分;②三个项目的重要程度有所不同,每位应聘者的语言文字能力、运用媒体能力、创意设计能力的成绩应按的比例计算其成绩,请问谁能成功应聘?
21.如图,菱形中,,点在对角线上,交于点,交于点.
(1)求的度数;
(2)连结,当时,判断与的数量关系并证明.
22.如图,一次函数与反比例函数的图象交于点和点B.
(1)求反比例函数的解析式及点B的坐标.
(2)请直接写出当时,x的取值范围.
(3)点是反比例函数图象上的点,连接AC,BC,求的面积.
23. 杭州亚运会期间,万名志愿者“小青荷”给各方宾友留下了难以忘怀的美好印象.想要成为“小青荷”,必须经过层层考验,下面是亚运会志愿者招募时甲、乙两名报名选手的面试成绩(单位:分):
项目 外语能力 综合素质 形象礼仪 赛事服务经验
甲
乙
(1)如果根据四项成绩的平均分计算最后成绩,甲、乙两人中成绩高的可入选志愿者,请通过计算说明甲、乙两人谁将成为“小青荷”;
(2)如果将外语能力、综合素质、形象礼仪、赛事服务经验按的比例确定最后成绩,甲、乙两人中成绩高的可入选志愿者,请通过计算说明甲、乙两人谁将成为“小青荷”.
24.在菱形ABCD中,是直线BD上一动点,以AP为边向右侧作等边按逆时针排列),点的位置随点的位置变化而变化.
(1)如图1,当点在线段BD上,且点在菱形ABCD内部或边上时,连结CE,小明通过连结AC后证明得到BP与CE的数量关系是 ;
(2)如图2,当点在线段BD上,且点在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;
(3)当点P在BD的延长线上时,其他条件不变,连结BE,若,,求PB的长.
答案解析部分
1.C
解:A、 是轴对称图形,故不符合题意;
B、是中心对称图形, 故不符合题意;
C、既是轴对称图形,又是中心对称图形, 故符合题意;
D、是轴对称图形,故不符合题意;
故答案为:C.
中心对称图形:把一个图形绕着某一点旋转180°后,旋转后的图形能够与原来的图形重合,轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐项判断即可.
2.A
解:将x=-2代入原方程x2+x-2k=0得,
(-2)2+(-2)-2k=0,
解得k=1.
故答案为:A.
根据方程解的定义,将x=-2代入原方程x2+x-2k=0即可得出关于字母k的方程,求解即可.
3.A
解:函数图象如图所示:
故答案为:A.
画出反比例函数的图象,结合图象进行比较即可.
4.A
解:用反证法证明命题“在中,,求证:”,应先假设,
故答案为:A.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一 一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
5.C
解:将点分别代入两个解析式得,,正确,故A不符合题意;
将分别代入两个函数解析式,,,,正确,故B不符合题意;
当时,,原说法错误,故C符合题意;
当时,的值随着值的增大而增大,的值随着值的增大而减小,正确,故D不符合题意;
故答案为:C.
根据正比例函数和反比例函数性质逐一分析,再作出判断.
6.A
7.C
解:A、,被开方数为,存在分母,不是最简二次根式,不符合题意;
B、,被开方数是25,25=52是完全平方数,即被开方数含能开得尽方的因数,不是最简二次根式,不符合题意;
C、, 被开方数为3,不含分母且无法开方得到整数,是最简二次根式,符合题意;
D、,被开方数27=9×3,27是完全平方数,即被开方数含能开得尽方的因数,不是最简二次根式,不符合题意.
故答案为:C.
被开方数不含分母,且被开方数不含能开得尽方的因数或因式的二次根式,叫做最简二次根式,据此逐一判断得出答案.
8.C
解 :连接和,
∵四边形ABCD是菱形,
∴,,
∴
∵点分别是边的中点,
∴EF是△ADC的中位线,
∴,,
∴,
∵点分别是边的中点,
∴,
∴,
故答案为:C.
先根据菱形的性质求得,再根据三角形的中位线定理,可得,,从而求得,再利用求解.
9.D
解:①∵四边形ABCD是矩形,AD=5,
∴BC=AD=5,
∵CP⊥BE于P,F是BC的中点,
∴PF=BC=×5=2.5,此结论正确;
②∵四边形ABCD是矩形,E、F分别是边AD、BC的中点,
∴DE=BF,AD∥BC,∠DCF=90°,
∴四边形BEDF是平行四边形,
∴BE∥DF,
∵CP⊥BE,
∴CP⊥DF,
由①得:PF=CF=BF=BC=2.5,
∴DF垂直平分PC,
∴PD=CD,
在△DPF和△DCF中,
∴△DPF≌△DCF(SSS)
∴∠DPF=∠DCF=90°,
∴PF⊥DG,此结论正确;
③连接GF,如图,
由①得:PF=BF=CF,
由②得:∠GDF=90°,
在Rt△BFG和Rt△PFG中
∴Rt△BFG≌Rt△PFG(HL)
∴BG=PG,
由②得:△DPF≌△DCF,
∴DP=DC,
∵CD=3,
∴DP=DC=3,
设PG=BG=x,
∴DG=3+x,AG=3-x,
在Rt△ADG中,由勾股定理得:AD2+AG2=DG2,
∴52+(3-x)2=(3+x)2,解得:x=,
即PG=;此结论正确.
∴①②③都正确.
故答案为:D.
①根据直角三角形斜边上的中线等于斜边的一半可求解;
②根据一组对边平行且相等的四边形是平行四边形可得四边形BEDF是平行四边形,则BE∥DF,由平行线的性质可得CP⊥DF,结合①的结论可得DF垂直平分PC,于是用边边边可证△DPF≌△DCF,由全等三角形的性质可求解;
③连接GF,用HL定理可证Rt△BFG≌Rt△PFG,由全等三角形的性质可得BG=PG,设PG=BG=x,在Rt△ADG中,由勾股定理可得关于x的方程,解方程即可求解.
10.D
解:设反比例函数的解析式为,
把点P坐标代入得:,
解得:k=220,
故函数解析式为:,B选项错误,不符合题意;
当I=0.2时,即,
解得:R=1100;A错误,不符合题意;
当R=500时,,
由图象知,当R>500时,I<0.44;C错误,不符合题意;
当R=880时,I=0.25;当R=1000时,,
故当880<R<1000时,则0.22<I<0.25;D正确,符合题意;
故答案为:D.
先根据图象待定系数法求出反比例函数的解析式,再结合图象逐项分析即可求解.
11.
解:x-2≥0,
∴x≥2.
故答案为:x≥2.
根据被开方数为非负数列不等式求解即可.
12.
解:∵a为方程的一个根,
∴
∴
∵
∴
故答案为:-7.
将a代入方程中得到:进而得到:,据此即可求出代数式的值.
13.乙
14.或或等
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AD=DE,
∴BC=DE,
∴四边形BCED是平行四边形,
①若添加CD=BE,
∴平行四边形BCED是矩形;
②若添加∠ADB=90°,
∴∠EDB=90°,
∴平行四边形BCED是矩形;
③若添加CE⊥DE,
∴∠CED=90°,
∴平行四边形BCED是矩形;
∴要使四边形DBCE成为矩形,可添加的一个条件可以是CD=BE或∠ADB=90°或CE⊥DE.
故答案为:CD=BE或∠ADB=90°或CE⊥DE.
由题意,根据一组对边平行且相等的四边形是平行四边形可得四边形BCED是平行四边形,然后根据对角线相等的平行四边形是矩形可添加CD=BE;根据有一个角是直角的平行四边形是矩形可添加∠ADB=90°;根据有一个角是直角的平行四边形是矩形可添加CE⊥DE(答案不唯一).
15.;12
16.-3
如图:作CG⊥x轴,垂足为点G,BH⊥y轴,垂足为点H
∵点B、C在反比例函数图象上,OB=OC∴点B,C关于直线y=-x对称设CG=m∵∠OEC=135°∴∠CEG=45°∴CG=EG=m,CE=∴BC=2CE=2∴OG=OE+EG=2+m∴点C的坐标为(-2-m,m),点B的坐标为(-m,2+m)∴∴2=∴m=1∴点C的坐标为(-3,1)∵点C在反比例函数 图象上∴k=-3.
先通过点B、C在反比例函数图象上,OB=OC,得出:点B,C关于直线y=-x对称,设CG=m得出:CG=EG=m,CE=,则BC=2CE=2,点C的坐标为(-2-m,m),点B的坐标为(-m,2+m),再根据两点之间的坐标公式,计算出BC的长,列出方程解出m,即可求出点C的坐标,代入反比例函数即可求出k的值.
17.(1)12;(2)
18.解:根据题意可知,
∴,
,
,
设,
∴,
∴,
解得:或,即或,
∴或,
解得:,,,,
经检验:,,,是方程的解,
∴,,,.
先根据题意可知,将原方程转化为,设,可得关于a的方程求解求出a,再代回后得到关于x的方程求解,最后求解检验即可.
19.(1)解:,
,互相平分,
,
,
,
点为中点,
;
(2)解:,
,,
点,,分别为,,的中点,
,,,
,,
四边形是平行四边形;
(3)解:如图,过点作于点,
矩形,,
,
∴,
∴,是等边三角形,
,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
四边形的面积.
(1)先根据平行四边形的性质先证明,再根据点为中点可得结论;
(2)先根据三角形中位线定理可得,,再结合平行四边形的性质,证明,,即可得出结论;
(3)先证明是等边三角形,求出,再利用勾股定理求出,得到的长,进而可计算四边形的面积.
20.(1)解:,
三名应聘者的排名顺序为丙,甲,乙;
(2)由题意得:乙不符合条件①,
,
,
,
甲应聘成功.
(1)利用平均数的公式求出丙的成绩,排序即可;
(2)利用加权平均数公式求出甲,丙的成绩,作出决策即可.
21.(1)解:∵,,
∴四边形是平行四边形,
∴.
(2)解:,理由如下:
如图
在菱形中,,,
∵,
∴.(或直接由轴对称性得)
∴,
∵,,
∴,
∵,
∴,
∴,.
∴.
∴.∴.
(1)根据两组对边分别平行的四边形是平行四边形证明四边形是平行四边形,再根据平行四边形的对角相等即可解决问题;
(2)连接PB,根据菱形的性质准备条件,由SAS证明三角形CDP与三角形CBP全等,证得PB=PD,,然后利用菱形的性质和三角形内角和定理证明,得PB=PF,进而可以解决问题.
22.(1)解: 点在图象上,
,
点A的坐标为(1,3)
点A在图象上,
,
反比例函数的解析式 为,
,
解得,,
点B的坐标为.
(2)解:如图,
当时,即的图象在图象的下方时,所对应的自变量的取值范围,
根据图象可得,或.
(3)解: 点是反比例函数图象上的点,
,即,
过点作轴交于点,则点的纵坐标为1,
点在上,纵坐标为1,
横坐标为,
点,
,
,
.
∴的面积为8.
(1)先根据点A在一次函数的图象上,代入可求得点A的坐标,再将点A的坐标代入反比例函数的解析式,可求得反比例函数的解析式,再求出两个函数图象的交点,可求得点B的坐标;
(2)当时,即的图象在图象的下方时,所对应的自变量的取值范围,利用函数图象即可得解;
(3)先求出点C的坐标,再过点作轴交于点,可得点的纵坐标为1,再利用三角形面积公式,可得,代入即可求解.
(1)解: 点在图象上,
,
,
在图象上,
,
,
联立和得,
,
解得,,
点B的坐标为.
(2)解:如图,
当时,即的图象在图象的下方时,所对应的自变量的取值范围,
根据图象可得,或.
(3)解: 点是反比例函数图象上的点,
,即,
过点作轴交于点,则点的纵坐标为1,
点在上,纵坐标为1,
横坐标为,
点,
,
,
.
故的面积为8.
23.(1)解:甲的平均分为,
乙的平均分为,
∵,
∴乙将成为“小青荷”;
(2)解:甲的平均分为,
乙的平均分为,
∵,
∴甲将成为“小青荷”.
()利用算术平均数公式计算出两人的平均分,根据两人的平均分即可判断;
()利用加权平均数公式计算出两人的平均分,根据两人的平均分即可判断;
24.(1)
(2)(1)中的结论仍然成立.
理由如下:如图,连结AC,
菱形,
和都是等边三角形,
,
是等边三角形,
,
,
,
,
.
(1)中的结论仍然成立;
(3)如图,当点在BD的延长线上时,连结AC交BD于点,连结BE,CE,
四边形ABCD是菱形,
平分
同(2)易证,
是正三角形,
(1)BP与CE的数量关系为:BP=CE,
理由如下:∵四边形ABCD是菱形,∠ABC=60°,
∴AB=BC,
∴△ABC是等边三角形,
∴∠ABC=∠CAB=60°,
∵△APE是等边三角形,
∴∠PAE=60°,AP=AE,
而∠CAB=∠CAP+∠PAB,∠PAE=∠CAP+∠CAE,
∴∠PAB=∠CAE,
在△ABP和△ACE中
∴△ABP≌△ACE(SAS)
∴BP=CE.
(1)由菱形和等边三角形的性质并用边角边可证△ABP≌△ACE,根据全等三角形的对应边相等即可求解;
(2)(1)中的结论仍然成立.理由如下:如图,连结AC,同理可证△ABP≌△ACE求解;
(3)当点在BD的延长线上时,连结AC交BD于点,连结BE,CE,同理可证△ABP≌△ACE,根据全等三角形的对应角相等可得∠ACE=∠ABO=30°,BP=CE,由(1)可得△ABC是等边三角形,于是由等边三角形的性质和角的构成得∠BCE=∠BCA+∠ACE=90°,在Rt△BCE中,用勾股定理可求得CE的值,然后根据PB=CE可求解.
同课章节目录
