2024-2025学年八年级下学期数学期考末模拟卷(浙江临海市专用) 【答案+解析】
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末模拟卷(浙江临海市专用) 【答案+解析】 | 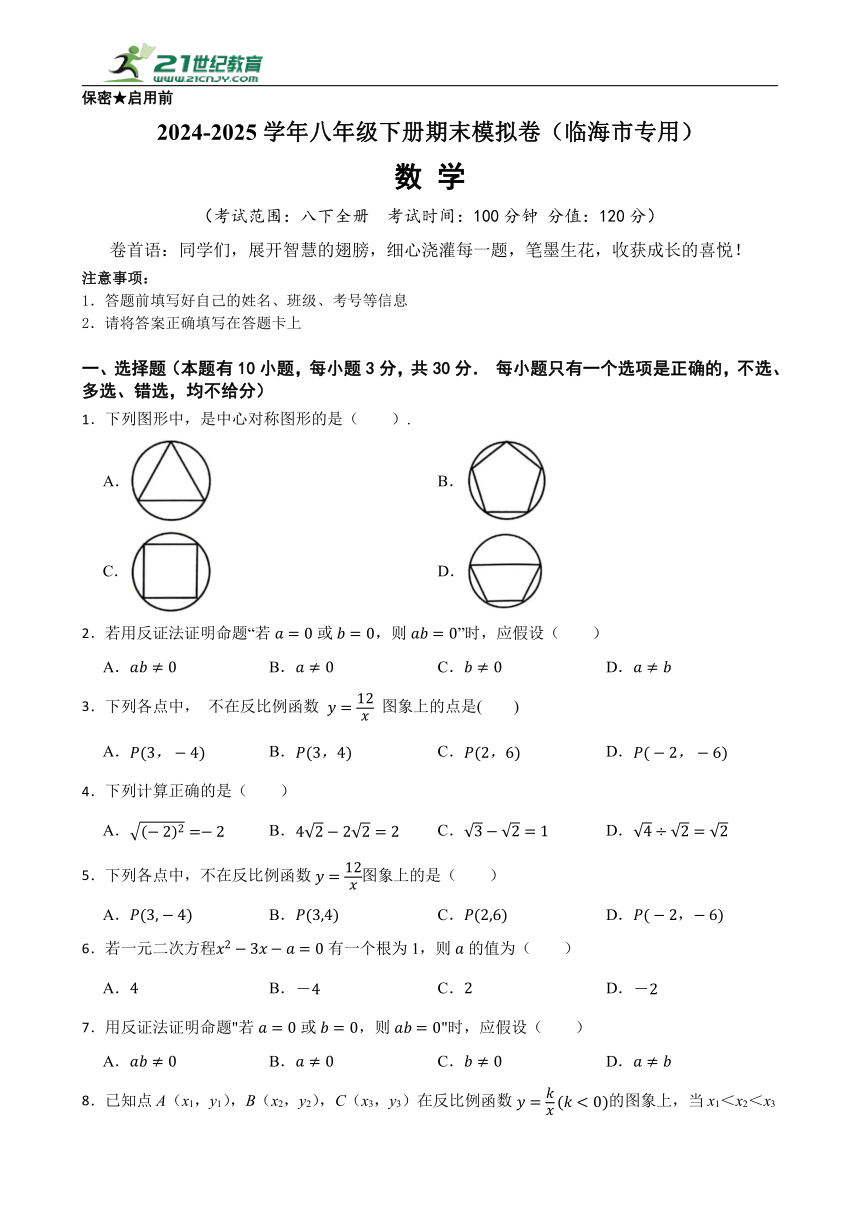 | |
| 格式 | docx | ||
| 文件大小 | 435.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:10:52 | ||
图片预览




文档简介
保密★启用前
2024-2025学年八年级下册期末模拟卷(临海市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,是中心对称图形的是( ).
A. B.
C. D.
2.若用反证法证明命题“若或,则”时,应假设( )
A. B. C. D.
3.下列各点中, 不在反比例函数 图象上的点是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.下列各点中,不在反比例函数图象上的是( )
A. B. C. D.,
6.若一元二次方程有一个根为1,则的值为( )
A. B. C. D.
7.用反证法证明命题"若或,则"时,应假设( )
A. B. C. D.
8.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上,当x1<x2<x3时,则下列判断正确的是( )
A.若x1+x2<0,则y2 y3>0 B.若y1 y3<0,则x2 x3>0
C.若x2+x3<0,则y1 y2>0 D.若y2 y3<0,则x1 x3>0
9.如图, 直线 与 轴, 轴分别交于点 , 点 为第一象限内一点, 以 , 为邻边向右作 , 若 的面积为 12 , 则直线 必经过一点, 这个点的坐标为( )
A. B. C. D.
10.如图,矩形ABCD中,分别是边AD,BC的中点,于P,DP的延长线交AB于.下列结论:①;②;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(本题有6小题,每小题3分,共18分)
11.请写出一个的值: ,使二次根式在实数范围内有意义.
12.已知关于x的一元二次方程的一个根是3,则 .
13.已知一组数据,,,的平均数是5,则另一组数据,,,的平均数是 .
14.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
15.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为 .
如图, 若点 在反比例函数 的一支图象上, 轴于点 ,则 的面积为 。
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1);
(2).
18.先化简,再求值:,其中.
小亮: 解:原式 小芳: 解:原式
(1)____的解答过程是错误的;
(2)先化简,再求值:,其中.
19.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
20.为了解某电影在五一假期的上映满意度,随机抽取了部分观众,对这部电影进行打分(打分按从高到低分为5个分值:5分,4分,3分,2分,1分),根据调查结果,绘制出如图所示的统计图.
(1)分别求这组打分数据的平均数、众数和中位数;
(2)后来又另外随机抽取几名观众对这部电影进行打分,得知这几名观众的打分均小于4分,将这次打分的数据与之前的数据合并后发现中位数发生了改变,则后来最少随机抽取了__________名观众.
21.如图,在等腰三角形纸片ABC中,AB=AC,AD⊥BC于点D,BC=2,,沿AD剪成两个三角形,用这两个三角形拼成平行四边形,请你画出所有符合条件的平行四边形(可在备用图中画),并求出对应平行四边形较长对角线的长.
22.如表是小明这一学期数学成绩测试记录,根据表格提供的信息,回答下列问题:
测试 平时成绩 期中测试 期末测试
练习一 练习二 练习三 练习四
成绩 88 92 90 86 90 96
(1)求小明6次成绩的众数与中位数;
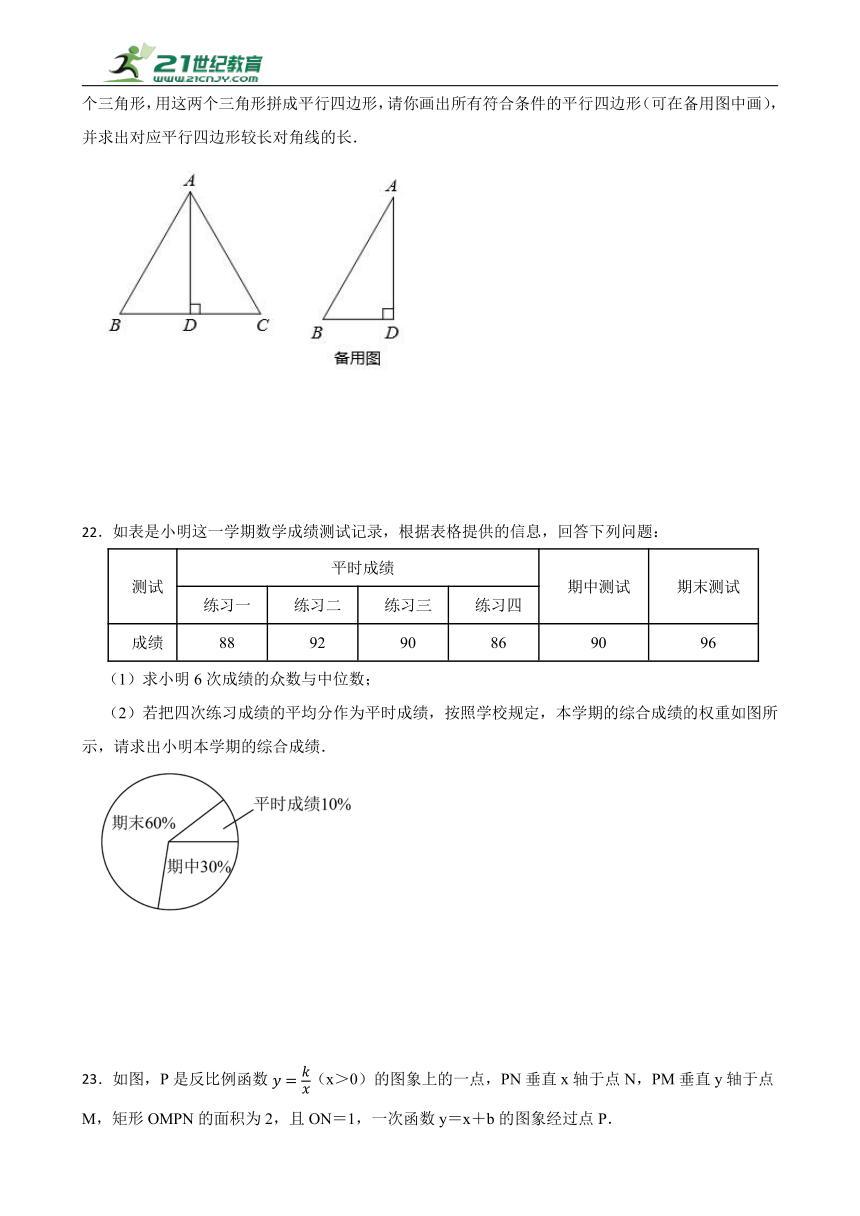
(2)若把四次练习成绩的平均分作为平时成绩,按照学校规定,本学期的综合成绩的权重如图所示,请求出小明本学期的综合成绩.
23.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
24.如图1,在中,对角线AC与BD交于点,点关于AC的对称点为点,连结.
(1)求证:.
(2)当,且时.
①如图2,若三点共线,求四边形的周长.
②如图3,若,求四边形的面积(直接写出答案).
答案解析部分
1.C
解:A,B,D不是中心对称图形;C是中心对称图形;
故答案为:C.
在平面内,把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形就是中心对称图形,据此进行判断即可。
2.A
解:由反证法知第一步应假设该命题的结论“”的反面成立,即,
故选A.
反证法的步骤中,第一步是假设结论不成立.
3.A
解:x=3代入反比例函数 ,得y=4,即(3,4)在反比例函数,故A符合题意,B不符合题意;x=2代入反比例函数 ,得y=6,即(2,6)在反比例函数,故C不符合题意;x=-2代入反比例函数 ,得y=-6,即(-2,-6)在反比例函数,故D符合题意.
故答案为:A.
根据反比例函数的定义,分别将x=2,3,-2代入函数,求出对应的函数值,即可判断.
4.D
A.≠-2,原等式不成立,此选项不符合题意;
B.≠2,原等式不成立,此选项不符合题意;
C.和不是同类二次根式,不能合并,原等式不成立,此选项不符合题意;
D.,原等式成立,此选项符合题意.
故答案为:D.
根据二次根式的减法和二次根式的除法运算法则计算各选项,依次判断即可求解.
5.A
解:A、∵3×(-4)=-12≠12,∴点P(3,-4)不在反比例函数的图象上,此选项符合题意;
B、∵3×4=12,∴点P(3,-4)在反比例函数的图象上,此选项不符合题意;
C、∵2×6=12,∴点P(2,6)在反比例函数的图象上,此选项不符合题意;
D、∵-2×(-6)=12,∴点P(3,-4)在反比例函数的图象上,此选项不符合题意.
故答案为:A.
由题意,求出每一个选项中点P的横、纵坐标的乘积,观察乘积是否等于12即可判断求解.
6.D
7.A
解: "若或,则"时,
第一步应假设:ab≠0.
故答案为:A.
用反证法证明的步骤中,第一步是假设结论不成立,反面成立,由此可判断求解.
8.C
解: 反比例函数的图象 位于二、四象限,
当x1<x2<x3时 ,
A、 若x1+x2<0, 则,且x1<0<x2或x1<x2<0,
∴y2 y3<0 或y2 y3>0 ,故不符合题意;
B、若y1 y3<0,则x1<0<x2或x1<x2<0<x3或x1<x2<0<x3,
∴x2 x3<0 ,故不符合题意;
C、若x2+x3<0,则且x1<x2<0<x3或x1<x2<x3<0,
∴y1 y2>0 ,故符合题意;
D、若y2 y3<0, 则x1<x2<0<x3,
∴x1 x3<0 ,故不符合题意;
故答案为:C.
由反比例函数的图象 位于二、四象限,根据x1<x2<x3时及反比例函数图象上点的坐标特征逐项判断即可.
9.D
解:如图:过B作BM⊥y轴交CD于M,连接AM作AH⊥BM于H
把x=0代入中得:
y=6
∴点B的坐标为(0,6)
∴AH=OB=6
∵四边形ABCD为平行四边形
∵△ABM与平行四边形ABCD同底等高
∴
∴
∴,解得:BM=2
∴M(2,6)
∴直线CD必经过点M(2,6).
故答案为D
先令x=0,求出y的值,得出点B的坐标,即求出OB和AH的长,再根据△ABM与平行四边形ABCD同底等高,得到:,再根据三角形的面积公式求出BM的长,即可知道点M的坐标.
10.D
解:连接GF,
∵矩形,
∴,,,,
∵,是边的中点,
∴,故①正确;
∵分别是边,的中点,
∴
∴四边形是平行四边形
∴
∴
∵
∴垂直平分
∴
∴()
∴,即,故②正确;
∵,,,
∴()
∴,
设,则,,
在中,,
∴解得,即,故③正确;
综上所述,正确的是①②③
故选:D.
① 由于矩形的对边相等,因此BC=AD=5,因为PF是直角三角形PBC斜边BC上的中线,所以PF=2.5,正确;
② 连接,由矩形的性质结合中点的概念可证四边形DEBF是平行四边形,则BE平行DF,由平行线的性质结合直角三角形斜边上的中线等于斜边的一半可证,又FD是公共边,则、即,正确;
③ 由HL可证, 则PG=BG,设BG=x,则AG=3-x,DG=3+x,在中应用勾股定理即可.
11.2024
12.3
解:把3代入方程得:,
解得:,
故答案为:.
把代入方程,可得到关于a的方程,解方程求出a的值.
13.20
解:∵数据,,,的平均数是5,
∴,
∴数据,,,的平均数为:
.
故答案为:20.
根据算术平均数的定义,先求得,然后再利用平均数公式计算,,,的平均数,将整体代入进去即可求解.
14.
解:如图,在上截取,连接并延长,作,
四边形是平行四边形,,,
,,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
,
,
,
当点是边延长线上时,点在的延长线上 ,
,,
,
的最小值是,
故答案为:.
利用瓜豆原理可知点F的运动轨迹是一条直线,故勾手拉手全等三角形模型是本题的解题关键.利用等边三角形的性质通过SAS判定得到,再通过直角三角形的性质求得CM的长度即FC的最小值.
15.
解:将△AMD绕点A逆时针旋转60°得到△AGF,
由旋转的性质可知:MD=FG,AM=AG,△ADF和△AMG均为等边三角形,
∴AM=MG,
∴MA+MD+ME=GM+FG+ME,
∴FM、MG、ME共线时最短,
过点F作FH⊥BC于点H,则FN⊥AD,如图所示:
∵△ADF为等边三角形,
∴ND=AD=3,
∴FN==,
∵四边形ABCD是矩形,
∴NH=AB=4,
∵点E为动点,
∴当FE⊥BC时最短,此时FE=FH=FN+NF=
∴MA+MD+ME的最小值为,
故答案为:
将△AMD绕点A逆时针旋转60°得到△AGF,则MD=FG,AM=AG,△ADF和△AMG均为等边三角形,推出AM=MG求得MA+MD+ME=GM+FG+ME,当FM、MG、ME共线时最短,由于点E也为动点,可得当FE⊥BC时最短,此时易求得FE=FH=FN+NF=.
16.1.5
解:∵|k|=|-3|=3,AM⊥x
∴.
故答案为:1.5.
】根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即,即可求解.
17.(1)
(2)
18.(1)小亮
(2),
19.(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
在△AOE和△COF中
∴△AOE≌△COF(AAS),
∴OE=OF
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
答:AD的长为9
(1)先由平行四边形的性质得到AO=CO,AD∥BC,则∠OAE=∠OCF,∠OEA=∠OFC,结合已知,用角角边即可证△AOE≌△COF,由全等三角形的性质“全等三角形的对应边相等”即可求解;
(2)由(1)中的全等三角形可得OE=OF=3.5,得到EF=7,再由AD∥BC,EF⊥AD,得到EF的长即为平行四边形ABCD中AD边上的高,然后根据平行四边形面积公式计算即可求解.
(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
20.(1)平均分为,众数为5,中位数为4
(2)
21.解:,
①当以AB为对角线剪拼时,如图1所示:
此时两条对角线相等,其长为;
②当以AD为对角线剪拼时,如图2所示:
过点作BD延长线的垂线,垂足为点,
四边形ADEC是矩形,
该平行四边形中较长对角线的长为;
③当以BD为对角线剪拼时,如图3所示:
过点作AD延长线的垂线,垂足为点,
同理可证四边形为矩形,
该平行四边形中较长对角线的长为.
综上所述:所拼平行四边形中较长对角线的长为2或或.
本题主要考查等腰三角形的性质,平行四边形的性质,矩形的性质以及勾股定理的运用,分类讨论思想的运用,属于较难题型.
首先利用等腰三角形的性质及勾股定理求得AB的长,然后分别以AB,AD,BD为对角线平成平行四边形,画出示意图,然后利用矩形的性质及勾股定理进行求解即可.
22.(1)众数为,中位数为
(2)
23.(1),
(2)(0,1)和(0,-1)
24.(1)解:,且点与关于AC对称,
.
.
(2)①三点共线,且点与关于AC对称,
.
,
.
为等腰直角三角形.
.
,
.
四边形是平行四边形.
.
.
②过点作的平行线,交分别于点E,F.则四边形为平行四边形,
所以根据可得.
同时,易证为AD中点,为AE中点,则.
设,则.
在Rt中,,
解,得.
.
.
解:(2)②过点C作OB'的平行线,交AD、B'D分别于点E,F,
∵点B与点B'关于AC对称,
∴∠AOB=∠AOB'=∠COD,
∵∠AOB'+∠B'OD+∠COD=2∠AOB'+∠B'OD=180°,∠OB'D+∠B'DO+∠B'OD=2∠OB'D+∠B'OD=180°,
∴∠OB'D=∠AOB',
∴AC∥B'D,
又∵OB'∥CF,
∴四边形OCFB'是平行四边形,
∴CF=OB',
∵AC∥B'D,
∴∠CAD=∠ADF=∠CAD,
在△EFD与△ECD中,∠FED=∠CED,ED=ED,∠EDF=∠EDC,
∴△EDF≌△EDC,
∴EF=EC,
∵四边形ABCD是平行四边形,
∴AB=CD=AC,AD=BC=8,OA=OC,
又∵CE⊥AD,
∴AE=DE=AD=4,
∵OB'∥CF,且OA=OC,
∴AH=HE=AE=2,CE=2OH,
设,则.
在Rt中,,
解,得.
.
.
(1)由平行四边形的对角线互相平分得DO=BO,由轴对称性质得OB=OB',则OB'=OD,然后根据等边对等角可得结论;
(2)①由轴对称性质得AB=AB',∠BAC=∠B'AC=90°,则△ABC是等腰直角三角形,由等腰直角三角形的性质及勾股定理可得;由平行四边形的对边平行且相等可推出AB'∥CD,且AB'=CD,由一组对边平行且相等的四边形是平行四边形得出四边形ACDB'是平行四边形,进而根据平行四边形轴上计算方法可算出答案;
②过C作OB'的平行线,交AD、B'D分别于点E,F,由轴对称的性质及对顶角相等得∠AOB=∠AOB'=∠COD,由三角形的内角和定理及平角定义推出∠OB'D=∠AOB',由内错角相等两直线平行得AC∥B'D,由两组对边分别平行的四边形是平行四边形得四边形OCFB'是平行四边形,由平行四边形的对边相等得CF=OB',由二直线平行,内错角相等及等量代换得∠CAD=∠ADF=∠CAD,用ASA判断出△EDF≌△EDC,由全等三角形的对应边相等得EF=EC;由平行四边形性质得AB=CD=AC,AD=BC=8,OA=OC,有等腰三角形的三线合一得AE=DE=AD=4,由三角形的中位线定理得AH=HE=AE=2,CE=2OH,设OH=x,则CE=EF=2x,OD=OB'=CF=4x,在Rt△OHD中,利用勾股定理建立方程求出x的值,从而得出CE、HB'的长,最后根据三角形面积公式,由列式计算即可.
2024-2025学年八年级下册期末模拟卷(临海市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,是中心对称图形的是( ).
A. B.
C. D.
2.若用反证法证明命题“若或,则”时,应假设( )
A. B. C. D.
3.下列各点中, 不在反比例函数 图象上的点是( )
A. B. C. D.
4.下列计算正确的是( )
A. B. C. D.
5.下列各点中,不在反比例函数图象上的是( )
A. B. C. D.,
6.若一元二次方程有一个根为1,则的值为( )
A. B. C. D.
7.用反证法证明命题"若或,则"时,应假设( )
A. B. C. D.
8.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数的图象上,当x1<x2<x3时,则下列判断正确的是( )
A.若x1+x2<0,则y2 y3>0 B.若y1 y3<0,则x2 x3>0
C.若x2+x3<0,则y1 y2>0 D.若y2 y3<0,则x1 x3>0
9.如图, 直线 与 轴, 轴分别交于点 , 点 为第一象限内一点, 以 , 为邻边向右作 , 若 的面积为 12 , 则直线 必经过一点, 这个点的坐标为( )
A. B. C. D.
10.如图,矩形ABCD中,分别是边AD,BC的中点,于P,DP的延长线交AB于.下列结论:①;②;③.其中结论正确的有( )
A.①② B.②③ C.①③ D.①②③
二、填空题(本题有6小题,每小题3分,共18分)
11.请写出一个的值: ,使二次根式在实数范围内有意义.
12.已知关于x的一元二次方程的一个根是3,则 .
13.已知一组数据,,,的平均数是5,则另一组数据,,,的平均数是 .
14.如图,在平行四边形中,,,是边延长线上一点,连接,以为边作等边三角形,连接,则的最小值是 .
15.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为 .
如图, 若点 在反比例函数 的一支图象上, 轴于点 ,则 的面积为 。
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1);
(2).
18.先化简,再求值:,其中.
小亮: 解:原式 小芳: 解:原式
(1)____的解答过程是错误的;
(2)先化简,再求值:,其中.
19.如图,在□ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S ABCD=63,OE=3.5,求AD的长.
20.为了解某电影在五一假期的上映满意度,随机抽取了部分观众,对这部电影进行打分(打分按从高到低分为5个分值:5分,4分,3分,2分,1分),根据调查结果,绘制出如图所示的统计图.
(1)分别求这组打分数据的平均数、众数和中位数;
(2)后来又另外随机抽取几名观众对这部电影进行打分,得知这几名观众的打分均小于4分,将这次打分的数据与之前的数据合并后发现中位数发生了改变,则后来最少随机抽取了__________名观众.
21.如图,在等腰三角形纸片ABC中,AB=AC,AD⊥BC于点D,BC=2,,沿AD剪成两个三角形,用这两个三角形拼成平行四边形,请你画出所有符合条件的平行四边形(可在备用图中画),并求出对应平行四边形较长对角线的长.
22.如表是小明这一学期数学成绩测试记录,根据表格提供的信息,回答下列问题:
测试 平时成绩 期中测试 期末测试
练习一 练习二 练习三 练习四
成绩 88 92 90 86 90 96
(1)求小明6次成绩的众数与中位数;
(2)若把四次练习成绩的平均分作为平时成绩,按照学校规定,本学期的综合成绩的权重如图所示,请求出小明本学期的综合成绩.
23.如图,P是反比例函数(x>0)的图象上的一点,PN垂直x轴于点N,PM垂直y轴于点M,矩形OMPN的面积为2,且ON=1,一次函数y=x+b的图象经过点P.
(1)求该反比例函数和一次函数的解析式;
(2)设直线y=x+b与x轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的时,直接写出点Q的坐标.
24.如图1,在中,对角线AC与BD交于点,点关于AC的对称点为点,连结.
(1)求证:.
(2)当,且时.
①如图2,若三点共线,求四边形的周长.
②如图3,若,求四边形的面积(直接写出答案).
答案解析部分
1.C
解:A,B,D不是中心对称图形;C是中心对称图形;
故答案为:C.
在平面内,把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形就是中心对称图形,据此进行判断即可。
2.A
解:由反证法知第一步应假设该命题的结论“”的反面成立,即,
故选A.
反证法的步骤中,第一步是假设结论不成立.
3.A
解:x=3代入反比例函数 ,得y=4,即(3,4)在反比例函数,故A符合题意,B不符合题意;x=2代入反比例函数 ,得y=6,即(2,6)在反比例函数,故C不符合题意;x=-2代入反比例函数 ,得y=-6,即(-2,-6)在反比例函数,故D符合题意.
故答案为:A.
根据反比例函数的定义,分别将x=2,3,-2代入函数,求出对应的函数值,即可判断.
4.D
A.≠-2,原等式不成立,此选项不符合题意;
B.≠2,原等式不成立,此选项不符合题意;
C.和不是同类二次根式,不能合并,原等式不成立,此选项不符合题意;
D.,原等式成立,此选项符合题意.
故答案为:D.
根据二次根式的减法和二次根式的除法运算法则计算各选项,依次判断即可求解.
5.A
解:A、∵3×(-4)=-12≠12,∴点P(3,-4)不在反比例函数的图象上,此选项符合题意;
B、∵3×4=12,∴点P(3,-4)在反比例函数的图象上,此选项不符合题意;
C、∵2×6=12,∴点P(2,6)在反比例函数的图象上,此选项不符合题意;
D、∵-2×(-6)=12,∴点P(3,-4)在反比例函数的图象上,此选项不符合题意.
故答案为:A.
由题意,求出每一个选项中点P的横、纵坐标的乘积,观察乘积是否等于12即可判断求解.
6.D
7.A
解: "若或,则"时,
第一步应假设:ab≠0.
故答案为:A.
用反证法证明的步骤中,第一步是假设结论不成立,反面成立,由此可判断求解.
8.C
解: 反比例函数的图象 位于二、四象限,
当x1<x2<x3时 ,
A、 若x1+x2<0, 则,且x1<0<x2或x1<x2<0,
∴y2 y3<0 或y2 y3>0 ,故不符合题意;
B、若y1 y3<0,则x1<0<x2或x1<x2<0<x3或x1<x2<0<x3,
∴x2 x3<0 ,故不符合题意;
C、若x2+x3<0,则且x1<x2<0<x3或x1<x2<x3<0,
∴y1 y2>0 ,故符合题意;
D、若y2 y3<0, 则x1<x2<0<x3,
∴x1 x3<0 ,故不符合题意;
故答案为:C.
由反比例函数的图象 位于二、四象限,根据x1<x2<x3时及反比例函数图象上点的坐标特征逐项判断即可.
9.D
解:如图:过B作BM⊥y轴交CD于M,连接AM作AH⊥BM于H
把x=0代入中得:
y=6
∴点B的坐标为(0,6)
∴AH=OB=6
∵四边形ABCD为平行四边形
∵△ABM与平行四边形ABCD同底等高
∴
∴
∴,解得:BM=2
∴M(2,6)
∴直线CD必经过点M(2,6).
故答案为D
先令x=0,求出y的值,得出点B的坐标,即求出OB和AH的长,再根据△ABM与平行四边形ABCD同底等高,得到:,再根据三角形的面积公式求出BM的长,即可知道点M的坐标.
10.D
解:连接GF,
∵矩形,
∴,,,,
∵,是边的中点,
∴,故①正确;
∵分别是边,的中点,
∴
∴四边形是平行四边形
∴
∴
∵
∴垂直平分
∴
∴()
∴,即,故②正确;
∵,,,
∴()
∴,
设,则,,
在中,,
∴解得,即,故③正确;
综上所述,正确的是①②③
故选:D.
① 由于矩形的对边相等,因此BC=AD=5,因为PF是直角三角形PBC斜边BC上的中线,所以PF=2.5,正确;
② 连接,由矩形的性质结合中点的概念可证四边形DEBF是平行四边形,则BE平行DF,由平行线的性质结合直角三角形斜边上的中线等于斜边的一半可证,又FD是公共边,则、即,正确;
③ 由HL可证, 则PG=BG,设BG=x,则AG=3-x,DG=3+x,在中应用勾股定理即可.
11.2024
12.3
解:把3代入方程得:,
解得:,
故答案为:.
把代入方程,可得到关于a的方程,解方程求出a的值.
13.20
解:∵数据,,,的平均数是5,
∴,
∴数据,,,的平均数为:
.
故答案为:20.
根据算术平均数的定义,先求得,然后再利用平均数公式计算,,,的平均数,将整体代入进去即可求解.
14.
解:如图,在上截取,连接并延长,作,
四边形是平行四边形,,,
,,
,
,
是等边三角形,
,,
是等边三角形,
,,
,
,
,
,
当点是边延长线上时,点在的延长线上 ,
,,
,
的最小值是,
故答案为:.
利用瓜豆原理可知点F的运动轨迹是一条直线,故勾手拉手全等三角形模型是本题的解题关键.利用等边三角形的性质通过SAS判定得到,再通过直角三角形的性质求得CM的长度即FC的最小值.
15.
解:将△AMD绕点A逆时针旋转60°得到△AGF,
由旋转的性质可知:MD=FG,AM=AG,△ADF和△AMG均为等边三角形,
∴AM=MG,
∴MA+MD+ME=GM+FG+ME,
∴FM、MG、ME共线时最短,
过点F作FH⊥BC于点H,则FN⊥AD,如图所示:
∵△ADF为等边三角形,
∴ND=AD=3,
∴FN==,
∵四边形ABCD是矩形,
∴NH=AB=4,
∵点E为动点,
∴当FE⊥BC时最短,此时FE=FH=FN+NF=
∴MA+MD+ME的最小值为,
故答案为:
将△AMD绕点A逆时针旋转60°得到△AGF,则MD=FG,AM=AG,△ADF和△AMG均为等边三角形,推出AM=MG求得MA+MD+ME=GM+FG+ME,当FM、MG、ME共线时最短,由于点E也为动点,可得当FE⊥BC时最短,此时易求得FE=FH=FN+NF=.
16.1.5
解:∵|k|=|-3|=3,AM⊥x
∴.
故答案为:1.5.
】根据过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,即,即可求解.
17.(1)
(2)
18.(1)小亮
(2),
19.(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
在△AOE和△COF中
∴△AOE≌△COF(AAS),
∴OE=OF
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
答:AD的长为9
(1)先由平行四边形的性质得到AO=CO,AD∥BC,则∠OAE=∠OCF,∠OEA=∠OFC,结合已知,用角角边即可证△AOE≌△COF,由全等三角形的性质“全等三角形的对应边相等”即可求解;
(2)由(1)中的全等三角形可得OE=OF=3.5,得到EF=7,再由AD∥BC,EF⊥AD,得到EF的长即为平行四边形ABCD中AD边上的高,然后根据平行四边形面积公式计算即可求解.
(1)解:∵四边形ABCD是平行四边形,O是AC与BD的交点,
∴AO=CO,AD∥BC,
∴∠OAE=∠OCF,∠OEA=∠OFC,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:由(1)得OE=OF=3.5,
∴EF=7,
∵AD∥BC,EF⊥AD,
∴EF的长即为平行四边形ABCD中AD边上的高,
∵四边形ABCD的面积为63,
∴,
∴AD=9.
20.(1)平均分为,众数为5,中位数为4
(2)
21.解:,
①当以AB为对角线剪拼时,如图1所示:
此时两条对角线相等,其长为;
②当以AD为对角线剪拼时,如图2所示:
过点作BD延长线的垂线,垂足为点,
四边形ADEC是矩形,
该平行四边形中较长对角线的长为;
③当以BD为对角线剪拼时,如图3所示:
过点作AD延长线的垂线,垂足为点,
同理可证四边形为矩形,
该平行四边形中较长对角线的长为.
综上所述:所拼平行四边形中较长对角线的长为2或或.
本题主要考查等腰三角形的性质,平行四边形的性质,矩形的性质以及勾股定理的运用,分类讨论思想的运用,属于较难题型.
首先利用等腰三角形的性质及勾股定理求得AB的长,然后分别以AB,AD,BD为对角线平成平行四边形,画出示意图,然后利用矩形的性质及勾股定理进行求解即可.
22.(1)众数为,中位数为
(2)
23.(1),
(2)(0,1)和(0,-1)
24.(1)解:,且点与关于AC对称,
.
.
(2)①三点共线,且点与关于AC对称,
.
,
.
为等腰直角三角形.
.
,
.
四边形是平行四边形.
.
.
②过点作的平行线,交分别于点E,F.则四边形为平行四边形,
所以根据可得.
同时,易证为AD中点,为AE中点,则.
设,则.
在Rt中,,
解,得.
.
.
解:(2)②过点C作OB'的平行线,交AD、B'D分别于点E,F,
∵点B与点B'关于AC对称,
∴∠AOB=∠AOB'=∠COD,
∵∠AOB'+∠B'OD+∠COD=2∠AOB'+∠B'OD=180°,∠OB'D+∠B'DO+∠B'OD=2∠OB'D+∠B'OD=180°,
∴∠OB'D=∠AOB',
∴AC∥B'D,
又∵OB'∥CF,
∴四边形OCFB'是平行四边形,
∴CF=OB',
∵AC∥B'D,
∴∠CAD=∠ADF=∠CAD,
在△EFD与△ECD中,∠FED=∠CED,ED=ED,∠EDF=∠EDC,
∴△EDF≌△EDC,
∴EF=EC,
∵四边形ABCD是平行四边形,
∴AB=CD=AC,AD=BC=8,OA=OC,
又∵CE⊥AD,
∴AE=DE=AD=4,
∵OB'∥CF,且OA=OC,
∴AH=HE=AE=2,CE=2OH,
设,则.
在Rt中,,
解,得.
.
.
(1)由平行四边形的对角线互相平分得DO=BO,由轴对称性质得OB=OB',则OB'=OD,然后根据等边对等角可得结论;
(2)①由轴对称性质得AB=AB',∠BAC=∠B'AC=90°,则△ABC是等腰直角三角形,由等腰直角三角形的性质及勾股定理可得;由平行四边形的对边平行且相等可推出AB'∥CD,且AB'=CD,由一组对边平行且相等的四边形是平行四边形得出四边形ACDB'是平行四边形,进而根据平行四边形轴上计算方法可算出答案;
②过C作OB'的平行线,交AD、B'D分别于点E,F,由轴对称的性质及对顶角相等得∠AOB=∠AOB'=∠COD,由三角形的内角和定理及平角定义推出∠OB'D=∠AOB',由内错角相等两直线平行得AC∥B'D,由两组对边分别平行的四边形是平行四边形得四边形OCFB'是平行四边形,由平行四边形的对边相等得CF=OB',由二直线平行,内错角相等及等量代换得∠CAD=∠ADF=∠CAD,用ASA判断出△EDF≌△EDC,由全等三角形的对应边相等得EF=EC;由平行四边形性质得AB=CD=AC,AD=BC=8,OA=OC,有等腰三角形的三线合一得AE=DE=AD=4,由三角形的中位线定理得AH=HE=AE=2,CE=2OH,设OH=x,则CE=EF=2x,OD=OB'=CF=4x,在Rt△OHD中,利用勾股定理建立方程求出x的值,从而得出CE、HB'的长,最后根据三角形面积公式,由列式计算即可.
同课章节目录
