2024-2025学年八年级下学期数学期考末模拟卷(浙江温州市专用)【答案+解析】
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末模拟卷(浙江温州市专用)【答案+解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 457.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:34:17 | ||
图片预览


文档简介
保密★启用前
2024-2025学年八年级下册期末模拟卷(温州市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.推进生态文明建设,实行垃圾分类和资源化利用是每个公民义不容辞的责任.下列四幅图是垃圾分类标志图案,每幅图案下配有文字说明.则四幅图案中既是轴对称图形,又是中心对称图形的是( )
A.有害垃圾 B.可回收物
C.厨余垃圾 D.其他垃圾
2.在解一元二次方程时,小马同学粗心地将项的系数与常数项对换了,使得方程也变了.他正确地解出了这个不同的方程,得到一个根是2,另一根等于原方程的一个根.则原方程两根的平方和是( )
A. B. C. D.
3.已知点E,F分别在边长为3的正方形的边,上,且点F 为的三等分点,若平分,则的长为( )
A.或 B.或 C.或 D.或
4.甲、乙两名射击运动员在相同的条件下,各射击10次. 经计算:甲射击成绩的平均数是8环,且;乙射击成绩的平均数是8环,且.则下列说法中, 不一定正确的是( )
A.甲、乙射击的总环数相同 B.甲的成绩比乙的成绩稳定
C.乙的成绩比甲的成绩波动大 D.甲、乙两成绩的众数相同
5.若反比例函数的图象经过点,则下列结论中不正确的是( )
A.图象一定不经过 B.图象一定经过
C.图象一定经过 D.图象一定经过
6.下列一元二次方程中,有两个不相等的实数根的是( )
A. B.
C. D.
7.若用反证法证明命题“在中,若,则”,则应假设( )
A. B. C. D.
8.已知一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等,若ax2+bx+1=0的另一个根为4,则x2+bx+a=0的两个根分别为( )
A.﹣4,4 B.﹣4,1 C. D.
9.已知是整数,a是正整数,a的最小值是( )
A.0 B.3 C.6 D.24
10.如图,菱形ABCD中,点为对称中心,点从点出发沿AB向点移动,移动到点停止,作射线EO,交边CD于点,则四边形AECF形状的变化依次为( )
A.平行四边形正方形平行四边形矩形
B.平行四边形正方形矩形菱形
C.平行四边形矩形平行四边形菱形
D.平行四边形菱形正方形矩形
二、填空题(本题有6小题,每小题3分,共18分)
11.当 时,是整数.(写出一个符合条件的x的值)
12.若关于 的一元二次方程 的解为 , ,则关于 的一元二次方程 的解为 .
13.如图,四边形为平行四边形,延长到,使,连结,,,要使四边形成为矩形,可添加一个条件是 .(只要写出一个条件即可)
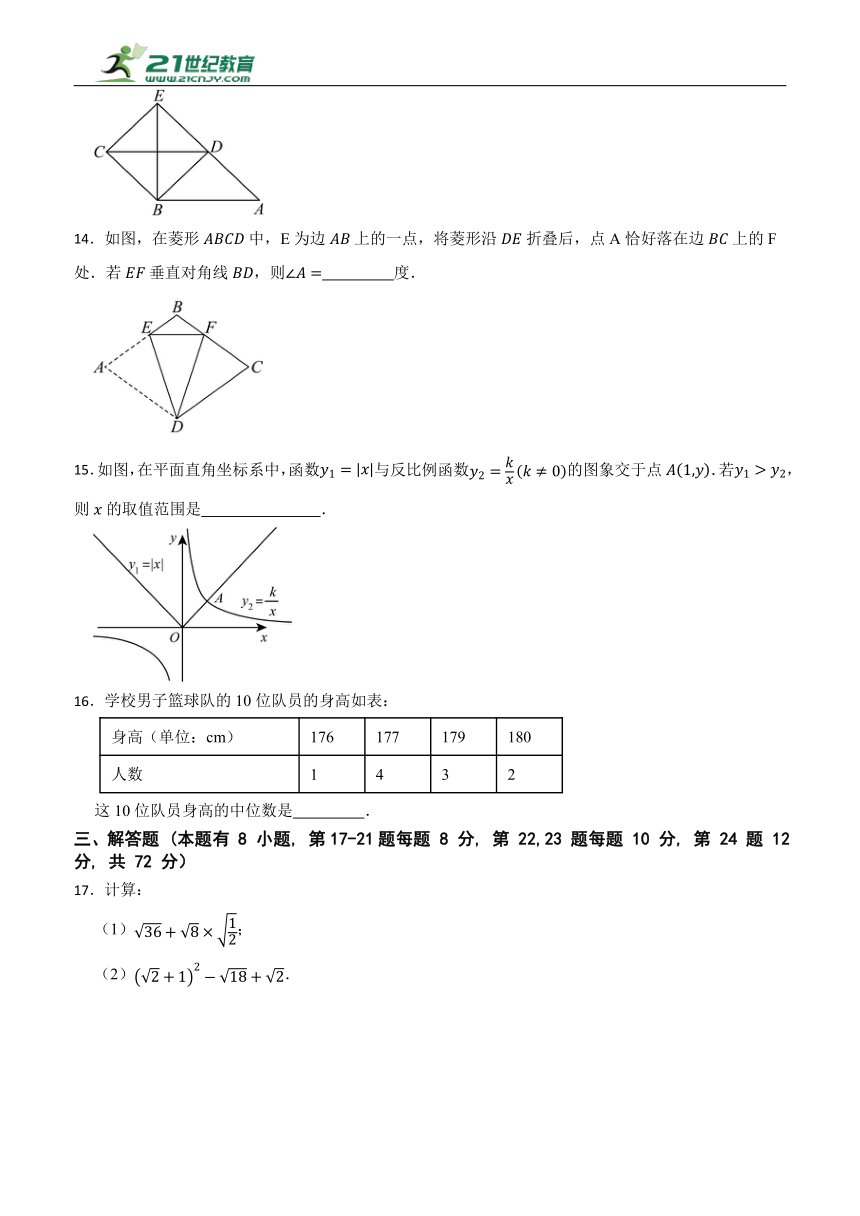
14.如图,在菱形中,E为边上的一点,将菱形沿折叠后,点A恰好落在边上的F处.若垂直对角线,则 度.
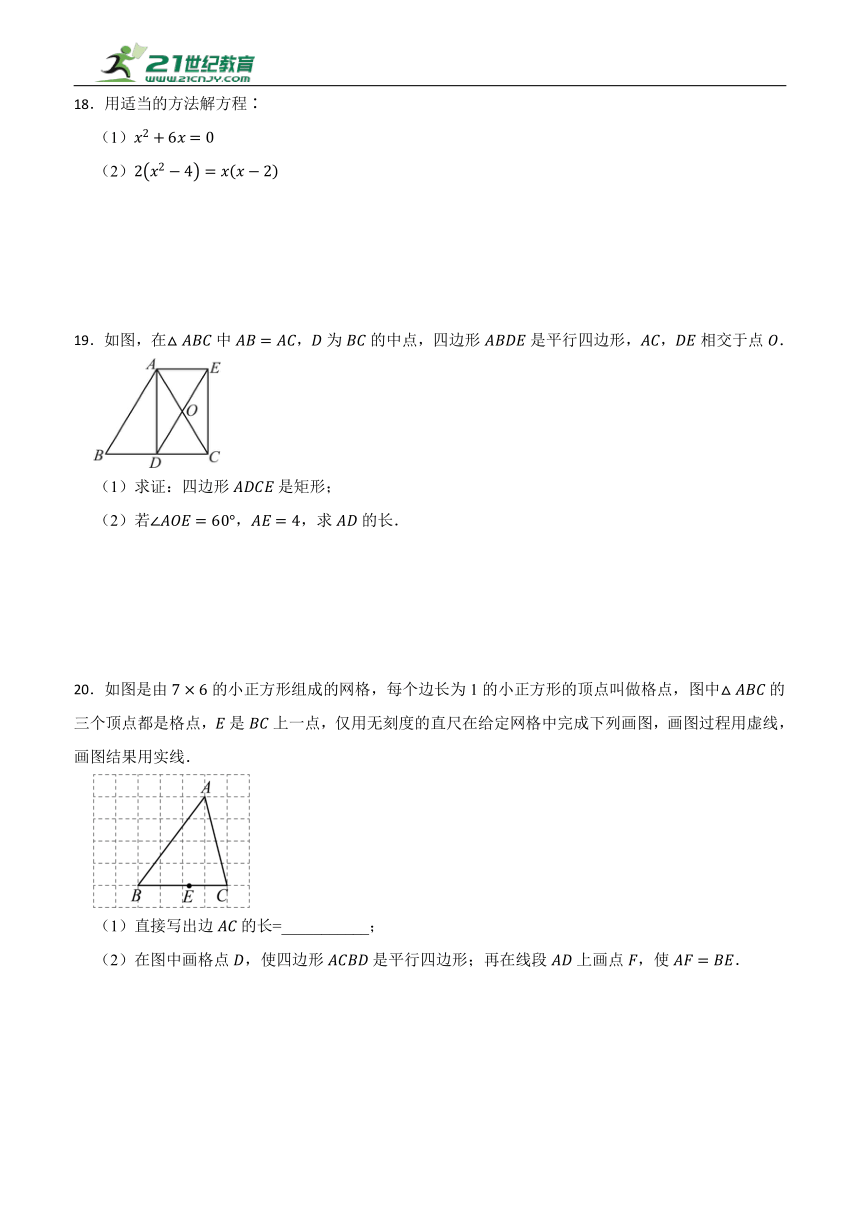
15.如图,在平面直角坐标系中,函数与反比例函数的图象交于点.若,则的取值范围是 .
16.学校男子篮球队的10位队员的身高如表:
身高(单位:cm) 176 177 179 180
人数 1 4 3 2
这10位队员身高的中位数是 .
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1);
(2).
18.用适当的方法解方程∶
(1)
(2)
19.如图,在中,为的中点,四边形是平行四边形,,相交于点.
(1)求证:四边形是矩形;
(2)若,,求的长.
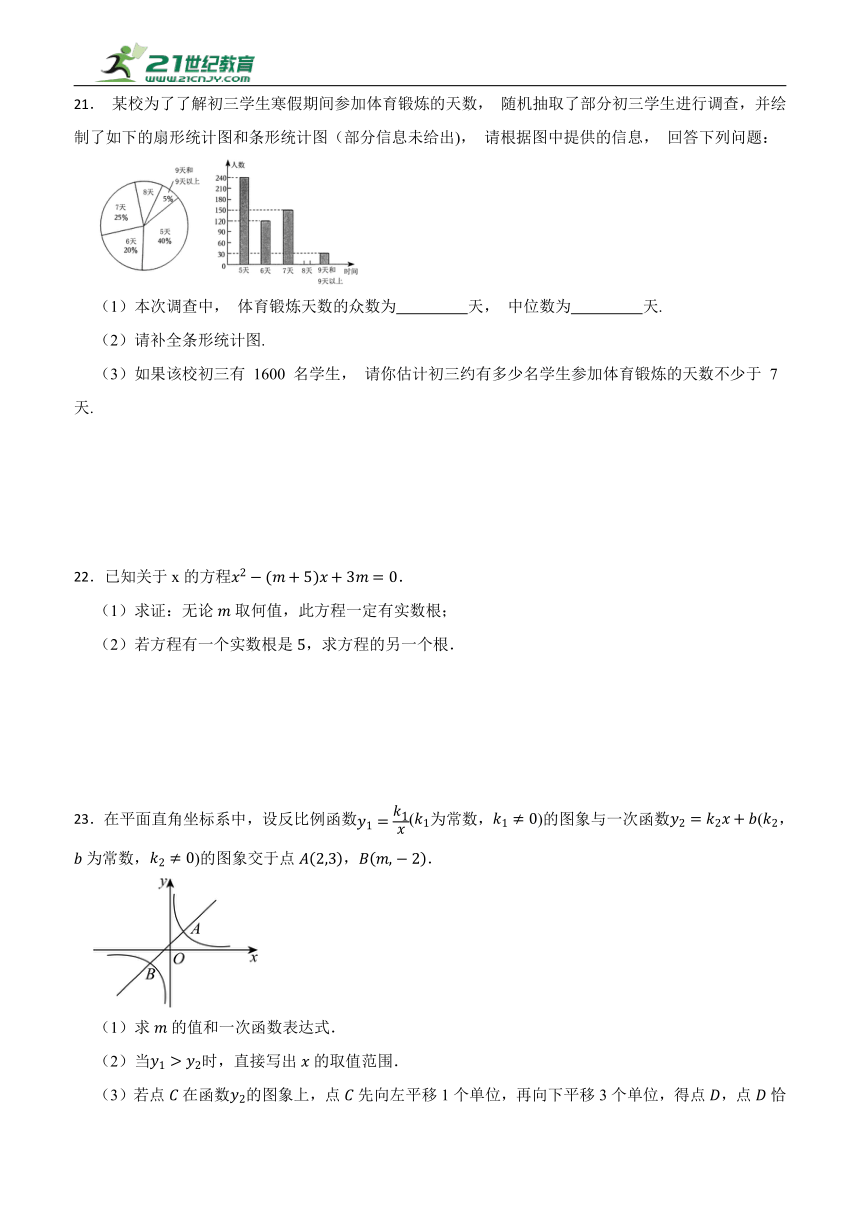
20.如图是由的小正方形组成的网格,每个边长为1的小正方形的顶点叫做格点,图中的三个顶点都是格点,是上一点,仅用无刻度的直尺在给定网格中完成下列画图,画图过程用虚线,画图结果用实线.
(1)直接写出边的长=___________;
(2)在图中画格点,使四边形是平行四边形;再在线段上画点,使.
21. 某校为了了解初三学生寒假期间参加体育锻炼的天数, 随机抽取了部分初三学生进行调查,并绘制了如下的扇形统计图和条形统计图(部分信息未给出), 请根据图中提供的信息, 回答下列问题:
(1)本次调查中, 体育锻炼天数的众数为 天, 中位数为 天.
(2)请补全条形统计图.
(3)如果该校初三有 1600 名学生, 请你估计初三约有多少名学生参加体育锻炼的天数不少于 7 天.
22.已知关于x的方程.
(1)求证:无论取何值,此方程一定有实数根;
(2)若方程有一个实数根是,求方程的另一个根.
23.在平面直角坐标系中,设反比例函数(为常数,)的图象与一次函数(,为常数,)的图象交于点,.
(1)求的值和一次函数表达式.
(2)当时,直接写出的取值范围.
(3)若点在函数的图象上,点先向左平移1个单位,再向下平移3个单位,得点,点恰好落在函数的图象上,求点的坐标.
24.如图1,,过点D作交于点E,连接.
(1)求证:四边形是菱形.
(2)若,,E为的中点.
①求的长.
②如图2,在边上取一点F,连结并延长交的延长线于点G,记的面积为,的面积为,当时,求的长.
答案解析部分
1.A
解:A、既是轴对称图形也是中心对称图形,故A选项符合题意;
B、不是轴对称图形也不是中心对称图形,故B选项不符合题意;
C、是轴对称图形而不是中心对称图形,故C选项不符合题意;
D、不是中心对称图形也不是轴对称图形,故D选项不符合题意;
故答案为:A.
根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,据此判断即可.
2.D
解:设原方程为,两个根为和;则新的方程为,两个根为2和.
∴,,
得,
∵两个方程不同,
∴a≠c,
∴,
∴,
∴.
①当时,代入新方程可得:,
解得:,
则,,
则.
②当时,代入新方程可得:,
解得:,
则,,
则.
综上,原方程两根的平方和是.
故答案为:D.
设原方程为,两个根为和.则新的方程为,两个根为2和.把根代入方程可得,,将①②联立可解得.分别把β=1和β=﹣1代入新方程,得到a、b、c之间的关系,再由根与系数的关系可求出与的值,进而可求出的值.
3.A
解:∵四边形是正方形,
,,
∵平分,
∴∠AEF=∠GEF.
延长EA到点G,使EG=EF,如图所示:
又∵∠AEF=∠GEF,BE=BE,
∴△GBE≌△FBE(SAS),
∴BG=BF.
又∵∠GAB=∠EAB=∠C=90°,
AB=CB,
∴△GAB≌△FCB(HL),
∴AG=CF.
设,则,
∵F为线段CD的三等分点,
①当时,,AG=CF=1.
∴,
在中,由得,
,
解得,
;
②当时,,AG=CF=2.
∴,
由得,
,
解得
.
综上,的长为或.
故答案为:A.
延长EA到点G,使EG=EF,结合正方形的性质可角平分线的定义,可利用SAS证明△GBE≌△FBE,进而再利用证明△GAB≌△FCB,可得AG=CF.设,则,EF=EG=AG+x.然后分两种情况讨论:①当时,②当时两种情况,在中利用勾股定理列方程求出x的值即可.
4.D
解:由题意:甲和射击成绩的平均数都是8环,
∴甲的总环数=乙的总环数=8×10=80(环)
∴甲、乙的总环数相同,故选项A正确,不符合题意;
∵,,
.
∴甲的成绩比乙的成绩稳定,而乙的成绩比甲的成绩波动大,故选项B和选项C都正确,不符合题意;
∵不知道甲和乙两人10次射击的具体值,
∴不能得到甲、乙成绩的众数相同,故选项D不一定正确,符合题意;
故答案为:D.
根据平均数可计算总总环数,可判断选项A;方差用来衡量一组数据的波动大小,方差越大,波动越大,数据越不稳定;反之方差越小,波动越小,数据越稳定,据此可判断选项B,C;根据10次成绩的具体值的知否情况,可判断选项D.
5.C
解:A、反比例函数的图象与坐标轴没有交点,
图象一定不经过,此选项不合题意;
B、反比例函数的图象经过点,
,
,
当时,则,
图象一定经过,此选项不符合题意;
C、把代入,得,此选项符合题意;
D、把代入,得,图象一定经过,此选项不符合题意.
故答案为:C.
把各选项中的点的坐标代入反比例函数的解析式计算,然后根据计算结果和反比例函数图象上点的坐标特征即可判断求解.
6.C
解:A、∵a=1,b=-2,c=3,
∴,
方程没有实数根,此选项不符合题意;
B、∵a=1,b=6,c=9,
∴,
方程有两个相等的实数根,此选项不符合题意;
C、∵a=4,b=-3,c=-2,
∴,
方程有两个不相等的实数根,此选项符合题意;
D、∵a=3,b=-1,c=2,
∴,
方程没有实数根,此选项不符合题意.
故答案为:C.
由题意分别求出每个方程中判别式b2-4ac的值,再根据一元二次方程的根的判别式"①当b2-4ac>0时,方程有两个不相等的实数根;②当b2-4ac=0时,方程有两个相等的实数根;③当b2-4ac<0时,方程没有实数根"可判断求解.
7.B
解:由题意,应假设,
故答案为:B.
根据反证法的步骤中,第一步是假设结论不成立,从而推出与已知条件(或已学过的性质等)相矛盾的结论,于是可得原假设不成立,原命题得证.
8.D
解:∵一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等,
∴ax2+bx+1=x2+bx+a,
解得x2=1,
∴正根为1,
∵ax2+bx+1=0的另一个根为4,
∴,
∴,
∵方程x2+bx+a=0有一个正根为1,设另一个根为m,
∴则1×m=a=,
∴m=,
∴另一个根为,
∴x2+bx+a=0的两个根分别为1,.
故选:D.
先根据“一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等”求出方程的正根,再求出,再结合“方程x2+bx+a=0有一个正根为1”设另一个根为m,利用根与系数的关系可得1×m=a=,求出m的值即可.
9.C
解:∵,且是整数,
∴是整数,即6a是完全平方数;
∴a的最小正整数值为6.
故选C.
因为是整数,且,则6a是完全平方数,满足条件的最小正整数a为6.
10.C
解:∵平行四边形ABCD是菱形,点O为对称中心,
∴这个四边形开始是平行四边形,当对角线相等时是矩形,然后是平行四边形,最后点E与点B重合时是菱形.
故答案为:C.
根据中心对称的定义“在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形”并结合菱形的性质、矩形的判定、平行四边形的判定即可得四边形AECF的形状的变化情况.
11.1
解:若二次根式有意义,
则,
解得:,
∵是整数,
∴10-x是一个完全平方数,
∴x可以等于1,当x=1时,是整数.
故答案为:1(答案不唯一).
首先根据二次根式的被开方数不能为负数列出不等式得出x的取值范围,再根据该二次根式的值是整数,可得10-x是一个完全平方数,据此在x的取值范围内取值求解即可.
12. ,
解:令
则方程 可变形为
由题意得:关于t的方程 的解为 ,
即 ,
解得 ,
则关于 的一元二次方程 的解为 ,
故答案为: , .
将y+1看着整体,结合两方程的特点可得y+1=1,y+1=2,然后可求出y的值。
13.(或或等)
解:四边形为平行四边形,
,,
又,
,且,
四边形为平行四边形,
添加,
为矩形;
添加,
,
为矩形;
添加,
,
为矩形.
故答案为:(或或)
由于BC与DE平行且相等,因此四边形BDEC是平行四边形;则BE=CD=BA时,平行四边形BDEC是矩形;时,平行四边形BDEC是矩形.
14.
解:连接,
四边形是菱形,
,,
设,
垂直对角线,
,
,
由折叠的性质知,
,
,
,
,
解得,
,
故答案为:72.
由菱形的性质得到,并得到,根据平行线的性质及折叠的性质得出角的关系,由平角的定义列出等式解方程即可解答.
15.或
解:由图可知:当或时.
故答案为:或.
y1>y2,就是y1的图象高于y2的图象所对应的x的范围,观察函数图象并结合两图象的交点A的坐标即可求解.
16.178
解:∵学校男子篮球队有10位队员,∴第五、第六位队员的身高的平均数就是这组数据的中位数,
而第五、第六位队员的身高分别是177,179,
位队员身高的中位数是,
故答案为:178.
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.根据中位数的定义并结合统计表中的数据计算即可求解.
17.(1)解:
;
(2)解:
.
(1)先根据二次根式的乘法法则“”计算二次根式的乘法,再根据二次根式的性质“”化简二次根式,最后计算加法即可;
(2)先根据完全平方公式展开括号,同时根据二次根式化简二次根式,最后合并同类二次根式及进行有理数的加减法运算即可.
(1)解:
;
(2)解:
.
18.(1)解:,
,
或,
,;
(2)解:,
,
,
,
或,
,.
(1)此题缺常数项,用因式分解法求解较为简单,首先将方程的左边利用提取公因式法分解因式,然后根据两个因式的乘积等于零,则至少有一个因式为零,从而将方程将次为两个一元一次方程,解两个一元一次方程即可;
(2)先将方程的左边利用平方差公式分解因式,然后把x-2看成一个整体,此题缺常数项,用因式分解法求解较为简单,然后将方程右边整体移到方程左边,将方程的左边利用提取公因式法分解因式,然后根据两个因式的乘积等于零,则至少有一个因式为零,从而将方程将次为两个一元一次方程,解两个一元一次方程即可.
19.(1)证明:∵四边形是平行四边形,∴,,
∵为中点,
∴,
∴四边形是平行四边形,
∵,为中点,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,∴,,
∵,,
∴是等边三角形,
∴,
∴,
∵,
∴.
()利用平行四边形的性质得到,,即可得到是平行四边形,再证明,即可得到结论;
()先证明为等边三角形,求出的长,即可得到矩形对角线的长,再根据勾股定理解题.
(1)证明:∵四边形是平行四边形,
∴,,
∵为中点,
∴,
∴四边形是平行四边形,
∵,为中点,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,
∴,,
∵,,
∴是等边三角形,
∴,
∴,
∵,
∴.
20.(1)
(2)解:如图所示,即为所求;
(1)
解:根据勾股定理可得:,
故答案为:.
本题考查了勾股定理,平行四边形的性质,格点作图.
(1)根据勾股定理即可求解;
(2)由于平行四边形的对边平行且相等,可确定格点D并使BD与AC平行且相等,再分别连接AD、BD即可;由于平行四边形是中心对称图形,因此可连接交AB于一点O,再过点E作射线EO交AD于点F即可.
(1)解:根据勾股定理可得:,
故答案为:.
(2)解:如图所示,即为所求;
21.(1)5;6
(2)解:锻炼8天的人数:600-240-120-150-30=60(人)
再补全条形统计图,如下:
(3)解:
(人)
∴初三体育锻炼不少于 7 天的有640人.
解:(1)由图可知:锻炼5天的有240人,
∴众数为5
∵30÷5%=600(人)
第300个数据,301个数据分别为:6,6
∴中位数为6
故答案为:5,6.
(1)众数是一组数据中出现次数最多的数,而5出现的次数最多;把这组数据排序后,则它的中位数是中间位置的两个数的平均数
(2)先用总人数减去其他各项的人数,得出锻炼8天的人数,再补全统计图即可
(3)先计算出 参加体育锻炼的天数不少于 7 天 的百分率,再乘以1600即可.
22.(1)证明:由已知可得:a=1,b=-(m+5),c=3m,
∴,
∵(m-1)2≥0
∴(m-1)2+24≥0
∴无论取何值,此方程一定有实数根.
(2)解: ∵方程 有一个实数根是5,
∴当时,原方程=,
解得:,
∴将m=0代入原方程,得,
解得:,,
∴该方程的另一个根为.
23.(1)解:将点坐标代入反比例函数解析式得,
,
所以反比例函数的解析式为.
将点坐标代入反比例函数解析式得,
,
所以点的坐标为.
将,两点坐标代入一次函数解析式得,
,
解得,
所以一次函数的解析式为.
(2)解:由函数图象可知,当或时,反比例函数的图象在一次函数图象的上方,即,
所以当时,的取值范围是:或.
(3)解:因为点在函数的图象上,
所以令点的坐标为,
则点向左平移个单位,再向下平移个单位后,所得点的坐标可表示为,
即点的坐标为.
因为点在函数的图象上,
所以,
解得,
所以点的坐标为或.
(1)先根据待定系数法求出反比例函数的解析式,再将点坐标代入反比例函数解析式,求出m的值,最后根据待定系数法求出一次函数的解析式即可;
(2)结合函数图象以及,两点坐标,即可求解;
(3)设点的坐标为,根据平移的方向的单位可得点的坐标,最后将点坐标代入反比例函数的解析式,求出m的值,即可求解.
(1)解:将点坐标代入反比例函数解析式得,
,
所以反比例函数的解析式为.
将点坐标代入反比例函数解析式得,
,
所以点的坐标为.
将,两点坐标代入一次函数解析式得,
,
解得,
所以一次函数的解析式为.
(2)由函数图象可知,
当或时,反比例函数的图象在一次函数图象的上方,即,
所以当时,的取值范围是:或.
(3)因为点在函数的图象上,
所以令点的坐标为,
则点向左平移个单位,再向下平移个单位后,所得点的坐标可表示为,
即点的坐标为.
因为点在函数的图象上,
所以,
解得,
所以点的坐标为或.
24.(1)证明: ,
,,
,
,
,
,
,
四边形是平行四边形,
∵,
四边形是菱形.
(2)解:① 连接交于点,
四边形是菱形,
,,,
设,
则,
E为的中点,
,
在,,
在,,
,
解得,
.
② 过点作于点,如图所示,
前面已证得四边形是菱形,
,,,
∵E为的中点,
∴,
∴,
,
,
∴,解得: .
,,,
,
,
,
,
,
解得:.
所以.
(1)先根据全等三角形的性质,得出,,再利用平行线的性质得到,从而可得到,再根据等角对等边,得到,从而可得,可证得四边形是平行四边形,再结合一组邻边相等即可证得四边形是菱形;
(2)① 先根据菱形性质,得到,,,再设,可用a表示出CE与AE,再利用勾股定理求解;
②先利用勾股定理求得BD,再利用等面积法得,到关于DM的方程求解求得DM,然后利用,,,得到,代入后转化关于BG的方程求解.
(1)证明: ,
,,
,
,
,
,
,且,
四边形是平行四边形,
又,
四边形是菱形.
(2)解:① 连接交于点,
四边形是菱形,
,,,
设,则,
E为的中点,
,
在,,
在,,
,
解得,
.
② 过点作于点,如图所示,
前面已证得四边形是菱形,,,又E为的中点,
,,,
,
,即,
.
,,,
,
,
,,
,
解得.
故.
2024-2025学年八年级下册期末模拟卷(温州市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.推进生态文明建设,实行垃圾分类和资源化利用是每个公民义不容辞的责任.下列四幅图是垃圾分类标志图案,每幅图案下配有文字说明.则四幅图案中既是轴对称图形,又是中心对称图形的是( )
A.有害垃圾 B.可回收物
C.厨余垃圾 D.其他垃圾
2.在解一元二次方程时,小马同学粗心地将项的系数与常数项对换了,使得方程也变了.他正确地解出了这个不同的方程,得到一个根是2,另一根等于原方程的一个根.则原方程两根的平方和是( )
A. B. C. D.
3.已知点E,F分别在边长为3的正方形的边,上,且点F 为的三等分点,若平分,则的长为( )
A.或 B.或 C.或 D.或
4.甲、乙两名射击运动员在相同的条件下,各射击10次. 经计算:甲射击成绩的平均数是8环,且;乙射击成绩的平均数是8环,且.则下列说法中, 不一定正确的是( )
A.甲、乙射击的总环数相同 B.甲的成绩比乙的成绩稳定
C.乙的成绩比甲的成绩波动大 D.甲、乙两成绩的众数相同
5.若反比例函数的图象经过点,则下列结论中不正确的是( )
A.图象一定不经过 B.图象一定经过
C.图象一定经过 D.图象一定经过
6.下列一元二次方程中,有两个不相等的实数根的是( )
A. B.
C. D.
7.若用反证法证明命题“在中,若,则”,则应假设( )
A. B. C. D.
8.已知一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等,若ax2+bx+1=0的另一个根为4,则x2+bx+a=0的两个根分别为( )
A.﹣4,4 B.﹣4,1 C. D.
9.已知是整数,a是正整数,a的最小值是( )
A.0 B.3 C.6 D.24
10.如图,菱形ABCD中,点为对称中心,点从点出发沿AB向点移动,移动到点停止,作射线EO,交边CD于点,则四边形AECF形状的变化依次为( )
A.平行四边形正方形平行四边形矩形
B.平行四边形正方形矩形菱形
C.平行四边形矩形平行四边形菱形
D.平行四边形菱形正方形矩形
二、填空题(本题有6小题,每小题3分,共18分)
11.当 时,是整数.(写出一个符合条件的x的值)
12.若关于 的一元二次方程 的解为 , ,则关于 的一元二次方程 的解为 .
13.如图,四边形为平行四边形,延长到,使,连结,,,要使四边形成为矩形,可添加一个条件是 .(只要写出一个条件即可)
14.如图,在菱形中,E为边上的一点,将菱形沿折叠后,点A恰好落在边上的F处.若垂直对角线,则 度.
15.如图,在平面直角坐标系中,函数与反比例函数的图象交于点.若,则的取值范围是 .
16.学校男子篮球队的10位队员的身高如表:
身高(单位:cm) 176 177 179 180
人数 1 4 3 2
这10位队员身高的中位数是 .
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1);
(2).
18.用适当的方法解方程∶
(1)
(2)
19.如图,在中,为的中点,四边形是平行四边形,,相交于点.
(1)求证:四边形是矩形;
(2)若,,求的长.
20.如图是由的小正方形组成的网格,每个边长为1的小正方形的顶点叫做格点,图中的三个顶点都是格点,是上一点,仅用无刻度的直尺在给定网格中完成下列画图,画图过程用虚线,画图结果用实线.
(1)直接写出边的长=___________;
(2)在图中画格点,使四边形是平行四边形;再在线段上画点,使.
21. 某校为了了解初三学生寒假期间参加体育锻炼的天数, 随机抽取了部分初三学生进行调查,并绘制了如下的扇形统计图和条形统计图(部分信息未给出), 请根据图中提供的信息, 回答下列问题:
(1)本次调查中, 体育锻炼天数的众数为 天, 中位数为 天.
(2)请补全条形统计图.
(3)如果该校初三有 1600 名学生, 请你估计初三约有多少名学生参加体育锻炼的天数不少于 7 天.
22.已知关于x的方程.
(1)求证:无论取何值,此方程一定有实数根;
(2)若方程有一个实数根是,求方程的另一个根.
23.在平面直角坐标系中,设反比例函数(为常数,)的图象与一次函数(,为常数,)的图象交于点,.
(1)求的值和一次函数表达式.
(2)当时,直接写出的取值范围.
(3)若点在函数的图象上,点先向左平移1个单位,再向下平移3个单位,得点,点恰好落在函数的图象上,求点的坐标.
24.如图1,,过点D作交于点E,连接.
(1)求证:四边形是菱形.
(2)若,,E为的中点.
①求的长.
②如图2,在边上取一点F,连结并延长交的延长线于点G,记的面积为,的面积为,当时,求的长.
答案解析部分
1.A
解:A、既是轴对称图形也是中心对称图形,故A选项符合题意;
B、不是轴对称图形也不是中心对称图形,故B选项不符合题意;
C、是轴对称图形而不是中心对称图形,故C选项不符合题意;
D、不是中心对称图形也不是轴对称图形,故D选项不符合题意;
故答案为:A.
根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,据此判断即可.
2.D
解:设原方程为,两个根为和;则新的方程为,两个根为2和.
∴,,
得,
∵两个方程不同,
∴a≠c,
∴,
∴,
∴.
①当时,代入新方程可得:,
解得:,
则,,
则.
②当时,代入新方程可得:,
解得:,
则,,
则.
综上,原方程两根的平方和是.
故答案为:D.
设原方程为,两个根为和.则新的方程为,两个根为2和.把根代入方程可得,,将①②联立可解得.分别把β=1和β=﹣1代入新方程,得到a、b、c之间的关系,再由根与系数的关系可求出与的值,进而可求出的值.
3.A
解:∵四边形是正方形,
,,
∵平分,
∴∠AEF=∠GEF.
延长EA到点G,使EG=EF,如图所示:
又∵∠AEF=∠GEF,BE=BE,
∴△GBE≌△FBE(SAS),
∴BG=BF.
又∵∠GAB=∠EAB=∠C=90°,
AB=CB,
∴△GAB≌△FCB(HL),
∴AG=CF.
设,则,
∵F为线段CD的三等分点,
①当时,,AG=CF=1.
∴,
在中,由得,
,
解得,
;
②当时,,AG=CF=2.
∴,
由得,
,
解得
.
综上,的长为或.
故答案为:A.
延长EA到点G,使EG=EF,结合正方形的性质可角平分线的定义,可利用SAS证明△GBE≌△FBE,进而再利用证明△GAB≌△FCB,可得AG=CF.设,则,EF=EG=AG+x.然后分两种情况讨论:①当时,②当时两种情况,在中利用勾股定理列方程求出x的值即可.
4.D
解:由题意:甲和射击成绩的平均数都是8环,
∴甲的总环数=乙的总环数=8×10=80(环)
∴甲、乙的总环数相同,故选项A正确,不符合题意;
∵,,
.
∴甲的成绩比乙的成绩稳定,而乙的成绩比甲的成绩波动大,故选项B和选项C都正确,不符合题意;
∵不知道甲和乙两人10次射击的具体值,
∴不能得到甲、乙成绩的众数相同,故选项D不一定正确,符合题意;
故答案为:D.
根据平均数可计算总总环数,可判断选项A;方差用来衡量一组数据的波动大小,方差越大,波动越大,数据越不稳定;反之方差越小,波动越小,数据越稳定,据此可判断选项B,C;根据10次成绩的具体值的知否情况,可判断选项D.
5.C
解:A、反比例函数的图象与坐标轴没有交点,
图象一定不经过,此选项不合题意;
B、反比例函数的图象经过点,
,
,
当时,则,
图象一定经过,此选项不符合题意;
C、把代入,得,此选项符合题意;
D、把代入,得,图象一定经过,此选项不符合题意.
故答案为:C.
把各选项中的点的坐标代入反比例函数的解析式计算,然后根据计算结果和反比例函数图象上点的坐标特征即可判断求解.
6.C
解:A、∵a=1,b=-2,c=3,
∴,
方程没有实数根,此选项不符合题意;
B、∵a=1,b=6,c=9,
∴,
方程有两个相等的实数根,此选项不符合题意;
C、∵a=4,b=-3,c=-2,
∴,
方程有两个不相等的实数根,此选项符合题意;
D、∵a=3,b=-1,c=2,
∴,
方程没有实数根,此选项不符合题意.
故答案为:C.
由题意分别求出每个方程中判别式b2-4ac的值,再根据一元二次方程的根的判别式"①当b2-4ac>0时,方程有两个不相等的实数根;②当b2-4ac=0时,方程有两个相等的实数根;③当b2-4ac<0时,方程没有实数根"可判断求解.
7.B
解:由题意,应假设,
故答案为:B.
根据反证法的步骤中,第一步是假设结论不成立,从而推出与已知条件(或已学过的性质等)相矛盾的结论,于是可得原假设不成立,原命题得证.
8.D
解:∵一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等,
∴ax2+bx+1=x2+bx+a,
解得x2=1,
∴正根为1,
∵ax2+bx+1=0的另一个根为4,
∴,
∴,
∵方程x2+bx+a=0有一个正根为1,设另一个根为m,
∴则1×m=a=,
∴m=,
∴另一个根为,
∴x2+bx+a=0的两个根分别为1,.
故选:D.
先根据“一元二次方程ax2+bx+1=0(a≠0)的一个正根和方程x2+bx+a=0的一个正根相等”求出方程的正根,再求出,再结合“方程x2+bx+a=0有一个正根为1”设另一个根为m,利用根与系数的关系可得1×m=a=,求出m的值即可.
9.C
解:∵,且是整数,
∴是整数,即6a是完全平方数;
∴a的最小正整数值为6.
故选C.
因为是整数,且,则6a是完全平方数,满足条件的最小正整数a为6.
10.C
解:∵平行四边形ABCD是菱形,点O为对称中心,
∴这个四边形开始是平行四边形,当对角线相等时是矩形,然后是平行四边形,最后点E与点B重合时是菱形.
故答案为:C.
根据中心对称的定义“在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形”并结合菱形的性质、矩形的判定、平行四边形的判定即可得四边形AECF的形状的变化情况.
11.1
解:若二次根式有意义,
则,
解得:,
∵是整数,
∴10-x是一个完全平方数,
∴x可以等于1,当x=1时,是整数.
故答案为:1(答案不唯一).
首先根据二次根式的被开方数不能为负数列出不等式得出x的取值范围,再根据该二次根式的值是整数,可得10-x是一个完全平方数,据此在x的取值范围内取值求解即可.
12. ,
解:令
则方程 可变形为
由题意得:关于t的方程 的解为 ,
即 ,
解得 ,
则关于 的一元二次方程 的解为 ,
故答案为: , .
将y+1看着整体,结合两方程的特点可得y+1=1,y+1=2,然后可求出y的值。
13.(或或等)
解:四边形为平行四边形,
,,
又,
,且,
四边形为平行四边形,
添加,
为矩形;
添加,
,
为矩形;
添加,
,
为矩形.
故答案为:(或或)
由于BC与DE平行且相等,因此四边形BDEC是平行四边形;则BE=CD=BA时,平行四边形BDEC是矩形;时,平行四边形BDEC是矩形.
14.
解:连接,
四边形是菱形,
,,
设,
垂直对角线,
,
,
由折叠的性质知,
,
,
,
,
解得,
,
故答案为:72.
由菱形的性质得到,并得到,根据平行线的性质及折叠的性质得出角的关系,由平角的定义列出等式解方程即可解答.
15.或
解:由图可知:当或时.
故答案为:或.
y1>y2,就是y1的图象高于y2的图象所对应的x的范围,观察函数图象并结合两图象的交点A的坐标即可求解.
16.178
解:∵学校男子篮球队有10位队员,∴第五、第六位队员的身高的平均数就是这组数据的中位数,
而第五、第六位队员的身高分别是177,179,
位队员身高的中位数是,
故答案为:178.
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.根据中位数的定义并结合统计表中的数据计算即可求解.
17.(1)解:
;
(2)解:
.
(1)先根据二次根式的乘法法则“”计算二次根式的乘法,再根据二次根式的性质“”化简二次根式,最后计算加法即可;
(2)先根据完全平方公式展开括号,同时根据二次根式化简二次根式,最后合并同类二次根式及进行有理数的加减法运算即可.
(1)解:
;
(2)解:
.
18.(1)解:,
,
或,
,;
(2)解:,
,
,
,
或,
,.
(1)此题缺常数项,用因式分解法求解较为简单,首先将方程的左边利用提取公因式法分解因式,然后根据两个因式的乘积等于零,则至少有一个因式为零,从而将方程将次为两个一元一次方程,解两个一元一次方程即可;
(2)先将方程的左边利用平方差公式分解因式,然后把x-2看成一个整体,此题缺常数项,用因式分解法求解较为简单,然后将方程右边整体移到方程左边,将方程的左边利用提取公因式法分解因式,然后根据两个因式的乘积等于零,则至少有一个因式为零,从而将方程将次为两个一元一次方程,解两个一元一次方程即可.
19.(1)证明:∵四边形是平行四边形,∴,,
∵为中点,
∴,
∴四边形是平行四边形,
∵,为中点,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,∴,,
∵,,
∴是等边三角形,
∴,
∴,
∵,
∴.
()利用平行四边形的性质得到,,即可得到是平行四边形,再证明,即可得到结论;
()先证明为等边三角形,求出的长,即可得到矩形对角线的长,再根据勾股定理解题.
(1)证明:∵四边形是平行四边形,
∴,,
∵为中点,
∴,
∴四边形是平行四边形,
∵,为中点,
∴,
∴,
∴平行四边形是矩形;
(2)解:∵四边形是矩形,
∴,,
∵,,
∴是等边三角形,
∴,
∴,
∵,
∴.
20.(1)
(2)解:如图所示,即为所求;
(1)
解:根据勾股定理可得:,
故答案为:.
本题考查了勾股定理,平行四边形的性质,格点作图.
(1)根据勾股定理即可求解;
(2)由于平行四边形的对边平行且相等,可确定格点D并使BD与AC平行且相等,再分别连接AD、BD即可;由于平行四边形是中心对称图形,因此可连接交AB于一点O,再过点E作射线EO交AD于点F即可.
(1)解:根据勾股定理可得:,
故答案为:.
(2)解:如图所示,即为所求;
21.(1)5;6
(2)解:锻炼8天的人数:600-240-120-150-30=60(人)
再补全条形统计图,如下:
(3)解:
(人)
∴初三体育锻炼不少于 7 天的有640人.
解:(1)由图可知:锻炼5天的有240人,
∴众数为5
∵30÷5%=600(人)
第300个数据,301个数据分别为:6,6
∴中位数为6
故答案为:5,6.
(1)众数是一组数据中出现次数最多的数,而5出现的次数最多;把这组数据排序后,则它的中位数是中间位置的两个数的平均数
(2)先用总人数减去其他各项的人数,得出锻炼8天的人数,再补全统计图即可
(3)先计算出 参加体育锻炼的天数不少于 7 天 的百分率,再乘以1600即可.
22.(1)证明:由已知可得:a=1,b=-(m+5),c=3m,
∴,
∵(m-1)2≥0
∴(m-1)2+24≥0
∴无论取何值,此方程一定有实数根.
(2)解: ∵方程 有一个实数根是5,
∴当时,原方程=,
解得:,
∴将m=0代入原方程,得,
解得:,,
∴该方程的另一个根为.
23.(1)解:将点坐标代入反比例函数解析式得,
,
所以反比例函数的解析式为.
将点坐标代入反比例函数解析式得,
,
所以点的坐标为.
将,两点坐标代入一次函数解析式得,
,
解得,
所以一次函数的解析式为.
(2)解:由函数图象可知,当或时,反比例函数的图象在一次函数图象的上方,即,
所以当时,的取值范围是:或.
(3)解:因为点在函数的图象上,
所以令点的坐标为,
则点向左平移个单位,再向下平移个单位后,所得点的坐标可表示为,
即点的坐标为.
因为点在函数的图象上,
所以,
解得,
所以点的坐标为或.
(1)先根据待定系数法求出反比例函数的解析式,再将点坐标代入反比例函数解析式,求出m的值,最后根据待定系数法求出一次函数的解析式即可;
(2)结合函数图象以及,两点坐标,即可求解;
(3)设点的坐标为,根据平移的方向的单位可得点的坐标,最后将点坐标代入反比例函数的解析式,求出m的值,即可求解.
(1)解:将点坐标代入反比例函数解析式得,
,
所以反比例函数的解析式为.
将点坐标代入反比例函数解析式得,
,
所以点的坐标为.
将,两点坐标代入一次函数解析式得,
,
解得,
所以一次函数的解析式为.
(2)由函数图象可知,
当或时,反比例函数的图象在一次函数图象的上方,即,
所以当时,的取值范围是:或.
(3)因为点在函数的图象上,
所以令点的坐标为,
则点向左平移个单位,再向下平移个单位后,所得点的坐标可表示为,
即点的坐标为.
因为点在函数的图象上,
所以,
解得,
所以点的坐标为或.
24.(1)证明: ,
,,
,
,
,
,
,
四边形是平行四边形,
∵,
四边形是菱形.
(2)解:① 连接交于点,
四边形是菱形,
,,,
设,
则,
E为的中点,
,
在,,
在,,
,
解得,
.
② 过点作于点,如图所示,
前面已证得四边形是菱形,
,,,
∵E为的中点,
∴,
∴,
,
,
∴,解得: .
,,,
,
,
,
,
,
解得:.
所以.
(1)先根据全等三角形的性质,得出,,再利用平行线的性质得到,从而可得到,再根据等角对等边,得到,从而可得,可证得四边形是平行四边形,再结合一组邻边相等即可证得四边形是菱形;
(2)① 先根据菱形性质,得到,,,再设,可用a表示出CE与AE,再利用勾股定理求解;
②先利用勾股定理求得BD,再利用等面积法得,到关于DM的方程求解求得DM,然后利用,,,得到,代入后转化关于BG的方程求解.
(1)证明: ,
,,
,
,
,
,
,且,
四边形是平行四边形,
又,
四边形是菱形.
(2)解:① 连接交于点,
四边形是菱形,
,,,
设,则,
E为的中点,
,
在,,
在,,
,
解得,
.
② 过点作于点,如图所示,
前面已证得四边形是菱形,,,又E为的中点,
,,,
,
,即,
.
,,,
,
,
,,
,
解得.
故.
同课章节目录
