2024-2025学年八年级下学期数学期考末模拟卷(浙江义乌市专用) 【答案+解析】
文档属性
| 名称 | 2024-2025学年八年级下学期数学期考末模拟卷(浙江义乌市专用) 【答案+解析】 |  | |
| 格式 | docx | ||
| 文件大小 | 328.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:14:12 | ||
图片预览



文档简介
保密★启用前
2024-2025学年八年级下册期末模拟卷(义乌市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.下列属于一元二次方程的是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,在矩形中,点A、B在y轴上,轴,对角线交于点E,,,反比例函数经过C、E两点,则k的值为( )
A.7 B.8 C.9 D.10
5.两张全等的矩形纸片,按如图所示的方式交叉叠放,,,与交于点G,与交于点H.若,,则四边形的面积为( )
A.4 B. C.8 D.16
6.用反证法证明命题“在中,,求证:”,应先假设( )
A. B. C. D.
7.已知5个均不相等的正数a1,a2,7,a3,a4的平均数为7,方差为,而a1,a2,a3,a4,这四个数的方差,则下列正确的是
A. B. C. D.
8.若,是方程的两个根,则( )
A. B. C. D.
9.商场将进价为50元/件的某种商品以80元/件出售时每天能卖出30件.经调查发现,每降价1元,每天可多卖出5件,若降价元,每天将盈利1080元,则可列方程为( )
A. B.
C. D.
10.如图,四边形是正方形, 点分别在的延长线上, 且,设. 给出下面三个结论:①;②;③上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
二、填空题(本题有6小题,每小题3分,共18分)
11.如果式子有意义,则的取值范围为 .
12.已知一组数据:6、a、3、4、8、7的众数为8,则这组数据的中位数是 .
13.如果一个多边形的每个外角都等于,则这个多边形的边数为 .
14.若是完全平方式,求常数的值 ;
15.如图,菱形的顶点与对角线交点都在反比例函数的图像上,对角线交轴于点,,且的面积为15,则 ;延长交轴于点,则点的坐标为 .
16.如图,在矩形中,,点,为直线上的两个动点,且,将线段关于翻折得线段,连接.当线段的长度最小时,的度数为 度.
三、解答题(本题有7小题,共52分,各小题都必须写出解答过程)
17.计算:.
18.解方程:
(1);
(2).
19.已知:如图,在 中,、的平分线分别交对角线于点、求证:四边形是平行四边形.
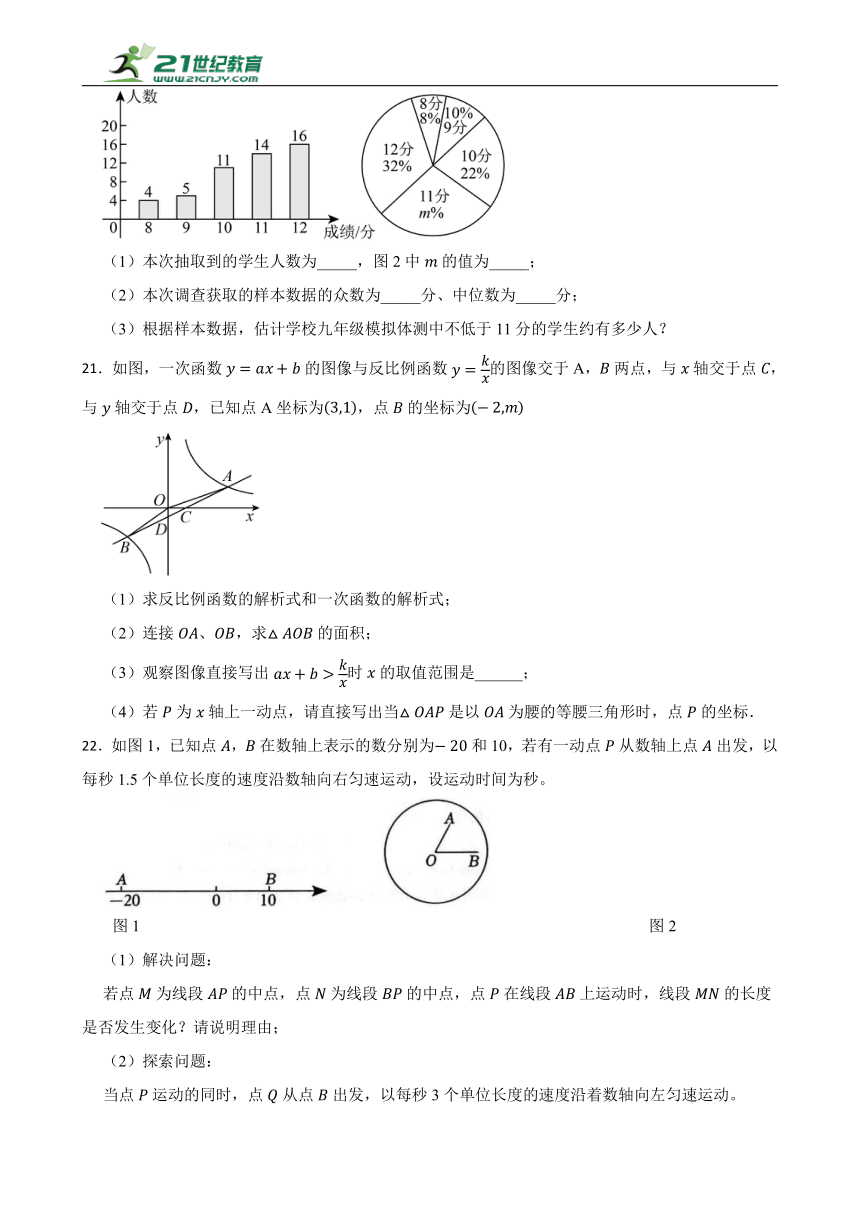
20.一初中九年级有2000名学生,在体育中考前进行一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
(1)本次抽取到的学生人数为_____,图2中的值为_____;
(2)本次调查获取的样本数据的众数为_____分、中位数为_____分;
(3)根据样本数据,估计学校九年级模拟体测中不低于11分的学生约有多少人?
21.如图,一次函数的图像与反比例函数的图像交于A,两点,与轴交于点,与轴交于点,已知点A坐标为,点的坐标为
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接、,求的面积;
(3)观察图像直接写出时的取值范围是______;
(4)若为轴上一动点,请直接写出当是以为腰的等腰三角形时,点的坐标.
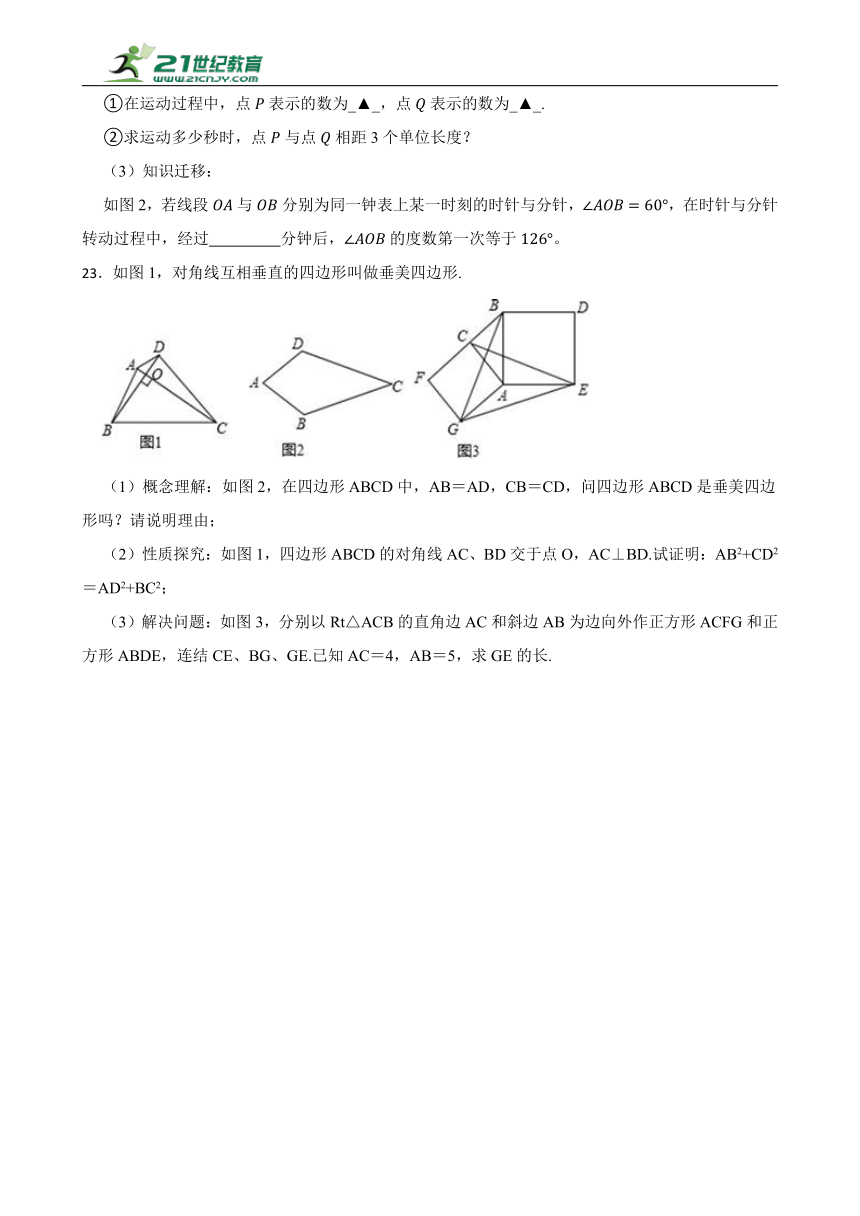
22.如图1,已知点,在数轴上表示的数分别为和10,若有一动点从数轴上点出发,以每秒1.5个单位长度的速度沿数轴向右匀速运动,设运动时间为秒。
图1 图2
(1)解决问题:
若点为线段的中点,点为线段的中点,点在线段上运动时,线段的长度是否发生变化?请说明理由;
(2)探索问题:
当点运动的同时,点从点出发,以每秒3个单位长度的速度沿着数轴向左匀速运动。
①在运动过程中,点表示的数为_▲_,点表示的数为_▲_.
②求运动多少秒时,点与点相距3个单位长度?
(3)知识迁移:
如图2,若线段与分别为同一钟表上某一时刻的时针与分针,,在时针与分针转动过程中,经过 分钟后,的度数第一次等于。
23.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
答案解析部分
1.A
2.C
3.B
解:A、,原选项计算错误,不符合题意;
B、,原选项计算正确,符合题意;
C、与不是同类二次根式,不能进行加减,原选项计算错误,不符合题意;
D、,原选项计算错误,不符合题意;
故选: B.
根据二次根式的运算法则逐项进行判断即可求出答案.
4.C
5.C
6.A
解:用反证法证明命题“在中,,求证:”,应先假设,
故答案为:A.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一 一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
7.B
解:∵5个均不相等的正数a1,a2,7,a3,a4的平均数为7,
∴
∴
∴正数a1,a2,a3,a4的平均数为7,
∴ 与原数据的平均数相同,
,,
∴,
故答案为:B.
根据平均数的定义得到则正数a1,a2,a3,a4的平均数为7,分别根据方差的计算法则计算出,即可求解.
8.D
9.D
解:设降价x元,则销售量为(30+5x)件,根据题意得:
(80-50-x)(30+5x)=1080
故答案为:D
本题考查一元二次方程的应用---销售问题,利用总利润=单利×销售数量。根据题意,得出单件商品的利润和销售数量是关键。进价为50元,售价为80-50-x,销售数量为30+5x,列出方程即可。
10.A
解:∵四边形ABCD是正方形,
∴,
∵,
∴,
∴,
∴,
∵,
∴,故①正确;
∵,即:,
∴,
∴,故②正确;
∵,且E、F为动点,
∴无法确定和的关系,故③错误,
综上,正确的有①②.
故答案为:A.
由正方形的性质得AD=AB=BC,∠DAB=∠ABC=90°,从而由SAS判断出△DAE≌△BAF,由全等三角形的对应边相等得AF=DE=c,结合三角形的三边关系判断①;根据勾股定理得a2+b2=c2,由偶数次幂的非负性得完(b-a)2>0,再展开后整体代入可判定②;勾股定理判断③.
11.
解:要使 有意义,则x-7≥0,∴ x≥7
故答案为:x≥7.
本题考查二次根式有意义的条件:被开方数大于等于0.满足这个条件即可。
12.
13.10
解:.
故这个多边形的边数为10.
故答案为:10.
由于任何多边形的外角和都等于360°,故用外角和的总度数除以每一个外角的度数即可求出多边形的边数.
14.或10
15.8;
16.75
17.
18.(1)解:,
,
∴,;
(2)解:,
,
或,
∴,.
()先把两边的公因数约去,再利用直接开平方法求解即可;
()当方程两边有公因式时,先移项再提公因式求解即可.
(1)解:
,
,
∴,;
(2)解:,
,
或,
∴,.
19.证明:四边形是平行四边形,
,,,
平分,平分,
,,
,,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
利用平行四边形的性质和角平分线的定义得到角度和边长的数量关系,根据这些数量关系证明和全等;利用全等的性质得到BM=DN,;再利用角度的数量关系证明BM∥DN ,从而根据平行四边形的判定,即可证明得到四边形是平行四边形.
20.(1)50,28
(2)12,11
(3)1200
21.(1);
(2)
(3)或
(4)或或
22.(1)解:如图,点在线段上运动时,线段的长度不发生变化,
理由如下:
点为线段的中点,点为线段的中点,
,,
点在线段上运动时,线段的长度不发生变化;
(2)解:①,;
②点与点相距3个单位长度,分两种情况:
如图,当点在点左侧时,,解得,
如图,当点在点右侧时,,解得,
综上所述,运动6或秒时,点与点相距3个单位长度;
(3)12
解:(2)①点,在数轴上表示的数分别为和10,则在运动过程中,点表示的数为,点表示的数为,
故答案为:,;
(3)时针每小时转=30°,分针每分转=6°,
设经过x分钟后,∠AOB 的度数第一次等于126°,
根据题意得:6x+60 0.5x=126,
解得:x=12,
∴经过12分钟后,∠AOB 的度数第一次等于126°.
故答案为:12.
(1)先利用线段中点的性质可得,,再利用线段的和差及等量代换可得,从而得解;
(2)①利用数轴上两点之间的距离公式求出点P、Q表示的数即可;
②分类讨论:第一种情况:当点在点左侧时;第二种情况:当点在点右侧时,再分别画出图形并列出方程求解即可;
(3)设经过x分钟后,∠AOB 的度数第一次等于126°,根据“∠AOB 的度数第一次等于126°”列出方程6x+60 0.5x=126,再求解即可.
23.(1)解:四边形ABCD是垂美四边形.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)解:如图2,
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2.
(3)解:连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4 ,BE=5 ,
∴GE2=CG2+BE2﹣CB2=73,
∴GE= .
(1)根据垂直平分线的判定定理证明即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.
2024-2025学年八年级下册期末模拟卷(义乌市专用)
数 学
(考试范围:八下全册 考试时间:100分钟 分值:100分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.下列属于一元二次方程的是( )
A. B. C. D.
3.下列各式计算正确的是( )
A. B. C. D.
4.如图,在矩形中,点A、B在y轴上,轴,对角线交于点E,,,反比例函数经过C、E两点,则k的值为( )
A.7 B.8 C.9 D.10
5.两张全等的矩形纸片,按如图所示的方式交叉叠放,,,与交于点G,与交于点H.若,,则四边形的面积为( )
A.4 B. C.8 D.16
6.用反证法证明命题“在中,,求证:”,应先假设( )
A. B. C. D.
7.已知5个均不相等的正数a1,a2,7,a3,a4的平均数为7,方差为,而a1,a2,a3,a4,这四个数的方差,则下列正确的是
A. B. C. D.
8.若,是方程的两个根,则( )
A. B. C. D.
9.商场将进价为50元/件的某种商品以80元/件出售时每天能卖出30件.经调查发现,每降价1元,每天可多卖出5件,若降价元,每天将盈利1080元,则可列方程为( )
A. B.
C. D.
10.如图,四边形是正方形, 点分别在的延长线上, 且,设. 给出下面三个结论:①;②;③上述结论中,所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
二、填空题(本题有6小题,每小题3分,共18分)
11.如果式子有意义,则的取值范围为 .
12.已知一组数据:6、a、3、4、8、7的众数为8,则这组数据的中位数是 .
13.如果一个多边形的每个外角都等于,则这个多边形的边数为 .
14.若是完全平方式,求常数的值 ;
15.如图,菱形的顶点与对角线交点都在反比例函数的图像上,对角线交轴于点,,且的面积为15,则 ;延长交轴于点,则点的坐标为 .
16.如图,在矩形中,,点,为直线上的两个动点,且,将线段关于翻折得线段,连接.当线段的长度最小时,的度数为 度.
三、解答题(本题有7小题,共52分,各小题都必须写出解答过程)
17.计算:.
18.解方程:
(1);
(2).
19.已知:如图,在 中,、的平分线分别交对角线于点、求证:四边形是平行四边形.
20.一初中九年级有2000名学生,在体育中考前进行一次模拟体测,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
(1)本次抽取到的学生人数为_____,图2中的值为_____;
(2)本次调查获取的样本数据的众数为_____分、中位数为_____分;
(3)根据样本数据,估计学校九年级模拟体测中不低于11分的学生约有多少人?
21.如图,一次函数的图像与反比例函数的图像交于A,两点,与轴交于点,与轴交于点,已知点A坐标为,点的坐标为
(1)求反比例函数的解析式和一次函数的解析式;
(2)连接、,求的面积;
(3)观察图像直接写出时的取值范围是______;
(4)若为轴上一动点,请直接写出当是以为腰的等腰三角形时,点的坐标.
22.如图1,已知点,在数轴上表示的数分别为和10,若有一动点从数轴上点出发,以每秒1.5个单位长度的速度沿数轴向右匀速运动,设运动时间为秒。
图1 图2
(1)解决问题:
若点为线段的中点,点为线段的中点,点在线段上运动时,线段的长度是否发生变化?请说明理由;
(2)探索问题:
当点运动的同时,点从点出发,以每秒3个单位长度的速度沿着数轴向左匀速运动。
①在运动过程中,点表示的数为_▲_,点表示的数为_▲_.
②求运动多少秒时,点与点相距3个单位长度?
(3)知识迁移:
如图2,若线段与分别为同一钟表上某一时刻的时针与分针,,在时针与分针转动过程中,经过 分钟后,的度数第一次等于。
23.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
答案解析部分
1.A
2.C
3.B
解:A、,原选项计算错误,不符合题意;
B、,原选项计算正确,符合题意;
C、与不是同类二次根式,不能进行加减,原选项计算错误,不符合题意;
D、,原选项计算错误,不符合题意;
故选: B.
根据二次根式的运算法则逐项进行判断即可求出答案.
4.C
5.C
6.A
解:用反证法证明命题“在中,,求证:”,应先假设,
故答案为:A.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一 一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
7.B
解:∵5个均不相等的正数a1,a2,7,a3,a4的平均数为7,
∴
∴
∴正数a1,a2,a3,a4的平均数为7,
∴ 与原数据的平均数相同,
,,
∴,
故答案为:B.
根据平均数的定义得到则正数a1,a2,a3,a4的平均数为7,分别根据方差的计算法则计算出,即可求解.
8.D
9.D
解:设降价x元,则销售量为(30+5x)件,根据题意得:
(80-50-x)(30+5x)=1080
故答案为:D
本题考查一元二次方程的应用---销售问题,利用总利润=单利×销售数量。根据题意,得出单件商品的利润和销售数量是关键。进价为50元,售价为80-50-x,销售数量为30+5x,列出方程即可。
10.A
解:∵四边形ABCD是正方形,
∴,
∵,
∴,
∴,
∴,
∵,
∴,故①正确;
∵,即:,
∴,
∴,故②正确;
∵,且E、F为动点,
∴无法确定和的关系,故③错误,
综上,正确的有①②.
故答案为:A.
由正方形的性质得AD=AB=BC,∠DAB=∠ABC=90°,从而由SAS判断出△DAE≌△BAF,由全等三角形的对应边相等得AF=DE=c,结合三角形的三边关系判断①;根据勾股定理得a2+b2=c2,由偶数次幂的非负性得完(b-a)2>0,再展开后整体代入可判定②;勾股定理判断③.
11.
解:要使 有意义,则x-7≥0,∴ x≥7
故答案为:x≥7.
本题考查二次根式有意义的条件:被开方数大于等于0.满足这个条件即可。
12.
13.10
解:.
故这个多边形的边数为10.
故答案为:10.
由于任何多边形的外角和都等于360°,故用外角和的总度数除以每一个外角的度数即可求出多边形的边数.
14.或10
15.8;
16.75
17.
18.(1)解:,
,
∴,;
(2)解:,
,
或,
∴,.
()先把两边的公因数约去,再利用直接开平方法求解即可;
()当方程两边有公因式时,先移项再提公因式求解即可.
(1)解:
,
,
∴,;
(2)解:,
,
或,
∴,.
19.证明:四边形是平行四边形,
,,,
平分,平分,
,,
,,
在和中,
,
≌,
,,
,,
,
,
四边形是平行四边形.
利用平行四边形的性质和角平分线的定义得到角度和边长的数量关系,根据这些数量关系证明和全等;利用全等的性质得到BM=DN,;再利用角度的数量关系证明BM∥DN ,从而根据平行四边形的判定,即可证明得到四边形是平行四边形.
20.(1)50,28
(2)12,11
(3)1200
21.(1);
(2)
(3)或
(4)或或
22.(1)解:如图,点在线段上运动时,线段的长度不发生变化,
理由如下:
点为线段的中点,点为线段的中点,
,,
点在线段上运动时,线段的长度不发生变化;
(2)解:①,;
②点与点相距3个单位长度,分两种情况:
如图,当点在点左侧时,,解得,
如图,当点在点右侧时,,解得,
综上所述,运动6或秒时,点与点相距3个单位长度;
(3)12
解:(2)①点,在数轴上表示的数分别为和10,则在运动过程中,点表示的数为,点表示的数为,
故答案为:,;
(3)时针每小时转=30°,分针每分转=6°,
设经过x分钟后,∠AOB 的度数第一次等于126°,
根据题意得:6x+60 0.5x=126,
解得:x=12,
∴经过12分钟后,∠AOB 的度数第一次等于126°.
故答案为:12.
(1)先利用线段中点的性质可得,,再利用线段的和差及等量代换可得,从而得解;
(2)①利用数轴上两点之间的距离公式求出点P、Q表示的数即可;
②分类讨论:第一种情况:当点在点左侧时;第二种情况:当点在点右侧时,再分别画出图形并列出方程求解即可;
(3)设经过x分钟后,∠AOB 的度数第一次等于126°,根据“∠AOB 的度数第一次等于126°”列出方程6x+60 0.5x=126,再求解即可.
23.(1)解:四边形ABCD是垂美四边形.
证明:∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)解:如图2,
∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2.
(3)解:连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4 ,BE=5 ,
∴GE2=CG2+BE2﹣CB2=73,
∴GE= .
(1)根据垂直平分线的判定定理证明即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.
同课章节目录
