河南省洛阳市新安县2025年九年级下学期第三次联考中考模拟数学试题(含部分答案)
文档属性
| 名称 | 河南省洛阳市新安县2025年九年级下学期第三次联考中考模拟数学试题(含部分答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 21:34:02 | ||
图片预览


文档简介
2024-2025学年九年级第三次质量检测试卷
数学
(满分120分,考试时间100分钟)
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1. 下表是某一时刻河南四个城市的气温情况,其中气温最低的城市是( )
郑州 开封 洛阳 濮阳
A. 郑州 B. 开封 C. 洛阳 D. 濮阳
2. 如图是月牙纹彩陶罐,是仰韶村遗址第三次发掘出土的唯一一件完整的彩陶罐,现藏于三门峡庙底沟博物馆.关于它的三视图,下列说法正确的是( )
A. 主视图和俯视图相同 B. 左视图和俯视图相同
C. 主视图和左视图相同 D. 三视图各不相同
3. 如图,在同一平面内,过直线l 上 一 点作,,则直线和直线重合的理由 ( )
A. 两点确定一条直线 B. 垂线段最短
C. 与线段两个端点距离相等的点在这条线段的垂直平分线上 D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
4. 我们规定关于任意正整数m,n的一种新运算:,如:.若,那么的结果是( )
A. B. C. D.
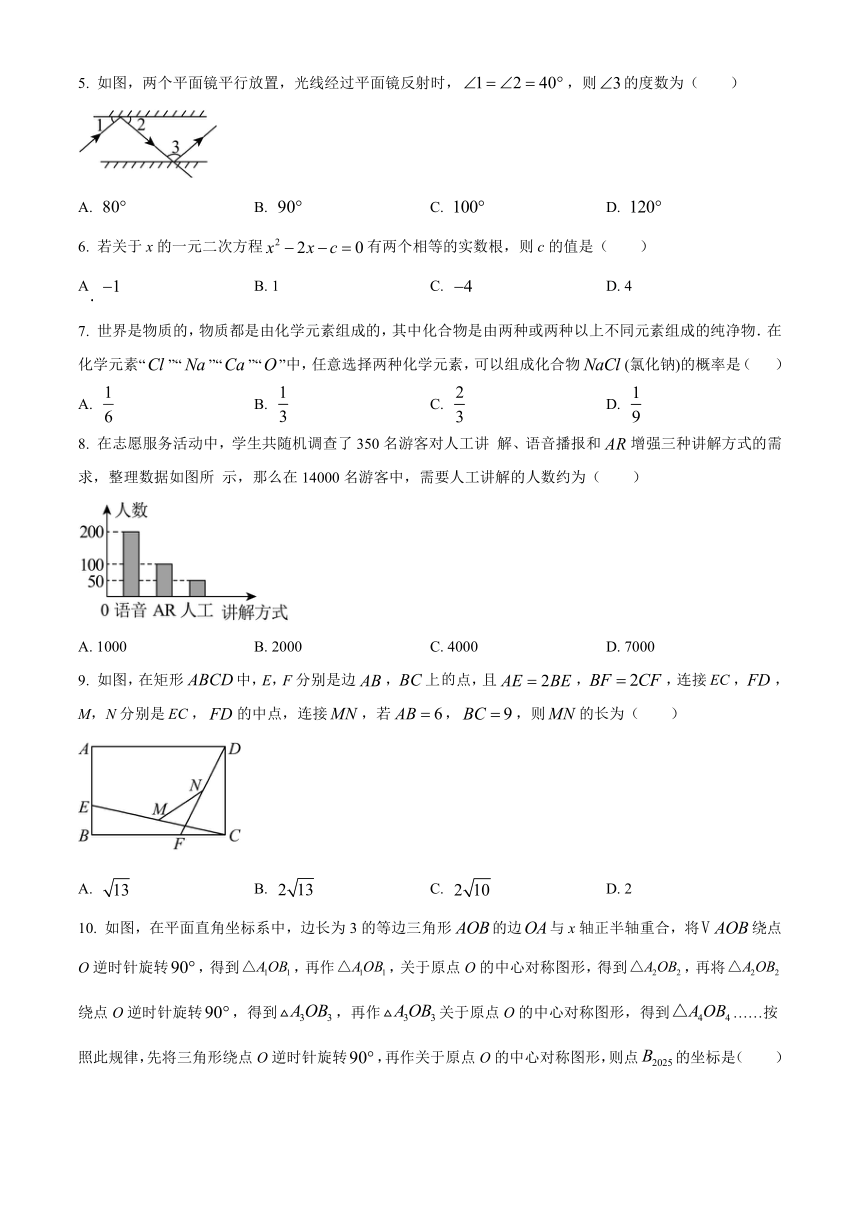
5. 如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
6. 若关于x的一元二次方程有两个相等的实数根,则c的值是( )
A B. 1 C. D. 4
7. 世界是物质的,物质都是由化学元素组成的,其中化合物是由两种或两种以上不同元素组成的纯净物.在化学元素“”“”“”“”中,任意选择两种化学元素,可以组成化合物(氯化钠)的概率是( )
A. B. C. D.
8. 在志愿服务活动中,学生共随机调查了350名游客对人工讲 解、语音播报和增强三种讲解方式的需求,整理数据如图所 示,那么在14000名游客中,需要人工讲解的人数约为( )
A. 1000 B. 2000 C. 4000 D. 7000
9. 如图,在矩形中,E,F分别是边,上点,且,,连接,,M,N分别是,的中点,连接,若,,则的长为( )
A. B. C. D. 2
10. 如图,在平面直角坐标系中,边长为3的等边三角形的边与x轴正半轴重合,将绕点O逆时针旋转,得到,再作,关于原点O的中心对称图形,得到,再将绕点O逆时针旋转,得到,再作关于原点O的中心对称图形,得到……按照此规律,先将三角形绕点O逆时针旋转,再作关于原点O的中心对称图形,则点的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共15分)
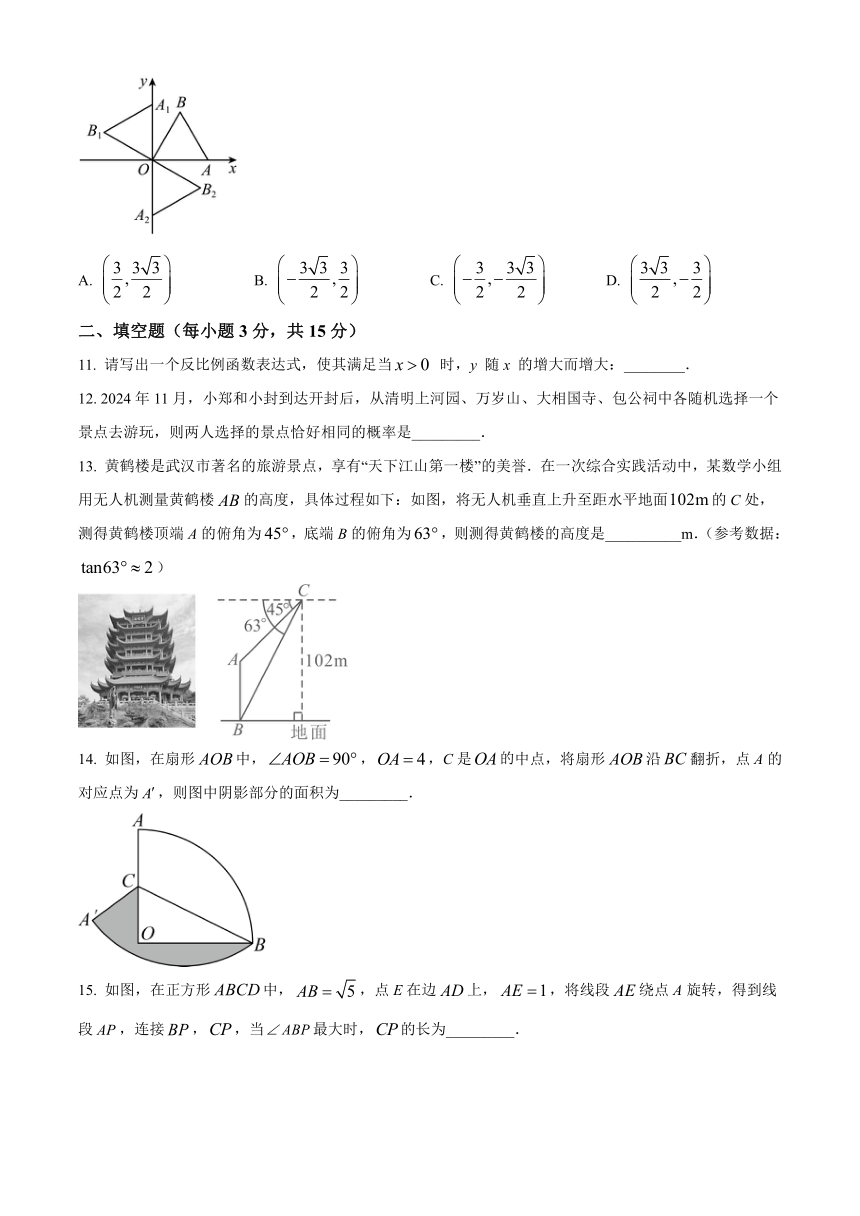
11. 请写出一个反比例函数表达式,使其满足当 时,y 随x 的增大而增大:________.
12. 2024年11月,小郑和小封到达开封后,从清明上河园、万岁山、大相国寺、包公祠中各随机选择一个景点去游玩,则两人选择的景点恰好相同的概率是_________.
13. 黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
14. 如图,在扇形中,,,C是中点,将扇形沿翻折,点A的对应点为,则图中阴影部分的面积为_________.
15. 如图,在正方形中,,点E在边上,,将线段绕点A旋转,得到线段,连接,,当最大时,的长为_________.
三、解答题(本大题共8个小题,共75分)
16. (1)计算:;
(2)化简:
17. 为了解七年级男生体能情况,某校随机抽取了七年级20名男生进行体能测试,并对测试成绩(单位:分)进行了统计分析:
【收集数据】
100 94 88 88 52 79 83 64 83 87
76 89 91 68 77 97 72 83 96 73
【整理数据】
该校规定:为不合格,为合格,为良好,为优秀.(成绩用表示)
等次 频数(人数) 频率
不合格 1 0.05
合格 a 0.20
良好 10 0.50
优秀 5 b
合计 20 100
【分析数据】
此组数据的平均数是82,众数是83,中位数是c;
【解决问题】
(1)填空:__________,__________,__________;
(2)若该校七年级共有300名男生,估计体能测试能达到优秀的男生约有多少人?
(3)根据上述统计分析情况,写一条你的看法.
18. 如图,已知点在直线上,双曲线经过点A.
(1)求双曲线的函数表达式.
(2)请分别画出直线和双曲线.
(3)点分别在直线和双曲线上,当时,直接写出b的取值范围.
19. 如图,在 中,,D 是 边的中点.
(1)用无刻度的直尺和圆规在边上作点E, 使(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 并延长至点F, 使,连接, 求证:.
20. 研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的扫描仪采集纪念碑的相关数据.
数据采集:如图,点是纪念碑顶部一点,的长表示点到水平地面的距离.航模从纪念碑前水平地面的点处竖直上升,飞行至距离地面20米的点处时,测得点的仰角;然后沿方向继续飞行,飞行方向与水平线的夹角,当到达点正上方的点处时,测得米;
数据应用:已知图中各点均在同一竖直平面内,,,三点在同一直线上.请根据上述数据,计算纪念碑顶部点到地面的距离的长(结果精确到1米.参考数据:,,,,,.
21. 学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:
甲型号大客车 乙型号大客车
满座载客量(人/辆) 55 35
租车费用(元/辆) 1200 800
(1)若租用的12辆大客车恰好能一次将八年级师生送到研学基地,求应分别租用甲、乙型号的大客车多少辆?
(2)设租用甲型号大客车x辆,租车总费用为y元.
①求出y(元)与x(辆)的函数关系式,并求出x的取值范围;
②当租用甲型号大客车多少辆时,租车的总费用最少,最少费用是多少?
22. 郑州彩虹桥以其独特的造型成为城市地标,三个连续拱形设计雄伟壮观.已知彩虹桥中间拱形的最高点距离桥面,建立如图所示的平面直角坐标系,中间拱形的一端点为坐标原点,另一端点为,拱的形状可以近似看作二次函数图像的一部分.
(1)求彩虹桥中间拱形的二次函数表达式.
(2)一架无人机从原点出发,沿着拱形的轨迹匀速飞行,已知无人机飞行时在水平方向的速度为,同时有一遥控车从原点出发,沿方向以的速度匀速行驶,设运动时间为,问在运动过程中,是否存在某一时刻t,使得无人机到点O的距离是遥控车到点距离的倍?若存在,求出的值;若不存在,请说明理由.
23 综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.数学活动课上,老师准备了若干张正方形纸片, 组织同学们进行折纸探究活动.
【动手操作】如图1,将正方形纸片对折,使与重合,展开纸片,得到折痕;过 点M,C 折叠纸片,使点B 落在点处;再沿过点C的直线折叠纸片使得与重合,折痕交于点E.求知小组的同学们通过观察猜测E是的三等分点,并进行证明,过程如下:
设,则 ,.
∵四边形是正方形,∴.
由折叠的性质,得,,
∴,即三点在同一条直线上
在中,,可列方程① , 整理,得 ②
∴,即E是的三等分点.
(1)请将上述过程补充完整:① ;② .
【深入探究】乐学小组尝试了另一种折叠方法,如图2,将正方形纸片对折,使与重合,展开纸片,得到折痕;折叠纸片,使点C与点M重合,折痕交于点E,交于点F,点D的对应点为,交于点G.
(2)判断点G 是否为的三等分点,并说明理由.
【拓展延伸】善思小组继续探究,如图3,将正方形纸片沿过点C的直线折叠,使点B落在点处,折痕交边于点E;再沿过点C的直线折叠,使与重合,折痕交边于点F,将沿折叠,得到.
(3)若正方形的边长为6,当点P 落在的边上时,请直接写出的长.
2024-2025学年九年级第三次质量检测试卷
数学
(满分120分,考试时间100分钟)
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】D
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】A
【8题答案】
【答案】B
【9题答案】
【答案】A
【10题答案】
【答案】B
二、填空题(每小题3分,共15分)
【11题答案】
【答案】
【12题答案】
【答案】
【13题答案】
【答案】51
【14题答案】
【答案】##
【15题答案】
【答案】或
三、解答题(本大题共8个小题,共75分)
【16题答案】
【答案】();().
【17题答案】
【答案】(1)4,0.25,83
(2)75人 (3)男生体能状况良好
【18题答案】
【答案】(1)
(2)见解析 (3)或
【19题答案】
【答案】(1)见解析 (2)见解析
【20题答案】
【答案】点A到地面的距离的长约为27米
【21题答案】
【答案】(1)租用甲型号的大客车8辆,租用甲型号的大客车4辆;
(2)①;②租用甲型号的大客车8辆,租用甲型号的大客车4辆时,费用最少,为12800元
【22题答案】
【答案】(1)
(2)存在,
【23题答案】
【答案】(1)① ② (2)是;理由见解析 (3)或
数学
(满分120分,考试时间100分钟)
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
1. 下表是某一时刻河南四个城市的气温情况,其中气温最低的城市是( )
郑州 开封 洛阳 濮阳
A. 郑州 B. 开封 C. 洛阳 D. 濮阳
2. 如图是月牙纹彩陶罐,是仰韶村遗址第三次发掘出土的唯一一件完整的彩陶罐,现藏于三门峡庙底沟博物馆.关于它的三视图,下列说法正确的是( )
A. 主视图和俯视图相同 B. 左视图和俯视图相同
C. 主视图和左视图相同 D. 三视图各不相同
3. 如图,在同一平面内,过直线l 上 一 点作,,则直线和直线重合的理由 ( )
A. 两点确定一条直线 B. 垂线段最短
C. 与线段两个端点距离相等的点在这条线段的垂直平分线上 D. 在同一平面内,过一点有且只有一条直线与已知直线垂直
4. 我们规定关于任意正整数m,n的一种新运算:,如:.若,那么的结果是( )
A. B. C. D.
5. 如图,两个平面镜平行放置,光线经过平面镜反射时,,则的度数为( )
A. B. C. D.
6. 若关于x的一元二次方程有两个相等的实数根,则c的值是( )
A B. 1 C. D. 4
7. 世界是物质的,物质都是由化学元素组成的,其中化合物是由两种或两种以上不同元素组成的纯净物.在化学元素“”“”“”“”中,任意选择两种化学元素,可以组成化合物(氯化钠)的概率是( )
A. B. C. D.
8. 在志愿服务活动中,学生共随机调查了350名游客对人工讲 解、语音播报和增强三种讲解方式的需求,整理数据如图所 示,那么在14000名游客中,需要人工讲解的人数约为( )
A. 1000 B. 2000 C. 4000 D. 7000
9. 如图,在矩形中,E,F分别是边,上点,且,,连接,,M,N分别是,的中点,连接,若,,则的长为( )
A. B. C. D. 2
10. 如图,在平面直角坐标系中,边长为3的等边三角形的边与x轴正半轴重合,将绕点O逆时针旋转,得到,再作,关于原点O的中心对称图形,得到,再将绕点O逆时针旋转,得到,再作关于原点O的中心对称图形,得到……按照此规律,先将三角形绕点O逆时针旋转,再作关于原点O的中心对称图形,则点的坐标是( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11. 请写出一个反比例函数表达式,使其满足当 时,y 随x 的增大而增大:________.
12. 2024年11月,小郑和小封到达开封后,从清明上河园、万岁山、大相国寺、包公祠中各随机选择一个景点去游玩,则两人选择的景点恰好相同的概率是_________.
13. 黄鹤楼是武汉市著名的旅游景点,享有“天下江山第一楼”的美誉.在一次综合实践活动中,某数学小组用无人机测量黄鹤楼的高度,具体过程如下:如图,将无人机垂直上升至距水平地面的C处,测得黄鹤楼顶端A的俯角为,底端B的俯角为,则测得黄鹤楼的高度是__________m.(参考数据:)
14. 如图,在扇形中,,,C是中点,将扇形沿翻折,点A的对应点为,则图中阴影部分的面积为_________.
15. 如图,在正方形中,,点E在边上,,将线段绕点A旋转,得到线段,连接,,当最大时,的长为_________.
三、解答题(本大题共8个小题,共75分)
16. (1)计算:;
(2)化简:
17. 为了解七年级男生体能情况,某校随机抽取了七年级20名男生进行体能测试,并对测试成绩(单位:分)进行了统计分析:
【收集数据】
100 94 88 88 52 79 83 64 83 87
76 89 91 68 77 97 72 83 96 73
【整理数据】
该校规定:为不合格,为合格,为良好,为优秀.(成绩用表示)
等次 频数(人数) 频率
不合格 1 0.05
合格 a 0.20
良好 10 0.50
优秀 5 b
合计 20 100
【分析数据】
此组数据的平均数是82,众数是83,中位数是c;
【解决问题】
(1)填空:__________,__________,__________;
(2)若该校七年级共有300名男生,估计体能测试能达到优秀的男生约有多少人?
(3)根据上述统计分析情况,写一条你的看法.
18. 如图,已知点在直线上,双曲线经过点A.
(1)求双曲线的函数表达式.
(2)请分别画出直线和双曲线.
(3)点分别在直线和双曲线上,当时,直接写出b的取值范围.
19. 如图,在 中,,D 是 边的中点.
(1)用无刻度的直尺和圆规在边上作点E, 使(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 并延长至点F, 使,连接, 求证:.
20. 研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的扫描仪采集纪念碑的相关数据.
数据采集:如图,点是纪念碑顶部一点,的长表示点到水平地面的距离.航模从纪念碑前水平地面的点处竖直上升,飞行至距离地面20米的点处时,测得点的仰角;然后沿方向继续飞行,飞行方向与水平线的夹角,当到达点正上方的点处时,测得米;
数据应用:已知图中各点均在同一竖直平面内,,,三点在同一直线上.请根据上述数据,计算纪念碑顶部点到地面的距离的长(结果精确到1米.参考数据:,,,,,.
21. 学校决定按年级开展师生研学活动,该校八年级师生共580人将参加研学活动,计划租用12辆大客车,现有甲、乙两种型号的大客车,它们的满座载客量和租车费用如下表:
甲型号大客车 乙型号大客车
满座载客量(人/辆) 55 35
租车费用(元/辆) 1200 800
(1)若租用的12辆大客车恰好能一次将八年级师生送到研学基地,求应分别租用甲、乙型号的大客车多少辆?
(2)设租用甲型号大客车x辆,租车总费用为y元.
①求出y(元)与x(辆)的函数关系式,并求出x的取值范围;
②当租用甲型号大客车多少辆时,租车的总费用最少,最少费用是多少?
22. 郑州彩虹桥以其独特的造型成为城市地标,三个连续拱形设计雄伟壮观.已知彩虹桥中间拱形的最高点距离桥面,建立如图所示的平面直角坐标系,中间拱形的一端点为坐标原点,另一端点为,拱的形状可以近似看作二次函数图像的一部分.
(1)求彩虹桥中间拱形的二次函数表达式.
(2)一架无人机从原点出发,沿着拱形的轨迹匀速飞行,已知无人机飞行时在水平方向的速度为,同时有一遥控车从原点出发,沿方向以的速度匀速行驶,设运动时间为,问在运动过程中,是否存在某一时刻t,使得无人机到点O的距离是遥控车到点距离的倍?若存在,求出的值;若不存在,请说明理由.
23 综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.数学活动课上,老师准备了若干张正方形纸片, 组织同学们进行折纸探究活动.
【动手操作】如图1,将正方形纸片对折,使与重合,展开纸片,得到折痕;过 点M,C 折叠纸片,使点B 落在点处;再沿过点C的直线折叠纸片使得与重合,折痕交于点E.求知小组的同学们通过观察猜测E是的三等分点,并进行证明,过程如下:
设,则 ,.
∵四边形是正方形,∴.
由折叠的性质,得,,
∴,即三点在同一条直线上
在中,,可列方程① , 整理,得 ②
∴,即E是的三等分点.
(1)请将上述过程补充完整:① ;② .
【深入探究】乐学小组尝试了另一种折叠方法,如图2,将正方形纸片对折,使与重合,展开纸片,得到折痕;折叠纸片,使点C与点M重合,折痕交于点E,交于点F,点D的对应点为,交于点G.
(2)判断点G 是否为的三等分点,并说明理由.
【拓展延伸】善思小组继续探究,如图3,将正方形纸片沿过点C的直线折叠,使点B落在点处,折痕交边于点E;再沿过点C的直线折叠,使与重合,折痕交边于点F,将沿折叠,得到.
(3)若正方形的边长为6,当点P 落在的边上时,请直接写出的长.
2024-2025学年九年级第三次质量检测试卷
数学
(满分120分,考试时间100分钟)
一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的)
【1题答案】
【答案】D
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】D
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】A
【8题答案】
【答案】B
【9题答案】
【答案】A
【10题答案】
【答案】B
二、填空题(每小题3分,共15分)
【11题答案】
【答案】
【12题答案】
【答案】
【13题答案】
【答案】51
【14题答案】
【答案】##
【15题答案】
【答案】或
三、解答题(本大题共8个小题,共75分)
【16题答案】
【答案】();().
【17题答案】
【答案】(1)4,0.25,83
(2)75人 (3)男生体能状况良好
【18题答案】
【答案】(1)
(2)见解析 (3)或
【19题答案】
【答案】(1)见解析 (2)见解析
【20题答案】
【答案】点A到地面的距离的长约为27米
【21题答案】
【答案】(1)租用甲型号的大客车8辆,租用甲型号的大客车4辆;
(2)①;②租用甲型号的大客车8辆,租用甲型号的大客车4辆时,费用最少,为12800元
【22题答案】
【答案】(1)
(2)存在,
【23题答案】
【答案】(1)① ② (2)是;理由见解析 (3)或
同课章节目录
