2025年高考数学考前押题卷(一)全国甲卷(含解析)
文档属性
| 名称 | 2025年高考数学考前押题卷(一)全国甲卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 637.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:40:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年高考数学考前押题卷(一)全国甲卷
注意事项:
1.本试卷满分150分,考试时间120分钟。
2.答题前,考生务必将姓名、考生号等个人信息填写在答题卡指定位置。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答。超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2025 亳州校级二模)若A={x|﹣2<x<2},,则A∩B=( )
A.{x|﹣1≤x≤2} B.{x|﹣1<x<2} C.{x|﹣2<x≤2} D.{x|﹣2≤x≤2}
2.(2025 开封模拟)已知向量,,若,则( )
A. B. C.5 D.20
3.(2025 河南校级模拟)已知的展开式中所有项的系数之和为3,则展开式中的常数项为( )
A.﹣60 B.100 C.﹣260 D.380
4.(2025 鞍山模拟)计算:( )
A. B. C. D.1
5.(2025 滨海新区三模)已知a=30.9,b=log29,c=e﹣ln3,则( )
A.b>a>c B.b>c>a C.c>a>b D.a>c>b
6.(2025 青州市校级模拟)若函数在区间(m,m+1)上不单调,则实数m的取值范围为( )
A. B. C. D.
7.(2025 江苏校级模拟)空间直角坐标系里有一点P(2,3,6),过P作一动平面m,直线l的方向向量坐标为(3,0,﹣1).当原点到m距离d最大时,下列说法正确的是( )
A.l⊥m B.l∥m C. D.d=7
8.(2025 哈尔滨校级模拟)过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
A.10 B.8 C.6 D.4
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
(多选)9.(2025 吉林四模)两批同种规格的产品,第一批占40%,次品率为3%;第二批占60%,次品率为2%,则( )
A.从两批产品中各取1件,都取到次品的概率为0.06%
B.从两批产品中各取1件,都取到次品的概率为2.4%
C.两批产品混合后任取1件,该产品是次品的概率为2.4%
D.两批产品混合后任取1件,若取到的是次品,则它取自第一批产品的概率为0.3%
(多选)10.(2025 金昌校级模拟)在△ABC中,,AB=2,BC=m,则“△ABC有唯一解”的充分条件可以是( )
A.m=1 B. C.m=2 D.
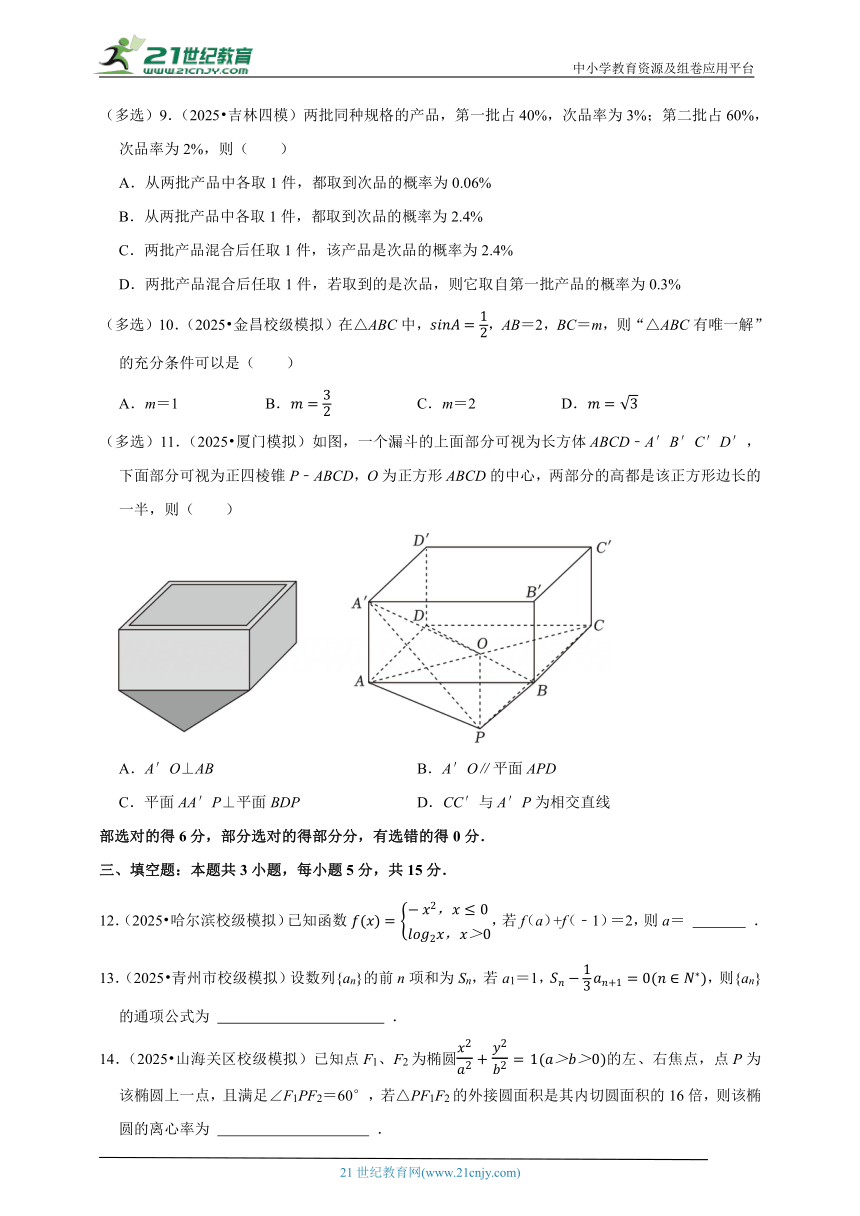
(多选)11.(2025 厦门模拟)如图,一个漏斗的上面部分可视为长方体ABCD﹣A′B′C′D′,下面部分可视为正四棱锥P﹣ABCD,O为正方形ABCD的中心,两部分的高都是该正方形边长的一半,则( )
A.A′O⊥AB B.A′O∥平面APD
C.平面AA′P⊥平面BDP D.CC′与A′P为相交直线
部选对的得6分,部分选对的得部分分,有选错的得0分.
三、填空题:本题共3小题,每小题5分,共15分.
12.(2025 哈尔滨校级模拟)已知函数,若f(a)+f(﹣1)=2,则a= .
13.(2025 青州市校级模拟)设数列{an}的前n项和为Sn,若a1=1,,则{an}的通项公式为 .
14.(2025 山海关区校级模拟)已知点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,且满足∠F1PF2=60°,若△PF1F2的外接圆面积是其内切圆面积的16倍,则该椭圆的离心率为 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(2025 江西模拟)已知△ABC是锐角三角形,角A,B,C的对边分别是a,b,c,c=2,且.
(1)求角B;
(2)求边a的取值范围.
16.(2025 南通模拟)已知数列{an}的前n项和为Sn,是首项和公差均为1的等差数列.
(1)求数列{an}的通项公式;
(2)若,求bn的最小值.
17.(2025 鞍山模拟)某校有高一学生1800人,高二学生1200人,学校采取按比例分配的分层抽样的方式从中抽取100人进行体育测试.测试后,统计得到高一样本的一分钟跳绳次数的均值为165,方差为61,高二样本的一分钟跳绳次数的均值为145,方差为31.
(1)计算总样本的一分钟跳绳次数的均值和方差;
(2)将一分钟跳绳次数≥125视为及格,整理出以下列联表:
及格 不及格 合计
高一 52 8 60
高二 38 2 40
合计 90 10 100
试根据小概率值α=0.05的独立性检验,分析一分钟跳绳次数及格情况是否与年级有关;(结果保留小数点后三位)
(3)如果将(2)表格中的所有数据都扩大为原来的10倍,在相同的检验标准下,再用独立性检验推断一分钟跳绳次数及格情况与年级之间的关联性,结果还一样吗?请你试着解释其中的原因.
附:,n=a+b+c+d.
χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18.(2025 金昌校级模拟)如图,在四棱锥P﹣ABCD中,PA⊥平面ABD,PA=AB=4,C,D是平面ABCD内以AB为直径的半圆上的两点,且AD=2,DC∥AB.
(1)证明:BD⊥平面PAD;
(2)证明:平面PAD⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值.
19.(2025 金昌校级模拟)在以O为坐标原点的平面直角坐标系中,F(2,0)为椭圆的右焦点,过点F的直线l(斜率存在)与Z交于A,B两点,线段AB的中点为M(不与O重合),直线OM与l的斜率之积为.
(1)证明:a2=2b2;
(2)设直线OM与直线x=4交于点N,若△AFN为等腰三角形,求l的一般式方程.
2025年高考数学考前押题卷(一)全国甲卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B B C B A C D B
二.多选题(共3小题)
题号 9 10 11
答案 AC AC BCD
一.选择题(共8小题)
1.(2025 亳州校级二模)若A={x|﹣2<x<2},,则A∩B=( )
A.{x|﹣1≤x≤2} B.{x|﹣1<x<2} C.{x|﹣2<x≤2} D.{x|﹣2≤x≤2}
【解答】解:A={x|﹣2<x<2},B={x|﹣1<x≤2},
∴A∩B={x|﹣1<x<2}.
故选:B.
2.(2025 开封模拟)已知向量,,若,则( )
A. B. C.5 D.20
【解答】解:已知,,
由,得1×x﹣2×2=0,即x=4,则,
可得.
故选:B.
3.(2025 河南校级模拟)已知的展开式中所有项的系数之和为3,则展开式中的常数项为( )
A.﹣60 B.100 C.﹣260 D.380
【解答】解:的展开式中所有项的系数之和为3,
令x=1,则(1+a)×(2﹣1)6=3,故a=2,
的展开式的通项公式为:,
故的展开式中的常数项为:
.
故选:C.
4.(2025 鞍山模拟)计算:( )
A. B. C. D.1
【解答】解:原式
.
故选:B.
5.(2025 滨海新区三模)已知a=30.9,b=log29,c=e﹣ln3,则( )
A.b>a>c B.b>c>a C.c>a>b D.a>c>b
【解答】解:由题意1,1<a=30.9<31=3,b=log29>log28=3,
所以b>a>c.
故选:A.
6.(2025 青州市校级模拟)若函数在区间(m,m+1)上不单调,则实数m的取值范围为( )
A. B. C. D.
【解答】解:根据题目:函数在区间(m,m+1)上不单调,
,令,
因为函数在区间(m,m+1)上不单调,
所以y=x2﹣3在(m,m+1)上有变号零点,
即,解得.
故选:C.
7.(2025 江苏校级模拟)空间直角坐标系里有一点P(2,3,6),过P作一动平面m,直线l的方向向量坐标为(3,0,﹣1).当原点到m距离d最大时,下列说法正确的是( )
A.l⊥m B.l∥m C. D.d=7
【解答】解:由题意,原点O到m距离d最大,即OP⊥m,点P(2,3,6),
此时,故C错误,D正确.
显然是平面m的一个法向量,而直线l的方向向量,
则,
但无法确定直线l与平面m的位置关系,所以l∥m或l m,故AB错误.
故选:D.
8.(2025 哈尔滨校级模拟)过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
A.10 B.8 C.6 D.4
【解答】解:由题设知知线段AB的中点到准线的距离为4,
设A,B两点到准线的距离分别为d1,d2,
由抛物线的定义知:
|AB|=|AF|+|BF|=d1+d2=2×4=8.
故选:B.
二.多选题(共3小题)
(多选)9.(2025 吉林四模)两批同种规格的产品,第一批占40%,次品率为3%;第二批占60%,次品率为2%,则( )
A.从两批产品中各取1件,都取到次品的概率为0.06%
B.从两批产品中各取1件,都取到次品的概率为2.4%
C.两批产品混合后任取1件,该产品是次品的概率为2.4%
D.两批产品混合后任取1件,若取到的是次品,则它取自第一批产品的概率为0.3%
【解答】解:依题意,从两批产品中各取1件,都取到次品的概率为3%×2%=0.06%,故A正确,B错误;
设事件A=“从混合后的产品中取出一件是次品”,B=“次品来自第一批产品”,C=“次品来自第二批产品”,
则P(B)=40%,P(C)=60%,P(A|B)=3%,P(A|C)=2%,
所以P(A)=P(B)P(A|B)+P(C)P(A|C=40%×3%+60%×2%=2.4%,故C正确;
因为,故D错误.
故选:AC.
(多选)10.(2025 金昌校级模拟)在△ABC中,,AB=2,BC=m,则“△ABC有唯一解”的充分条件可以是( )
A.m=1 B. C.m=2 D.
【解答】解:由正弦定理,即,可得.
当m=1时,sinC=1,结合C∈(0,π),可得,△ABC唯一存在,
所以由m=1可以推出△ABC有唯一解,故A正确;
当时,,结合AB>BC,可知,
满足条件的角C有互补的两个值,相应的△ABC有两解,故B错误;
当m=2时,可得AB=BC=2,所以,则,△ABC唯一存在,
所以由m=2可以推出△ABC有唯一解,故C正确;
当时,,结合AB>BC,可得,
满足条件的角C有互补的两个值,可知△ABC有两解,D项错误.
故选:AC.
(多选)11.(2025 厦门模拟)如图,一个漏斗的上面部分可视为长方体ABCD﹣A′B′C′D′,下面部分可视为正四棱锥P﹣ABCD,O为正方形ABCD的中心,两部分的高都是该正方形边长的一半,则( )
A.A′O⊥AB B.A′O∥平面APD
C.平面AA′P⊥平面BDP D.CC′与A′P为相交直线
【解答】解:对于A,设正方形ABCD边长为2,由正四棱锥性质可得PO⊥平面ABCD,故PO=AA′=1,
因为A′A⊥面ABCD,故A′O在底面的射影为AO,
又AO不与AB垂直,故A′O不与AB垂直,故A不正确;
对于B,由题PO∥AA′且PO=AA′,故四边形POA′A是平行四边形,
所以A′O∥AP,A′O不在平面APD内,AP 平面APD,
所以A′O∥平面APD,故B正确;
对于C,因为PO∥CC′∥AA′,O∈平面CC′AA′,故PO 平面CC′A′A,
平面AA′P即为平面CC′A′A,因为A′A⊥面ABCD,BD 面ABCD,
所以A′A⊥BD,又因为BD⊥AC,A′A∩AC=A,
所以BD⊥平面CC′A′A,又BD 平面BDP,
所以平面BDP⊥平面CC′A′A,即平面AA′P⊥平面BDP,故C正确;
对于D,由C可知CC′与A′P都在平面CC′A′A中且不平行,故CC与′A′P为相交直线,故D正确.
故选:BCD.
三.填空题(共3小题)
12.(2025 哈尔滨校级模拟)已知函数,若f(a)+f(﹣1)=2,则a= 8 .
【解答】解:因为函数,f(a)+f(﹣1)=2,
所以f(﹣1)=﹣1,
故f(a)=3,即log2a=3,解得a=8.
故答案为:8.
13.(2025 青州市校级模拟)设数列{an}的前n项和为Sn,若a1=1,,则{an}的通项公式为 .
【解答】解:∵,
∴,n≥2,
两式相减得:,n≥2,
∴an+1=4an,n≥2,
又,S1=a1,∴a2=3a1=3,
∴数列{an}除去首项1后,是一个以a2=3为首项,公比为4的等比数列,
,n≥2,
∴,
故答案为:.
14.(2025 山海关区校级模拟)已知点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,且满足∠F1PF2=60°,若△PF1F2的外接圆面积是其内切圆面积的16倍,则该椭圆的离心率为 .
【解答】解:如图,点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,可知|PF1|+|PF2|=2a,且|F1F2|=2c,又∠F1PF2=60°,
利用余弦定理可知:
,
化简可得,
∴△PF1F2的面积为,
设△PF1F2的外接圆半径为R,内切圆半径为r,
由正弦定理可得,可得,
易知△PF1F2的周长为l=|PF1|+|PF2|+|F1F2|=2a+2c,
利用等面积法可知,解得,
又△PF1F2的外接圆面积是其内切圆面积的16倍,即,∴,
即可得,
∴6c=4a,离心率.
故答案为:.
四.解答题(共5小题)
15.(2025 江西模拟)已知△ABC是锐角三角形,角A,B,C的对边分别是a,b,c,c=2,且.
(1)求角B;
(2)求边a的取值范围.
【解答】解:(1)因为,c=2,
所以,
故(a﹣c)sinC=csin(A﹣B),由正弦定理可得(sinA﹣sinC)sinC=sinC×sin(A﹣B),
又sinC≠0,故得到sinA﹣sinC=sin(A﹣B),
在三角形中,sin(A+B)=sinC,
即sinA﹣sin(A+B)=sin(A﹣B),即sinA﹣sinAcosB﹣cosAsinB=sinAcosB﹣sinBcosA
整理得sinA=2sinAcosB,因为sinA≠0,故,
又B是三角形的内角,所以0<B<π,
解得;
(2)已知△ABC是锐角三角形,
所以即则①
根据余弦定理得,即,
解得b2=a2﹣2a+4,②
将②代入①中,整理得又a>0,解得1<a<4,
即a∈(1,4)
法(ii)因为△ABC是锐角三角形,c=2,
由正弦定理可得,
可得a 21,
因为,可得A,
所以tanA,可得∈(0,3),
所以a∈(1,4).
16.(2025 南通模拟)已知数列{an}的前n项和为Sn,是首项和公差均为1的等差数列.
(1)求数列{an}的通项公式;
(2)若,求bn的最小值.
【解答】解:(1)由是首项和公差均为1的等差数列,
可得1+n﹣1=n,
即有Sn=n2,
当n=1时,a1=S1=1,
当n≥2时,an=Sn﹣Sn﹣1=n2﹣(n﹣1)2=2n﹣1,
上式符合首项,
则an=2n﹣1,n∈N*;
(2)若2n﹣10n+5,
则bn+1﹣bn=2n+1﹣10(n+1)+5﹣2n+10n﹣5=2n﹣10,
当1≤n≤3时,可得b1>b2>b3>b4,
当n≥4时,bn+1﹣bn>0,即有b4<b5<b6<...<bn,
则bn的最小值为b4=16﹣35=﹣19.
17.(2025 鞍山模拟)某校有高一学生1800人,高二学生1200人,学校采取按比例分配的分层抽样的方式从中抽取100人进行体育测试.测试后,统计得到高一样本的一分钟跳绳次数的均值为165,方差为61,高二样本的一分钟跳绳次数的均值为145,方差为31.
(1)计算总样本的一分钟跳绳次数的均值和方差;
(2)将一分钟跳绳次数≥125视为及格,整理出以下列联表:
及格 不及格 合计
高一 52 8 60
高二 38 2 40
合计 90 10 100
试根据小概率值α=0.05的独立性检验,分析一分钟跳绳次数及格情况是否与年级有关;(结果保留小数点后三位)
(3)如果将(2)表格中的所有数据都扩大为原来的10倍,在相同的检验标准下,再用独立性检验推断一分钟跳绳次数及格情况与年级之间的关联性,结果还一样吗?请你试着解释其中的原因.
附:,n=a+b+c+d.
χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
【解答】解:(1)由题意可知,高一样本量为100=60,高二样本量为100=40,
所以总样本均值为,
总样本方差为;
(2)零假设为H0:一分钟跳绳次数及格情况与年级无关,
根据列联表,,
所以根据小概率值α=0.05的独立性检验,推断H0成立,即一分钟跳绳次数及格情况与年级无关;
(3)将(2)表格中的所有数据都扩大为原来的10倍,
则,
所以根据小概率值α=0.05的独立性检验,推断H0不成立,即一分钟跳绳次数及格情况与年级有关,
所以将(2)表格中的所有数据都扩大为原来的10倍,结果不一样,
因为样本量增大使得相对差异的绝对值增大,导致卡方统计量显著上升.
18.(2025 金昌校级模拟)如图,在四棱锥P﹣ABCD中,PA⊥平面ABD,PA=AB=4,C,D是平面ABCD内以AB为直径的半圆上的两点,且AD=2,DC∥AB.
(1)证明:BD⊥平面PAD;
(2)证明:平面PAD⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值.
【解答】(1)证明:因为PA⊥平面ABD,BD 平面ABD,
所以PA⊥BD.
因为D是以AB为直径的半圆上的一点,
所以AD⊥BD,
因为PA,AD 平面PAD,PA∩AD=A,
所以BD⊥平面PAD.
(2)证明:因为BD 平面PBD,由(1)得BD⊥平面PAD,
所以平面PAD⊥平面PBD.
(3)解:以A为坐标原点,垂直于平面PAB的方向为x轴,的方向分别为y轴、z轴的正方向,
建立如图所示的空间直角坐标系A﹣xyz,
则,,
故.
设平面PBD的法向量为,
则,即,
令y=1,得,
可得 3+3﹣4=2,||2,||,
所以cos,.
设直线PC与平面PBD所成的角为θ,
所以sinθ=|cos,|.
19.(2025 金昌校级模拟)在以O为坐标原点的平面直角坐标系中,F(2,0)为椭圆的右焦点,过点F的直线l(斜率存在)与Z交于A,B两点,线段AB的中点为M(不与O重合),直线OM与l的斜率之积为.
(1)证明:a2=2b2;
(2)设直线OM与直线x=4交于点N,若△AFN为等腰三角形,求l的一般式方程.
【解答】解:(1)证明:设A(x1,y1),B(x2,y2),
因为A,B两点均在椭圆Z上,
所以,
两式相减得,
即,
设M(x0,y0),
此时x1+x2=2x0,y1+y2=2y0,
所以,
即,
则直线l的斜率,直线OM的斜率为,
所以直线OM与直线l的斜率之积为,
即,
则a2=2b2;
(2)因为椭圆的右焦点F(2,0),
所以c=2,
此时a2﹣b2=c2=4,
又a2=2b2,
解得a=2,b=2,
所以椭圆Z的方程为,
由(1)知,直线OM的方程为,
令x=4,
解得,
即,
所以直线FN的斜率为,
所以直线FN始终垂直于直线l,
因为△AFN为等腰三角形,
即|NF|=|AF|,
可得,
解得y1=±2,
则x1=0.
故l的一般式方程为x﹣y﹣2=0或x+y﹣2=0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025年高考数学考前押题卷(一)全国甲卷
注意事项:
1.本试卷满分150分,考试时间120分钟。
2.答题前,考生务必将姓名、考生号等个人信息填写在答题卡指定位置。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答。超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2025 亳州校级二模)若A={x|﹣2<x<2},,则A∩B=( )
A.{x|﹣1≤x≤2} B.{x|﹣1<x<2} C.{x|﹣2<x≤2} D.{x|﹣2≤x≤2}
2.(2025 开封模拟)已知向量,,若,则( )
A. B. C.5 D.20
3.(2025 河南校级模拟)已知的展开式中所有项的系数之和为3,则展开式中的常数项为( )
A.﹣60 B.100 C.﹣260 D.380
4.(2025 鞍山模拟)计算:( )
A. B. C. D.1
5.(2025 滨海新区三模)已知a=30.9,b=log29,c=e﹣ln3,则( )
A.b>a>c B.b>c>a C.c>a>b D.a>c>b
6.(2025 青州市校级模拟)若函数在区间(m,m+1)上不单调,则实数m的取值范围为( )
A. B. C. D.
7.(2025 江苏校级模拟)空间直角坐标系里有一点P(2,3,6),过P作一动平面m,直线l的方向向量坐标为(3,0,﹣1).当原点到m距离d最大时,下列说法正确的是( )
A.l⊥m B.l∥m C. D.d=7
8.(2025 哈尔滨校级模拟)过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
A.10 B.8 C.6 D.4
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
(多选)9.(2025 吉林四模)两批同种规格的产品,第一批占40%,次品率为3%;第二批占60%,次品率为2%,则( )
A.从两批产品中各取1件,都取到次品的概率为0.06%
B.从两批产品中各取1件,都取到次品的概率为2.4%
C.两批产品混合后任取1件,该产品是次品的概率为2.4%
D.两批产品混合后任取1件,若取到的是次品,则它取自第一批产品的概率为0.3%
(多选)10.(2025 金昌校级模拟)在△ABC中,,AB=2,BC=m,则“△ABC有唯一解”的充分条件可以是( )
A.m=1 B. C.m=2 D.
(多选)11.(2025 厦门模拟)如图,一个漏斗的上面部分可视为长方体ABCD﹣A′B′C′D′,下面部分可视为正四棱锥P﹣ABCD,O为正方形ABCD的中心,两部分的高都是该正方形边长的一半,则( )
A.A′O⊥AB B.A′O∥平面APD
C.平面AA′P⊥平面BDP D.CC′与A′P为相交直线
部选对的得6分,部分选对的得部分分,有选错的得0分.
三、填空题:本题共3小题,每小题5分,共15分.
12.(2025 哈尔滨校级模拟)已知函数,若f(a)+f(﹣1)=2,则a= .
13.(2025 青州市校级模拟)设数列{an}的前n项和为Sn,若a1=1,,则{an}的通项公式为 .
14.(2025 山海关区校级模拟)已知点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,且满足∠F1PF2=60°,若△PF1F2的外接圆面积是其内切圆面积的16倍,则该椭圆的离心率为 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(2025 江西模拟)已知△ABC是锐角三角形,角A,B,C的对边分别是a,b,c,c=2,且.
(1)求角B;
(2)求边a的取值范围.
16.(2025 南通模拟)已知数列{an}的前n项和为Sn,是首项和公差均为1的等差数列.
(1)求数列{an}的通项公式;
(2)若,求bn的最小值.
17.(2025 鞍山模拟)某校有高一学生1800人,高二学生1200人,学校采取按比例分配的分层抽样的方式从中抽取100人进行体育测试.测试后,统计得到高一样本的一分钟跳绳次数的均值为165,方差为61,高二样本的一分钟跳绳次数的均值为145,方差为31.
(1)计算总样本的一分钟跳绳次数的均值和方差;
(2)将一分钟跳绳次数≥125视为及格,整理出以下列联表:
及格 不及格 合计
高一 52 8 60
高二 38 2 40
合计 90 10 100
试根据小概率值α=0.05的独立性检验,分析一分钟跳绳次数及格情况是否与年级有关;(结果保留小数点后三位)
(3)如果将(2)表格中的所有数据都扩大为原来的10倍,在相同的检验标准下,再用独立性检验推断一分钟跳绳次数及格情况与年级之间的关联性,结果还一样吗?请你试着解释其中的原因.
附:,n=a+b+c+d.
χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
18.(2025 金昌校级模拟)如图,在四棱锥P﹣ABCD中,PA⊥平面ABD,PA=AB=4,C,D是平面ABCD内以AB为直径的半圆上的两点,且AD=2,DC∥AB.
(1)证明:BD⊥平面PAD;
(2)证明:平面PAD⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值.
19.(2025 金昌校级模拟)在以O为坐标原点的平面直角坐标系中,F(2,0)为椭圆的右焦点,过点F的直线l(斜率存在)与Z交于A,B两点,线段AB的中点为M(不与O重合),直线OM与l的斜率之积为.
(1)证明:a2=2b2;
(2)设直线OM与直线x=4交于点N,若△AFN为等腰三角形,求l的一般式方程.
2025年高考数学考前押题卷(一)全国甲卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B B C B A C D B
二.多选题(共3小题)
题号 9 10 11
答案 AC AC BCD
一.选择题(共8小题)
1.(2025 亳州校级二模)若A={x|﹣2<x<2},,则A∩B=( )
A.{x|﹣1≤x≤2} B.{x|﹣1<x<2} C.{x|﹣2<x≤2} D.{x|﹣2≤x≤2}
【解答】解:A={x|﹣2<x<2},B={x|﹣1<x≤2},
∴A∩B={x|﹣1<x<2}.
故选:B.
2.(2025 开封模拟)已知向量,,若,则( )
A. B. C.5 D.20
【解答】解:已知,,
由,得1×x﹣2×2=0,即x=4,则,
可得.
故选:B.
3.(2025 河南校级模拟)已知的展开式中所有项的系数之和为3,则展开式中的常数项为( )
A.﹣60 B.100 C.﹣260 D.380
【解答】解:的展开式中所有项的系数之和为3,
令x=1,则(1+a)×(2﹣1)6=3,故a=2,
的展开式的通项公式为:,
故的展开式中的常数项为:
.
故选:C.
4.(2025 鞍山模拟)计算:( )
A. B. C. D.1
【解答】解:原式
.
故选:B.
5.(2025 滨海新区三模)已知a=30.9,b=log29,c=e﹣ln3,则( )
A.b>a>c B.b>c>a C.c>a>b D.a>c>b
【解答】解:由题意1,1<a=30.9<31=3,b=log29>log28=3,
所以b>a>c.
故选:A.
6.(2025 青州市校级模拟)若函数在区间(m,m+1)上不单调,则实数m的取值范围为( )
A. B. C. D.
【解答】解:根据题目:函数在区间(m,m+1)上不单调,
,令,
因为函数在区间(m,m+1)上不单调,
所以y=x2﹣3在(m,m+1)上有变号零点,
即,解得.
故选:C.
7.(2025 江苏校级模拟)空间直角坐标系里有一点P(2,3,6),过P作一动平面m,直线l的方向向量坐标为(3,0,﹣1).当原点到m距离d最大时,下列说法正确的是( )
A.l⊥m B.l∥m C. D.d=7
【解答】解:由题意,原点O到m距离d最大,即OP⊥m,点P(2,3,6),
此时,故C错误,D正确.
显然是平面m的一个法向量,而直线l的方向向量,
则,
但无法确定直线l与平面m的位置关系,所以l∥m或l m,故AB错误.
故选:D.
8.(2025 哈尔滨校级模拟)过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
A.10 B.8 C.6 D.4
【解答】解:由题设知知线段AB的中点到准线的距离为4,
设A,B两点到准线的距离分别为d1,d2,
由抛物线的定义知:
|AB|=|AF|+|BF|=d1+d2=2×4=8.
故选:B.
二.多选题(共3小题)
(多选)9.(2025 吉林四模)两批同种规格的产品,第一批占40%,次品率为3%;第二批占60%,次品率为2%,则( )
A.从两批产品中各取1件,都取到次品的概率为0.06%
B.从两批产品中各取1件,都取到次品的概率为2.4%
C.两批产品混合后任取1件,该产品是次品的概率为2.4%
D.两批产品混合后任取1件,若取到的是次品,则它取自第一批产品的概率为0.3%
【解答】解:依题意,从两批产品中各取1件,都取到次品的概率为3%×2%=0.06%,故A正确,B错误;
设事件A=“从混合后的产品中取出一件是次品”,B=“次品来自第一批产品”,C=“次品来自第二批产品”,
则P(B)=40%,P(C)=60%,P(A|B)=3%,P(A|C)=2%,
所以P(A)=P(B)P(A|B)+P(C)P(A|C=40%×3%+60%×2%=2.4%,故C正确;
因为,故D错误.
故选:AC.
(多选)10.(2025 金昌校级模拟)在△ABC中,,AB=2,BC=m,则“△ABC有唯一解”的充分条件可以是( )
A.m=1 B. C.m=2 D.
【解答】解:由正弦定理,即,可得.
当m=1时,sinC=1,结合C∈(0,π),可得,△ABC唯一存在,
所以由m=1可以推出△ABC有唯一解,故A正确;
当时,,结合AB>BC,可知,
满足条件的角C有互补的两个值,相应的△ABC有两解,故B错误;
当m=2时,可得AB=BC=2,所以,则,△ABC唯一存在,
所以由m=2可以推出△ABC有唯一解,故C正确;
当时,,结合AB>BC,可得,
满足条件的角C有互补的两个值,可知△ABC有两解,D项错误.
故选:AC.
(多选)11.(2025 厦门模拟)如图,一个漏斗的上面部分可视为长方体ABCD﹣A′B′C′D′,下面部分可视为正四棱锥P﹣ABCD,O为正方形ABCD的中心,两部分的高都是该正方形边长的一半,则( )
A.A′O⊥AB B.A′O∥平面APD
C.平面AA′P⊥平面BDP D.CC′与A′P为相交直线
【解答】解:对于A,设正方形ABCD边长为2,由正四棱锥性质可得PO⊥平面ABCD,故PO=AA′=1,
因为A′A⊥面ABCD,故A′O在底面的射影为AO,
又AO不与AB垂直,故A′O不与AB垂直,故A不正确;
对于B,由题PO∥AA′且PO=AA′,故四边形POA′A是平行四边形,
所以A′O∥AP,A′O不在平面APD内,AP 平面APD,
所以A′O∥平面APD,故B正确;
对于C,因为PO∥CC′∥AA′,O∈平面CC′AA′,故PO 平面CC′A′A,
平面AA′P即为平面CC′A′A,因为A′A⊥面ABCD,BD 面ABCD,
所以A′A⊥BD,又因为BD⊥AC,A′A∩AC=A,
所以BD⊥平面CC′A′A,又BD 平面BDP,
所以平面BDP⊥平面CC′A′A,即平面AA′P⊥平面BDP,故C正确;
对于D,由C可知CC′与A′P都在平面CC′A′A中且不平行,故CC与′A′P为相交直线,故D正确.
故选:BCD.
三.填空题(共3小题)
12.(2025 哈尔滨校级模拟)已知函数,若f(a)+f(﹣1)=2,则a= 8 .
【解答】解:因为函数,f(a)+f(﹣1)=2,
所以f(﹣1)=﹣1,
故f(a)=3,即log2a=3,解得a=8.
故答案为:8.
13.(2025 青州市校级模拟)设数列{an}的前n项和为Sn,若a1=1,,则{an}的通项公式为 .
【解答】解:∵,
∴,n≥2,
两式相减得:,n≥2,
∴an+1=4an,n≥2,
又,S1=a1,∴a2=3a1=3,
∴数列{an}除去首项1后,是一个以a2=3为首项,公比为4的等比数列,
,n≥2,
∴,
故答案为:.
14.(2025 山海关区校级模拟)已知点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,且满足∠F1PF2=60°,若△PF1F2的外接圆面积是其内切圆面积的16倍,则该椭圆的离心率为 .
【解答】解:如图,点F1、F2为椭圆的左、右焦点,点P为该椭圆上一点,可知|PF1|+|PF2|=2a,且|F1F2|=2c,又∠F1PF2=60°,
利用余弦定理可知:
,
化简可得,
∴△PF1F2的面积为,
设△PF1F2的外接圆半径为R,内切圆半径为r,
由正弦定理可得,可得,
易知△PF1F2的周长为l=|PF1|+|PF2|+|F1F2|=2a+2c,
利用等面积法可知,解得,
又△PF1F2的外接圆面积是其内切圆面积的16倍,即,∴,
即可得,
∴6c=4a,离心率.
故答案为:.
四.解答题(共5小题)
15.(2025 江西模拟)已知△ABC是锐角三角形,角A,B,C的对边分别是a,b,c,c=2,且.
(1)求角B;
(2)求边a的取值范围.
【解答】解:(1)因为,c=2,
所以,
故(a﹣c)sinC=csin(A﹣B),由正弦定理可得(sinA﹣sinC)sinC=sinC×sin(A﹣B),
又sinC≠0,故得到sinA﹣sinC=sin(A﹣B),
在三角形中,sin(A+B)=sinC,
即sinA﹣sin(A+B)=sin(A﹣B),即sinA﹣sinAcosB﹣cosAsinB=sinAcosB﹣sinBcosA
整理得sinA=2sinAcosB,因为sinA≠0,故,
又B是三角形的内角,所以0<B<π,
解得;
(2)已知△ABC是锐角三角形,
所以即则①
根据余弦定理得,即,
解得b2=a2﹣2a+4,②
将②代入①中,整理得又a>0,解得1<a<4,
即a∈(1,4)
法(ii)因为△ABC是锐角三角形,c=2,
由正弦定理可得,
可得a 21,
因为,可得A,
所以tanA,可得∈(0,3),
所以a∈(1,4).
16.(2025 南通模拟)已知数列{an}的前n项和为Sn,是首项和公差均为1的等差数列.
(1)求数列{an}的通项公式;
(2)若,求bn的最小值.
【解答】解:(1)由是首项和公差均为1的等差数列,
可得1+n﹣1=n,
即有Sn=n2,
当n=1时,a1=S1=1,
当n≥2时,an=Sn﹣Sn﹣1=n2﹣(n﹣1)2=2n﹣1,
上式符合首项,
则an=2n﹣1,n∈N*;
(2)若2n﹣10n+5,
则bn+1﹣bn=2n+1﹣10(n+1)+5﹣2n+10n﹣5=2n﹣10,
当1≤n≤3时,可得b1>b2>b3>b4,
当n≥4时,bn+1﹣bn>0,即有b4<b5<b6<...<bn,
则bn的最小值为b4=16﹣35=﹣19.
17.(2025 鞍山模拟)某校有高一学生1800人,高二学生1200人,学校采取按比例分配的分层抽样的方式从中抽取100人进行体育测试.测试后,统计得到高一样本的一分钟跳绳次数的均值为165,方差为61,高二样本的一分钟跳绳次数的均值为145,方差为31.
(1)计算总样本的一分钟跳绳次数的均值和方差;
(2)将一分钟跳绳次数≥125视为及格,整理出以下列联表:
及格 不及格 合计
高一 52 8 60
高二 38 2 40
合计 90 10 100
试根据小概率值α=0.05的独立性检验,分析一分钟跳绳次数及格情况是否与年级有关;(结果保留小数点后三位)
(3)如果将(2)表格中的所有数据都扩大为原来的10倍,在相同的检验标准下,再用独立性检验推断一分钟跳绳次数及格情况与年级之间的关联性,结果还一样吗?请你试着解释其中的原因.
附:,n=a+b+c+d.
χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
【解答】解:(1)由题意可知,高一样本量为100=60,高二样本量为100=40,
所以总样本均值为,
总样本方差为;
(2)零假设为H0:一分钟跳绳次数及格情况与年级无关,
根据列联表,,
所以根据小概率值α=0.05的独立性检验,推断H0成立,即一分钟跳绳次数及格情况与年级无关;
(3)将(2)表格中的所有数据都扩大为原来的10倍,
则,
所以根据小概率值α=0.05的独立性检验,推断H0不成立,即一分钟跳绳次数及格情况与年级有关,
所以将(2)表格中的所有数据都扩大为原来的10倍,结果不一样,
因为样本量增大使得相对差异的绝对值增大,导致卡方统计量显著上升.
18.(2025 金昌校级模拟)如图,在四棱锥P﹣ABCD中,PA⊥平面ABD,PA=AB=4,C,D是平面ABCD内以AB为直径的半圆上的两点,且AD=2,DC∥AB.
(1)证明:BD⊥平面PAD;
(2)证明:平面PAD⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦值.
【解答】(1)证明:因为PA⊥平面ABD,BD 平面ABD,
所以PA⊥BD.
因为D是以AB为直径的半圆上的一点,
所以AD⊥BD,
因为PA,AD 平面PAD,PA∩AD=A,
所以BD⊥平面PAD.
(2)证明:因为BD 平面PBD,由(1)得BD⊥平面PAD,
所以平面PAD⊥平面PBD.
(3)解:以A为坐标原点,垂直于平面PAB的方向为x轴,的方向分别为y轴、z轴的正方向,
建立如图所示的空间直角坐标系A﹣xyz,
则,,
故.
设平面PBD的法向量为,
则,即,
令y=1,得,
可得 3+3﹣4=2,||2,||,
所以cos,.
设直线PC与平面PBD所成的角为θ,
所以sinθ=|cos,|.
19.(2025 金昌校级模拟)在以O为坐标原点的平面直角坐标系中,F(2,0)为椭圆的右焦点,过点F的直线l(斜率存在)与Z交于A,B两点,线段AB的中点为M(不与O重合),直线OM与l的斜率之积为.
(1)证明:a2=2b2;
(2)设直线OM与直线x=4交于点N,若△AFN为等腰三角形,求l的一般式方程.
【解答】解:(1)证明:设A(x1,y1),B(x2,y2),
因为A,B两点均在椭圆Z上,
所以,
两式相减得,
即,
设M(x0,y0),
此时x1+x2=2x0,y1+y2=2y0,
所以,
即,
则直线l的斜率,直线OM的斜率为,
所以直线OM与直线l的斜率之积为,
即,
则a2=2b2;
(2)因为椭圆的右焦点F(2,0),
所以c=2,
此时a2﹣b2=c2=4,
又a2=2b2,
解得a=2,b=2,
所以椭圆Z的方程为,
由(1)知,直线OM的方程为,
令x=4,
解得,
即,
所以直线FN的斜率为,
所以直线FN始终垂直于直线l,
因为△AFN为等腰三角形,
即|NF|=|AF|,
可得,
解得y1=±2,
则x1=0.
故l的一般式方程为x﹣y﹣2=0或x+y﹣2=0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
