期末真题演练卷(含解析)2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 期末真题演练卷(含解析)2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 11:13:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题演练卷(试题)2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2018秋 新都区期末)下列计算正确的是( )
A.a3×a2=a6 B.a3﹣a2=a C.2a+b=2ab D.﹣1﹣2=﹣3
2.(2022秋 衡东县期末)已知a=212,b=38,c=74,则a,b,c大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
3.(2024秋 永善县期末)已知,多项式a2+ma+n可因式分解为(a﹣4)(a+5),则m的值为( )
A.﹣1 B.1 C.﹣9 D.9
4.(2024秋 包河区校级期末)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.(2024秋 张家口期末)下列方程组是二元一次方程组的是( )
A. B.
C. D.
6.(2024春 铁锋区期末)某车间有120名工人生产一种如图所示的无盖正方体包装箱,已知1名工人每天可以生产200块侧面或150块底面(底面和侧面材料不同),4块侧面和1块底面正好可以做成一个无盖包装箱,应如何分配工人生产侧面或底面,才能使生产的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A.
B.
C.
D.
7.(2024秋 镇海区校级期末)已知a>b,则下列各式中一定成立的是( )
A.a﹣b<0 B.3a+1<3b+1 C.am2>bm2 D.
8.(2024秋 临漳县期末)对真命题“平行于同一条直线的两直线平行”的证明过程如图所示,则下列正确的是( )
已知:如图,a∥b,a∥c. 求证:b∥c. 证明:作直线d分别与直线a,b,c相交, ∵a∥b, ∴∠1+∠2=180°(①), ∵a∥c, ∴∠1+∠3=180°, ∴∠2=∠3, ∴b∥c(②).
A.①处为两直线平行,同位角相等
B.①处为同位角相等,两直线平行
C.②处为同位角相等,两直线平行
D.②处为两直线平行,同位角相等
二.填空题(共8小题)
9.(2023秋 渭城区期末)命题“直角三角形的两个锐角互余”是 命题.(填“真”或“假”)
10.(2024秋 宜州区期末)已知xm=6,xn=3,则x2m﹣n的值为 .
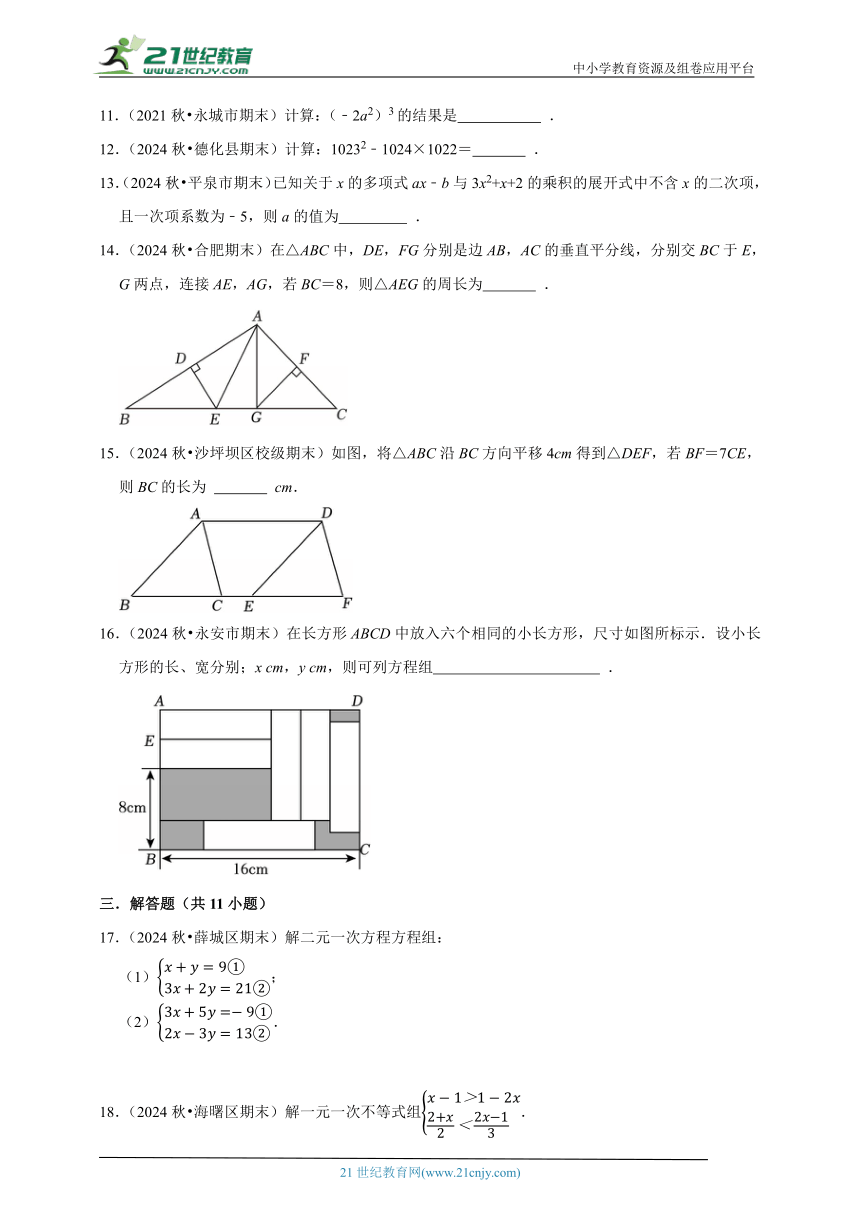
11.(2021秋 永城市期末)计算:(﹣2a2)3的结果是 .
12.(2024秋 德化县期末)计算:10232﹣1024×1022= .
13.(2024秋 平泉市期末)已知关于x的多项式ax﹣b与3x2+x+2的乘积的展开式中不含x的二次项,且一次项系数为﹣5,则a的值为 .
14.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
15.(2024秋 沙坪坝区校级期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 cm.
16.(2024秋 永安市期末)在长方形ABCD中放入六个相同的小长方形,尺寸如图所标示.设小长方形的长、宽分别;x cm,y cm,则可列方程组 .
三.解答题(共11小题)
17.(2024秋 薛城区期末)解二元一次方程方程组:
(1);
(2).
18.(2024秋 海曙区期末)解一元一次不等式组.
19.(2024秋 长宁区期末)计算:a2 a4+(﹣2a2)3+a8÷a2.
20.(2024秋 南漳县期末)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
21.(2024秋 集宁区期末)若am=an(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:
(1)如果8x=25,求x的值;
(2)如果2x+2+2x+1=24,求x的值;
(3)若x=5m﹣3,y=4﹣25m,用含x的代数式表示y.
22.(2024秋 安宁区校级期末)在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
23.(2024秋 汇川区期末)【问题情景】
数学活动课上,老师出了一个题目,阅读下列解题过程.
若x满足xy=4,x﹣y=5,求x2+y2的值.
解:∵(x﹣y)2=x2﹣2xy+y2
∴x2+y2=(x﹣y)2+2xy
=52﹣2×4
=17
【实践探究】
根据以上解题方法,解决下列问题.
若x满足(x﹣3)(x﹣8)=6
(1)请直接写出(x﹣3)﹣(x﹣8)的值为 .
(2)求(x﹣3)2+(x﹣8)2的值;
(3)将正方形ABCD和正方形EFGH按如图所示摆放,点F在BC边上,EH与CD交于点I,且ID=1,CG=2,长方形EFCI的面积为15,以CF为边作正方形CFMN.设AD=x,①则EF= ,CF= (用含x的整式直接表示).
②求图中阴影部分的面积.
24.(2024秋 岳麓区校级期末)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
25.(2024秋 沙坪坝区校级期末)如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣3,4).
(1)平移△ABC到△A1B1C1,其中点A的对应点A1的坐标为(3,1),请在图中画出△A1B1C1;B点平移后对应点的坐标为 ;
(2)请画出△ABC绕原点逆时针旋转90°得到的△A2B2C2.
(3)若△A2B2C2绕某点旋转可以得到△A1B1C1,则旋转中心的坐标为 .
26.(2024秋 临漳县期末)“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价30%进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
27.(2024秋 娄底期末)2024年度“涟商大会”在国家级地质公园湄江举行,为迎接此次盛会,某初中举办了“湄江焕彩,涟商倾情”的绘画比赛,并购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
期末真题演练卷(试题)2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B B B A C D C
一.选择题(共8小题)
1.(2018秋 新都区期末)下列计算正确的是( )
A.a3×a2=a6 B.a3﹣a2=a C.2a+b=2ab D.﹣1﹣2=﹣3
【解答】解:a3×a2=a5,故选项A不合题意;
a3与a2不是同类项,故不能合并,故选项B不合题意;
2a与b不是同类项,故不能合并,故选项C不合题意;
﹣1﹣2=﹣3,正确,故选项D符合题意.
故选:D.
2.(2022秋 衡东县期末)已知a=212,b=38,c=74,则a,b,c大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
【解答】解:a=212=84,
b=38=94,
∵9>8>7,
∴94>84>74,
∴b>a>c,
故选:B.
3.(2024秋 永善县期末)已知,多项式a2+ma+n可因式分解为(a﹣4)(a+5),则m的值为( )
A.﹣1 B.1 C.﹣9 D.9
【解答】解:根据题意可知,原式=a2+5a﹣4a﹣20=a2+a﹣20,
∵多项式可因式分解为(a﹣4)(a+5),
∴a2+ma+n=a2+a﹣20,
∴m=1,n=﹣20.
故选:B.
4.(2024秋 包河区校级期末)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是中心对称图形,不是轴对称图形,不符合题意.
D.既不是轴对称图形,也不是中心对称图形,不符合题意.
故选:B.
5.(2024秋 张家口期末)下列方程组是二元一次方程组的是( )
A. B.
C. D.
【解答】解:A.是二元一次方程组,故此选项符合题意;
B.有一个方程含有分式,不是二元一次方程组,故此选项不符合题意;
C.有一个方程的次数是2,不是二元一次方程组,故此选项不符合题意;
D.有一个方程的次数是2,不是二元一次方程组,故此选项不符合题意;
故选:A.
6.(2024春 铁锋区期末)某车间有120名工人生产一种如图所示的无盖正方体包装箱,已知1名工人每天可以生产200块侧面或150块底面(底面和侧面材料不同),4块侧面和1块底面正好可以做成一个无盖包装箱,应如何分配工人生产侧面或底面,才能使生产的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A.
B.
C.
D.
【解答】解:由题意可得,
,
故选:C.
7.(2024秋 镇海区校级期末)已知a>b,则下列各式中一定成立的是( )
A.a﹣b<0 B.3a+1<3b+1 C.am2>bm2 D.
【解答】解:A.若a>b,则a﹣b>0,故选项A不成立;
B..若a>b,则3a>3b,所以3a+1>3b+1,故选项B不成立;
C..若a>b,当m=0时,am2=bm2,故选项C不成立;
D..若a>b,则,故选项D成立.
故选:D.
8.(2024秋 临漳县期末)对真命题“平行于同一条直线的两直线平行”的证明过程如图所示,则下列正确的是( )
已知:如图,a∥b,a∥c. 求证:b∥c. 证明:作直线d分别与直线a,b,c相交, ∵a∥b, ∴∠1+∠2=180°(①), ∵a∥c, ∴∠1+∠3=180°, ∴∠2=∠3, ∴b∥c(②).
A.①处为两直线平行,同位角相等
B.①处为同位角相等,两直线平行
C.②处为同位角相等,两直线平行
D.②处为两直线平行,同位角相等
【解答】解:对真命题“平行于同一条直线的两直线平行”的证明过程如下:
证明:作直线d分别与直线a,b,c相交.
∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补)
∵a∥c,
∴∠1+∠3=180°,
∴∠2=∠3,
∴b∥c(同位角相等,两直线平行).
∴①处填两直线平行,同旁内角互补;②处填同位角相等,两直线平行.
故选:C.
二.填空题(共8小题)
9.(2023秋 渭城区期末)命题“直角三角形的两个锐角互余”是 真 命题.(填“真”或“假”)
【解答】解:命题“直角三角形的两个锐角互余”是真命题.
故答案为:真.
10.(2024秋 宜州区期末)已知xm=6,xn=3,则x2m﹣n的值为 12 .
【解答】解:x2m﹣n=(xm)2÷xn=36÷3=12.
故答案为:12.
11.(2021秋 永城市期末)计算:(﹣2a2)3的结果是 ﹣8a6 .
【解答】解:原式=﹣8a6,
故答案为:﹣8a6
12.(2024秋 德化县期末)计算:10232﹣1024×1022= 1 .
【解答】解:原式=10232﹣(1023+1)(1023﹣1)
=10232﹣10232+1
=1.
故答案为:1.
13.(2024秋 平泉市期末)已知关于x的多项式ax﹣b与3x2+x+2的乘积的展开式中不含x的二次项,且一次项系数为﹣5,则a的值为 ﹣3 .
【解答】解:根据题意可知,(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴,
解得:.
故答案为:﹣3.
14.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 8 .
【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
15.(2024秋 沙坪坝区校级期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 3 cm.
【解答】解:由平移可得,BE=CF=AD=4cm,
∵BF=BE+EF=4+(CF﹣CE)=4+4﹣CE=7CE,
∴CE=1cm,
∴BC=BE﹣CE=4﹣1=3(cm),
故答案为:3.
16.(2024秋 永安市期末)在长方形ABCD中放入六个相同的小长方形,尺寸如图所标示.设小长方形的长、宽分别;x cm,y cm,则可列方程组 .
【解答】解:依题意得:.
故答案为:.
三.解答题(共11小题)
17.(2024秋 薛城区期末)解二元一次方程方程组:
(1);
(2).
【解答】解:(1),
②×2﹣①得:x=3,
将x=3代入①得:3+y=9,
解得:y=6,
故原方程组的解为;
(2),
①×3+②×5得:19x=38,
解得:x=2,
将x=2代入②得:4﹣3y=13,
解得:y=﹣3,
故原方程组的解为.
18.(2024秋 海曙区期末)解一元一次不等式组.
【解答】解:,
解不等式①得:x,
解不等式②得:x>8,
∴原不等式组的解集为x>8.
19.(2024秋 长宁区期末)计算:a2 a4+(﹣2a2)3+a8÷a2.
【解答】解:原式=a6+(﹣8a6)+a6
=﹣6a6.
20.(2024秋 南漳县期末)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
【解答】解:∵(x+y)2=25,(x﹣y)2=9,
∴xy[(x+y)2﹣(x﹣y)2][25﹣9]=4;
x2+y2[(x+y)2+(x﹣y)2][25+9]=17.
21.(2024秋 集宁区期末)若am=an(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:
(1)如果8x=25,求x的值;
(2)如果2x+2+2x+1=24,求x的值;
(3)若x=5m﹣3,y=4﹣25m,用含x的代数式表示y.
【解答】解:(1)8x=(23)x=23x=25,
∴3x=5,
解得x;
(2)∵2x+2+2x+1=24,
∴2x(22+2)=24,
∴2x=4,
∴x=2;
(3)∵x=5m﹣3,
∴5m=x+3,
∵y=4﹣25m=4﹣(52)m
=4﹣(5m)2=4﹣(x+3)2,
∴y=﹣x2﹣6x﹣5.
22.(2024秋 安宁区校级期末)在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
【解答】解:(1)将代入②得b=﹣10,
将代入①得a=﹣1;
(2)原方程组为,
①×2﹣②得:﹣6x=32,
解得:x,
①×4+②得:30y=58,
解得:y,
即原方程组的解为:.
23.(2024秋 汇川区期末)【问题情景】
数学活动课上,老师出了一个题目,阅读下列解题过程.
若x满足xy=4,x﹣y=5,求x2+y2的值.
解:∵(x﹣y)2=x2﹣2xy+y2
∴x2+y2=(x﹣y)2+2xy
=52﹣2×4
=17
【实践探究】
根据以上解题方法,解决下列问题.
若x满足(x﹣3)(x﹣8)=6
(1)请直接写出(x﹣3)﹣(x﹣8)的值为 5 .
(2)求(x﹣3)2+(x﹣8)2的值;
(3)将正方形ABCD和正方形EFGH按如图所示摆放,点F在BC边上,EH与CD交于点I,且ID=1,CG=2,长方形EFCI的面积为15,以CF为边作正方形CFMN.设AD=x,①则EF= x﹣2 ,CF= x﹣3 (用含x的整式直接表示).
②求图中阴影部分的面积.
【解答】解:(1)(x﹣3)﹣(x﹣8)
=x﹣3﹣x+8
=5.
故答案为:5;
(2)∵(x﹣3)(x﹣8)=6,(x﹣3)﹣(x﹣8)=5,
∴原式=[(x﹣3)﹣(x﹣8)]2+2(x﹣3)(x﹣8)
=52+2×6
=37;
(3)①∵AD=x,CG=2,
∴EF=AD﹣CG=x﹣2,
又因为ID=1,CD=AD=x,
∴CF=CD﹣ID﹣CG=x﹣1﹣2=x﹣3.
故答案为:x﹣2;x﹣3;
②∵EM=EF﹣FM
=EF﹣CF
=(x﹣1)﹣(x﹣3)
=x﹣1﹣x+3
=2,
∵长方形EFCI的面积为15,
∴EF×CF=(x﹣1)(x﹣3)=15,
∴S阴影=S矩形EMNI+S矩形CGHI,
=2(x﹣3)+2(x﹣1)
=2[(x﹣3)+(x﹣1)],
∵[(x﹣3)+(x﹣1)]2=[(x﹣3)﹣(x﹣1)]2+4(x﹣3)(x﹣1)
=22+4×15
=64,
∴(x﹣3)+(x﹣1)=8,
∴S阴影=2[(x﹣3)+(x﹣1)]=2×8=16,
∴图中阴影部分的面积为16.
24.(2024秋 岳麓区校级期末)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
【解答】(1)证明:∵EF垂直平分AC,
根据线段的垂直平分线的性质可得:AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC.
(2)解:由题意可得:AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm,
∵AB=EC,BD=DE,
∴DC=DE+EC
=10cm.
25.(2024秋 沙坪坝区校级期末)如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣3,4).
(1)平移△ABC到△A1B1C1,其中点A的对应点A1的坐标为(3,1),请在图中画出△A1B1C1;B点平移后对应点的坐标为 (1,1) ;
(2)请画出△ABC绕原点逆时针旋转90°得到的△A2B2C2.
(3)若△A2B2C2绕某点旋转可以得到△A1B1C1,则旋转中心的坐标为 (2,﹣2) .
【解答】解:(1)由题意得,△ABC向右平移4个单位长度得到△A1B1C1,
如图,△A1B1C1即为所求.
由图可得,B点平移后对应点的坐标为B1(1,1).
故答案为:(1,1).
(2)如图,△A2B2C2即为所求.
(3)连接A1A2,B1B2,C1C2,分别作线段A1A2,B1B2,C1C2的垂直平分线,相交于点P,
则△A2B2C2绕点P顺时针旋转90°可以得到△A1B1C1,
∴旋转中心的坐标为(2,﹣2).
故答案为:(2,﹣2).
26.(2024秋 临漳县期末)“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价30%进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
【解答】解:(1)设一个干粉灭火器的进价为x元,一个消防自救呼吸器的进价为y元,
由题意得,,
解得:,
答:一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元.
(2)设购进干粉灭火器m个,购进消防自救呼吸器n个,
由题意得,,
解得:,
∴购进干粉灭火器60个,购进消防自救呼吸器40个,
∴全部售出后共可获利60×30%×60+10×40=1480(元),
答:全部售出后共可获利1480元.
27.(2024秋 娄底期末)2024年度“涟商大会”在国家级地质公园湄江举行,为迎接此次盛会,某初中举办了“湄江焕彩,涟商倾情”的绘画比赛,并购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题演练卷(试题)2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2018秋 新都区期末)下列计算正确的是( )
A.a3×a2=a6 B.a3﹣a2=a C.2a+b=2ab D.﹣1﹣2=﹣3
2.(2022秋 衡东县期末)已知a=212,b=38,c=74,则a,b,c大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
3.(2024秋 永善县期末)已知,多项式a2+ma+n可因式分解为(a﹣4)(a+5),则m的值为( )
A.﹣1 B.1 C.﹣9 D.9
4.(2024秋 包河区校级期末)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
5.(2024秋 张家口期末)下列方程组是二元一次方程组的是( )
A. B.
C. D.
6.(2024春 铁锋区期末)某车间有120名工人生产一种如图所示的无盖正方体包装箱,已知1名工人每天可以生产200块侧面或150块底面(底面和侧面材料不同),4块侧面和1块底面正好可以做成一个无盖包装箱,应如何分配工人生产侧面或底面,才能使生产的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A.
B.
C.
D.
7.(2024秋 镇海区校级期末)已知a>b,则下列各式中一定成立的是( )
A.a﹣b<0 B.3a+1<3b+1 C.am2>bm2 D.
8.(2024秋 临漳县期末)对真命题“平行于同一条直线的两直线平行”的证明过程如图所示,则下列正确的是( )
已知:如图,a∥b,a∥c. 求证:b∥c. 证明:作直线d分别与直线a,b,c相交, ∵a∥b, ∴∠1+∠2=180°(①), ∵a∥c, ∴∠1+∠3=180°, ∴∠2=∠3, ∴b∥c(②).
A.①处为两直线平行,同位角相等
B.①处为同位角相等,两直线平行
C.②处为同位角相等,两直线平行
D.②处为两直线平行,同位角相等
二.填空题(共8小题)
9.(2023秋 渭城区期末)命题“直角三角形的两个锐角互余”是 命题.(填“真”或“假”)
10.(2024秋 宜州区期末)已知xm=6,xn=3,则x2m﹣n的值为 .
11.(2021秋 永城市期末)计算:(﹣2a2)3的结果是 .
12.(2024秋 德化县期末)计算:10232﹣1024×1022= .
13.(2024秋 平泉市期末)已知关于x的多项式ax﹣b与3x2+x+2的乘积的展开式中不含x的二次项,且一次项系数为﹣5,则a的值为 .
14.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
15.(2024秋 沙坪坝区校级期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 cm.
16.(2024秋 永安市期末)在长方形ABCD中放入六个相同的小长方形,尺寸如图所标示.设小长方形的长、宽分别;x cm,y cm,则可列方程组 .
三.解答题(共11小题)
17.(2024秋 薛城区期末)解二元一次方程方程组:
(1);
(2).
18.(2024秋 海曙区期末)解一元一次不等式组.
19.(2024秋 长宁区期末)计算:a2 a4+(﹣2a2)3+a8÷a2.
20.(2024秋 南漳县期末)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
21.(2024秋 集宁区期末)若am=an(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:
(1)如果8x=25,求x的值;
(2)如果2x+2+2x+1=24,求x的值;
(3)若x=5m﹣3,y=4﹣25m,用含x的代数式表示y.
22.(2024秋 安宁区校级期末)在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
23.(2024秋 汇川区期末)【问题情景】
数学活动课上,老师出了一个题目,阅读下列解题过程.
若x满足xy=4,x﹣y=5,求x2+y2的值.
解:∵(x﹣y)2=x2﹣2xy+y2
∴x2+y2=(x﹣y)2+2xy
=52﹣2×4
=17
【实践探究】
根据以上解题方法,解决下列问题.
若x满足(x﹣3)(x﹣8)=6
(1)请直接写出(x﹣3)﹣(x﹣8)的值为 .
(2)求(x﹣3)2+(x﹣8)2的值;
(3)将正方形ABCD和正方形EFGH按如图所示摆放,点F在BC边上,EH与CD交于点I,且ID=1,CG=2,长方形EFCI的面积为15,以CF为边作正方形CFMN.设AD=x,①则EF= ,CF= (用含x的整式直接表示).
②求图中阴影部分的面积.
24.(2024秋 岳麓区校级期末)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
25.(2024秋 沙坪坝区校级期末)如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣3,4).
(1)平移△ABC到△A1B1C1,其中点A的对应点A1的坐标为(3,1),请在图中画出△A1B1C1;B点平移后对应点的坐标为 ;
(2)请画出△ABC绕原点逆时针旋转90°得到的△A2B2C2.
(3)若△A2B2C2绕某点旋转可以得到△A1B1C1,则旋转中心的坐标为 .
26.(2024秋 临漳县期末)“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价30%进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
27.(2024秋 娄底期末)2024年度“涟商大会”在国家级地质公园湄江举行,为迎接此次盛会,某初中举办了“湄江焕彩,涟商倾情”的绘画比赛,并购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
期末真题演练卷(试题)2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B B B A C D C
一.选择题(共8小题)
1.(2018秋 新都区期末)下列计算正确的是( )
A.a3×a2=a6 B.a3﹣a2=a C.2a+b=2ab D.﹣1﹣2=﹣3
【解答】解:a3×a2=a5,故选项A不合题意;
a3与a2不是同类项,故不能合并,故选项B不合题意;
2a与b不是同类项,故不能合并,故选项C不合题意;
﹣1﹣2=﹣3,正确,故选项D符合题意.
故选:D.
2.(2022秋 衡东县期末)已知a=212,b=38,c=74,则a,b,c大小关系是( )
A.a>b>c B.b>a>c C.c>b>a D.b>c>a
【解答】解:a=212=84,
b=38=94,
∵9>8>7,
∴94>84>74,
∴b>a>c,
故选:B.
3.(2024秋 永善县期末)已知,多项式a2+ma+n可因式分解为(a﹣4)(a+5),则m的值为( )
A.﹣1 B.1 C.﹣9 D.9
【解答】解:根据题意可知,原式=a2+5a﹣4a﹣20=a2+a﹣20,
∵多项式可因式分解为(a﹣4)(a+5),
∴a2+ma+n=a2+a﹣20,
∴m=1,n=﹣20.
故选:B.
4.(2024秋 包河区校级期末)我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,不是中心对称图形,不符合题意.
B.既是轴对称图形,又是中心对称图形,符合题意.
C.是中心对称图形,不是轴对称图形,不符合题意.
D.既不是轴对称图形,也不是中心对称图形,不符合题意.
故选:B.
5.(2024秋 张家口期末)下列方程组是二元一次方程组的是( )
A. B.
C. D.
【解答】解:A.是二元一次方程组,故此选项符合题意;
B.有一个方程含有分式,不是二元一次方程组,故此选项不符合题意;
C.有一个方程的次数是2,不是二元一次方程组,故此选项不符合题意;
D.有一个方程的次数是2,不是二元一次方程组,故此选项不符合题意;
故选:A.
6.(2024春 铁锋区期末)某车间有120名工人生产一种如图所示的无盖正方体包装箱,已知1名工人每天可以生产200块侧面或150块底面(底面和侧面材料不同),4块侧面和1块底面正好可以做成一个无盖包装箱,应如何分配工人生产侧面或底面,才能使生产的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A.
B.
C.
D.
【解答】解:由题意可得,
,
故选:C.
7.(2024秋 镇海区校级期末)已知a>b,则下列各式中一定成立的是( )
A.a﹣b<0 B.3a+1<3b+1 C.am2>bm2 D.
【解答】解:A.若a>b,则a﹣b>0,故选项A不成立;
B..若a>b,则3a>3b,所以3a+1>3b+1,故选项B不成立;
C..若a>b,当m=0时,am2=bm2,故选项C不成立;
D..若a>b,则,故选项D成立.
故选:D.
8.(2024秋 临漳县期末)对真命题“平行于同一条直线的两直线平行”的证明过程如图所示,则下列正确的是( )
已知:如图,a∥b,a∥c. 求证:b∥c. 证明:作直线d分别与直线a,b,c相交, ∵a∥b, ∴∠1+∠2=180°(①), ∵a∥c, ∴∠1+∠3=180°, ∴∠2=∠3, ∴b∥c(②).
A.①处为两直线平行,同位角相等
B.①处为同位角相等,两直线平行
C.②处为同位角相等,两直线平行
D.②处为两直线平行,同位角相等
【解答】解:对真命题“平行于同一条直线的两直线平行”的证明过程如下:
证明:作直线d分别与直线a,b,c相交.
∵a∥b,
∴∠1+∠2=180°(两直线平行,同旁内角互补)
∵a∥c,
∴∠1+∠3=180°,
∴∠2=∠3,
∴b∥c(同位角相等,两直线平行).
∴①处填两直线平行,同旁内角互补;②处填同位角相等,两直线平行.
故选:C.
二.填空题(共8小题)
9.(2023秋 渭城区期末)命题“直角三角形的两个锐角互余”是 真 命题.(填“真”或“假”)
【解答】解:命题“直角三角形的两个锐角互余”是真命题.
故答案为:真.
10.(2024秋 宜州区期末)已知xm=6,xn=3,则x2m﹣n的值为 12 .
【解答】解:x2m﹣n=(xm)2÷xn=36÷3=12.
故答案为:12.
11.(2021秋 永城市期末)计算:(﹣2a2)3的结果是 ﹣8a6 .
【解答】解:原式=﹣8a6,
故答案为:﹣8a6
12.(2024秋 德化县期末)计算:10232﹣1024×1022= 1 .
【解答】解:原式=10232﹣(1023+1)(1023﹣1)
=10232﹣10232+1
=1.
故答案为:1.
13.(2024秋 平泉市期末)已知关于x的多项式ax﹣b与3x2+x+2的乘积的展开式中不含x的二次项,且一次项系数为﹣5,则a的值为 ﹣3 .
【解答】解:根据题意可知,(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴,
解得:.
故答案为:﹣3.
14.(2024秋 合肥期末)在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 8 .
【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
15.(2024秋 沙坪坝区校级期末)如图,将△ABC沿BC方向平移4cm得到△DEF,若BF=7CE,则BC的长为 3 cm.
【解答】解:由平移可得,BE=CF=AD=4cm,
∵BF=BE+EF=4+(CF﹣CE)=4+4﹣CE=7CE,
∴CE=1cm,
∴BC=BE﹣CE=4﹣1=3(cm),
故答案为:3.
16.(2024秋 永安市期末)在长方形ABCD中放入六个相同的小长方形,尺寸如图所标示.设小长方形的长、宽分别;x cm,y cm,则可列方程组 .
【解答】解:依题意得:.
故答案为:.
三.解答题(共11小题)
17.(2024秋 薛城区期末)解二元一次方程方程组:
(1);
(2).
【解答】解:(1),
②×2﹣①得:x=3,
将x=3代入①得:3+y=9,
解得:y=6,
故原方程组的解为;
(2),
①×3+②×5得:19x=38,
解得:x=2,
将x=2代入②得:4﹣3y=13,
解得:y=﹣3,
故原方程组的解为.
18.(2024秋 海曙区期末)解一元一次不等式组.
【解答】解:,
解不等式①得:x,
解不等式②得:x>8,
∴原不等式组的解集为x>8.
19.(2024秋 长宁区期末)计算:a2 a4+(﹣2a2)3+a8÷a2.
【解答】解:原式=a6+(﹣8a6)+a6
=﹣6a6.
20.(2024秋 南漳县期末)已知(x+y)2=25,(x﹣y)2=9,求xy与x2+y2的值.
【解答】解:∵(x+y)2=25,(x﹣y)2=9,
∴xy[(x+y)2﹣(x﹣y)2][25﹣9]=4;
x2+y2[(x+y)2+(x﹣y)2][25+9]=17.
21.(2024秋 集宁区期末)若am=an(a>0且a≠1,m、n是正整数),则m=n.利用上面结论解决下面的问题:
(1)如果8x=25,求x的值;
(2)如果2x+2+2x+1=24,求x的值;
(3)若x=5m﹣3,y=4﹣25m,用含x的代数式表示y.
【解答】解:(1)8x=(23)x=23x=25,
∴3x=5,
解得x;
(2)∵2x+2+2x+1=24,
∴2x(22+2)=24,
∴2x=4,
∴x=2;
(3)∵x=5m﹣3,
∴5m=x+3,
∵y=4﹣25m=4﹣(52)m
=4﹣(5m)2=4﹣(x+3)2,
∴y=﹣x2﹣6x﹣5.
22.(2024秋 安宁区校级期末)在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
【解答】解:(1)将代入②得b=﹣10,
将代入①得a=﹣1;
(2)原方程组为,
①×2﹣②得:﹣6x=32,
解得:x,
①×4+②得:30y=58,
解得:y,
即原方程组的解为:.
23.(2024秋 汇川区期末)【问题情景】
数学活动课上,老师出了一个题目,阅读下列解题过程.
若x满足xy=4,x﹣y=5,求x2+y2的值.
解:∵(x﹣y)2=x2﹣2xy+y2
∴x2+y2=(x﹣y)2+2xy
=52﹣2×4
=17
【实践探究】
根据以上解题方法,解决下列问题.
若x满足(x﹣3)(x﹣8)=6
(1)请直接写出(x﹣3)﹣(x﹣8)的值为 5 .
(2)求(x﹣3)2+(x﹣8)2的值;
(3)将正方形ABCD和正方形EFGH按如图所示摆放,点F在BC边上,EH与CD交于点I,且ID=1,CG=2,长方形EFCI的面积为15,以CF为边作正方形CFMN.设AD=x,①则EF= x﹣2 ,CF= x﹣3 (用含x的整式直接表示).
②求图中阴影部分的面积.
【解答】解:(1)(x﹣3)﹣(x﹣8)
=x﹣3﹣x+8
=5.
故答案为:5;
(2)∵(x﹣3)(x﹣8)=6,(x﹣3)﹣(x﹣8)=5,
∴原式=[(x﹣3)﹣(x﹣8)]2+2(x﹣3)(x﹣8)
=52+2×6
=37;
(3)①∵AD=x,CG=2,
∴EF=AD﹣CG=x﹣2,
又因为ID=1,CD=AD=x,
∴CF=CD﹣ID﹣CG=x﹣1﹣2=x﹣3.
故答案为:x﹣2;x﹣3;
②∵EM=EF﹣FM
=EF﹣CF
=(x﹣1)﹣(x﹣3)
=x﹣1﹣x+3
=2,
∵长方形EFCI的面积为15,
∴EF×CF=(x﹣1)(x﹣3)=15,
∴S阴影=S矩形EMNI+S矩形CGHI,
=2(x﹣3)+2(x﹣1)
=2[(x﹣3)+(x﹣1)],
∵[(x﹣3)+(x﹣1)]2=[(x﹣3)﹣(x﹣1)]2+4(x﹣3)(x﹣1)
=22+4×15
=64,
∴(x﹣3)+(x﹣1)=8,
∴S阴影=2[(x﹣3)+(x﹣1)]=2×8=16,
∴图中阴影部分的面积为16.
24.(2024秋 岳麓区校级期末)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
【解答】(1)证明:∵EF垂直平分AC,
根据线段的垂直平分线的性质可得:AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC.
(2)解:由题意可得:AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm,
∵AB=EC,BD=DE,
∴DC=DE+EC
=10cm.
25.(2024秋 沙坪坝区校级期末)如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣3,4).
(1)平移△ABC到△A1B1C1,其中点A的对应点A1的坐标为(3,1),请在图中画出△A1B1C1;B点平移后对应点的坐标为 (1,1) ;
(2)请画出△ABC绕原点逆时针旋转90°得到的△A2B2C2.
(3)若△A2B2C2绕某点旋转可以得到△A1B1C1,则旋转中心的坐标为 (2,﹣2) .
【解答】解:(1)由题意得,△ABC向右平移4个单位长度得到△A1B1C1,
如图,△A1B1C1即为所求.
由图可得,B点平移后对应点的坐标为B1(1,1).
故答案为:(1,1).
(2)如图,△A2B2C2即为所求.
(3)连接A1A2,B1B2,C1C2,分别作线段A1A2,B1B2,C1C2的垂直平分线,相交于点P,
则△A2B2C2绕点P顺时针旋转90°可以得到△A1B1C1,
∴旋转中心的坐标为(2,﹣2).
故答案为:(2,﹣2).
26.(2024秋 临漳县期末)“预防为主,生命至上”.商场计划购进一批消防器材进行销售,已知购进15个干粉灭火器和20个消防自救呼吸器共需1500元,购进20个干粉灭火器和25个消防自救呼吸器共需1950元.
(1)求一个干粉灭火器和一个消防自救呼吸器的进价分别是多少元;
(2)该商场计划用4800元购进干粉灭火器和消防自救呼吸器共100个,销售时,干粉灭火器在进价的基础上加价30%进行销售;消防自救呼吸器每件加价10元进行销售,求全部售出后共可获利多少元.
【解答】解:(1)设一个干粉灭火器的进价为x元,一个消防自救呼吸器的进价为y元,
由题意得,,
解得:,
答:一个干粉灭火器的进价为60元,一个消防自救呼吸器的进价为30元.
(2)设购进干粉灭火器m个,购进消防自救呼吸器n个,
由题意得,,
解得:,
∴购进干粉灭火器60个,购进消防自救呼吸器40个,
∴全部售出后共可获利60×30%×60+10×40=1480(元),
答:全部售出后共可获利1480元.
27.(2024秋 娄底期末)2024年度“涟商大会”在国家级地质公园湄江举行,为迎接此次盛会,某初中举办了“湄江焕彩,涟商倾情”的绘画比赛,并购买A、B两种徽章作为奖品.已知购买2个A种徽章和3个B种徽章需156元;购买4个A种徽章和5个B种徽章需284元.
(1)每个A种徽章与每个B种徽章的价格分别为多少元?
(2)学校计划购进A、B两种徽章共60个,已知购进的A种徽章数不少于B种徽章数的2倍,且总费用不超过2000元,那么购进A种徽章的个数是多少?
【解答】解:(1)设每个A种徽章的价格为x元,每个B种徽章的价格为y元,
由题意得:,
解得:,
答:每个A种价格为36元,每个B种价格分别为28元;
(2)设购进m个A种徽章,则:
,
∴,
∴m=40,
答:购进A种徽章的个数是40.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
