期末真题演练卷(含解析)2024-2025学年数学八年级下册人教版
文档属性
| 名称 | 期末真题演练卷(含解析)2024-2025学年数学八年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 11:15:22 | ||
图片预览




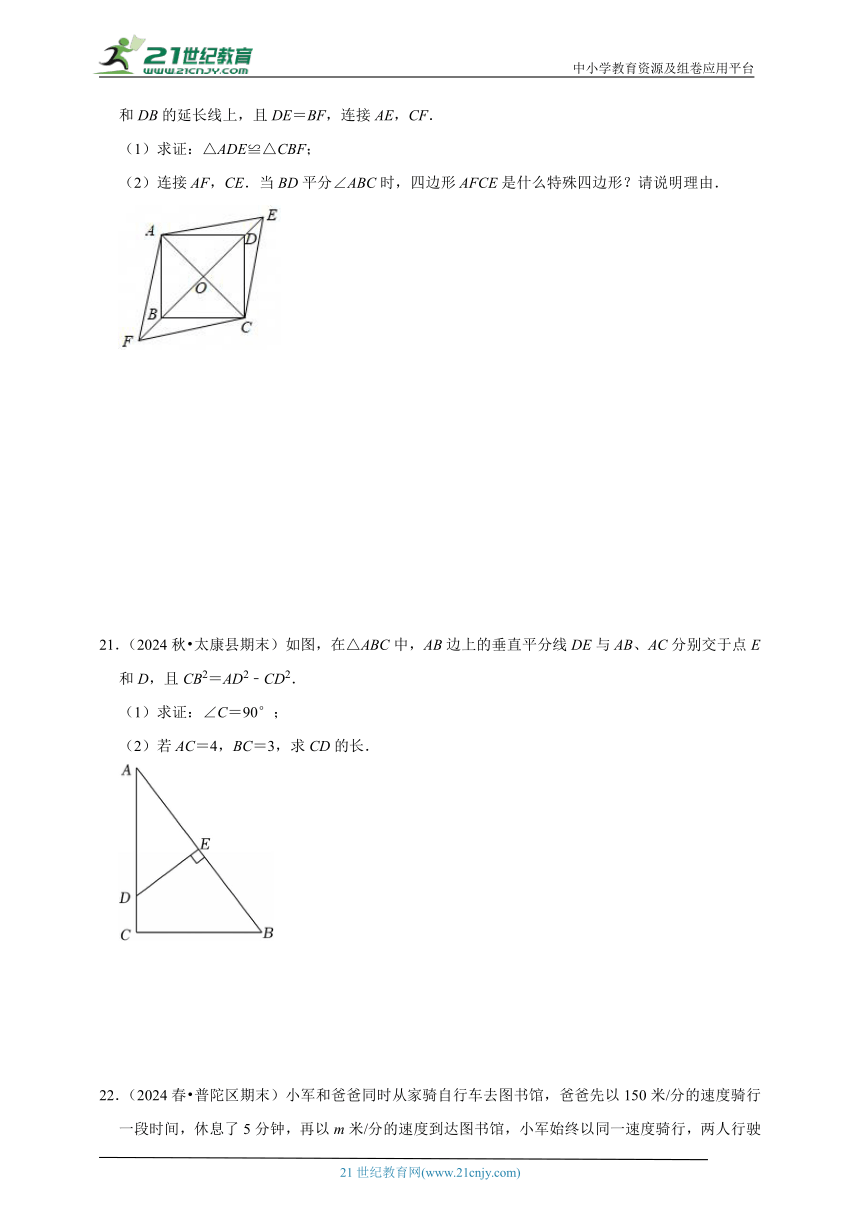
文档简介
中小学教育资源及组卷应用平台
期末真题演练卷(试题)2024-2025学年数学八年级下册人教版
一.选择题(共8小题)
1.(2024春 庄浪县期末)若式子有意义,则a的取值范围是( )
A.a>7 B.a<7 C.a≥7 D.a≤7
2.(2024秋 镇江期末)一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
3.(2024秋 龙口市期末)如图,在 ABCD中,AB=3,AD=10,AE,DF分别平分∠DAB,∠ADC,那么EF的长为( )
A.3 B.4
C.5 D.以上都不对
4.(2024春 安顺期末)甲、乙、丙、丁四个旅游团的游客人数都相等,且每个旅游团游客的平均年龄都是35岁,这四个旅游团游客年龄的方差分别是S甲2=16,S乙2=18,S丙2=5,S丁2=28,这四个旅游团中年龄差异最小的旅游团是( )
A.甲团 B.乙团 C.丙团 D.丁团
5.(2022春 交口县期末)如图(1),点P是 ABCD边上一动点,沿A→D→C→B的路径移动,设点P经过的路径长为x,△ABP的面积是y,图(2)是点P运动时y随x变化的关系图象,则AB与CD间的距离是( )
A.5 B.4 C. D.
6.(2017秋 昌平区校级期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
A.4 B.4.8 C.5 D.6
7.(2024秋 罗湖区期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=6cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=8cm,此时摆锤与静止位置时的水平距离BC=10cm时,钟摆AD的长度是( )
A.17cm B.24cm C.26cm D.28cm
8.(2024春 巩义市期末)如图,在矩形ABCD中,AB=3,作BD的垂直平分线EF,分别与AD、BC交于点E、F.连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
二.填空题(共8小题)
9.(2023春 淮北期末)若代数式在实数范围内有意义,则x的取值范围是 .
10.(2024秋 市中区期末)博物馆拟招聘一名优秀讲解员,王立的笔试、试讲、面试成绩分别为96分、90分、95分.根据实际需要,综合成绩将笔试、试讲和面试三项得分按5:3:2的比例确定最后的成绩,那么王立最后的成绩为 分.
11.(2024秋 宿迁期末)如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
12.(2024春 迎江区校级期末)已知一组数据1,3,x,5,6的平均数是x﹣1,则这组数据的方差为 .
13.(2023秋 凤翔区期末)如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .
14.(2024春 陵城区期末)已知一次函数y=(k﹣1)x+2.若当﹣1≤x≤2时,函数有最小值﹣2,则k的值为 .
15.(2024春 夏津县期末)如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= °.
16.(2024春 桑植县期末)如图,直线y1x与直线y2=kx+b相交于点A(m,2),则关于x的方程kx+b=2的解为 .
三.解答题(共10小题)
17.(2024春 呼伦贝尔期末)计算:.
18.(2024秋 金寨县期末)已知y+3与x成正比例,当x=2时,y=7.
(1)求y与x的函数表达式;
(2)当x时,求y的值.
19.(2023春 抚顺县期末)为了响应“足球进校园”的号召,更好地开展足球运动,某学校计划购买一批足球,已知购买4个A品牌足球和3个B品牌足球共需440元;购买2个A品牌足球和1个B品牌足球共需180元.
(1)求A,B两种品牌足球的单价;
(2)若学校准备购买A,B两种品牌的足球共60个,且B品牌足球数不少于A品牌足球数的2倍,设购买两种品牌足球所需总费用为y元,A品牌足球x个,求y与x之间的函数关系式,并设计一种购买方案,使所需总费用最低,并求出最低总费用.
20.(2024春 三台县期末)如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
21.(2024秋 太康县期末)如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
22.(2024春 普陀区期末)小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
23.(2024秋 东平县期末)点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
24.(2023春 重庆期末)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
25.(2024秋 大祥区期末)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,使得,,那么便有:.
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即,,
∴.
仿照上例,回答问题:
(1)计算:;
(2)计算:.
26.(2023春 宜兴市期末)在平面直角坐标系中,已知矩形OBCD,点C(4,2),现将矩形OBCD绕点O逆时针旋转(0°<∠EOB<180°)得到矩形OEFG,点B、C、D的对应点分别为点E、F、G.
(1)如图1,当点E落在边CD上时,求直线FG的函数表达式;
(2)如图2,当C、E、F三点在一直线上时,CD所在直线与OE、GF分别交于点H、M,求线段MG的长度.
(3)如图3,设点P为边FG的中点,连接PE,在矩形OBCD旋转过程中,点B到直线PE的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.
期末真题演练卷(试题)2024-2025学年数学八年级下册人教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B C A B C
一.选择题(共8小题)
1.(2024春 庄浪县期末)若式子有意义,则a的取值范围是( )
A.a>7 B.a<7 C.a≥7 D.a≤7
【解答】解:依题意得:7﹣a≥0,
解得:a≤7,
故选:D.
2.(2024秋 镇江期末)一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
【解答】解:∵k=2>0,
∴图象经过第一、三象限,
∴b=3>0,
∴图象与y轴的交点在x轴上方,
∴一次函数y=2x+3的图象经过第一、二、三象限.
故选:A.
3.(2024秋 龙口市期末)如图,在 ABCD中,AB=3,AD=10,AE,DF分别平分∠DAB,∠ADC,那么EF的长为( )
A.3 B.4
C.5 D.以上都不对
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD=3,AD=BC=10,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=BA=3,
同理CF=CD=3,
∴EF=BC﹣BE﹣CF=10﹣3﹣3=4,
故选:B.
4.(2024春 安顺期末)甲、乙、丙、丁四个旅游团的游客人数都相等,且每个旅游团游客的平均年龄都是35岁,这四个旅游团游客年龄的方差分别是S甲2=16,S乙2=18,S丙2=5,S丁2=28,这四个旅游团中年龄差异最小的旅游团是( )
A.甲团 B.乙团 C.丙团 D.丁团
【解答】解:∵S甲2=16,S乙2=18,S丙2=5,S丁2=28,
∴S丙2<S甲2<S乙2<S丁2,
∴四个旅游团中年龄差异最小的旅游团是丙旅游团,
故选:C.
5.(2022春 交口县期末)如图(1),点P是 ABCD边上一动点,沿A→D→C→B的路径移动,设点P经过的路径长为x,△ABP的面积是y,图(2)是点P运动时y随x变化的关系图象,则AB与CD间的距离是( )
A.5 B.4 C. D.
【解答】解:根据点P的运动,可得出AD=BC=6,AB=CD=10﹣6=4,
设AB与CD间的距离是d,
当点P在CD上时,y4 d=10,
解得d=5.
故选:A.
6.(2017秋 昌平区校级期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
A.4 B.4.8 C.5 D.6
【解答】解:∵在菱形ABCD中,BD=6,AC=8,
∴OBBD=3,OAAC=4,AC⊥BD,
∴AB5,
∵S菱形ABCDAC BD=AB EF,
∴EF4.8.
故选:B.
7.(2024秋 罗湖区期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=6cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=8cm,此时摆锤与静止位置时的水平距离BC=10cm时,钟摆AD的长度是( )
A.17cm B.24cm C.26cm D.28cm
【解答】解:设AB=AD=x cm,
根据题意可知,BC∥EF,CE⊥EF,BF⊥EF,BF=8cm,
∴CE=BF=8cm,
∴AC=AD+DE﹣CE=x+6﹣8=(x﹣2)cm,
在Rt△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,即x2=(x﹣2)2+102,
解得:x=26,
故选:C.
8.(2024春 巩义市期末)如图,在矩形ABCD中,AB=3,作BD的垂直平分线EF,分别与AD、BC交于点E、F.连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
【解答】解:∵四边形ABCD 为矩形,
∴OB=OD,∠A=∠ABC=90°,AD∥BC,
∴∠FBO=∠EDO,
∵∠BOF=∠DOE,
∴△BOF≌△DOE(ASA),
∴BF=DE,
∵EF垂直平分BD,
∴BE=DE,BF=DF,
∴BE=DE=BF=DF,
∴四边形BFDE为菱形,AE=CF,
∴EO=FO,∠FBO=∠OBE,∠ABE=∠OBE=∠OBF=30°,
∵EF=AE+FC,
∴AE=EO=OF=CF,
∵AB=3,
∴AE,BE,
∴CF=AE,BF=BE,
∴BC=BF+CF,
故选:B.
二.填空题(共8小题)
9.(2023春 淮北期末)若代数式在实数范围内有意义,则x的取值范围是 x≤2 .
【解答】解:∵代数式在实数范围内有意义,
∴6﹣3x≥0,即x≤2.
故答案为:x≤2.
10.(2024秋 市中区期末)博物馆拟招聘一名优秀讲解员,王立的笔试、试讲、面试成绩分别为96分、90分、95分.根据实际需要,综合成绩将笔试、试讲和面试三项得分按5:3:2的比例确定最后的成绩,那么王立最后的成绩为 94 分.
【解答】解:由题意,王立最后的成绩为(分),
故答案为:94.
11.(2024秋 宿迁期末)如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 x<2 .
【解答】解:∵一次函数y=kx+b的图象与x轴交于点A(2,0),且y随x的增大而增大,
∴当y<0时,x<2.
故答案为:x<2.
12.(2024春 迎江区校级期末)已知一组数据1,3,x,5,6的平均数是x﹣1,则这组数据的方差为 3.2 .
【解答】解:∵这一组数据1,3,x,5,6的平均数是x﹣1,
∴1+3+x+5+6=5(x﹣1),
解得x=5,
∴这组数据的平均数为x﹣1=4,
∴这组数据的方差是:[(1﹣4)2+(3﹣4)2+2×(5﹣4)2+(6﹣4)2]=3.2.
故答案为:3.2.
13.(2023秋 凤翔区期末)如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 24 .
【解答】解:在Rt△ACB中,∠ACB=90°,AC=6,BC=8,
由勾股定理得:AB10,
所以阴影部分的面积Sπ×32π×426×8 π×52=24,
故答案为:24.
14.(2024春 陵城区期末)已知一次函数y=(k﹣1)x+2.若当﹣1≤x≤2时,函数有最小值﹣2,则k的值为 5或﹣1 .
【解答】解:当k﹣1>0时,函数y随x的增大而增大,
∴当x=﹣1时,y=﹣2,
∴﹣2=﹣(k﹣1)+2,
解得:k=5;
当k﹣1<0时,函数y随x的增大而减小,
∴当x=2时,y=﹣2,
∴﹣2=2(k﹣1)+2,
解得:k=﹣1;
∴k的值为5或﹣1.
故答案为:5或﹣1.
15.(2024春 夏津县期末)如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= 60 °.
【解答】解:在Rt△ACD中,
∵点O是AC中点,
∴OD=AO,
∴∠ADO=∠CAD=20°,
∴∠DOC=40°,
∵E为BC的中点,点O是AC中点,
∴OE∥AB,
∴∠COE=∠CAB=20°,
∴∠DOE=60°,
故答案为:60.
16.(2024春 桑植县期末)如图,直线y1x与直线y2=kx+b相交于点A(m,2),则关于x的方程kx+b=2的解为 x=4 .
【解答】解:∵直线y1x与直线y2=kx+b相交于点A(m,2),
∴2m,
∴m=4,
∴P(4,2),
∴关于x的方程kx+b=2的解是x=4,
故答案为:x=4.
三.解答题(共10小题)
17.(2024春 呼伦贝尔期末)计算:.
【解答】解:
.
18.(2024秋 金寨县期末)已知y+3与x成正比例,当x=2时,y=7.
(1)求y与x的函数表达式;
(2)当x时,求y的值.
【解答】解:(1)设y+3=kx,
把x=2,y=7代入得2k=7+3,解得k=5,
所以y+3=5x,
所以y与x的函数表达式为y=5x﹣3;
(2)当x时,y=5×()﹣3.
19.(2023春 抚顺县期末)为了响应“足球进校园”的号召,更好地开展足球运动,某学校计划购买一批足球,已知购买4个A品牌足球和3个B品牌足球共需440元;购买2个A品牌足球和1个B品牌足球共需180元.
(1)求A,B两种品牌足球的单价;
(2)若学校准备购买A,B两种品牌的足球共60个,且B品牌足球数不少于A品牌足球数的2倍,设购买两种品牌足球所需总费用为y元,A品牌足球x个,求y与x之间的函数关系式,并设计一种购买方案,使所需总费用最低,并求出最低总费用.
【解答】解:(1)设A,B两种品牌足球的单价分别为a元,b元,
根据题意,得,
解得,
∴A品牌足球单价为50元,B品牌足球单价为80元.
(2)根据题意可知,B品牌足球(60﹣x)个,
∵B品牌足球不少于a品牌数的2倍,
∴60﹣x≥2x,
∴x≤20,
∴y=50x+80(60﹣x)=﹣30x+4800,
∵﹣30<0,
∴y随x的增大而减小,
∴当x=20时,y最小,此时y=﹣30×20+4800=4200.
综上,y=﹣30x+4800,y取得最小值4200元,此时A品牌足球购买了20个,B品牌足球购买了40个.
20.(2024春 三台县期末)如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)四边形AFCE是菱形,理由如下:
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴AC⊥BD,
∵△ADE≌△CBF,
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AFCE是平行四边形,
∵AC⊥BD,
∴ AFCE是菱形.
21.(2024秋 太康县期末)如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
【解答】(1)证明:连接BD,
∵AB边上的垂直平分线为DE,
∴AD=BD,
∵CB2=AD2﹣CD2,
∴CB2=BD2﹣CD2,
∴CB2+CD2=BD2,
∴∠C=90°;
(2)解:设CD=x,则AD=BD=4﹣x,
在Rt△BCD中,BD2﹣CD2=BC2,
∴(4﹣x)2﹣x2=32,
解得:x,
∴CD的长为.
22.(2024春 普陀区期末)小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= 10 b= 15 ,m= 200 ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
【解答】解:(1)1500÷150=10(分钟),
10+5=15(分钟),
(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
(2)BC段关系式为:y1=200x﹣1500,
OD段关系式为:y2=120x,
相遇时,即y1=y2,即120x=200x﹣1500
解得:x=18.75
此时:y1=y2=2250
距离图书馆:3000﹣2250=750(米)
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)当y1﹣y2=100时,解得x=20
当y2﹣y1=100时,解得x=17.5
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
23.(2024秋 东平县期末)点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
【解答】(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,ABMN,
∵MFMN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
24.(2023春 重庆期末)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= 87.5 ,b= 88 ,m= 35 ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
【解答】解:(1)八年级A、B组的频数和为20×(10%+15%)=5,
所以将八年级20名学生的成绩按从大到小排序后,第10个数和第11个数在C组,分别为87,88,
则其中位数a87.5,
七年级D组的人数为10%×20=2(人),
根据七年级成绩可知88分的最多有3人,所以众数为b=88,
∵m%=7÷20×100%=35%,
所以m=35;
故答案为:87.5,88,35;
(2)八年级的成绩更好,理由如下:
七、八年级的平均数相同,但八年级成绩的中位数和众数都比七年级的大,所以八年级的更好;
(3)500700×(1﹣10%﹣15%﹣35%)=150+280=430(人),
答:估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有430人.
25.(2024秋 大祥区期末)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,使得,,那么便有:.
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即,,
∴.
仿照上例,回答问题:
(1)计算:;
(2)计算:.
【解答】解:(1);
(2)
.
26.(2023春 宜兴市期末)在平面直角坐标系中,已知矩形OBCD,点C(4,2),现将矩形OBCD绕点O逆时针旋转(0°<∠EOB<180°)得到矩形OEFG,点B、C、D的对应点分别为点E、F、G.
(1)如图1,当点E落在边CD上时,求直线FG的函数表达式;
(2)如图2,当C、E、F三点在一直线上时,CD所在直线与OE、GF分别交于点H、M,求线段MG的长度.
(3)如图3,设点P为边FG的中点,连接PE,在矩形OBCD旋转过程中,点B到直线PE的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.
【解答】解:(1)∵矩形OBCD,点 ,
∴OB=CD=4,,∠ODC=90°,
∵矩形OEFG是由矩形OBCD旋转得到,
∴OE=OB=4,FG∥OE,
在Rt△ODE 中,,
∴DE=DO,
∴∠DOE=45°,,
∴直线OE表达式为y=x,
设FG的函数表达式为y=x+b,
由GO=DO=2,∠DOG=45° 得G(﹣2,2),
∴2=﹣2+b,
解得b=4,
∴FG的函数表达式为y=x+4;
(2)如图,过点M作MN⊥OE于N,连接OC、OF,
∵矩形OEFG是由矩形OBCD旋转得到,
∴OF=OC,∠OEF=90°,
∴FE=EC,
∵∠MNE=∠NEF=∠EFM=90°,
∴四边形MNEF是矩形,
∴MN=FE,
∴MN=EC,
∵∠MNH=∠CEH=90°,∠MHN=∠CHE,
∴△MNH≌△CEH(AAS),
∴MH=HC,
∵BC=FE=EC,OC=OC,
∴Rt△BOC≌Rt△EOC(HL),
∴∠BOC=∠EOC,
∵CD∥OB,
∴∠DCO=∠BOC=∠EOC,
∴OH=HC,
设OH=HC=m,
在 Rt△ODH 中,OD2+DH2=OH2,
∴;
解得m=3,
∴OH=CH=3,
∴EH=4﹣3=1,
∴MF=NE=2EH=2,
∴MG=4﹣MF=2;
(3)在矩形OBCD旋转过程中,点B到直线PE的距离存在最大值,这个最大值是4,理由如下:
当PE在O的左侧且PE⊥OB时,B到直线PE的距离最大,设PE于OB的交点为M,如图:
∵P为FG的中点,
∴FP=PG=2,
∴PE2,
∵S△PEOS矩形OEFG=4,
∴OM PE=4,
∴OM×24,
∴OM,
∴BM4,
∴点B到直线PE的距离最大值是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题演练卷(试题)2024-2025学年数学八年级下册人教版
一.选择题(共8小题)
1.(2024春 庄浪县期末)若式子有意义,则a的取值范围是( )
A.a>7 B.a<7 C.a≥7 D.a≤7
2.(2024秋 镇江期末)一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
3.(2024秋 龙口市期末)如图,在 ABCD中,AB=3,AD=10,AE,DF分别平分∠DAB,∠ADC,那么EF的长为( )
A.3 B.4
C.5 D.以上都不对
4.(2024春 安顺期末)甲、乙、丙、丁四个旅游团的游客人数都相等,且每个旅游团游客的平均年龄都是35岁,这四个旅游团游客年龄的方差分别是S甲2=16,S乙2=18,S丙2=5,S丁2=28,这四个旅游团中年龄差异最小的旅游团是( )
A.甲团 B.乙团 C.丙团 D.丁团
5.(2022春 交口县期末)如图(1),点P是 ABCD边上一动点,沿A→D→C→B的路径移动,设点P经过的路径长为x,△ABP的面积是y,图(2)是点P运动时y随x变化的关系图象,则AB与CD间的距离是( )
A.5 B.4 C. D.
6.(2017秋 昌平区校级期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
A.4 B.4.8 C.5 D.6
7.(2024秋 罗湖区期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=6cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=8cm,此时摆锤与静止位置时的水平距离BC=10cm时,钟摆AD的长度是( )
A.17cm B.24cm C.26cm D.28cm
8.(2024春 巩义市期末)如图,在矩形ABCD中,AB=3,作BD的垂直平分线EF,分别与AD、BC交于点E、F.连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
二.填空题(共8小题)
9.(2023春 淮北期末)若代数式在实数范围内有意义,则x的取值范围是 .
10.(2024秋 市中区期末)博物馆拟招聘一名优秀讲解员,王立的笔试、试讲、面试成绩分别为96分、90分、95分.根据实际需要,综合成绩将笔试、试讲和面试三项得分按5:3:2的比例确定最后的成绩,那么王立最后的成绩为 分.
11.(2024秋 宿迁期末)如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
12.(2024春 迎江区校级期末)已知一组数据1,3,x,5,6的平均数是x﹣1,则这组数据的方差为 .
13.(2023秋 凤翔区期末)如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .
14.(2024春 陵城区期末)已知一次函数y=(k﹣1)x+2.若当﹣1≤x≤2时,函数有最小值﹣2,则k的值为 .
15.(2024春 夏津县期末)如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= °.
16.(2024春 桑植县期末)如图,直线y1x与直线y2=kx+b相交于点A(m,2),则关于x的方程kx+b=2的解为 .
三.解答题(共10小题)
17.(2024春 呼伦贝尔期末)计算:.
18.(2024秋 金寨县期末)已知y+3与x成正比例,当x=2时,y=7.
(1)求y与x的函数表达式;
(2)当x时,求y的值.
19.(2023春 抚顺县期末)为了响应“足球进校园”的号召,更好地开展足球运动,某学校计划购买一批足球,已知购买4个A品牌足球和3个B品牌足球共需440元;购买2个A品牌足球和1个B品牌足球共需180元.
(1)求A,B两种品牌足球的单价;
(2)若学校准备购买A,B两种品牌的足球共60个,且B品牌足球数不少于A品牌足球数的2倍,设购买两种品牌足球所需总费用为y元,A品牌足球x个,求y与x之间的函数关系式,并设计一种购买方案,使所需总费用最低,并求出最低总费用.
20.(2024春 三台县期末)如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
21.(2024秋 太康县期末)如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
22.(2024春 普陀区期末)小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
23.(2024秋 东平县期末)点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
24.(2023春 重庆期末)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
25.(2024秋 大祥区期末)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,使得,,那么便有:.
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即,,
∴.
仿照上例,回答问题:
(1)计算:;
(2)计算:.
26.(2023春 宜兴市期末)在平面直角坐标系中,已知矩形OBCD,点C(4,2),现将矩形OBCD绕点O逆时针旋转(0°<∠EOB<180°)得到矩形OEFG,点B、C、D的对应点分别为点E、F、G.
(1)如图1,当点E落在边CD上时,求直线FG的函数表达式;
(2)如图2,当C、E、F三点在一直线上时,CD所在直线与OE、GF分别交于点H、M,求线段MG的长度.
(3)如图3,设点P为边FG的中点,连接PE,在矩形OBCD旋转过程中,点B到直线PE的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.
期末真题演练卷(试题)2024-2025学年数学八年级下册人教版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B C A B C
一.选择题(共8小题)
1.(2024春 庄浪县期末)若式子有意义,则a的取值范围是( )
A.a>7 B.a<7 C.a≥7 D.a≤7
【解答】解:依题意得:7﹣a≥0,
解得:a≤7,
故选:D.
2.(2024秋 镇江期末)一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
【解答】解:∵k=2>0,
∴图象经过第一、三象限,
∴b=3>0,
∴图象与y轴的交点在x轴上方,
∴一次函数y=2x+3的图象经过第一、二、三象限.
故选:A.
3.(2024秋 龙口市期末)如图,在 ABCD中,AB=3,AD=10,AE,DF分别平分∠DAB,∠ADC,那么EF的长为( )
A.3 B.4
C.5 D.以上都不对
【解答】解:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD=3,AD=BC=10,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=BA=3,
同理CF=CD=3,
∴EF=BC﹣BE﹣CF=10﹣3﹣3=4,
故选:B.
4.(2024春 安顺期末)甲、乙、丙、丁四个旅游团的游客人数都相等,且每个旅游团游客的平均年龄都是35岁,这四个旅游团游客年龄的方差分别是S甲2=16,S乙2=18,S丙2=5,S丁2=28,这四个旅游团中年龄差异最小的旅游团是( )
A.甲团 B.乙团 C.丙团 D.丁团
【解答】解:∵S甲2=16,S乙2=18,S丙2=5,S丁2=28,
∴S丙2<S甲2<S乙2<S丁2,
∴四个旅游团中年龄差异最小的旅游团是丙旅游团,
故选:C.
5.(2022春 交口县期末)如图(1),点P是 ABCD边上一动点,沿A→D→C→B的路径移动,设点P经过的路径长为x,△ABP的面积是y,图(2)是点P运动时y随x变化的关系图象,则AB与CD间的距离是( )
A.5 B.4 C. D.
【解答】解:根据点P的运动,可得出AD=BC=6,AB=CD=10﹣6=4,
设AB与CD间的距离是d,
当点P在CD上时,y4 d=10,
解得d=5.
故选:A.
6.(2017秋 昌平区校级期末)如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD于F,则EF的长为( )
A.4 B.4.8 C.5 D.6
【解答】解:∵在菱形ABCD中,BD=6,AC=8,
∴OBBD=3,OAAC=4,AC⊥BD,
∴AB5,
∵S菱形ABCDAC BD=AB EF,
∴EF4.8.
故选:B.
7.(2024秋 罗湖区期末)如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=6cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=8cm,此时摆锤与静止位置时的水平距离BC=10cm时,钟摆AD的长度是( )
A.17cm B.24cm C.26cm D.28cm
【解答】解:设AB=AD=x cm,
根据题意可知,BC∥EF,CE⊥EF,BF⊥EF,BF=8cm,
∴CE=BF=8cm,
∴AC=AD+DE﹣CE=x+6﹣8=(x﹣2)cm,
在Rt△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,即x2=(x﹣2)2+102,
解得:x=26,
故选:C.
8.(2024春 巩义市期末)如图,在矩形ABCD中,AB=3,作BD的垂直平分线EF,分别与AD、BC交于点E、F.连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.2 B.3 C.6 D.
【解答】解:∵四边形ABCD 为矩形,
∴OB=OD,∠A=∠ABC=90°,AD∥BC,
∴∠FBO=∠EDO,
∵∠BOF=∠DOE,
∴△BOF≌△DOE(ASA),
∴BF=DE,
∵EF垂直平分BD,
∴BE=DE,BF=DF,
∴BE=DE=BF=DF,
∴四边形BFDE为菱形,AE=CF,
∴EO=FO,∠FBO=∠OBE,∠ABE=∠OBE=∠OBF=30°,
∵EF=AE+FC,
∴AE=EO=OF=CF,
∵AB=3,
∴AE,BE,
∴CF=AE,BF=BE,
∴BC=BF+CF,
故选:B.
二.填空题(共8小题)
9.(2023春 淮北期末)若代数式在实数范围内有意义,则x的取值范围是 x≤2 .
【解答】解:∵代数式在实数范围内有意义,
∴6﹣3x≥0,即x≤2.
故答案为:x≤2.
10.(2024秋 市中区期末)博物馆拟招聘一名优秀讲解员,王立的笔试、试讲、面试成绩分别为96分、90分、95分.根据实际需要,综合成绩将笔试、试讲和面试三项得分按5:3:2的比例确定最后的成绩,那么王立最后的成绩为 94 分.
【解答】解:由题意,王立最后的成绩为(分),
故答案为:94.
11.(2024秋 宿迁期末)如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 x<2 .
【解答】解:∵一次函数y=kx+b的图象与x轴交于点A(2,0),且y随x的增大而增大,
∴当y<0时,x<2.
故答案为:x<2.
12.(2024春 迎江区校级期末)已知一组数据1,3,x,5,6的平均数是x﹣1,则这组数据的方差为 3.2 .
【解答】解:∵这一组数据1,3,x,5,6的平均数是x﹣1,
∴1+3+x+5+6=5(x﹣1),
解得x=5,
∴这组数据的平均数为x﹣1=4,
∴这组数据的方差是:[(1﹣4)2+(3﹣4)2+2×(5﹣4)2+(6﹣4)2]=3.2.
故答案为:3.2.
13.(2023秋 凤翔区期末)如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 24 .
【解答】解:在Rt△ACB中,∠ACB=90°,AC=6,BC=8,
由勾股定理得:AB10,
所以阴影部分的面积Sπ×32π×426×8 π×52=24,
故答案为:24.
14.(2024春 陵城区期末)已知一次函数y=(k﹣1)x+2.若当﹣1≤x≤2时,函数有最小值﹣2,则k的值为 5或﹣1 .
【解答】解:当k﹣1>0时,函数y随x的增大而增大,
∴当x=﹣1时,y=﹣2,
∴﹣2=﹣(k﹣1)+2,
解得:k=5;
当k﹣1<0时,函数y随x的增大而减小,
∴当x=2时,y=﹣2,
∴﹣2=2(k﹣1)+2,
解得:k=﹣1;
∴k的值为5或﹣1.
故答案为:5或﹣1.
15.(2024春 夏津县期末)如图,四边形ABCD中,∠ADC=90°,取AC的中点O,BC的中点E,连接OD、OE,∠CAD=∠CAB=20°,则∠DOE= 60 °.
【解答】解:在Rt△ACD中,
∵点O是AC中点,
∴OD=AO,
∴∠ADO=∠CAD=20°,
∴∠DOC=40°,
∵E为BC的中点,点O是AC中点,
∴OE∥AB,
∴∠COE=∠CAB=20°,
∴∠DOE=60°,
故答案为:60.
16.(2024春 桑植县期末)如图,直线y1x与直线y2=kx+b相交于点A(m,2),则关于x的方程kx+b=2的解为 x=4 .
【解答】解:∵直线y1x与直线y2=kx+b相交于点A(m,2),
∴2m,
∴m=4,
∴P(4,2),
∴关于x的方程kx+b=2的解是x=4,
故答案为:x=4.
三.解答题(共10小题)
17.(2024春 呼伦贝尔期末)计算:.
【解答】解:
.
18.(2024秋 金寨县期末)已知y+3与x成正比例,当x=2时,y=7.
(1)求y与x的函数表达式;
(2)当x时,求y的值.
【解答】解:(1)设y+3=kx,
把x=2,y=7代入得2k=7+3,解得k=5,
所以y+3=5x,
所以y与x的函数表达式为y=5x﹣3;
(2)当x时,y=5×()﹣3.
19.(2023春 抚顺县期末)为了响应“足球进校园”的号召,更好地开展足球运动,某学校计划购买一批足球,已知购买4个A品牌足球和3个B品牌足球共需440元;购买2个A品牌足球和1个B品牌足球共需180元.
(1)求A,B两种品牌足球的单价;
(2)若学校准备购买A,B两种品牌的足球共60个,且B品牌足球数不少于A品牌足球数的2倍,设购买两种品牌足球所需总费用为y元,A品牌足球x个,求y与x之间的函数关系式,并设计一种购买方案,使所需总费用最低,并求出最低总费用.
【解答】解:(1)设A,B两种品牌足球的单价分别为a元,b元,
根据题意,得,
解得,
∴A品牌足球单价为50元,B品牌足球单价为80元.
(2)根据题意可知,B品牌足球(60﹣x)个,
∵B品牌足球不少于a品牌数的2倍,
∴60﹣x≥2x,
∴x≤20,
∴y=50x+80(60﹣x)=﹣30x+4800,
∵﹣30<0,
∴y随x的增大而减小,
∴当x=20时,y最小,此时y=﹣30×20+4800=4200.
综上,y=﹣30x+4800,y取得最小值4200元,此时A品牌足球购买了20个,B品牌足球购买了40个.
20.(2024春 三台县期末)如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)四边形AFCE是菱形,理由如下:
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴AC⊥BD,
∵△ADE≌△CBF,
∴AE=CF,∠AED=∠CFB,
∴AE∥CF,
∴四边形AFCE是平行四边形,
∵AC⊥BD,
∴ AFCE是菱形.
21.(2024秋 太康县期末)如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
【解答】(1)证明:连接BD,
∵AB边上的垂直平分线为DE,
∴AD=BD,
∵CB2=AD2﹣CD2,
∴CB2=BD2﹣CD2,
∴CB2+CD2=BD2,
∴∠C=90°;
(2)解:设CD=x,则AD=BD=4﹣x,
在Rt△BCD中,BD2﹣CD2=BC2,
∴(4﹣x)2﹣x2=32,
解得:x,
∴CD的长为.
22.(2024春 普陀区期末)小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图象,解答下列问题:
(1)a= 10 b= 15 ,m= 200 ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
【解答】解:(1)1500÷150=10(分钟),
10+5=15(分钟),
(3000﹣1500)÷(22.5﹣15)=200(米/分).
故答案为:10;15;200.
(2)BC段关系式为:y1=200x﹣1500,
OD段关系式为:y2=120x,
相遇时,即y1=y2,即120x=200x﹣1500
解得:x=18.75
此时:y1=y2=2250
距离图书馆:3000﹣2250=750(米)
答:小军在途中与爸爸第二次相遇时,距图书馆的距离是750米.
(3)当y1﹣y2=100时,解得x=20
当y2﹣y1=100时,解得x=17.5
答:爸爸自第二次出发至到达图书馆前,17.5分钟时和20分钟时与小军相距100米.
23.(2024秋 东平县期末)点E是 ABCD的边CD上的一点,连接EA并延长,使EA=AM,连接EB并延长,使EB=BN,连接MN,F为MN的中点,连接CF,DM.
(1)求证:四边形DMFC是平行四边形;
(2)连接EF,交AB于点O,若OF=2,求EF的长.
【解答】(1)证明:∵AE=AM,EB=BN,
∴AB为△EMN的中位线,
∴AB∥MN,ABMN,
∵MFMN,
∴AB∥MF,AB=MF,
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∴MF∥CD,MF=CD,
∴四边形MFCD为平行四边形;
(2)解:连接AF,BF,则AF是△MNE的中位线,
∴AF∥EB,AF=EB,
∴四边形AFBE是平行四边形,
∴OF=OE=2,
∴EF=4.
24.(2023春 重庆期末)2023年6月5日是世界环境日,某学校举办了以“生态文明与环境保护”为主题的相关知识测试.为了了解学生对“生态文明与环境保护”相关知识的掌握情况,现从七年级和八年级参与竞赛的学生中各随机选出20名同学的成绩进行分析(单位:分,满分100分),将学生竞赛成绩分为A,B,C,D四个等级,分别是:
A:x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100.
其中,七年级学生的竞赛成绩为:
66,75,76,78,79,81,82,83,84,86,
86,88,88,88,91,92,94,95,96,96;
八年级等级C的学生成绩为:81,82,83,86,87,88,89.
两组数据的平均数、中位数、众数、方差如下表:
学生 平均数 中位数 众数 方差
七年级 85.2 86 b 59.66
八年级 85.2 a 91 91.76
根据以上信息,解答下列问题;
(1)填空:a= 87.5 ,b= 88 ,m= 35 ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由;(一条理由即可)
(3)若七年级有500名学生参赛,八年级有700名学生参赛,请估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有多少人?
【解答】解:(1)八年级A、B组的频数和为20×(10%+15%)=5,
所以将八年级20名学生的成绩按从大到小排序后,第10个数和第11个数在C组,分别为87,88,
则其中位数a87.5,
七年级D组的人数为10%×20=2(人),
根据七年级成绩可知88分的最多有3人,所以众数为b=88,
∵m%=7÷20×100%=35%,
所以m=35;
故答案为:87.5,88,35;
(2)八年级的成绩更好,理由如下:
七、八年级的平均数相同,但八年级成绩的中位数和众数都比七年级的大,所以八年级的更好;
(3)500700×(1﹣10%﹣15%﹣35%)=150+280=430(人),
答:估计两个年级参赛学生中成绩优秀(大于或等于90分)的学生共有430人.
25.(2024秋 大祥区期末)先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个数a,b,使a+b=m,ab=n,使得,,那么便有:.
例如:化简.
解:首先把化为,这里m=7,n=12,由于4+3=7,4×3=12,即,,
∴.
仿照上例,回答问题:
(1)计算:;
(2)计算:.
【解答】解:(1);
(2)
.
26.(2023春 宜兴市期末)在平面直角坐标系中,已知矩形OBCD,点C(4,2),现将矩形OBCD绕点O逆时针旋转(0°<∠EOB<180°)得到矩形OEFG,点B、C、D的对应点分别为点E、F、G.
(1)如图1,当点E落在边CD上时,求直线FG的函数表达式;
(2)如图2,当C、E、F三点在一直线上时,CD所在直线与OE、GF分别交于点H、M,求线段MG的长度.
(3)如图3,设点P为边FG的中点,连接PE,在矩形OBCD旋转过程中,点B到直线PE的距离是否存在最大值?若存在,请直接写出这个最大值;若不存在,请说明理由.
【解答】解:(1)∵矩形OBCD,点 ,
∴OB=CD=4,,∠ODC=90°,
∵矩形OEFG是由矩形OBCD旋转得到,
∴OE=OB=4,FG∥OE,
在Rt△ODE 中,,
∴DE=DO,
∴∠DOE=45°,,
∴直线OE表达式为y=x,
设FG的函数表达式为y=x+b,
由GO=DO=2,∠DOG=45° 得G(﹣2,2),
∴2=﹣2+b,
解得b=4,
∴FG的函数表达式为y=x+4;
(2)如图,过点M作MN⊥OE于N,连接OC、OF,
∵矩形OEFG是由矩形OBCD旋转得到,
∴OF=OC,∠OEF=90°,
∴FE=EC,
∵∠MNE=∠NEF=∠EFM=90°,
∴四边形MNEF是矩形,
∴MN=FE,
∴MN=EC,
∵∠MNH=∠CEH=90°,∠MHN=∠CHE,
∴△MNH≌△CEH(AAS),
∴MH=HC,
∵BC=FE=EC,OC=OC,
∴Rt△BOC≌Rt△EOC(HL),
∴∠BOC=∠EOC,
∵CD∥OB,
∴∠DCO=∠BOC=∠EOC,
∴OH=HC,
设OH=HC=m,
在 Rt△ODH 中,OD2+DH2=OH2,
∴;
解得m=3,
∴OH=CH=3,
∴EH=4﹣3=1,
∴MF=NE=2EH=2,
∴MG=4﹣MF=2;
(3)在矩形OBCD旋转过程中,点B到直线PE的距离存在最大值,这个最大值是4,理由如下:
当PE在O的左侧且PE⊥OB时,B到直线PE的距离最大,设PE于OB的交点为M,如图:
∵P为FG的中点,
∴FP=PG=2,
∴PE2,
∵S△PEOS矩形OEFG=4,
∴OM PE=4,
∴OM×24,
∴OM,
∴BM4,
∴点B到直线PE的距离最大值是4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
