期末应用题易错精选题:圆柱和圆锥(含答案)-2024-2025学年数学六年级下册人教版
文档属性
| 名称 | 期末应用题易错精选题:圆柱和圆锥(含答案)-2024-2025学年数学六年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 05:20:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册人教版
1.(2024春 交城县期末)淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
2.(2024春 西乡县期末)将两个体积是12立方米的圆柱体钢锭熔铸成一个底面积是36平方米的圆锥形钢锭,这个圆锥形钢锭的高是多少米?
3.(2024春 播州区期末)如图,把两个同样大小的小圆柱拼成一个大圆柱,表面积减少6.28cm2,然后把新的圆柱沿直径截成两个半圆柱,表面积又增加80cm2,原来每个小圆柱的体积是多少立方厘米?
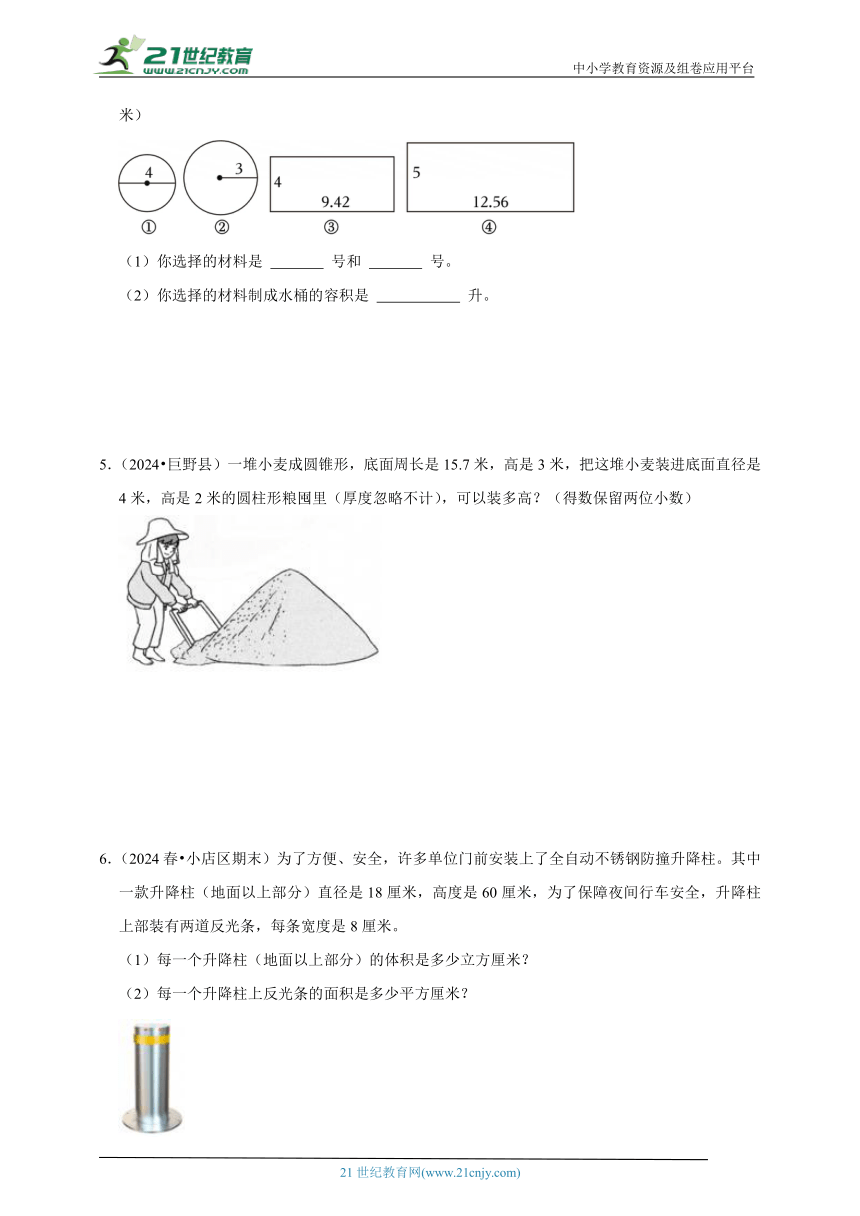
4.(2024 姑苏区)要制作一个无盖圆柱形水桶,有如图几种型号的铁皮可以供搭配选择。(单位:分米)
(1)你选择的材料是 号和 号。
(2)你选择的材料制成水桶的容积是 升。
5.(2024 巨野县)一堆小麦成圆锥形,底面周长是15.7米,高是3米,把这堆小麦装进底面直径是4米,高是2米的圆柱形粮囤里(厚度忽略不计),可以装多高?(得数保留两位小数)
6.(2024春 小店区期末)为了方便、安全,许多单位门前安装上了全自动不锈钢防撞升降柱。其中一款升降柱(地面以上部分)直径是18厘米,高度是60厘米,为了保障夜间行车安全,升降柱上部装有两道反光条,每条宽度是8厘米。
(1)每一个升降柱(地面以上部分)的体积是多少立方厘米?
(2)每一个升降柱上反光条的面积是多少平方厘米?
7.(2024 湖里区)有块正方体的木料,它的棱长是4dm.把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
8.(2024春 山亭区期末)小亮到小芳家做客,小芳拿出了如图所示的一个上半部分是圆锥形的玻璃杯和一瓶圆柱形罐装饮料招待小亮。(单位:厘米)
(1)图中圆锥形玻璃杯的容积约多少立方厘米?
(2)每罐饮料大约能倒这样的玻璃杯几杯?
(3)制作一个饮料罐至少需要多少平方厘米的材料?
9.(2024 渝中区)一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少cm2?
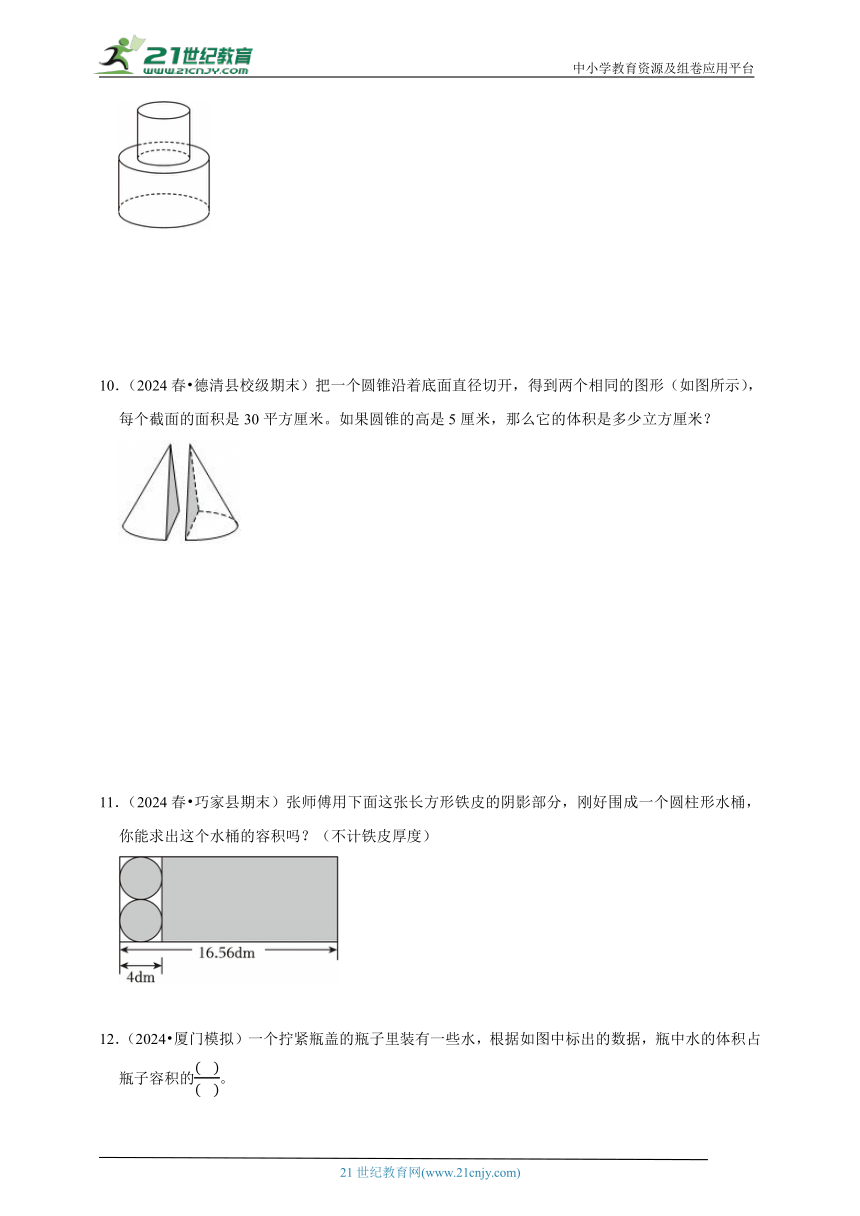
10.(2024春 德清县校级期末)把一个圆锥沿着底面直径切开,得到两个相同的图形(如图所示),每个截面的面积是30平方厘米。如果圆锥的高是5厘米,那么它的体积是多少立方厘米?
11.(2024春 巧家县期末)张师傅用下面这张长方形铁皮的阴影部分,刚好围成一个圆柱形水桶,你能求出这个水桶的容积吗?(不计铁皮厚度)
12.(2024 厦门模拟)一个拧紧瓶盖的瓶子里装有一些水,根据如图中标出的数据,瓶中水的体积占瓶子容积的。
13.(2024春 泗水县期末)如图中,挖去中间的圆柱后,剩下部分的体积是多少立方厘米?(单位:厘米)
14.(2024 思明区)北京冬奥会U型场地设在张家口赛区,其场地如一个横着的半圆柱(如图所示),全长160米,雪槽深度6米。
(1)要建一个这样的滑雪U型池,需要挖出多少立方米的泥土?
(2)施工人员想在滑雪U型池的底部铺上旱冰,需要铺多少平方米的旱冰?
15.(2024 秦都区)如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 cm,匀速注水的水流速度为 cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
16.(2024春 高新区期末)如图,沙漏是由两个完全相同的圆锥形容器组成的,单个圆锥形容器的底面直径是8cm,高为9cm。
给上面的圆锥形容器装满细沙,如果每分钟向下漏2.5cm3,那么这些沙子全部漏完大约需要多少分钟?(结果保留整数)
17.(2024春 高新区期末)一个圆柱形容器,从里面量,高12厘米,底面半径10厘米,水深3厘米。把一个棱长8厘米的正方体铁块放入水中,正方体的一个面与圆柱的底面贴合,这时水深多少厘米?(结果保留一位小数)
18.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
19.(2024 历城区)一个圆柱形木块按图甲的方式切成形状、大小相同的四块,表面积增加了600cm2;按图乙的方式切成形状、大小相同的三块,表面积增加了314cm2。求这根木料的体积。
20.(2024 临朐县)做实验想问题。
步骤1:准备一个底面积是10平方厘米的圆柱形空水杯。
步骤2:放入一个底面积是8平方厘米、高是6厘米的圆锥形铁块。
步骤3:向水杯里倒水,水面没过铁块即可。(不倒满)
步骤4:取出铁块,水面下降。
你能算出水面下降了多少厘米吗?
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册人教版
参考答案与试题解析
一.解答题(共20小题)
1.(2024春 交城县期末)淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
【解答】解:(1)3×(2.4÷2)2×9.5
=3×1.44×9.5
=4.32×9.5
≈41(立方厘米)
答:50枚一元硬币的体积约是41立方厘米。
(2)41÷50=0.82(立方厘米)
答:1枚一元硬币的体积是0.82立方厘米。
2.(2024春 西乡县期末)将两个体积是12立方米的圆柱体钢锭熔铸成一个底面积是36平方米的圆锥形钢锭,这个圆锥形钢锭的高是多少米?
【解答】解:12×2×3÷36,
=72÷36,
=2(米);
答:这个圆锥形钢锭的高是2米.
3.(2024春 播州区期末)如图,把两个同样大小的小圆柱拼成一个大圆柱,表面积减少6.28cm2,然后把新的圆柱沿直径截成两个半圆柱,表面积又增加80cm2,原来每个小圆柱的体积是多少立方厘米?
【解答】解:6.28÷2=3.14(cm2)
3.14÷3.14=1(cm2)
1=1×1,即两个同样大小的小圆柱底面半径是1cm。
1×2=2(cm),即两个同样大小的小圆柱底面直径是2cm。
80÷2=40(cm2)
40÷2=20(cm)
20÷2=10(cm)
3.14×12×10=31.4(cm3)
答:原来每个小圆柱的体积是31.4立方厘米。
4.(2024 姑苏区)要制作一个无盖圆柱形水桶,有如图几种型号的铁皮可以供搭配选择。(单位:分米)
(1)你选择的材料是 ① 号和 ④ 号。
(2)你选择的材料制成水桶的容积是 62.8 升。
【解答】解:(1)选择直径4分米的圆作为底面,长12.56分米,宽5分米的长方形作为侧面围成一个无盖的圆柱形水桶。
答:选择的材料是①和④。
(2)3.14×(4÷2)2×5
=3.14×4×5
=62.8(立方分米)
=62.8(升)
答:制成水桶的容积是62.8升。
故答案为:(1)①、④;(2)62.8。
5.(2024 巨野县)一堆小麦成圆锥形,底面周长是15.7米,高是3米,把这堆小麦装进底面直径是4米,高是2米的圆柱形粮囤里(厚度忽略不计),可以装多高?(得数保留两位小数)
【解答】解:15.7÷3.14÷2=2.5(米)
3.14×2.52×3÷[3.14×(4÷2)2]
3.14×6.25×3÷[3.14×4]
=19.625÷12.56
≈1.56(米)
答:大约可以装1.56米高。
6.(2024春 小店区期末)为了方便、安全,许多单位门前安装上了全自动不锈钢防撞升降柱。其中一款升降柱(地面以上部分)直径是18厘米,高度是60厘米,为了保障夜间行车安全,升降柱上部装有两道反光条,每条宽度是8厘米。
(1)每一个升降柱(地面以上部分)的体积是多少立方厘米?
(2)每一个升降柱上反光条的面积是多少平方厘米?
【解答】解:(1)18÷2=9(厘米)
3.14×9×9×60=15260.4(立方厘米)
答:每一个升降柱(地面以上部分)的体积是15260.4立方厘米。
(2)18×3.14×8×2=904.32(平方厘米)
答:每一个升降柱上反光条的面积是904.32平方厘米。
7.(2024 湖里区)有块正方体的木料,它的棱长是4dm.把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
【解答】解:3.14×(4÷2)2×4,
=3.14×4×4,
=50.24(立方分米);
答:这个圆柱的体积是50.24立方分米,
8.(2024春 山亭区期末)小亮到小芳家做客,小芳拿出了如图所示的一个上半部分是圆锥形的玻璃杯和一瓶圆柱形罐装饮料招待小亮。(单位:厘米)
(1)图中圆锥形玻璃杯的容积约多少立方厘米?
(2)每罐饮料大约能倒这样的玻璃杯几杯?
(3)制作一个饮料罐至少需要多少平方厘米的材料?
【解答】解:(1)3.14×(10÷2)×(10÷2)×6÷3
=471÷3
=157(立方厘米)
答:图中圆锥形玻璃杯的容积约157立方厘米。
(2)3.14×(8÷2)×(8÷2)×20÷157
=1004.8÷157
≈6(杯)
答:每罐饮料大约能倒这样的玻璃杯6杯。
(3)3.14×8×20+3.14×(8÷2)×(8÷2)×2
=502.4+100.48
=602.88(平方厘米)
答:制作一个饮料罐至少需要602.88平方厘米的材料。
9.(2024 渝中区)一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少cm2?
【解答】解:2×3.14×4×10+2×3.14×8×10+3.14×82×2
=25.12×10+50.24×10+3.14×64×2
=251.2+502.4+401.92
=1155.52(平方厘米)
答:涂色部分共1155.52平方厘米。
10.(2024春 德清县校级期末)把一个圆锥沿着底面直径切开,得到两个相同的图形(如图所示),每个截面的面积是30平方厘米。如果圆锥的高是5厘米,那么它的体积是多少立方厘米?
【解答】解:30×2÷5
=60÷5
=12(厘米)
3.14×(12÷2)×(12÷2)×5÷3
=3.14×36×5÷3
=565.2÷3
=188.4(立方厘米)
答:它的体积是188.4立方厘米。
11.(2024春 巧家县期末)张师傅用下面这张长方形铁皮的阴影部分,刚好围成一个圆柱形水桶,你能求出这个水桶的容积吗?(不计铁皮厚度)
【解答】解:3.14×(4÷2)2×(4×2)
=3.14×4×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:这个水桶的容积是100.48升。
12.(2024 厦门模拟)一个拧紧瓶盖的瓶子里装有一些水,根据如图中标出的数据,瓶中水的体积占瓶子容积的。
【解答】解:12÷(20﹣15+12)
=12÷17
答:瓶中水的体积占瓶子容积的。
故答案为:。
13.(2024春 泗水县期末)如图中,挖去中间的圆柱后,剩下部分的体积是多少立方厘米?(单位:厘米)
【解答】解:20×20×30﹣3.14×(20÷2)2×30
=12000﹣9420
=2580(立方厘米)
答:剩下部分的体积是2580立方厘米。
14.(2024 思明区)北京冬奥会U型场地设在张家口赛区,其场地如一个横着的半圆柱(如图所示),全长160米,雪槽深度6米。
(1)要建一个这样的滑雪U型池,需要挖出多少立方米的泥土?
(2)施工人员想在滑雪U型池的底部铺上旱冰,需要铺多少平方米的旱冰?
【解答】解:(1)3.14×62×160÷2
=3.14×36×160÷2
=113.04×160÷2
=18086.4÷2
=9043.2(立方米)
答:需要挖出9043.2分米泥土。
(2)2×3.14×6×160÷2
=37.68×160÷2
=6028.8÷2
=3014.4(平方米)
答:需要铺旱冰的面积是3014.4平方米。
15.(2024 秦都区)如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 14 cm,匀速注水的水流速度为 5 cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
【解答】解:(1)根据水面高度h(cm)与注水时间t(s)之间的关系,
可得圆柱形容器的高为14cm,
30×(14﹣11)÷(42﹣24)
=30×3÷18
=90÷18
=5(cm3/s)
所以匀速注水的水流速度为5cm3/s.
答:圆柱形容器的高为14cm,匀速注水的水流速度为5cm3/s.
(2)“几何体”上方圆柱的高为:
11﹣(5×18)÷(30﹣15)
=11﹣90÷15
=11﹣6
=5(cm)
设“几何体”上方圆柱的底面积为scm2,
则5 (30﹣s)=5×(24﹣18),
150﹣5s=30
150﹣5s+5s=30+5s
30+5s=150
30+5s﹣30=150﹣30
5s=120
5s÷5=120÷5
s=24
所以“几何体”上方圆柱的底面积为24cm2.
答:“几何体”上方圆柱的高为5cm,底面积为24cm2.
故答案为:14,5.
16.(2024春 高新区期末)如图,沙漏是由两个完全相同的圆锥形容器组成的,单个圆锥形容器的底面直径是8cm,高为9cm。
给上面的圆锥形容器装满细沙,如果每分钟向下漏2.5cm3,那么这些沙子全部漏完大约需要多少分钟?(结果保留整数)
【解答】解:3.14×(8÷2)2×92.5
=3.14×16×92.5
=452.162.5
≈60(分钟)
答:这些沙子全部漏完大约需要60分钟。
17.(2024春 高新区期末)一个圆柱形容器,从里面量,高12厘米,底面半径10厘米,水深3厘米。把一个棱长8厘米的正方体铁块放入水中,正方体的一个面与圆柱的底面贴合,这时水深多少厘米?(结果保留一位小数)
【解答】解:8×8×3÷(3.14×102﹣8×8)+3
=64×3÷(3.14×100﹣64)+3
=192÷(314﹣64)+3
=192÷250+3
≈0.8+3
=3.8(厘米)
答:这时水深约3.8厘米。
18.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
【解答】解:(2×3+3.14×2)×10,
=(6+6.28)×10,
=12.28×10,
=122.8(平方厘米);
答:至少需要122.8平方厘米的纸.
19.(2024 历城区)一个圆柱形木块按图甲的方式切成形状、大小相同的四块,表面积增加了600cm2;按图乙的方式切成形状、大小相同的三块,表面积增加了314cm2。求这根木料的体积。
【解答】解:600÷4=150(cm2)
即圆柱底面直径和高的乘积为150cm2。
314÷4=78.5(cm2)
78.5÷3.14=25(cm2)
25=5×5,即圆柱底面半径是5cm。
5×2=10(cm),即圆柱底面直径是10cm。
150÷10=15(cm),即圆柱高是15cm。
3.14×25×15=1177.5(cm3)
答:这根木料的体积是1177.5cm3。
20.(2024 临朐县)做实验想问题。
步骤1:准备一个底面积是10平方厘米的圆柱形空水杯。
步骤2:放入一个底面积是8平方厘米、高是6厘米的圆锥形铁块。
步骤3:向水杯里倒水,水面没过铁块即可。(不倒满)
步骤4:取出铁块,水面下降。
你能算出水面下降了多少厘米吗?
【解答】解:8×610
=16÷10
=1.6(厘米)
答:水面下降了1.6厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册人教版
1.(2024春 交城县期末)淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
2.(2024春 西乡县期末)将两个体积是12立方米的圆柱体钢锭熔铸成一个底面积是36平方米的圆锥形钢锭,这个圆锥形钢锭的高是多少米?
3.(2024春 播州区期末)如图,把两个同样大小的小圆柱拼成一个大圆柱,表面积减少6.28cm2,然后把新的圆柱沿直径截成两个半圆柱,表面积又增加80cm2,原来每个小圆柱的体积是多少立方厘米?
4.(2024 姑苏区)要制作一个无盖圆柱形水桶,有如图几种型号的铁皮可以供搭配选择。(单位:分米)
(1)你选择的材料是 号和 号。
(2)你选择的材料制成水桶的容积是 升。
5.(2024 巨野县)一堆小麦成圆锥形,底面周长是15.7米,高是3米,把这堆小麦装进底面直径是4米,高是2米的圆柱形粮囤里(厚度忽略不计),可以装多高?(得数保留两位小数)
6.(2024春 小店区期末)为了方便、安全,许多单位门前安装上了全自动不锈钢防撞升降柱。其中一款升降柱(地面以上部分)直径是18厘米,高度是60厘米,为了保障夜间行车安全,升降柱上部装有两道反光条,每条宽度是8厘米。
(1)每一个升降柱(地面以上部分)的体积是多少立方厘米?
(2)每一个升降柱上反光条的面积是多少平方厘米?
7.(2024 湖里区)有块正方体的木料,它的棱长是4dm.把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
8.(2024春 山亭区期末)小亮到小芳家做客,小芳拿出了如图所示的一个上半部分是圆锥形的玻璃杯和一瓶圆柱形罐装饮料招待小亮。(单位:厘米)
(1)图中圆锥形玻璃杯的容积约多少立方厘米?
(2)每罐饮料大约能倒这样的玻璃杯几杯?
(3)制作一个饮料罐至少需要多少平方厘米的材料?
9.(2024 渝中区)一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少cm2?
10.(2024春 德清县校级期末)把一个圆锥沿着底面直径切开,得到两个相同的图形(如图所示),每个截面的面积是30平方厘米。如果圆锥的高是5厘米,那么它的体积是多少立方厘米?
11.(2024春 巧家县期末)张师傅用下面这张长方形铁皮的阴影部分,刚好围成一个圆柱形水桶,你能求出这个水桶的容积吗?(不计铁皮厚度)
12.(2024 厦门模拟)一个拧紧瓶盖的瓶子里装有一些水,根据如图中标出的数据,瓶中水的体积占瓶子容积的。
13.(2024春 泗水县期末)如图中,挖去中间的圆柱后,剩下部分的体积是多少立方厘米?(单位:厘米)
14.(2024 思明区)北京冬奥会U型场地设在张家口赛区,其场地如一个横着的半圆柱(如图所示),全长160米,雪槽深度6米。
(1)要建一个这样的滑雪U型池,需要挖出多少立方米的泥土?
(2)施工人员想在滑雪U型池的底部铺上旱冰,需要铺多少平方米的旱冰?
15.(2024 秦都区)如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 cm,匀速注水的水流速度为 cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
16.(2024春 高新区期末)如图,沙漏是由两个完全相同的圆锥形容器组成的,单个圆锥形容器的底面直径是8cm,高为9cm。
给上面的圆锥形容器装满细沙,如果每分钟向下漏2.5cm3,那么这些沙子全部漏完大约需要多少分钟?(结果保留整数)
17.(2024春 高新区期末)一个圆柱形容器,从里面量,高12厘米,底面半径10厘米,水深3厘米。把一个棱长8厘米的正方体铁块放入水中,正方体的一个面与圆柱的底面贴合,这时水深多少厘米?(结果保留一位小数)
18.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
19.(2024 历城区)一个圆柱形木块按图甲的方式切成形状、大小相同的四块,表面积增加了600cm2;按图乙的方式切成形状、大小相同的三块,表面积增加了314cm2。求这根木料的体积。
20.(2024 临朐县)做实验想问题。
步骤1:准备一个底面积是10平方厘米的圆柱形空水杯。
步骤2:放入一个底面积是8平方厘米、高是6厘米的圆锥形铁块。
步骤3:向水杯里倒水,水面没过铁块即可。(不倒满)
步骤4:取出铁块,水面下降。
你能算出水面下降了多少厘米吗?
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册人教版
参考答案与试题解析
一.解答题(共20小题)
1.(2024春 交城县期末)淘气用下面的方法测量1枚一元硬币的体积。
(1)算一算50枚一元硬币摞起来(如图),它的体积是多少?(π取3来计算,得数保留整数)
(2)1枚一元硬币的体积是多大?
【解答】解:(1)3×(2.4÷2)2×9.5
=3×1.44×9.5
=4.32×9.5
≈41(立方厘米)
答:50枚一元硬币的体积约是41立方厘米。
(2)41÷50=0.82(立方厘米)
答:1枚一元硬币的体积是0.82立方厘米。
2.(2024春 西乡县期末)将两个体积是12立方米的圆柱体钢锭熔铸成一个底面积是36平方米的圆锥形钢锭,这个圆锥形钢锭的高是多少米?
【解答】解:12×2×3÷36,
=72÷36,
=2(米);
答:这个圆锥形钢锭的高是2米.
3.(2024春 播州区期末)如图,把两个同样大小的小圆柱拼成一个大圆柱,表面积减少6.28cm2,然后把新的圆柱沿直径截成两个半圆柱,表面积又增加80cm2,原来每个小圆柱的体积是多少立方厘米?
【解答】解:6.28÷2=3.14(cm2)
3.14÷3.14=1(cm2)
1=1×1,即两个同样大小的小圆柱底面半径是1cm。
1×2=2(cm),即两个同样大小的小圆柱底面直径是2cm。
80÷2=40(cm2)
40÷2=20(cm)
20÷2=10(cm)
3.14×12×10=31.4(cm3)
答:原来每个小圆柱的体积是31.4立方厘米。
4.(2024 姑苏区)要制作一个无盖圆柱形水桶,有如图几种型号的铁皮可以供搭配选择。(单位:分米)
(1)你选择的材料是 ① 号和 ④ 号。
(2)你选择的材料制成水桶的容积是 62.8 升。
【解答】解:(1)选择直径4分米的圆作为底面,长12.56分米,宽5分米的长方形作为侧面围成一个无盖的圆柱形水桶。
答:选择的材料是①和④。
(2)3.14×(4÷2)2×5
=3.14×4×5
=62.8(立方分米)
=62.8(升)
答:制成水桶的容积是62.8升。
故答案为:(1)①、④;(2)62.8。
5.(2024 巨野县)一堆小麦成圆锥形,底面周长是15.7米,高是3米,把这堆小麦装进底面直径是4米,高是2米的圆柱形粮囤里(厚度忽略不计),可以装多高?(得数保留两位小数)
【解答】解:15.7÷3.14÷2=2.5(米)
3.14×2.52×3÷[3.14×(4÷2)2]
3.14×6.25×3÷[3.14×4]
=19.625÷12.56
≈1.56(米)
答:大约可以装1.56米高。
6.(2024春 小店区期末)为了方便、安全,许多单位门前安装上了全自动不锈钢防撞升降柱。其中一款升降柱(地面以上部分)直径是18厘米,高度是60厘米,为了保障夜间行车安全,升降柱上部装有两道反光条,每条宽度是8厘米。
(1)每一个升降柱(地面以上部分)的体积是多少立方厘米?
(2)每一个升降柱上反光条的面积是多少平方厘米?
【解答】解:(1)18÷2=9(厘米)
3.14×9×9×60=15260.4(立方厘米)
答:每一个升降柱(地面以上部分)的体积是15260.4立方厘米。
(2)18×3.14×8×2=904.32(平方厘米)
答:每一个升降柱上反光条的面积是904.32平方厘米。
7.(2024 湖里区)有块正方体的木料,它的棱长是4dm.把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
【解答】解:3.14×(4÷2)2×4,
=3.14×4×4,
=50.24(立方分米);
答:这个圆柱的体积是50.24立方分米,
8.(2024春 山亭区期末)小亮到小芳家做客,小芳拿出了如图所示的一个上半部分是圆锥形的玻璃杯和一瓶圆柱形罐装饮料招待小亮。(单位:厘米)
(1)图中圆锥形玻璃杯的容积约多少立方厘米?
(2)每罐饮料大约能倒这样的玻璃杯几杯?
(3)制作一个饮料罐至少需要多少平方厘米的材料?
【解答】解:(1)3.14×(10÷2)×(10÷2)×6÷3
=471÷3
=157(立方厘米)
答:图中圆锥形玻璃杯的容积约157立方厘米。
(2)3.14×(8÷2)×(8÷2)×20÷157
=1004.8÷157
≈6(杯)
答:每罐饮料大约能倒这样的玻璃杯6杯。
(3)3.14×8×20+3.14×(8÷2)×(8÷2)×2
=502.4+100.48
=602.88(平方厘米)
答:制作一个饮料罐至少需要602.88平方厘米的材料。
9.(2024 渝中区)一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少cm2?
【解答】解:2×3.14×4×10+2×3.14×8×10+3.14×82×2
=25.12×10+50.24×10+3.14×64×2
=251.2+502.4+401.92
=1155.52(平方厘米)
答:涂色部分共1155.52平方厘米。
10.(2024春 德清县校级期末)把一个圆锥沿着底面直径切开,得到两个相同的图形(如图所示),每个截面的面积是30平方厘米。如果圆锥的高是5厘米,那么它的体积是多少立方厘米?
【解答】解:30×2÷5
=60÷5
=12(厘米)
3.14×(12÷2)×(12÷2)×5÷3
=3.14×36×5÷3
=565.2÷3
=188.4(立方厘米)
答:它的体积是188.4立方厘米。
11.(2024春 巧家县期末)张师傅用下面这张长方形铁皮的阴影部分,刚好围成一个圆柱形水桶,你能求出这个水桶的容积吗?(不计铁皮厚度)
【解答】解:3.14×(4÷2)2×(4×2)
=3.14×4×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:这个水桶的容积是100.48升。
12.(2024 厦门模拟)一个拧紧瓶盖的瓶子里装有一些水,根据如图中标出的数据,瓶中水的体积占瓶子容积的。
【解答】解:12÷(20﹣15+12)
=12÷17
答:瓶中水的体积占瓶子容积的。
故答案为:。
13.(2024春 泗水县期末)如图中,挖去中间的圆柱后,剩下部分的体积是多少立方厘米?(单位:厘米)
【解答】解:20×20×30﹣3.14×(20÷2)2×30
=12000﹣9420
=2580(立方厘米)
答:剩下部分的体积是2580立方厘米。
14.(2024 思明区)北京冬奥会U型场地设在张家口赛区,其场地如一个横着的半圆柱(如图所示),全长160米,雪槽深度6米。
(1)要建一个这样的滑雪U型池,需要挖出多少立方米的泥土?
(2)施工人员想在滑雪U型池的底部铺上旱冰,需要铺多少平方米的旱冰?
【解答】解:(1)3.14×62×160÷2
=3.14×36×160÷2
=113.04×160÷2
=18086.4÷2
=9043.2(立方米)
答:需要挖出9043.2分米泥土。
(2)2×3.14×6×160÷2
=37.68×160÷2
=6028.8÷2
=3014.4(平方米)
答:需要铺旱冰的面积是3014.4平方米。
15.(2024 秦都区)如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所示.请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 14 cm,匀速注水的水流速度为 5 cm3/s;
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
【解答】解:(1)根据水面高度h(cm)与注水时间t(s)之间的关系,
可得圆柱形容器的高为14cm,
30×(14﹣11)÷(42﹣24)
=30×3÷18
=90÷18
=5(cm3/s)
所以匀速注水的水流速度为5cm3/s.
答:圆柱形容器的高为14cm,匀速注水的水流速度为5cm3/s.
(2)“几何体”上方圆柱的高为:
11﹣(5×18)÷(30﹣15)
=11﹣90÷15
=11﹣6
=5(cm)
设“几何体”上方圆柱的底面积为scm2,
则5 (30﹣s)=5×(24﹣18),
150﹣5s=30
150﹣5s+5s=30+5s
30+5s=150
30+5s﹣30=150﹣30
5s=120
5s÷5=120÷5
s=24
所以“几何体”上方圆柱的底面积为24cm2.
答:“几何体”上方圆柱的高为5cm,底面积为24cm2.
故答案为:14,5.
16.(2024春 高新区期末)如图,沙漏是由两个完全相同的圆锥形容器组成的,单个圆锥形容器的底面直径是8cm,高为9cm。
给上面的圆锥形容器装满细沙,如果每分钟向下漏2.5cm3,那么这些沙子全部漏完大约需要多少分钟?(结果保留整数)
【解答】解:3.14×(8÷2)2×92.5
=3.14×16×92.5
=452.162.5
≈60(分钟)
答:这些沙子全部漏完大约需要60分钟。
17.(2024春 高新区期末)一个圆柱形容器,从里面量,高12厘米,底面半径10厘米,水深3厘米。把一个棱长8厘米的正方体铁块放入水中,正方体的一个面与圆柱的底面贴合,这时水深多少厘米?(结果保留一位小数)
【解答】解:8×8×3÷(3.14×102﹣8×8)+3
=64×3÷(3.14×100﹣64)+3
=192÷(314﹣64)+3
=192÷250+3
≈0.8+3
=3.8(厘米)
答:这时水深约3.8厘米。
18.(2024 綦江区)长10厘米,直径2厘米的三根圆柱捆成一捆(如图),用一张纸将这捆圆柱侧面包起来(纸要绷紧),至少需要多大面积的纸?
【解答】解:(2×3+3.14×2)×10,
=(6+6.28)×10,
=12.28×10,
=122.8(平方厘米);
答:至少需要122.8平方厘米的纸.
19.(2024 历城区)一个圆柱形木块按图甲的方式切成形状、大小相同的四块,表面积增加了600cm2;按图乙的方式切成形状、大小相同的三块,表面积增加了314cm2。求这根木料的体积。
【解答】解:600÷4=150(cm2)
即圆柱底面直径和高的乘积为150cm2。
314÷4=78.5(cm2)
78.5÷3.14=25(cm2)
25=5×5,即圆柱底面半径是5cm。
5×2=10(cm),即圆柱底面直径是10cm。
150÷10=15(cm),即圆柱高是15cm。
3.14×25×15=1177.5(cm3)
答:这根木料的体积是1177.5cm3。
20.(2024 临朐县)做实验想问题。
步骤1:准备一个底面积是10平方厘米的圆柱形空水杯。
步骤2:放入一个底面积是8平方厘米、高是6厘米的圆锥形铁块。
步骤3:向水杯里倒水,水面没过铁块即可。(不倒满)
步骤4:取出铁块,水面下降。
你能算出水面下降了多少厘米吗?
【解答】解:8×610
=16÷10
=1.6(厘米)
答:水面下降了1.6厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
