期末应用题易错精选题:圆柱和圆锥(含答案)-2024-2025学年数学六年级下册北师大版
文档属性
| 名称 | 期末应用题易错精选题:圆柱和圆锥(含答案)-2024-2025学年数学六年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 05:20:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册北师大版
1.(2024春 莱芜区期末)少先队队鼓是圆柱形的,底面直径6分米,高2分米,侧面由铝皮围成,上、下底面蒙的是羊皮。
(1)每个队鼓的体积是多少立方分米?
(2)做10个这样的队鼓,至少需要铝皮多少平方分米?
2.(2024春 平川区校级期中)一张长方形铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
3.(2024春 巨野县期中)请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择。
(1)你选择的材料是 号和 号。
(2)计算出这个水桶的铁皮面积。
4.(2024春 榕城区期中)一个装有水的圆柱形玻璃杯,从里面量得它的直径是20厘米,杯中水面距杯口3厘米。如果把一个高12厘米的圆锥形铅锤完全浸没在水中,水会溢出20毫升。这个铅锤的底面积是多少平方厘米?
5.(2024 临高县)一个圆锥形容器,底面半径是4厘米,高9厘米,将它装满水后,倒入底面积是12.56平方厘米的圆柱形容器中,水的高度是多少?
6.(2024春 金川区校级期中)如图,一个圆柱高8厘米,截下2厘米长的一段后,圆柱的表面积减少25.12平方厘米,原来圆柱的表面积是多少平方厘米?
7.(2024春 金川区校级期中)把一根高为6分米的圆柱形木料,沿直径对半切成两个半圆柱,表面积增加了120平方分米,这根木料的表面积和体积是多少?
8.(2024春 临漳县期中)如图,一个圆锥形容器里面装满水,若把这些水全部倒入长方体容器内,水面高3cm,求圆锥形容器的底面积。
9.(2024 青白江区)一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,前轮转动一周,压路的面积是多少平方米?(得数保留整数)
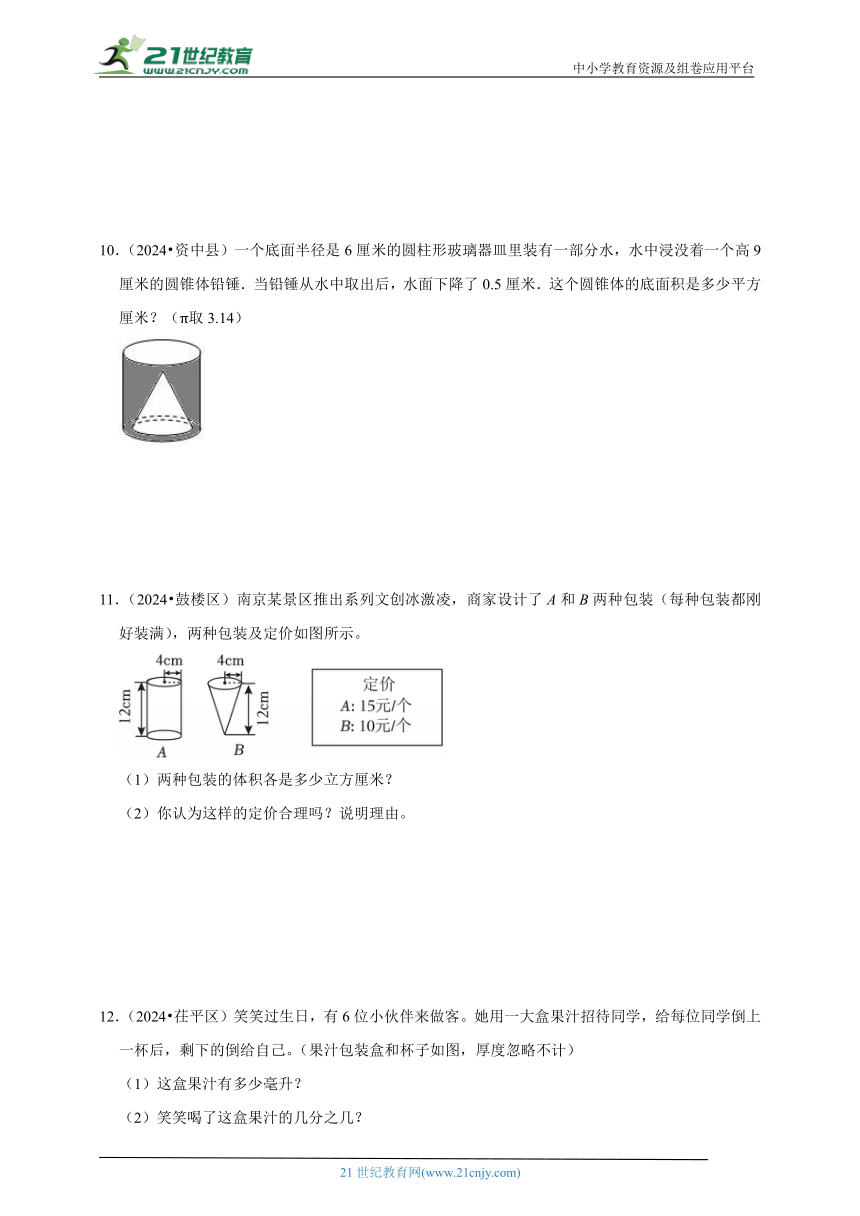
10.(2024 资中县)一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?(π取3.14)
11.(2024 鼓楼区)南京某景区推出系列文创冰激凌,商家设计了A和B两种包装(每种包装都刚好装满),两种包装及定价如图所示。
(1)两种包装的体积各是多少立方厘米?
(2)你认为这样的定价合理吗?说明理由。
12.(2024 茌平区)笑笑过生日,有6位小伙伴来做客。她用一大盒果汁招待同学,给每位同学倒上一杯后,剩下的倒给自己。(果汁包装盒和杯子如图,厚度忽略不计)
(1)这盒果汁有多少毫升?
(2)笑笑喝了这盒果汁的几分之几?
13.(2024 高新区)把底面直径10厘米、高20厘米的圆柱切成若干等份,拼成一个近似的长方体。
(1)计算这个长方体的体积。
(2)这个长方体的表面积比圆柱的表面积增加多少?
14.(2024 惠州)一底面半径为8cm的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9cm(如图)。这个圆柱形铁块的体积是多少?
15.(2024 隆昌市)把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了 48cm2;平行于底面切成三块(如图②),表面积增加了50.24cm2;削成一个最大的圆锥(如图 ③),体积减少了多少立方厘米?
16.(2024 渝中区)水平桌面上放着高度同为40厘米的两个圆柱形容器,在它们高度的一半处有一连通管相连(连通管容积忽略不计),容器A和B底面直径分别为32厘米和24厘米。先关闭连通管,将容器A注满,再打开连通管,容器B中水的高度最终是多少厘米?(π取3.14)
17.(2024 蓝山县)如图,圆柱形容器底面积和杯口的面积都是60平方厘米,圆柱形容器的高是12厘米,杯子的高是9厘米,小强将圆柱形容器里的饮料倒入该杯中,可以倒满几杯?
18.(2024 怀来县)有一种圆柱形饮料罐,底面直径是6厘米,高是10厘米。将12罐这种饮料放入一个长方体纸箱(如图所示)。求纸箱的容积是多少立方厘米?
19.(2024 南宁)一个直角三角形ABC(如图所示),以直角边AB为轴旋转一周,得到一个圆锥,这个圆锥的体积是多少?
20.(2024 平昌县)如图所示是一个由圆柱和圆锥组成的容器,圆柱的高是10厘米,圆锥的高是6厘米,如图左放置时,容器里的水深6厘米,将这个容器倒过来如右图放置时,圆锥的顶点到水面的距离是多少厘米?请先算一算,并在右图中画出水深情况。(单位:厘米)
21.(2024 太和县)有一长方形ABCD(如图),长是6cm,宽是4cm,以AD边所在的直线为轴旋转一周。其中涂色部分所形成的旋转体的体积是多少立方分米?
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册北师大版
参考答案与试题解析
一.解答题(共21小题)
1.(2024春 莱芜区期末)少先队队鼓是圆柱形的,底面直径6分米,高2分米,侧面由铝皮围成,上、下底面蒙的是羊皮。
(1)每个队鼓的体积是多少立方分米?
(2)做10个这样的队鼓,至少需要铝皮多少平方分米?
【解答】解:(1)3.14×(6÷2)2×2
=3.14×18
=56.52(立方分米)
答:每个队鼓的体积是56.52立方分米。
(2)3.14×6×2×10
=18.84×20
=376.8(平方分米)
答:做10个这样的队鼓,至少需要铝皮376.8平方分米。
2.(2024春 平川区校级期中)一张长方形铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
【解答】解:3.14×102×2
=3.14×100×2
=314×2
=628(平方厘米)
3.14×2×10×(10×2)
=6.28×10×20
=62.8×20
=1256(平方厘米)
628+1256=1884(平方厘米)
答:圆柱体铁皮的表面积是1884平方厘米。
3.(2024春 巨野县期中)请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择。
(1)你选择的材料是 ① 号和 ④ 号。
(2)计算出这个水桶的铁皮面积。
【解答】解:(1)①中的长方形长为12.56dm,只有④中的圆周长为:2×3.14×2=12.56(dm),则选择的材料是①和④(答案不唯一)。
(2)水桶的铁皮面积为:
12.56×2+3.14×22
=12.56×2+3.14×4
=25.12+12.56
=37.68(dm2)
答:这个水桶的铁皮面积是37.68 dm2。
4.(2024春 榕城区期中)一个装有水的圆柱形玻璃杯,从里面量得它的直径是20厘米,杯中水面距杯口3厘米。如果把一个高12厘米的圆锥形铅锤完全浸没在水中,水会溢出20毫升。这个铅锤的底面积是多少平方厘米?
【解答】解:20毫升=20立方厘米
[3.14×(20÷2)2×3+20]×3÷12
=[3.14×100×3+20]×3÷12
=[942+20]×3÷12
=962×3÷12
=2886÷12
=240.5(平方厘米)
答:这个铅锤的底面积是240.5平方厘米。
5.(2024 临高县)一个圆锥形容器,底面半径是4厘米,高9厘米,将它装满水后,倒入底面积是12.56平方厘米的圆柱形容器中,水的高度是多少?
【解答】解:圆锥形容器里水的体积:
3.14×42×9
3.14×16×9
=3.14×16×3
=50.24×3
=150.72(立方厘米)
水的高度:150.72÷12.56=12(厘米)
答:水的高度是12厘米.
6.(2024春 金川区校级期中)如图,一个圆柱高8厘米,截下2厘米长的一段后,圆柱的表面积减少25.12平方厘米,原来圆柱的表面积是多少平方厘米?
【解答】解:底面周长:25.12÷2=12.56(厘米)
底面半径:12.56÷3.14÷2=2(厘米)
两个底面积:
3.14×22×2
=3.14×8
=25.12(平方厘米)
侧面积:12.56×8=100.48(平方厘米)
表面积:100.48+25.12=125.6(平方厘米)
答:原来圆柱的表面积是125.6平方厘米.
7.(2024春 金川区校级期中)把一根高为6分米的圆柱形木料,沿直径对半切成两个半圆柱,表面积增加了120平方分米,这根木料的表面积和体积是多少?
【解答】解:120÷2=60(平方分米)
60÷6=10(分米)
10÷2=5(分米)
S表=2πr2+2πrh
=2×3.14×52+2×3.14×5×6
=157+188.4
=345.4(dm2)
V=πr2h
=3.14×52×10
=785(dm3)
答:这根木料的表面积是345.4dm2,体积是785dm3。
8.(2024春 临漳县期中)如图,一个圆锥形容器里面装满水,若把这些水全部倒入长方体容器内,水面高3cm,求圆锥形容器的底面积。
【解答】解:(5×5×3)÷10
=(25×3)÷10
=75÷10
=7.5
=22.5(平方厘米)
答:圆锥形容器的底面积是22.5平方厘米。
9.(2024 青白江区)一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,前轮转动一周,压路的面积是多少平方米?(得数保留整数)
【解答】解:3.14×0.8×1.6
=3.14×1.28
≈4(平方米)
答:前轮滚动一周,压路的面积约是4平方米.
10.(2024 资中县)一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?(π取3.14)
【解答】解:容器水下降的体积:
3.14×62×0.5
=3.14×36×0.5
=56.52(立方厘米);
圆锥的底面积:
56.52÷(9)
=56.52÷3
=18.84(平方厘米);
答:这个圆锥体的底面积是18.84平方厘米.
11.(2024 鼓楼区)南京某景区推出系列文创冰激凌,商家设计了A和B两种包装(每种包装都刚好装满),两种包装及定价如图所示。
(1)两种包装的体积各是多少立方厘米?
(2)你认为这样的定价合理吗?说明理由。
【解答】解:(1)4×4×3.14×12
=16×3.14×12
=602.88(立方厘米)
(立方厘米)
答:A包装的体积是602.88立方厘米,B包装的体积是200.96立方厘米。
(2)体积比是:B:A=200.96:602.88=1:
单价比是:
因为,所以这样的定价不合理。(理由合理即可)
12.(2024 茌平区)笑笑过生日,有6位小伙伴来做客。她用一大盒果汁招待同学,给每位同学倒上一杯后,剩下的倒给自己。(果汁包装盒和杯子如图,厚度忽略不计)
(1)这盒果汁有多少毫升?
(2)笑笑喝了这盒果汁的几分之几?
【解答】解:(1)12×6×15
=72×15
=1080(立方厘米)
1080立方厘米=1080毫升
答:这盒果汁有1080毫升。
(2)20×8=160(立方厘米)
160立方厘米=160毫升
(1080﹣160×6)÷1080
=(1080﹣960)÷1080
=120÷1080
答:笑笑喝了这盒果汁的。
13.(2024 高新区)把底面直径10厘米、高20厘米的圆柱切成若干等份,拼成一个近似的长方体。
(1)计算这个长方体的体积。
(2)这个长方体的表面积比圆柱的表面积增加多少?
【解答】解:(1)314×(10÷2)2×20
=3.14×25×20
=1570 (立方厘米)
答:个长方体的体积是1570立方厘米。
(2)(10÷2)×20×2
=5×20×2
=200(平方厘米)
答:这个长方体的表面积比圆柱的表面积增加了200平方厘米。
14.(2024 惠州)一底面半径为8cm的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9cm(如图)。这个圆柱形铁块的体积是多少?
【解答】解:3.14×82×(9﹣5)÷(3+1)×3
=3.14×64×4÷4×3
=200.96×4÷4×3
=200.96×3
=602.88(立方厘米)
答:圆柱形铁块的体积是602.88立方厘米。
15.(2024 隆昌市)把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了 48cm2;平行于底面切成三块(如图②),表面积增加了50.24cm2;削成一个最大的圆锥(如图 ③),体积减少了多少立方厘米?
【解答】解:设圆柱的半径为rcm,高为hcm。
由图①得,rh×8=48,即rh=48÷8=6(cm2)
由图②得,πr2×4=50.24,r2=50.24÷4÷3.14=4,所以r=2(cm)
h=6÷2=3(cm)
减少的体积:
3.14×22×33.14×22×3
3.14×4×3
=3.14×8
=25.12(cm3)
答:体积减小了25.12cm3。
16.(2024 渝中区)水平桌面上放着高度同为40厘米的两个圆柱形容器,在它们高度的一半处有一连通管相连(连通管容积忽略不计),容器A和B底面直径分别为32厘米和24厘米。先关闭连通管,将容器A注满,再打开连通管,容器B中水的高度最终是多少厘米?(π取3.14)
【解答】解:π×(32÷2)2×40
=π×162×40
=π×256×40
=10240π(立方厘米)
π×(32÷2)2:π×(24÷2)2
=162:122
=256:144
=16:9
(立方厘米)
3686.4π÷[π×(24÷2)2]
=3686.4π÷[π×122]
=3686.4π÷144π
=25.6(厘米)
答:容器B中水的高度最终是25.6厘米。
17.(2024 蓝山县)如图,圆柱形容器底面积和杯口的面积都是60平方厘米,圆柱形容器的高是12厘米,杯子的高是9厘米,小强将圆柱形容器里的饮料倒入该杯中,可以倒满几杯?
【解答】解:60×12÷(60×9)
=720÷180
=4(杯)
答:可以倒满4杯。
18.(2024 怀来县)有一种圆柱形饮料罐,底面直径是6厘米,高是10厘米。将12罐这种饮料放入一个长方体纸箱(如图所示)。求纸箱的容积是多少立方厘米?
【解答】解:(4×6)×(3×6)×10
=24×18×10
=432×10
=4320(立方厘米)
答:纸箱的容积是4230立方厘米。
19.(2024 南宁)一个直角三角形ABC(如图所示),以直角边AB为轴旋转一周,得到一个圆锥,这个圆锥的体积是多少?
【解答】解:3.14×32×4
=3.14×3×4
=37.68(立方厘米)
答:这个圆锥的体积是37.68立方厘米。
20.(2024 平昌县)如图所示是一个由圆柱和圆锥组成的容器,圆柱的高是10厘米,圆锥的高是6厘米,如图左放置时,容器里的水深6厘米,将这个容器倒过来如右图放置时,圆锥的顶点到水面的距离是多少厘米?请先算一算,并在右图中画出水深情况。(单位:厘米)
【解答】解:6﹣6÷3+6
=6﹣2+6
=4+6
=10(厘米)
答:从圆锥的顶点到液面的高是10厘米。
21.(2024 太和县)有一长方形ABCD(如图),长是6cm,宽是4cm,以AD边所在的直线为轴旋转一周。其中涂色部分所形成的旋转体的体积是多少立方分米?
【解答】解:3.14×4×4×6﹣3.14×4×4×6÷3
=301.44﹣301.44÷3
=200.96(立方厘米)
200.96立方厘米=0.20096立方分米
答:其中涂色部分所形成的旋转体的体积是0.20096立方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册北师大版
1.(2024春 莱芜区期末)少先队队鼓是圆柱形的,底面直径6分米,高2分米,侧面由铝皮围成,上、下底面蒙的是羊皮。
(1)每个队鼓的体积是多少立方分米?
(2)做10个这样的队鼓,至少需要铝皮多少平方分米?
2.(2024春 平川区校级期中)一张长方形铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
3.(2024春 巨野县期中)请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择。
(1)你选择的材料是 号和 号。
(2)计算出这个水桶的铁皮面积。
4.(2024春 榕城区期中)一个装有水的圆柱形玻璃杯,从里面量得它的直径是20厘米,杯中水面距杯口3厘米。如果把一个高12厘米的圆锥形铅锤完全浸没在水中,水会溢出20毫升。这个铅锤的底面积是多少平方厘米?
5.(2024 临高县)一个圆锥形容器,底面半径是4厘米,高9厘米,将它装满水后,倒入底面积是12.56平方厘米的圆柱形容器中,水的高度是多少?
6.(2024春 金川区校级期中)如图,一个圆柱高8厘米,截下2厘米长的一段后,圆柱的表面积减少25.12平方厘米,原来圆柱的表面积是多少平方厘米?
7.(2024春 金川区校级期中)把一根高为6分米的圆柱形木料,沿直径对半切成两个半圆柱,表面积增加了120平方分米,这根木料的表面积和体积是多少?
8.(2024春 临漳县期中)如图,一个圆锥形容器里面装满水,若把这些水全部倒入长方体容器内,水面高3cm,求圆锥形容器的底面积。
9.(2024 青白江区)一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,前轮转动一周,压路的面积是多少平方米?(得数保留整数)
10.(2024 资中县)一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?(π取3.14)
11.(2024 鼓楼区)南京某景区推出系列文创冰激凌,商家设计了A和B两种包装(每种包装都刚好装满),两种包装及定价如图所示。
(1)两种包装的体积各是多少立方厘米?
(2)你认为这样的定价合理吗?说明理由。
12.(2024 茌平区)笑笑过生日,有6位小伙伴来做客。她用一大盒果汁招待同学,给每位同学倒上一杯后,剩下的倒给自己。(果汁包装盒和杯子如图,厚度忽略不计)
(1)这盒果汁有多少毫升?
(2)笑笑喝了这盒果汁的几分之几?
13.(2024 高新区)把底面直径10厘米、高20厘米的圆柱切成若干等份,拼成一个近似的长方体。
(1)计算这个长方体的体积。
(2)这个长方体的表面积比圆柱的表面积增加多少?
14.(2024 惠州)一底面半径为8cm的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9cm(如图)。这个圆柱形铁块的体积是多少?
15.(2024 隆昌市)把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了 48cm2;平行于底面切成三块(如图②),表面积增加了50.24cm2;削成一个最大的圆锥(如图 ③),体积减少了多少立方厘米?
16.(2024 渝中区)水平桌面上放着高度同为40厘米的两个圆柱形容器,在它们高度的一半处有一连通管相连(连通管容积忽略不计),容器A和B底面直径分别为32厘米和24厘米。先关闭连通管,将容器A注满,再打开连通管,容器B中水的高度最终是多少厘米?(π取3.14)
17.(2024 蓝山县)如图,圆柱形容器底面积和杯口的面积都是60平方厘米,圆柱形容器的高是12厘米,杯子的高是9厘米,小强将圆柱形容器里的饮料倒入该杯中,可以倒满几杯?
18.(2024 怀来县)有一种圆柱形饮料罐,底面直径是6厘米,高是10厘米。将12罐这种饮料放入一个长方体纸箱(如图所示)。求纸箱的容积是多少立方厘米?
19.(2024 南宁)一个直角三角形ABC(如图所示),以直角边AB为轴旋转一周,得到一个圆锥,这个圆锥的体积是多少?
20.(2024 平昌县)如图所示是一个由圆柱和圆锥组成的容器,圆柱的高是10厘米,圆锥的高是6厘米,如图左放置时,容器里的水深6厘米,将这个容器倒过来如右图放置时,圆锥的顶点到水面的距离是多少厘米?请先算一算,并在右图中画出水深情况。(单位:厘米)
21.(2024 太和县)有一长方形ABCD(如图),长是6cm,宽是4cm,以AD边所在的直线为轴旋转一周。其中涂色部分所形成的旋转体的体积是多少立方分米?
期末应用题易错精选题:圆柱和圆锥-2024-2025学年数学六年级下册北师大版
参考答案与试题解析
一.解答题(共21小题)
1.(2024春 莱芜区期末)少先队队鼓是圆柱形的,底面直径6分米,高2分米,侧面由铝皮围成,上、下底面蒙的是羊皮。
(1)每个队鼓的体积是多少立方分米?
(2)做10个这样的队鼓,至少需要铝皮多少平方分米?
【解答】解:(1)3.14×(6÷2)2×2
=3.14×18
=56.52(立方分米)
答:每个队鼓的体积是56.52立方分米。
(2)3.14×6×2×10
=18.84×20
=376.8(平方分米)
答:做10个这样的队鼓,至少需要铝皮376.8平方分米。
2.(2024春 平川区校级期中)一张长方形铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个底面半径为10厘米的圆柱体,圆柱体铁皮的表面积是多少平方厘米?
【解答】解:3.14×102×2
=3.14×100×2
=314×2
=628(平方厘米)
3.14×2×10×(10×2)
=6.28×10×20
=62.8×20
=1256(平方厘米)
628+1256=1884(平方厘米)
答:圆柱体铁皮的表面积是1884平方厘米。
3.(2024春 巨野县期中)请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可搭配选择。
(1)你选择的材料是 ① 号和 ④ 号。
(2)计算出这个水桶的铁皮面积。
【解答】解:(1)①中的长方形长为12.56dm,只有④中的圆周长为:2×3.14×2=12.56(dm),则选择的材料是①和④(答案不唯一)。
(2)水桶的铁皮面积为:
12.56×2+3.14×22
=12.56×2+3.14×4
=25.12+12.56
=37.68(dm2)
答:这个水桶的铁皮面积是37.68 dm2。
4.(2024春 榕城区期中)一个装有水的圆柱形玻璃杯,从里面量得它的直径是20厘米,杯中水面距杯口3厘米。如果把一个高12厘米的圆锥形铅锤完全浸没在水中,水会溢出20毫升。这个铅锤的底面积是多少平方厘米?
【解答】解:20毫升=20立方厘米
[3.14×(20÷2)2×3+20]×3÷12
=[3.14×100×3+20]×3÷12
=[942+20]×3÷12
=962×3÷12
=2886÷12
=240.5(平方厘米)
答:这个铅锤的底面积是240.5平方厘米。
5.(2024 临高县)一个圆锥形容器,底面半径是4厘米,高9厘米,将它装满水后,倒入底面积是12.56平方厘米的圆柱形容器中,水的高度是多少?
【解答】解:圆锥形容器里水的体积:
3.14×42×9
3.14×16×9
=3.14×16×3
=50.24×3
=150.72(立方厘米)
水的高度:150.72÷12.56=12(厘米)
答:水的高度是12厘米.
6.(2024春 金川区校级期中)如图,一个圆柱高8厘米,截下2厘米长的一段后,圆柱的表面积减少25.12平方厘米,原来圆柱的表面积是多少平方厘米?
【解答】解:底面周长:25.12÷2=12.56(厘米)
底面半径:12.56÷3.14÷2=2(厘米)
两个底面积:
3.14×22×2
=3.14×8
=25.12(平方厘米)
侧面积:12.56×8=100.48(平方厘米)
表面积:100.48+25.12=125.6(平方厘米)
答:原来圆柱的表面积是125.6平方厘米.
7.(2024春 金川区校级期中)把一根高为6分米的圆柱形木料,沿直径对半切成两个半圆柱,表面积增加了120平方分米,这根木料的表面积和体积是多少?
【解答】解:120÷2=60(平方分米)
60÷6=10(分米)
10÷2=5(分米)
S表=2πr2+2πrh
=2×3.14×52+2×3.14×5×6
=157+188.4
=345.4(dm2)
V=πr2h
=3.14×52×10
=785(dm3)
答:这根木料的表面积是345.4dm2,体积是785dm3。
8.(2024春 临漳县期中)如图,一个圆锥形容器里面装满水,若把这些水全部倒入长方体容器内,水面高3cm,求圆锥形容器的底面积。
【解答】解:(5×5×3)÷10
=(25×3)÷10
=75÷10
=7.5
=22.5(平方厘米)
答:圆锥形容器的底面积是22.5平方厘米。
9.(2024 青白江区)一辆压路机的前轮是圆柱形,轮宽1.6米,直径是0.8米,前轮转动一周,压路的面积是多少平方米?(得数保留整数)
【解答】解:3.14×0.8×1.6
=3.14×1.28
≈4(平方米)
答:前轮滚动一周,压路的面积约是4平方米.
10.(2024 资中县)一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9厘米的圆锥体铅锤.当铅锤从水中取出后,水面下降了0.5厘米.这个圆锥体的底面积是多少平方厘米?(π取3.14)
【解答】解:容器水下降的体积:
3.14×62×0.5
=3.14×36×0.5
=56.52(立方厘米);
圆锥的底面积:
56.52÷(9)
=56.52÷3
=18.84(平方厘米);
答:这个圆锥体的底面积是18.84平方厘米.
11.(2024 鼓楼区)南京某景区推出系列文创冰激凌,商家设计了A和B两种包装(每种包装都刚好装满),两种包装及定价如图所示。
(1)两种包装的体积各是多少立方厘米?
(2)你认为这样的定价合理吗?说明理由。
【解答】解:(1)4×4×3.14×12
=16×3.14×12
=602.88(立方厘米)
(立方厘米)
答:A包装的体积是602.88立方厘米,B包装的体积是200.96立方厘米。
(2)体积比是:B:A=200.96:602.88=1:
单价比是:
因为,所以这样的定价不合理。(理由合理即可)
12.(2024 茌平区)笑笑过生日,有6位小伙伴来做客。她用一大盒果汁招待同学,给每位同学倒上一杯后,剩下的倒给自己。(果汁包装盒和杯子如图,厚度忽略不计)
(1)这盒果汁有多少毫升?
(2)笑笑喝了这盒果汁的几分之几?
【解答】解:(1)12×6×15
=72×15
=1080(立方厘米)
1080立方厘米=1080毫升
答:这盒果汁有1080毫升。
(2)20×8=160(立方厘米)
160立方厘米=160毫升
(1080﹣160×6)÷1080
=(1080﹣960)÷1080
=120÷1080
答:笑笑喝了这盒果汁的。
13.(2024 高新区)把底面直径10厘米、高20厘米的圆柱切成若干等份,拼成一个近似的长方体。
(1)计算这个长方体的体积。
(2)这个长方体的表面积比圆柱的表面积增加多少?
【解答】解:(1)314×(10÷2)2×20
=3.14×25×20
=1570 (立方厘米)
答:个长方体的体积是1570立方厘米。
(2)(10÷2)×20×2
=5×20×2
=200(平方厘米)
答:这个长方体的表面积比圆柱的表面积增加了200平方厘米。
14.(2024 惠州)一底面半径为8cm的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到9cm(如图)。这个圆柱形铁块的体积是多少?
【解答】解:3.14×82×(9﹣5)÷(3+1)×3
=3.14×64×4÷4×3
=200.96×4÷4×3
=200.96×3
=602.88(立方厘米)
答:圆柱形铁块的体积是602.88立方厘米。
15.(2024 隆昌市)把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了 48cm2;平行于底面切成三块(如图②),表面积增加了50.24cm2;削成一个最大的圆锥(如图 ③),体积减少了多少立方厘米?
【解答】解:设圆柱的半径为rcm,高为hcm。
由图①得,rh×8=48,即rh=48÷8=6(cm2)
由图②得,πr2×4=50.24,r2=50.24÷4÷3.14=4,所以r=2(cm)
h=6÷2=3(cm)
减少的体积:
3.14×22×33.14×22×3
3.14×4×3
=3.14×8
=25.12(cm3)
答:体积减小了25.12cm3。
16.(2024 渝中区)水平桌面上放着高度同为40厘米的两个圆柱形容器,在它们高度的一半处有一连通管相连(连通管容积忽略不计),容器A和B底面直径分别为32厘米和24厘米。先关闭连通管,将容器A注满,再打开连通管,容器B中水的高度最终是多少厘米?(π取3.14)
【解答】解:π×(32÷2)2×40
=π×162×40
=π×256×40
=10240π(立方厘米)
π×(32÷2)2:π×(24÷2)2
=162:122
=256:144
=16:9
(立方厘米)
3686.4π÷[π×(24÷2)2]
=3686.4π÷[π×122]
=3686.4π÷144π
=25.6(厘米)
答:容器B中水的高度最终是25.6厘米。
17.(2024 蓝山县)如图,圆柱形容器底面积和杯口的面积都是60平方厘米,圆柱形容器的高是12厘米,杯子的高是9厘米,小强将圆柱形容器里的饮料倒入该杯中,可以倒满几杯?
【解答】解:60×12÷(60×9)
=720÷180
=4(杯)
答:可以倒满4杯。
18.(2024 怀来县)有一种圆柱形饮料罐,底面直径是6厘米,高是10厘米。将12罐这种饮料放入一个长方体纸箱(如图所示)。求纸箱的容积是多少立方厘米?
【解答】解:(4×6)×(3×6)×10
=24×18×10
=432×10
=4320(立方厘米)
答:纸箱的容积是4230立方厘米。
19.(2024 南宁)一个直角三角形ABC(如图所示),以直角边AB为轴旋转一周,得到一个圆锥,这个圆锥的体积是多少?
【解答】解:3.14×32×4
=3.14×3×4
=37.68(立方厘米)
答:这个圆锥的体积是37.68立方厘米。
20.(2024 平昌县)如图所示是一个由圆柱和圆锥组成的容器,圆柱的高是10厘米,圆锥的高是6厘米,如图左放置时,容器里的水深6厘米,将这个容器倒过来如右图放置时,圆锥的顶点到水面的距离是多少厘米?请先算一算,并在右图中画出水深情况。(单位:厘米)
【解答】解:6﹣6÷3+6
=6﹣2+6
=4+6
=10(厘米)
答:从圆锥的顶点到液面的高是10厘米。
21.(2024 太和县)有一长方形ABCD(如图),长是6cm,宽是4cm,以AD边所在的直线为轴旋转一周。其中涂色部分所形成的旋转体的体积是多少立方分米?
【解答】解:3.14×4×4×6﹣3.14×4×4×6÷3
=301.44﹣301.44÷3
=200.96(立方厘米)
200.96立方厘米=0.20096立方分米
答:其中涂色部分所形成的旋转体的体积是0.20096立方分米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
