公式法(一)
图片预览




文档简介
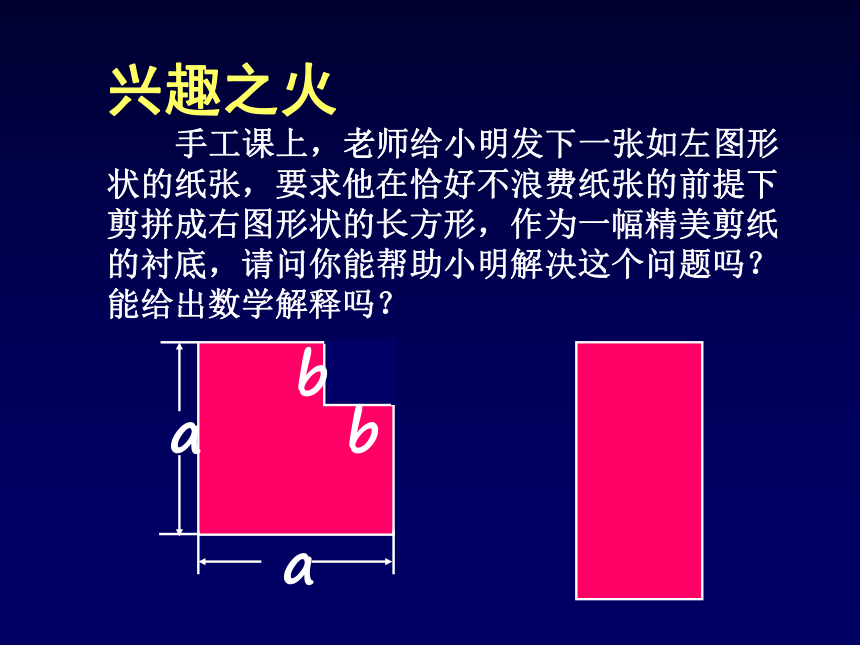
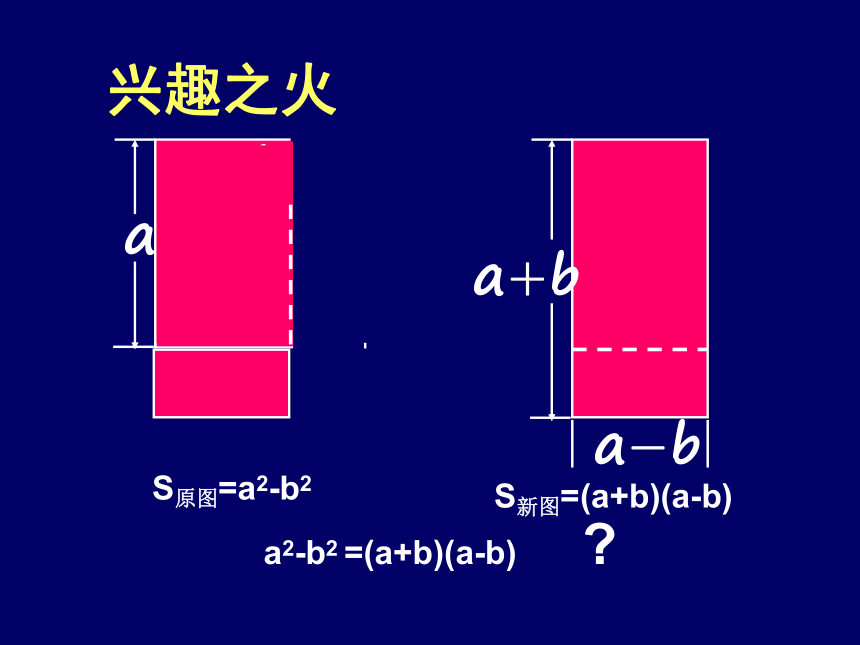
课件19张PPT。15.4.2 公式法(一)辽宁省葫芦岛市杨家杖子第二中学授课教师:田 莉 手工课上,老师给小明发下一张如左图形状的纸张,要求他在恰好不浪费纸张的前提下剪拼成右图形状的长方形,作为一幅精美剪纸的衬底,请问你能帮助小明解决这个问题吗?能给出数学解释吗?兴趣之火baabS原图=a2-b2S新图=(a+b)(a-b)a2-b2 =(a+b)(a-b) ?兴趣之火提公因式法分解因式分解因式(2)(1)3a3b2-12ab3a(x - y)2 - b(y- x)2
x2y2 - z2
兴趣之火因式分解与整式乘法有什么联系?我们学过哪些乘法公式?互逆恒等变形兴趣之火 请看乘法公式:
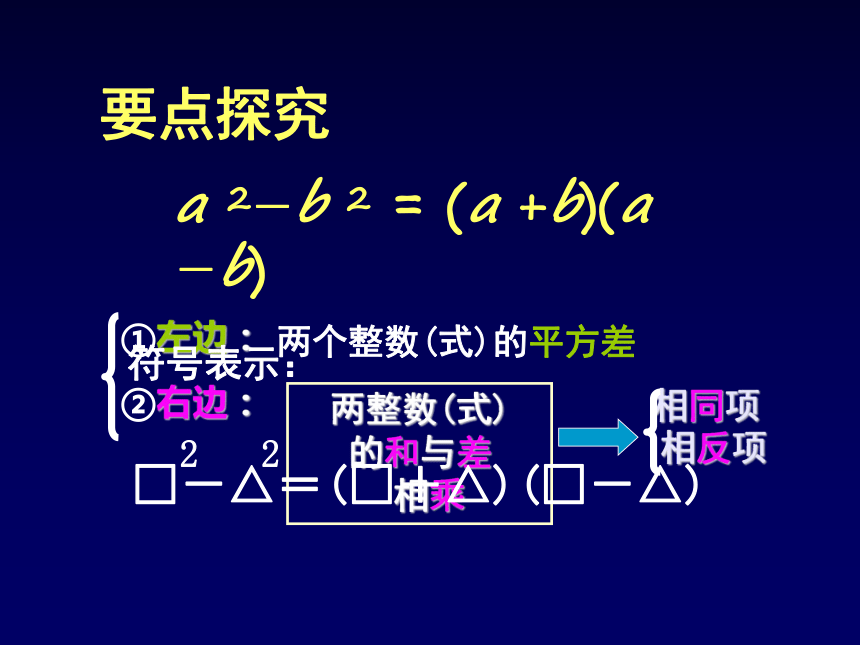
(a +b)(a -b)=a 2-b 2 左边是 ,右边是 ,把这个等式反过来就是:a 2-b 2 = (a +b)(a-b) 左边是 ,右边是 。 大家判断一下,第二个式子从左边到右边是否是因式分解?一个多项式整式的乘积整式乘法 一个多项式要点探究 两整数(式)
的和与差
相乘两个整数(式)的平方差①左边:
②右边: 相同项
相反项a 2-b 2 = (a +b)(a-b)符号表示:要点探究 在多项式 x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解因式的有( )
A 1个 B 2个 C 3个 D 4个明察秋毫 (ab)n= anbn(n是正整数)anbn= (ab)n (n是正整数)积的乘方例:a2b2 = (ab)2等于各因式乘方的积①25 x2 = (_____)2
②36a4 = (_____)2
③0.49 b2 = (_____)2
④64x2y2 = (_____)2
融会贯通例题:把下列各式分解因式:(1) 25 - 16x2解:学以致用(2) - 16x2 +81y2分析:根据加法交换律对上式变形
解: 分解因式将学以致用 (1) 2ab3-2ab将下列两个多项式分解因式(2) a3-16a提醒你:分解因式一定要分解到不能分解为止学以致用 ( x +2y )2- ( x-2y )2分析:运用整体的思想,将(x+2y)、 (x-2y)分别看作两个整体,逆用平方差公式分解因式学以致用——公式法战略小结直接式 (直接利用公式)连环式 (提公因式与利用公式并用)整体式 (利用整体的思想,直接利用
公式)思想方法 1.如图,在一块边长为 a cm 的正方形的四角,各剪去一个边长为 b cm 的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?aba 2? 4b2问题解决2.利用因式分解简便计算782-222
25×1012-992×25 (3)(1- )(1- )(1- )…(1- ) 122132421200921(2)问题解决3.若n为正整数,(2n+1)2-25能被4整除吗?说说你的理由。
4.已知x+y=7,x-y=5,求 x2-y2-2y+2x 的值.
问题解决①运用a2?b2= (a+b)(a?b)分解因式首先考虑提取公因式;
然后考虑用公式法;
直到每个因式不能再分解为止;
最终必是整式连乘。②分解因式顺序:收获总结
x2y2 - z2
兴趣之火因式分解与整式乘法有什么联系?我们学过哪些乘法公式?互逆恒等变形兴趣之火 请看乘法公式:
(a +b)(a -b)=a 2-b 2 左边是 ,右边是 ,把这个等式反过来就是:a 2-b 2 = (a +b)(a-b) 左边是 ,右边是 。 大家判断一下,第二个式子从左边到右边是否是因式分解?一个多项式整式的乘积整式乘法 一个多项式要点探究 两整数(式)
的和与差
相乘两个整数(式)的平方差①左边:
②右边: 相同项
相反项a 2-b 2 = (a +b)(a-b)符号表示:要点探究 在多项式 x2+y2, x2-y2 ,-x2+y2, -x2-y2中,能利用平方差公式分解因式的有( )
A 1个 B 2个 C 3个 D 4个明察秋毫 (ab)n= anbn(n是正整数)anbn= (ab)n (n是正整数)积的乘方例:a2b2 = (ab)2等于各因式乘方的积①25 x2 = (_____)2
②36a4 = (_____)2
③0.49 b2 = (_____)2
④64x2y2 = (_____)2
融会贯通例题:把下列各式分解因式:(1) 25 - 16x2解:学以致用(2) - 16x2 +81y2分析:根据加法交换律对上式变形
解: 分解因式将学以致用 (1) 2ab3-2ab将下列两个多项式分解因式(2) a3-16a提醒你:分解因式一定要分解到不能分解为止学以致用 ( x +2y )2- ( x-2y )2分析:运用整体的思想,将(x+2y)、 (x-2y)分别看作两个整体,逆用平方差公式分解因式学以致用——公式法战略小结直接式 (直接利用公式)连环式 (提公因式与利用公式并用)整体式 (利用整体的思想,直接利用
公式)思想方法 1.如图,在一块边长为 a cm 的正方形的四角,各剪去一个边长为 b cm 的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?aba 2? 4b2问题解决2.利用因式分解简便计算782-222
25×1012-992×25 (3)(1- )(1- )(1- )…(1- ) 122132421200921(2)问题解决3.若n为正整数,(2n+1)2-25能被4整除吗?说说你的理由。
4.已知x+y=7,x-y=5,求 x2-y2-2y+2x 的值.
问题解决①运用a2?b2= (a+b)(a?b)分解因式首先考虑提取公因式;
然后考虑用公式法;
直到每个因式不能再分解为止;
最终必是整式连乘。②分解因式顺序:收获总结
