2.3 第4课时 有理数的加减混合运算 课件 (29张PPT)2024-2025学年 鲁教版五四制(2024)六年级上册数学
文档属性
| 名称 | 2.3 第4课时 有理数的加减混合运算 课件 (29张PPT)2024-2025学年 鲁教版五四制(2024)六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:16:06 | ||
图片预览





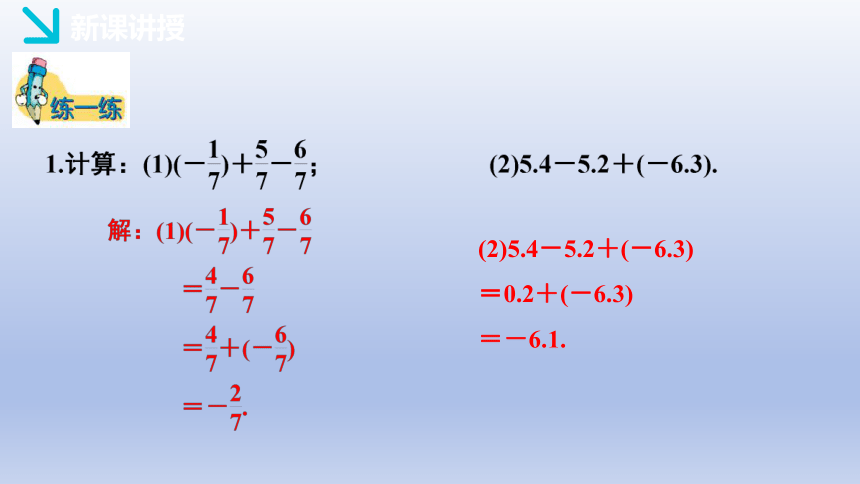

文档简介
2.3.有理数的加减运算
第二章 有理数及其运算
第4课时 有理数的加减混合运算
一辆出租车在一条东西走向的街道上营运,以出发点为初始位置,在这条街上的营运五次的结果如下表:(规定向东为正,向西为负)
情景引入
教学过程
判断出租车第五次营运后是在出发点的东边还是西边,离出发点多远?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置变化
向东2.3km
向西3.7km
向西1.8km
向东4.5km
向西4.1km
计作
+2.3
?3.7
?1.8
+4.1
?3.2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置变化
向东2.3km
向西3.7km
向西1.8km
向东4.5km
向西4.1km
计作
我们可以列出下面的算式进行计算并判断:
情景引入
教学过程
这个算式中,包含了加法运算和减法运算,这就是我们将研究的加减混合运算.
????.?????????.?????????.????+????.?????????.????
?
.
1.理解将加减混合运算统一成加法运算,掌握有理数加减混合运算的运算顺序.(重点)
重点难点
2.利用有理数的运算法则进行加减混合运算.(难点)
教学目标
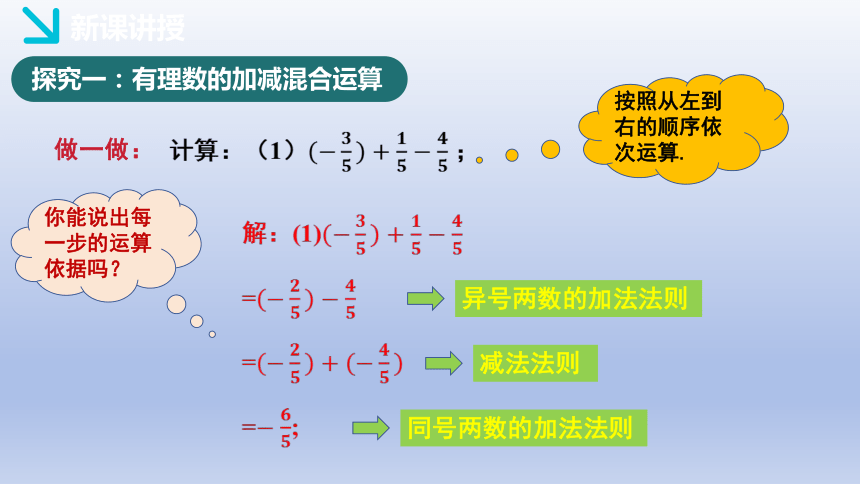
计算:(1)(?????????)+????????????????? ;
?
做一做:
新课讲授
探究一:有理数的加减混合运算
解:(1)(?????????)+?????????????????
=(?????????)?????????
=(?????????)+(?????????)
=?????????;
?
你能说出每一步的运算依据吗?
按照从左到右的顺序依次运算.
异号两数的加法法则
减法法则
同号两数的加法法则
新课讲授
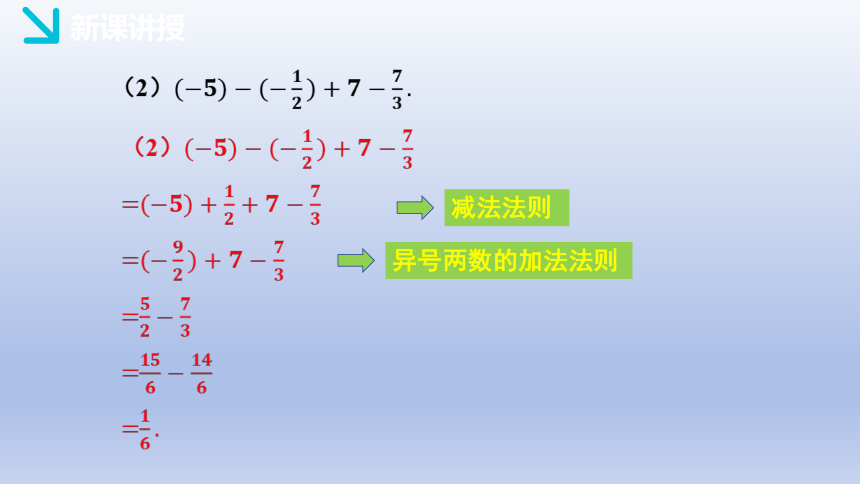
(2)(?????)?(?????????)+?????????????.
?
(2)(?????)?(?????????)+?????????????
=(?????)+????????+?????????????
=(?????????)+?????????????
=?????????????????
=?????????????????????????
=????????.
?
异号两数的加法法则
减法法则
新课讲授
有理数加减混合运算:按从左到右的顺序进行计算
知识归纳
有理数的加法和减法属于同级运算,因此,有理数的加减混合运算可以按从左到右的顺序进行.
新课讲授
(2)5.4-5.2+(-6.3)
=0.2+(-6.3)
=-6.1.
将下列式子写成省略加号和括号的和的形式.
1.(-4 )-(+7 )+( - 9 )-(-3 )
=3-4-7-9
2.( + 2.3 )-(-2.1)+(-3.2 )-4
=2.3+2.1-3.2-4
【跟踪训练】
例2 计算:
(1) ;(2)
解:原式=
解:原式=
计算:
(1)
(2)
(3)
(4)
【跟踪训练】
例3 一架飞机作特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
高度变化
上升4.5千米
下降3.2千米
上升1.1千米
下降1.4千米
记 作
+4.5千米
-3.2千米
+1.1千米
-1.4千米
加减混合运算的应用
知识点2:
解:4.5+(-3.2)+1.1+(-1.4)
=(4.5+1.1)+[(-3.2)+(-1.4)]
=5.6+(-4.6)=1(千米)
答:此时飞机比起飞点高了1千米.
例4:某汽车制造厂计划前半年内每月生产汽车20辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):
+3,-2,-1,+4,+2,-5.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
解:(1)(+4)-(-5)=9(辆).
故生产量最多的一个月比生产量最少的一个月多生产了9辆;
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
解:(2)前半年实际总产量为
[(+3)+(-2)+(-1)+(+4)+(+2)+(-5)]
=+1(辆).
所以比原计划的总产量多了1辆.
方法总结
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)写成省略加号和括号的形式;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算。
当堂小结
_____________________
有理数加减混合运算
加减混合运算可以统一为____运算
使用加法的______律与______律,可以达到简化运算的目的
交换
加法
a +b-c = a +b+(-c )
结合
课堂练习
1. 计算:(1)-11 - 9 - 7 + 6 - 8 + 10;
(2)(-17) - (-8) - (-9) - (+6) - (-14);
解:(1)原式 = (-11 - 9 - 7 - 8) + (6 + 10)
= -35 + 16 = -19;
(2)原式 = -17 + 8 + 9 - 6 + 14
= (-17 - 6) + (8 + 9 + 14)
= -23 + 31 = 8;
(3)-5.75 - (-3) + (-5) - 3.25;
(4)
(3)原式 = (-5.75 - 3.25) + (3 - 5)
= -9 - 2 = -11;
(4)原式 =
= = 。
2. 小乐某星期微信收发红包的记录如下:收到 22.9 元,发出 9.9 元,收到 8.8 元,发出 35.5 元,收到 2.7 元,发出 6.6 元,收到 0.8 元,这时她的微信钱包里钱数是增加了还是减少了?增加了或减少了多少钱?
解:记收到红包为正,发出红包为负,故小乐收发红包记录为:
+22.9、-9.9、+8.8、-35.5、+2.7、-6.6、+0.8
22.9-9.9+8.8-35.5+2.7-6.6+0.8=-16.8 。
所以她微信的钱数减少了,减少了 16.8 元。
应用一 有理数的加减法统一成加法
例1 将算式-3-(-5)+(-2)写成省略加号和括号的形式,正确的是( )
A.-3-5-2 B.-3+5-2
C.-3+5+2 D.3+5-2
B
应用二 有理数加减混合运算中运算律的应用
例2 (教材典题)计算:
(1)(-13)-15+(-23);
?
解:(1) (-13)-15+(-23)
?
=(-13)+(-15)+ (-23)
?
=(-13)+(-23)+(-15)
?
=(-1)+(-15)
=-16.
(2)(-12)-(-65)+(-8)-710.
?
解:(-12)- (-65)+(-8)-710
?
=-12+65-8-710
?
=-12-8+65-710
?
=-20+12
?
=-392.
?
变式 计算:(1)(-3.2)+12.5+(-16.8)-(-2.5);
(2)(+214)-(-10)-(-218)+(-10).
?
解:原式=(-3.2)+12.5+(-16.8)+2.5
=[(-3.2)+(-16.8)]+(12.5+2.5)
=-20+15
=-5.
解:原式=214+10+218-10=(214+218)+(10-10)=438+0=438.
?
应用三 有理数加减混合运算的实际应用
例3 下表是某年全年某加油站92号汽油价格的调整情况(正号表示比表中前一次调价上涨,负号表示比表中前一次调价下降).
时间
1月14日
3月25日
6月1日
6月30日
7月28日
9月1日
9月29日
11月9日
价格变
化(元/t)
-140
+290
+400
+600
-220
+300
-190
+480
与上一年年底相比,11月9日该加油站92号汽油价格是上涨了还是下降了?每吨变化了多少元?
解:-140+290+400+600-220+300-190+480=1520(元).
因此,与上一年年底相比,11月9日该加油站92号汽油价格上涨了,每吨上涨了1520元.
12. 已知| a |=2,- b =3, c 是最大的负整数.求:
(1) a , b , c 的值;
解:(1)因为| a |=2,- b =3, c 是最大的负整数,
所以 a =±2, b =-3, c =-1.
(2)| b - c |的值;
解:(2)因为 b =-3, c =-1,
所以| b - c |=|-3+1|=2.
解:(3)当 a =-2时,
a + b - c =-2-3-(-1)=-4;
当 a =2时, a + b - c =2-3-(-1)=0.
所以 a + b - c 的值是-4或0.
(3) a + b - c 的值.
13. (选做)设[ a ]表示不大于 a 的最大整数,例如:[2.3]=2,
?413 =-5,[5]=5.
(1)求 215 +[-3.6]-[-7]的值;
?
解:(1)原式=2+(-4)-(-7)=2-4+7=5.
解:(2)原式=2 34 - 234 -[-2.4]+ ?614 - ?614
= 114 -2+3- 254 +7
=8- 72
= 92 .
?
(2)令{ a }= a -[ a ],求 234 -[-2.4]+ ?614 的值.
第二章 有理数及其运算
第4课时 有理数的加减混合运算
一辆出租车在一条东西走向的街道上营运,以出发点为初始位置,在这条街上的营运五次的结果如下表:(规定向东为正,向西为负)
情景引入
教学过程
判断出租车第五次营运后是在出发点的东边还是西边,离出发点多远?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置变化
向东2.3km
向西3.7km
向西1.8km
向东4.5km
向西4.1km
计作
+2.3
?3.7
?1.8
+4.1
?3.2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}位置变化
向东2.3km
向西3.7km
向西1.8km
向东4.5km
向西4.1km
计作
我们可以列出下面的算式进行计算并判断:
情景引入
教学过程
这个算式中,包含了加法运算和减法运算,这就是我们将研究的加减混合运算.
????.?????????.?????????.????+????.?????????.????
?
.
1.理解将加减混合运算统一成加法运算,掌握有理数加减混合运算的运算顺序.(重点)
重点难点
2.利用有理数的运算法则进行加减混合运算.(难点)
教学目标
计算:(1)(?????????)+????????????????? ;
?
做一做:
新课讲授
探究一:有理数的加减混合运算
解:(1)(?????????)+?????????????????
=(?????????)?????????
=(?????????)+(?????????)
=?????????;
?
你能说出每一步的运算依据吗?
按照从左到右的顺序依次运算.
异号两数的加法法则
减法法则
同号两数的加法法则
新课讲授
(2)(?????)?(?????????)+?????????????.
?
(2)(?????)?(?????????)+?????????????
=(?????)+????????+?????????????
=(?????????)+?????????????
=?????????????????
=?????????????????????????
=????????.
?
异号两数的加法法则
减法法则
新课讲授
有理数加减混合运算:按从左到右的顺序进行计算
知识归纳
有理数的加法和减法属于同级运算,因此,有理数的加减混合运算可以按从左到右的顺序进行.
新课讲授
(2)5.4-5.2+(-6.3)
=0.2+(-6.3)
=-6.1.
将下列式子写成省略加号和括号的和的形式.
1.(-4 )-(+7 )+( - 9 )-(-3 )
=3-4-7-9
2.( + 2.3 )-(-2.1)+(-3.2 )-4
=2.3+2.1-3.2-4
【跟踪训练】
例2 计算:
(1) ;(2)
解:原式=
解:原式=
计算:
(1)
(2)
(3)
(4)
【跟踪训练】
例3 一架飞机作特技表演,起飞后的高度变化如下表:
此时飞机比起飞点高了多少千米?
高度变化
上升4.5千米
下降3.2千米
上升1.1千米
下降1.4千米
记 作
+4.5千米
-3.2千米
+1.1千米
-1.4千米
加减混合运算的应用
知识点2:
解:4.5+(-3.2)+1.1+(-1.4)
=(4.5+1.1)+[(-3.2)+(-1.4)]
=5.6+(-4.6)=1(千米)
答:此时飞机比起飞点高了1千米.
例4:某汽车制造厂计划前半年内每月生产汽车20辆,由于另有任务,每月上班人数有变化,1月至6月实际每月生产量和计划每月生产量相比,变化情况如下(增加为正,减少为负,单位:辆):
+3,-2,-1,+4,+2,-5.
(1)生产量最多的一个月比生产量最少的一个月多生产多少辆?
解:(1)(+4)-(-5)=9(辆).
故生产量最多的一个月比生产量最少的一个月多生产了9辆;
(2)前半年的实际总产量是多少?比计划的总产量多了还是少了?相差多少?
解:(2)前半年实际总产量为
[(+3)+(-2)+(-1)+(+4)+(+2)+(-5)]
=+1(辆).
所以比原计划的总产量多了1辆.
方法总结
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)写成省略加号和括号的形式;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算。
当堂小结
_____________________
有理数加减混合运算
加减混合运算可以统一为____运算
使用加法的______律与______律,可以达到简化运算的目的
交换
加法
a +b-c = a +b+(-c )
结合
课堂练习
1. 计算:(1)-11 - 9 - 7 + 6 - 8 + 10;
(2)(-17) - (-8) - (-9) - (+6) - (-14);
解:(1)原式 = (-11 - 9 - 7 - 8) + (6 + 10)
= -35 + 16 = -19;
(2)原式 = -17 + 8 + 9 - 6 + 14
= (-17 - 6) + (8 + 9 + 14)
= -23 + 31 = 8;
(3)-5.75 - (-3) + (-5) - 3.25;
(4)
(3)原式 = (-5.75 - 3.25) + (3 - 5)
= -9 - 2 = -11;
(4)原式 =
= = 。
2. 小乐某星期微信收发红包的记录如下:收到 22.9 元,发出 9.9 元,收到 8.8 元,发出 35.5 元,收到 2.7 元,发出 6.6 元,收到 0.8 元,这时她的微信钱包里钱数是增加了还是减少了?增加了或减少了多少钱?
解:记收到红包为正,发出红包为负,故小乐收发红包记录为:
+22.9、-9.9、+8.8、-35.5、+2.7、-6.6、+0.8
22.9-9.9+8.8-35.5+2.7-6.6+0.8=-16.8 。
所以她微信的钱数减少了,减少了 16.8 元。
应用一 有理数的加减法统一成加法
例1 将算式-3-(-5)+(-2)写成省略加号和括号的形式,正确的是( )
A.-3-5-2 B.-3+5-2
C.-3+5+2 D.3+5-2
B
应用二 有理数加减混合运算中运算律的应用
例2 (教材典题)计算:
(1)(-13)-15+(-23);
?
解:(1) (-13)-15+(-23)
?
=(-13)+(-15)+ (-23)
?
=(-13)+(-23)+(-15)
?
=(-1)+(-15)
=-16.
(2)(-12)-(-65)+(-8)-710.
?
解:(-12)- (-65)+(-8)-710
?
=-12+65-8-710
?
=-12-8+65-710
?
=-20+12
?
=-392.
?
变式 计算:(1)(-3.2)+12.5+(-16.8)-(-2.5);
(2)(+214)-(-10)-(-218)+(-10).
?
解:原式=(-3.2)+12.5+(-16.8)+2.5
=[(-3.2)+(-16.8)]+(12.5+2.5)
=-20+15
=-5.
解:原式=214+10+218-10=(214+218)+(10-10)=438+0=438.
?
应用三 有理数加减混合运算的实际应用
例3 下表是某年全年某加油站92号汽油价格的调整情况(正号表示比表中前一次调价上涨,负号表示比表中前一次调价下降).
时间
1月14日
3月25日
6月1日
6月30日
7月28日
9月1日
9月29日
11月9日
价格变
化(元/t)
-140
+290
+400
+600
-220
+300
-190
+480
与上一年年底相比,11月9日该加油站92号汽油价格是上涨了还是下降了?每吨变化了多少元?
解:-140+290+400+600-220+300-190+480=1520(元).
因此,与上一年年底相比,11月9日该加油站92号汽油价格上涨了,每吨上涨了1520元.
12. 已知| a |=2,- b =3, c 是最大的负整数.求:
(1) a , b , c 的值;
解:(1)因为| a |=2,- b =3, c 是最大的负整数,
所以 a =±2, b =-3, c =-1.
(2)| b - c |的值;
解:(2)因为 b =-3, c =-1,
所以| b - c |=|-3+1|=2.
解:(3)当 a =-2时,
a + b - c =-2-3-(-1)=-4;
当 a =2时, a + b - c =2-3-(-1)=0.
所以 a + b - c 的值是-4或0.
(3) a + b - c 的值.
13. (选做)设[ a ]表示不大于 a 的最大整数,例如:[2.3]=2,
?413 =-5,[5]=5.
(1)求 215 +[-3.6]-[-7]的值;
?
解:(1)原式=2+(-4)-(-7)=2-4+7=5.
解:(2)原式=2 34 - 234 -[-2.4]+ ?614 - ?614
= 114 -2+3- 254 +7
=8- 72
= 92 .
?
(2)令{ a }= a -[ a ],求 234 -[-2.4]+ ?614 的值.
同课章节目录
