2.3有理数的加减运算 第2课时 课件 (21张PPT)
文档属性
| 名称 | 2.3有理数的加减运算 第2课时 课件 (21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览







文档简介
第二章 有理数及其运算
2.3 有理数的加减运算
第二课时 有理数加法运算律
学习目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算
(重点、难点)
叙述有理数的加法法则:
异号两数相加,绝对值相等时和为 0;
同号两数相加,取相同的符号,并把绝对值相加;
绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
一个数同 0 相加,仍得这个数。
复习导入
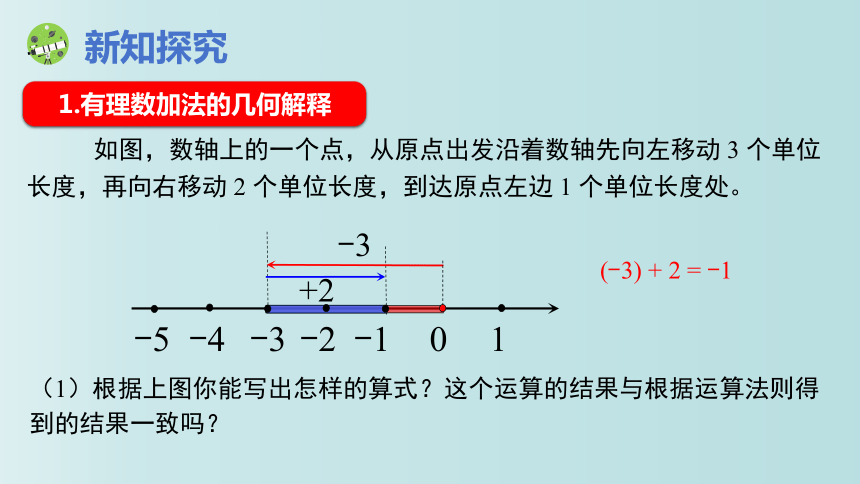
如图,数轴上的一个点,从原点出发沿着数轴先向左移动 3 个单位长度,再向右移动 2 个单位长度,到达原点左边 1 个单位长度处。
-3
0
-3
+2
-2
-1
1
-4
-5
(1)根据上图你能写出怎样的算式?这个运算的结果与根据运算法则得到的结果一致吗?
(-3) + 2 = -1
1.有理数加法的几何解释
新知探究
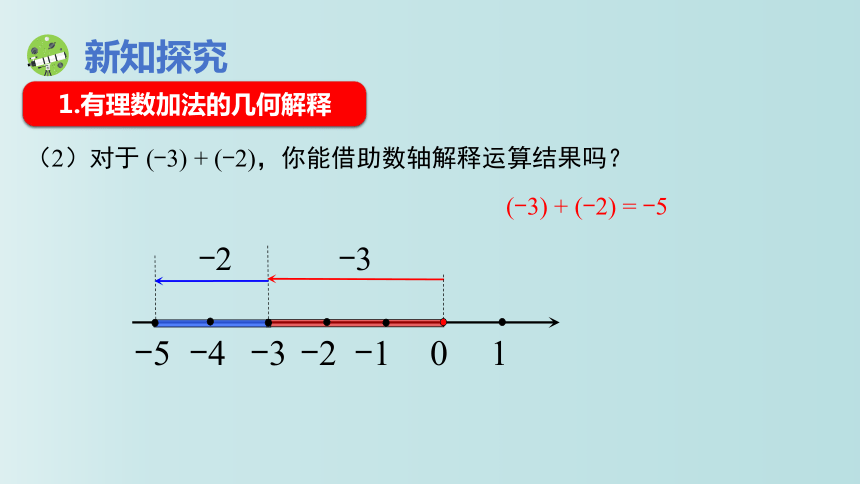
(2)对于 (-3) + (-2),你能借助数轴解释运算结果吗?
-3
0
-3
-2
-2
-1
1
-4
-5
(-3) + (-2) = -5
新知探究
1.有理数加法的几何解释
请你举一些例子试一试,并与同伴进行交流。
小学学习过哪些加法运算律?这些运算律在有理数范围内还成立吗?
事实上,加法交换律、加法结合律在有理数范围内仍然成立。
尝试——交流
概念归纳
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:a + b = b + a
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:( a + b ) + c = a + ( b + c )
5. (1)把下列各数近似地表示在数轴上;-1,-3.5,π,2.
【解】如图所示.
(2)观察(1)中的数轴,则大于-3.5小于π的所有整数的和为 .
0
大于-3.5小于π的所有整数为-3,-2,-1,0,1,2,3,
则大于-3.5小于π的所有整数的和为-3+(-2)+(-1)+0+1
+2+3=0.
例1 计算:31+(-28)+28+69
解:31+(-28)+28+69
=31+69+[(-28)+28](加法交换律和结合律)
=100+0
=100.
相反数
结合为0
计算下列各式说一说你是怎么做的。
(1)20+(-17)+15+(-10);(2)(-1.8)+(-6.5)+(-4)+6.5;
(3)(-12)+34+(-38)+66;(4)57+(-34)+(-27)+47;
?
解:=[20+(-17)]+[15+(-10)]
=3+5
=8;
=6.5+(-6.5)+(-4)+(-1.8)
=0+(-4)+(-1.8)
=-5.8;
=[(-12)+(-38)]+(34+66)
=(-50)+100
=50;
=[57+(-27)+47]+(-34)
=1+(-34)
=14。
?
简化计算常用的三个规律:
1.有相反数的可先把相反数相加,能凑整的可先凑整;
2.有分母相同的,可先把分母相同的数结合相加;
3.然后把正数或负数分别结合在一起相加.
例1 计算:
素养考点 1
运用加法运算律计算
(1)31+(-28)+28+69;
(2)(-64)+17+(-23)+68.
思考:有没有简便的方法?
(3)
(-2 ????????)+ 3 ???????? +(-3 ????????)+ 2 ???????? +(-1 ????????)+ 1 ????????
?
探究新知
探究新知
(1)解:原式=(31+69)+[(-28)+28]
(2) 解:原式=[(-64)+(-23)]+(17+68)
(加法交换律和结合律)
=100+0
=100;
(加法交换律和结合律)
=(-87)+85
(一个数同0相加,仍得这个数)
=-2.
(异号相加法则)
解:
(3)原式=
=
=
[(-2 ????????)+(-3 ????????)]+(3 ????????+2 ????????)+(-1 ????????+1 ????????)
?
-6+6+(- ????????)
?
- ????????
?
探究新知
方法点拨
使用运算律通常有下列情形:
(1)互为相反数的加数放在一起相加(相反数结合法);
(2)能凑整的加数放在一起相加(凑整法);
(3)同号的加数放在一起相加(同号结合法) ;
(4)同分母或易于通分的分数放在一起相加(同分母结合法).
探究新知
4.从一批机器零件中取出10件,称得它们的质量如下(单位:千克):206,203,199,208,207,192,202,201,197,198.请你用学过的有理数的有关知识,简便地计算出这10件零件的总质量.
解:以200千克为标准,零件质量的数据可记作:+6,+3,-1,+8,+7,-8,+2,+1,-3,-2,
则总质量为:
200×10+[6+3+(-1)+8+7+(-8)+2+1+(-3)+(-2)]
=2013(千克).
答:这10件零件的总质量为2013千克。
学以致用
【例1】计算:
31?+?(?28)?+?28?+?69
?
解:原式= 31+ 69 + [(-28)+ 28 ]
= 100 + 0
= 100
每步的依据是什么?
加法交换律和结合律
异号相加法则
同0相加法则
学以致用
【练习1】计算:
(1) 20 + (-17) + 15 + (-10);
(2) (-1.8) + (-6.5) + (-4) + 6.5;
(3) (-12) + 34 + (-38) + 66;
(4) 。
学以致用
【练习1】计算:
(1) 20 + (-17) + 15 + (-10);
解:原式 = 20 + 15 + [(-17) + (-10)]
= 35 + (-27)
= 8
符号相同
(2) (-1.8) + (-6.5) + (-4) + 6.5;
解: 原式 = [(-1.8) + (-4) ]+[(-6.5) + 6.5]
= -5.8 + 0
= -5.8
相反数
学以致用
【练习1】计算:
(3) (-12) + 34 + (-38) + 66;
解:原式 = [(-12) + (-38)] + (34 + 66)
= (-50) + 100
= 50
符号相同、
凑整十整百
同分母
(4) 。
解: 原式
学以致用
【归纳】以下情况可以考虑使用加法运算律
考虑使用加法运算律
互为相反数
符号相同
分母相同
相加得整数
先结合相加
2.3 有理数的加减运算
第二课时 有理数加法运算律
学习目标
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算
(重点、难点)
叙述有理数的加法法则:
异号两数相加,绝对值相等时和为 0;
同号两数相加,取相同的符号,并把绝对值相加;
绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
一个数同 0 相加,仍得这个数。
复习导入
如图,数轴上的一个点,从原点出发沿着数轴先向左移动 3 个单位长度,再向右移动 2 个单位长度,到达原点左边 1 个单位长度处。
-3
0
-3
+2
-2
-1
1
-4
-5
(1)根据上图你能写出怎样的算式?这个运算的结果与根据运算法则得到的结果一致吗?
(-3) + 2 = -1
1.有理数加法的几何解释
新知探究
(2)对于 (-3) + (-2),你能借助数轴解释运算结果吗?
-3
0
-3
-2
-2
-1
1
-4
-5
(-3) + (-2) = -5
新知探究
1.有理数加法的几何解释
请你举一些例子试一试,并与同伴进行交流。
小学学习过哪些加法运算律?这些运算律在有理数范围内还成立吗?
事实上,加法交换律、加法结合律在有理数范围内仍然成立。
尝试——交流
概念归纳
有理数加法中,两个数相加,交换加数的位置,和不变.
加法交换律:a + b = b + a
有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律:( a + b ) + c = a + ( b + c )
5. (1)把下列各数近似地表示在数轴上;-1,-3.5,π,2.
【解】如图所示.
(2)观察(1)中的数轴,则大于-3.5小于π的所有整数的和为 .
0
大于-3.5小于π的所有整数为-3,-2,-1,0,1,2,3,
则大于-3.5小于π的所有整数的和为-3+(-2)+(-1)+0+1
+2+3=0.
例1 计算:31+(-28)+28+69
解:31+(-28)+28+69
=31+69+[(-28)+28](加法交换律和结合律)
=100+0
=100.
相反数
结合为0
计算下列各式说一说你是怎么做的。
(1)20+(-17)+15+(-10);(2)(-1.8)+(-6.5)+(-4)+6.5;
(3)(-12)+34+(-38)+66;(4)57+(-34)+(-27)+47;
?
解:=[20+(-17)]+[15+(-10)]
=3+5
=8;
=6.5+(-6.5)+(-4)+(-1.8)
=0+(-4)+(-1.8)
=-5.8;
=[(-12)+(-38)]+(34+66)
=(-50)+100
=50;
=[57+(-27)+47]+(-34)
=1+(-34)
=14。
?
简化计算常用的三个规律:
1.有相反数的可先把相反数相加,能凑整的可先凑整;
2.有分母相同的,可先把分母相同的数结合相加;
3.然后把正数或负数分别结合在一起相加.
例1 计算:
素养考点 1
运用加法运算律计算
(1)31+(-28)+28+69;
(2)(-64)+17+(-23)+68.
思考:有没有简便的方法?
(3)
(-2 ????????)+ 3 ???????? +(-3 ????????)+ 2 ???????? +(-1 ????????)+ 1 ????????
?
探究新知
探究新知
(1)解:原式=(31+69)+[(-28)+28]
(2) 解:原式=[(-64)+(-23)]+(17+68)
(加法交换律和结合律)
=100+0
=100;
(加法交换律和结合律)
=(-87)+85
(一个数同0相加,仍得这个数)
=-2.
(异号相加法则)
解:
(3)原式=
=
=
[(-2 ????????)+(-3 ????????)]+(3 ????????+2 ????????)+(-1 ????????+1 ????????)
?
-6+6+(- ????????)
?
- ????????
?
探究新知
方法点拨
使用运算律通常有下列情形:
(1)互为相反数的加数放在一起相加(相反数结合法);
(2)能凑整的加数放在一起相加(凑整法);
(3)同号的加数放在一起相加(同号结合法) ;
(4)同分母或易于通分的分数放在一起相加(同分母结合法).
探究新知
4.从一批机器零件中取出10件,称得它们的质量如下(单位:千克):206,203,199,208,207,192,202,201,197,198.请你用学过的有理数的有关知识,简便地计算出这10件零件的总质量.
解:以200千克为标准,零件质量的数据可记作:+6,+3,-1,+8,+7,-8,+2,+1,-3,-2,
则总质量为:
200×10+[6+3+(-1)+8+7+(-8)+2+1+(-3)+(-2)]
=2013(千克).
答:这10件零件的总质量为2013千克。
学以致用
【例1】计算:
31?+?(?28)?+?28?+?69
?
解:原式= 31+ 69 + [(-28)+ 28 ]
= 100 + 0
= 100
每步的依据是什么?
加法交换律和结合律
异号相加法则
同0相加法则
学以致用
【练习1】计算:
(1) 20 + (-17) + 15 + (-10);
(2) (-1.8) + (-6.5) + (-4) + 6.5;
(3) (-12) + 34 + (-38) + 66;
(4) 。
学以致用
【练习1】计算:
(1) 20 + (-17) + 15 + (-10);
解:原式 = 20 + 15 + [(-17) + (-10)]
= 35 + (-27)
= 8
符号相同
(2) (-1.8) + (-6.5) + (-4) + 6.5;
解: 原式 = [(-1.8) + (-4) ]+[(-6.5) + 6.5]
= -5.8 + 0
= -5.8
相反数
学以致用
【练习1】计算:
(3) (-12) + 34 + (-38) + 66;
解:原式 = [(-12) + (-38)] + (34 + 66)
= (-50) + 100
= 50
符号相同、
凑整十整百
同分母
(4) 。
解: 原式
学以致用
【归纳】以下情况可以考虑使用加法运算律
考虑使用加法运算律
互为相反数
符号相同
分母相同
相加得整数
先结合相加
同课章节目录
