2.3有理数的加减运算 第2课时 课件(共22张PPT) 2024—2025学年鲁教版五四制(2024)六年级上册
文档属性
| 名称 | 2.3有理数的加减运算 第2课时 课件(共22张PPT) 2024—2025学年鲁教版五四制(2024)六年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 344.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 17:21:31 | ||
图片预览








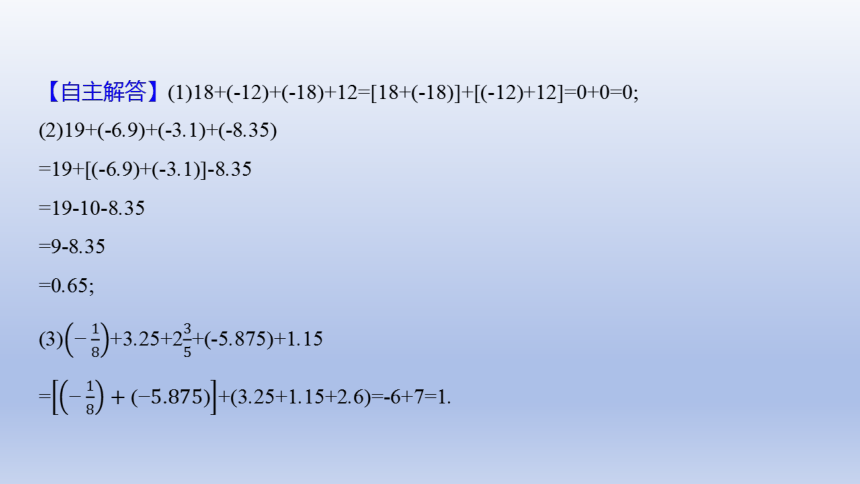
文档简介
(共22张PPT)
第二章
有理数及其运算
3 有理数的加减运算法
(第2课时)
(1)同号两数相加,取____________,_________________.
相同的符号
并把绝对值相加
(2)异号两数相加,当两数的绝对值不相等时,取
________________________, _____________________
____________________.
绝对值较大的加数的符号
减去较小的绝对值
(3)互为相反数的两个数相加得_____ .
(4)一个数与0相加,仍得 ___________.
0
这个数
并且用较大的绝对值
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算 (重点、难点)
如图,数轴上的一个点,从原点出发沿着数轴先向左移动3个单位长度,再向右移动2个单位长度,到达原点左边 单位长度处。
-5 -4 -3 -2 -1 0 1
新课导入
根据上图你能写出怎样的算式
1个
(-3)+(+2)=-1.
新课讲授
探究一:有理数加法的运算律
问题:(1)以上算式的结果与根据运算法则计算得到的结果一致吗
(-3)+(+2)
=-(3-2)
=-1.
异号两数相加
取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值
(2)对于(-3)+(-2),你能借助数轴解释运算结果吗
结果一致.
新课讲授
因此,(-3)+(-2)=-5.
-5 -4 -3 -2 -1 0 1
如图,数轴上的一个点,从原点出发沿着数轴先向左移动3个单位长度,再向左移动2个单位长度,到达原点左边5个单位长度处.
新课讲授
1 .计算:(1)(-8)+(-9) (-9)+(-8);
(2) 4 +(-7) (-7) + 4;
= -(8+9)
=-17
= -(9+8)
=-17
= -(7-4)
=-3
= -(7-4)=-3
加法交换律适用于有理数。
相等
相等
尝试·交流:小学学习过哪些加法运算律?这些运算律在有理数范围内还成立吗 请你举一些例子试一试,并与同伴进行交流。
加法交换律和加法结合律.
【典例微课】
【重点1】有理数加法的运算律的应用(运算能力)
【典例1】(教材再开发·P37例2拓展)计算:
(1)18+(-12)+(-18)+12;
(2)19+(-6.9)+(-3.1)+(-8.35);
(3)+3.25+2+(-5.875)+1.15.
【自主解答】(1)18+(-12)+(-18)+12=[18+(-18)]+[(-12)+12]=0+0=0;
(2)19+(-6.9)+(-3.1)+(-8.35)
=19+[(-6.9)+(-3.1)]-8.35
=19-10-8.35
=9-8.35
=0.65;
(3)+3.25+2+(-5.875)+1.15
=+(3.25+1.15+2.6)=-6+7=1.
【变式训练】
1.绝对值大于2且不大于5的所有整数的和是______.
【解析】根据题意,绝对值大于2且不大于5的所有整数有3,-3,4,-4,5,-5,则它们的和=3+(-3)+4+(-4)+5+(-5)=0.
0
2.用运算律计算:
(-2.8)+(-3.6)+(-1.5)+3.6.
【解析】(-2.8)+(-3.6)+(-1.5)+3.6
=[(-2.8)+(-1.5)]+[(-3.6)+3.6]
=-4.3+0
=-4.3.
【重点2】有理数加法的实际应用(运算能力、应用意识)
【典例2】(教材再开发·P44T5强化)一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的练习记录如下(单位:m):+7,-2,+10,-8,-6,+11,-12.
(1)守门员最后是否回到了球门线的位置
(2)守门员全部练习结束后,他一共跑了多少米
【自主解答】(1)(+7)+(-2)+(+10)+(-8)+(-6)+(+11)+(-12)=0(m),所以守门员最后回到了球门线的位置.
(2)|+7|+|-2|+|+10|+|-8|+|-6|+|+11|+|-12|=56(m),所以守门员练习结束后,他一共跑了56 m.
新课讲授
2 .计算:
(1) [2+(-3)]+(-8) 2+[(-3)+(-8)];
(2)[10+(-10)]+(-5) 10+[(-10)+(-5)].
= (-1)+(-8)
=-9
= 2+(-11)
=-9
= 0+(-5)
=-5
= 10+(-15)
=-5
加法结合律也适用于有理数。
相等
相等
你能用字母表示加法交换律和结合律吗?
【探究】有理数加法的运算律
【拓展提升】
探究与应用
1.运用加法运算律计算下列各题:
(1)(+66)+(-12)+(+11.3)+(-7.4)+(+8.1)+(-2.5);
(2))+(-2+(-3
=[(+66)+(+11.3)+(+8.1)]+[(-12)+(-7.4)+(-2.5)]
=85.4+(-21.9)
=63.5
=[(+3)+(+5)]+[(-2)+(-1)]+[(-3)+(+5)]
=9+(-4)+2
=5+2
=7
【探究】有理数加法的运算律
【拓展提升】
探究与应用
=[(+6)+(-6.25)]+[(+)+(+)+(-)]+(-)
=0+0+(-)
=-
【探究】有理数加法的运算律
【拓展提升】
探究与应用
2.有5筐蔬菜,以每筐50 kg为标准,超过的千克数记为正,不足的千克数记为负,称重记录如下(单位:kg):+3,-6,-4,+2,-1,总计超过或不足多少千克 5筐蔬菜的总质量是多少千克
解:与标准重量比较,5筐菜总计
3+(-6)+(-4)+2+(-1)=-6(千克);
5筐蔬菜的总重量=50×5+(-6)=244(千克).
故总计不足6千克,5筐蔬菜的总重量是244千克.
达标检测
课堂小结与检测
计算:
(1)23+(-17)+6+(-22); (2)(-8)+10+2+(-1);
(3)(-18.6)+(-6.15)+18.15+6.15;
=(23+6)+[(-17)+(-22)]
=29+(-39)
=-10
=(10+2)+[(-8)+(-1)]
=12+(-9)
=3
=[(-18.6)+18.15]+(-6.15)+6.15
=(-0.45)+0
= - 0.45
=[+(-)]+[(-)+(-)]+
=0+(-1)+
= -
2.计算:
(1)(-54)+12+(-26)+48; (2)(-6.5)+1+(-1.75)+6.
(1)-20.
(2)-0.5.
知识点2:有理数加法的应用
3.一天早晨的气温为-5 ℃,中午上升了10 ℃,半夜又下降了8 ℃,则半夜的气温是 ℃.
-3
4.在3×3方格上做填数字游戏,要求每行、每列的三个格子中的数字之和都等于0,且已填在格子中的数字如图,则a=( )
A.-21
B.11
C.21
D.39
28 a
10
8 b 13
B
5.在一次数学活动课上,数学老师将1~10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲、乙、丙、丁、戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,甲、乙、丙、丁、戊五位同学写出的结果依次是11,4,16,7,17.根据以上信息,下列判断正确的是( )
A
A.戊同学手里拿的两张卡片上的数字是8和9
B.丙同学手里拿的两张卡片上的数字是9和7
C.丁同学手里拿的两张卡片上的数字是3和4
D.甲同学手里拿的两张卡片上的数字是2和9
第二章
有理数及其运算
3 有理数的加减运算法
(第2课时)
(1)同号两数相加,取____________,_________________.
相同的符号
并把绝对值相加
(2)异号两数相加,当两数的绝对值不相等时,取
________________________, _____________________
____________________.
绝对值较大的加数的符号
减去较小的绝对值
(3)互为相反数的两个数相加得_____ .
(4)一个数与0相加,仍得 ___________.
0
这个数
并且用较大的绝对值
1.能概括出有理数的加法交换律和结合律.
2.灵活熟练地运用加法交换律、结合律简化运算 (重点、难点)
如图,数轴上的一个点,从原点出发沿着数轴先向左移动3个单位长度,再向右移动2个单位长度,到达原点左边 单位长度处。
-5 -4 -3 -2 -1 0 1
新课导入
根据上图你能写出怎样的算式
1个
(-3)+(+2)=-1.
新课讲授
探究一:有理数加法的运算律
问题:(1)以上算式的结果与根据运算法则计算得到的结果一致吗
(-3)+(+2)
=-(3-2)
=-1.
异号两数相加
取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值
(2)对于(-3)+(-2),你能借助数轴解释运算结果吗
结果一致.
新课讲授
因此,(-3)+(-2)=-5.
-5 -4 -3 -2 -1 0 1
如图,数轴上的一个点,从原点出发沿着数轴先向左移动3个单位长度,再向左移动2个单位长度,到达原点左边5个单位长度处.
新课讲授
1 .计算:(1)(-8)+(-9) (-9)+(-8);
(2) 4 +(-7) (-7) + 4;
= -(8+9)
=-17
= -(9+8)
=-17
= -(7-4)
=-3
= -(7-4)=-3
加法交换律适用于有理数。
相等
相等
尝试·交流:小学学习过哪些加法运算律?这些运算律在有理数范围内还成立吗 请你举一些例子试一试,并与同伴进行交流。
加法交换律和加法结合律.
【典例微课】
【重点1】有理数加法的运算律的应用(运算能力)
【典例1】(教材再开发·P37例2拓展)计算:
(1)18+(-12)+(-18)+12;
(2)19+(-6.9)+(-3.1)+(-8.35);
(3)+3.25+2+(-5.875)+1.15.
【自主解答】(1)18+(-12)+(-18)+12=[18+(-18)]+[(-12)+12]=0+0=0;
(2)19+(-6.9)+(-3.1)+(-8.35)
=19+[(-6.9)+(-3.1)]-8.35
=19-10-8.35
=9-8.35
=0.65;
(3)+3.25+2+(-5.875)+1.15
=+(3.25+1.15+2.6)=-6+7=1.
【变式训练】
1.绝对值大于2且不大于5的所有整数的和是______.
【解析】根据题意,绝对值大于2且不大于5的所有整数有3,-3,4,-4,5,-5,则它们的和=3+(-3)+4+(-4)+5+(-5)=0.
0
2.用运算律计算:
(-2.8)+(-3.6)+(-1.5)+3.6.
【解析】(-2.8)+(-3.6)+(-1.5)+3.6
=[(-2.8)+(-1.5)]+[(-3.6)+3.6]
=-4.3+0
=-4.3.
【重点2】有理数加法的实际应用(运算能力、应用意识)
【典例2】(教材再开发·P44T5强化)一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的练习记录如下(单位:m):+7,-2,+10,-8,-6,+11,-12.
(1)守门员最后是否回到了球门线的位置
(2)守门员全部练习结束后,他一共跑了多少米
【自主解答】(1)(+7)+(-2)+(+10)+(-8)+(-6)+(+11)+(-12)=0(m),所以守门员最后回到了球门线的位置.
(2)|+7|+|-2|+|+10|+|-8|+|-6|+|+11|+|-12|=56(m),所以守门员练习结束后,他一共跑了56 m.
新课讲授
2 .计算:
(1) [2+(-3)]+(-8) 2+[(-3)+(-8)];
(2)[10+(-10)]+(-5) 10+[(-10)+(-5)].
= (-1)+(-8)
=-9
= 2+(-11)
=-9
= 0+(-5)
=-5
= 10+(-15)
=-5
加法结合律也适用于有理数。
相等
相等
你能用字母表示加法交换律和结合律吗?
【探究】有理数加法的运算律
【拓展提升】
探究与应用
1.运用加法运算律计算下列各题:
(1)(+66)+(-12)+(+11.3)+(-7.4)+(+8.1)+(-2.5);
(2))+(-2+(-3
=[(+66)+(+11.3)+(+8.1)]+[(-12)+(-7.4)+(-2.5)]
=85.4+(-21.9)
=63.5
=[(+3)+(+5)]+[(-2)+(-1)]+[(-3)+(+5)]
=9+(-4)+2
=5+2
=7
【探究】有理数加法的运算律
【拓展提升】
探究与应用
=[(+6)+(-6.25)]+[(+)+(+)+(-)]+(-)
=0+0+(-)
=-
【探究】有理数加法的运算律
【拓展提升】
探究与应用
2.有5筐蔬菜,以每筐50 kg为标准,超过的千克数记为正,不足的千克数记为负,称重记录如下(单位:kg):+3,-6,-4,+2,-1,总计超过或不足多少千克 5筐蔬菜的总质量是多少千克
解:与标准重量比较,5筐菜总计
3+(-6)+(-4)+2+(-1)=-6(千克);
5筐蔬菜的总重量=50×5+(-6)=244(千克).
故总计不足6千克,5筐蔬菜的总重量是244千克.
达标检测
课堂小结与检测
计算:
(1)23+(-17)+6+(-22); (2)(-8)+10+2+(-1);
(3)(-18.6)+(-6.15)+18.15+6.15;
=(23+6)+[(-17)+(-22)]
=29+(-39)
=-10
=(10+2)+[(-8)+(-1)]
=12+(-9)
=3
=[(-18.6)+18.15]+(-6.15)+6.15
=(-0.45)+0
= - 0.45
=[+(-)]+[(-)+(-)]+
=0+(-1)+
= -
2.计算:
(1)(-54)+12+(-26)+48; (2)(-6.5)+1+(-1.75)+6.
(1)-20.
(2)-0.5.
知识点2:有理数加法的应用
3.一天早晨的气温为-5 ℃,中午上升了10 ℃,半夜又下降了8 ℃,则半夜的气温是 ℃.
-3
4.在3×3方格上做填数字游戏,要求每行、每列的三个格子中的数字之和都等于0,且已填在格子中的数字如图,则a=( )
A.-21
B.11
C.21
D.39
28 a
10
8 b 13
B
5.在一次数学活动课上,数学老师将1~10共十个整数依次写在十张不透明的卡片上(每张卡片上只写一个数字,每一个数字只写在一张卡片上,而且把写有数字的那一面朝下).他先像洗扑克牌一样打乱这些卡片的顺序,然后把甲、乙、丙、丁、戊五位同学叫到讲台上,随机地发给每位同学两张卡片,并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上,甲、乙、丙、丁、戊五位同学写出的结果依次是11,4,16,7,17.根据以上信息,下列判断正确的是( )
A
A.戊同学手里拿的两张卡片上的数字是8和9
B.丙同学手里拿的两张卡片上的数字是9和7
C.丁同学手里拿的两张卡片上的数字是3和4
D.甲同学手里拿的两张卡片上的数字是2和9
同课章节目录
