2.4有理数的乘除运算 第2课时 课件(30张ppt)2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4有理数的乘除运算 第2课时 课件(30张ppt)2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:27:05 | ||
图片预览










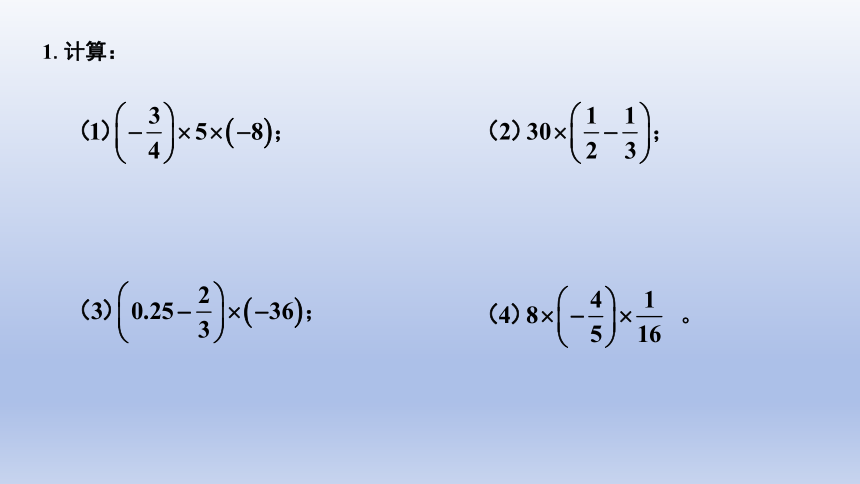
文档简介
第二章第4节
《有理数的乘法》
第二课时
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
如何进行多个有理数的乘法运算?
1、定号(奇负偶正) (2)算积的绝对值
知识回顾
你记住了吗?
问题引入
小学时候大家学过乘法的哪些运算律?
4×3=3×4
(4×3)×6=4×(3×6)
2×(3+5)=2×3+2×5
引入负数后,三种运算律是否还成立呢?
例如
乘法交换律、乘法结合律、乘法分配律
2×(-1) =
6 - 8=
(2) [2×(-3)]×(-4)=
2×[(-3)×(-4)]=
(3) 2×[3+(-4)]=
2×3+2×(-4 ) =
(1) 2×(-3) = (-2 )×3=
-6
-6
24
24
-2
-2
2× (-3) (-2) ×3
[2×(-3)]×(- 4) 2×[(-3)×(-4)]
2×[3+(-4 )] 2×3+2×(-4 )
=
=
=
(-6)×(-4) =
2×12=
结论:
乘法运算律在有理数范围内仍然适用
(探究发现,学习新知)
探究新知
有理数的乘法法则
1
例1 计算
(1) (-4)×5×(-0.25);
解:
(1) 原式=[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=+5
(2) 原式=
有没有更加简便的方法?
自主探究
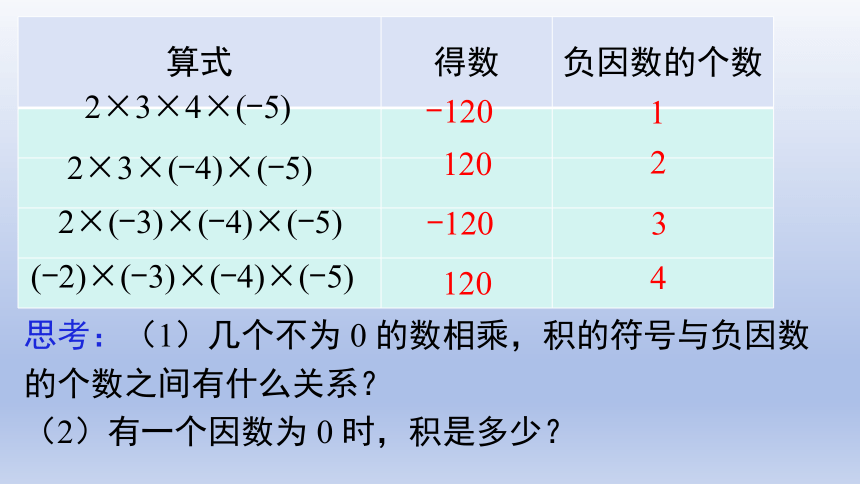
探究1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}算式
得数
负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
(2)有一个因数为 0 时,积是多少?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
有一个因数为 0 时,积是 0。
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
课堂练习
1.计算:
(1) ???????? ×(-???????????? ) ×(-????????????) ; (2) (-???????????????? )×(-???????????? ) ×0×???????? ;
?
解:
= 0
解:
(3) ???????? ×(-1.2) ×(-????????) ; (4) (-???????? )×(-???????? )×(-???????????? ) .
?
1.计算:
自主探究
例1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}算式
得数
负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
3.用乘法运算律简便计算:
(1)531×(-29)×(-2115)×(-412);
【解析】(1)????????????×(-????????)×(-2????????????)×(-4????????)
=[????????????×(-????????????????)]×[ (-????????×(-????????) ]
=-????????×1
=-????????;
?
(2) (-23)×37+(-23)×117.
【解析】(2) (-????????)×????????+(-????????)×????????????
=(-????????)×(????????+????????????)
=(-????????)×2
=-????????.
?
(10分钟·20分)
1.(3分·运算能力)下列算式中,运算结果为负数的是 ( )
A.0×(-5) B.4×(-3)×(-1)
C.(-1.5)×(-2)×(-3) D.(-2)×(-3)
2.(3分·运算能力)计算:100×(-3)×(-13)×0.01的结果是 ( )
A.1 B.-1 C.2 D.3
3.(4分·运算能力)计算:(-1)×(-9)×(-5)×(-19)=_______.?
4.(4分·运算能力·应用意识)用乘法分配律进行简便运算: (-334)×4= ____________
(只需写出接下来的一步,不必算出答案).?
?
素养当堂测评
C
A
5
?(-4+????????)×4
?
5.(6分·运算能力)运用有理数乘法运算律进行简便运算:
(1) (16-19-112)×36;
【解析】(1) (????????-????????-????????????)×36
=????????×36-????????×36-????????????×36=6-4-3=-1;
?
(2)492425×(-5).
【解析】(2)492425×(-5)
=(50-????????????)×(-5)
=-250+????????
=-?????????????????????.
?
你能看出下式的结果吗?如果能,请说明理由.
几个数相乘,如果其中有一个因数为 0,那么积等于____.
= 0
0
7.8×(-8.1)×0×(-19.6)
练一练
(2)有一个因数为 0 时,积是多少?
学以致用
5.计算:
(1)(-125)×(-2)×(-8);
(2)
(3)22×(-33)×(-4)×0.
(4)
解:(1)原式=-(125×2×8)
=-2 000.
(2)原式=?(????????????×????????????×????????)
=?????????.
?
解:(3)原式=0.
=-18.
(4)原式=?(????????×????×????????)
?
学以致用
6.计算:
学以致用
7.计算:
????????×????????×????????×????????×????????×????????×…×????????????????????????????????×????????????????????????????????×????????????????????????????????×????????????????????????????????
?
解:原式=????????×????????×????????×????????×????????×…×????????????????????????????????×????????????????????????????????×????????????????????????????????
=????????×1×1×…×1×????????????????????????????????
=????????????????????????????????
?
课堂小结
有理数的乘除运算2
多个有理数相乘的法则
有理数乘法的运算律
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.几个数相乘,有一个因数为0,则积为0.
乘法的交换律
乘法的结合律
乘法对加法的分配律
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
(既可以正用,也可以逆用)
探究一 多个有理数相乘的积的符号
[尝试交流]
计算:(1)(-4)×5×(-0.25);
解:(-4)×5×(-0.25)
=[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=5.
(2)(-35)×(-56)×(-2).
?
解:(-35)×(-56)×(-2)
?
=[+(35×56) ]×(-2)
?
=12×(-2)
?
=-(12×2)
?
=-1.
[思考交流]
几个有理数相乘,因数都不为0时,积的符号怎样确定?有一个因数为0时,积是多少?
解:几个不等于0的有理数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
几个数相乘,有一个因数为0,则积为0.
学 技巧
多个有理数相乘时积的符号确定
(1)几个不等于0的有理数相乘,积的符号由负因数的个数决
定,当负因数有奇数个时,积的符号为 ;当负因数有
偶数个时,积的符号为 .?
(2)几个数相乘,有一个因数为0,则积为 .?
负
正
0
变式2 计算:
(1)(-5)×(-145)×0.2×(-59);
(2)(-3.5+112-1)×(-10).
?
解:(1)原式=[(-5)×0.2]×[ (-95)×(-59)]=-1×1=-1.
?
(2)原式=(-3.5)×(-10)+32×(-10)-1×(-10)=35+(-15)-(-10)=
20+10=30.
?
【延伸拓展】
乘法对加法的分配律的逆应用
(1)将乘法对加法的分配律a(b+c)=ab+ac等号左右两边交换位置,得到ab+ac= .?
a(b+c)
(2)计算:
①6.868×(-17)+17×6.868;
②713×(-9)+713×(-18)+713.
?
解:①原式=6.868×(-17+17)=6.868×0=0.
②原式=713×[(-9)+(-18)+1]=713×(-26)=-14.
《有理数的乘法》
第二课时
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值
相乘任何数同0相乘,都得0.
如何进行多个有理数的乘法运算?
1、定号(奇负偶正) (2)算积的绝对值
知识回顾
你记住了吗?
问题引入
小学时候大家学过乘法的哪些运算律?
4×3=3×4
(4×3)×6=4×(3×6)
2×(3+5)=2×3+2×5
引入负数后,三种运算律是否还成立呢?
例如
乘法交换律、乘法结合律、乘法分配律
2×(-1) =
6 - 8=
(2) [2×(-3)]×(-4)=
2×[(-3)×(-4)]=
(3) 2×[3+(-4)]=
2×3+2×(-4 ) =
(1) 2×(-3) = (-2 )×3=
-6
-6
24
24
-2
-2
2× (-3) (-2) ×3
[2×(-3)]×(- 4) 2×[(-3)×(-4)]
2×[3+(-4 )] 2×3+2×(-4 )
=
=
=
(-6)×(-4) =
2×12=
结论:
乘法运算律在有理数范围内仍然适用
(探究发现,学习新知)
探究新知
有理数的乘法法则
1
例1 计算
(1) (-4)×5×(-0.25);
解:
(1) 原式=[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=+5
(2) 原式=
有没有更加简便的方法?
自主探究
探究1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}算式
得数
负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
(2)有一个因数为 0 时,积是多少?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
有一个因数为 0 时,积是 0。
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
课堂练习
1.计算:
(1) ???????? ×(-???????????? ) ×(-????????????) ; (2) (-???????????????? )×(-???????????? ) ×0×???????? ;
?
解:
= 0
解:
(3) ???????? ×(-1.2) ×(-????????) ; (4) (-???????? )×(-???????? )×(-???????????? ) .
?
1.计算:
自主探究
例1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}算式
得数
负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
3.用乘法运算律简便计算:
(1)531×(-29)×(-2115)×(-412);
【解析】(1)????????????×(-????????)×(-2????????????)×(-4????????)
=[????????????×(-????????????????)]×[ (-????????×(-????????) ]
=-????????×1
=-????????;
?
(2) (-23)×37+(-23)×117.
【解析】(2) (-????????)×????????+(-????????)×????????????
=(-????????)×(????????+????????????)
=(-????????)×2
=-????????.
?
(10分钟·20分)
1.(3分·运算能力)下列算式中,运算结果为负数的是 ( )
A.0×(-5) B.4×(-3)×(-1)
C.(-1.5)×(-2)×(-3) D.(-2)×(-3)
2.(3分·运算能力)计算:100×(-3)×(-13)×0.01的结果是 ( )
A.1 B.-1 C.2 D.3
3.(4分·运算能力)计算:(-1)×(-9)×(-5)×(-19)=_______.?
4.(4分·运算能力·应用意识)用乘法分配律进行简便运算: (-334)×4= ____________
(只需写出接下来的一步,不必算出答案).?
?
素养当堂测评
C
A
5
?(-4+????????)×4
?
5.(6分·运算能力)运用有理数乘法运算律进行简便运算:
(1) (16-19-112)×36;
【解析】(1) (????????-????????-????????????)×36
=????????×36-????????×36-????????????×36=6-4-3=-1;
?
(2)492425×(-5).
【解析】(2)492425×(-5)
=(50-????????????)×(-5)
=-250+????????
=-?????????????????????.
?
你能看出下式的结果吗?如果能,请说明理由.
几个数相乘,如果其中有一个因数为 0,那么积等于____.
= 0
0
7.8×(-8.1)×0×(-19.6)
练一练
(2)有一个因数为 0 时,积是多少?
学以致用
5.计算:
(1)(-125)×(-2)×(-8);
(2)
(3)22×(-33)×(-4)×0.
(4)
解:(1)原式=-(125×2×8)
=-2 000.
(2)原式=?(????????????×????????????×????????)
=?????????.
?
解:(3)原式=0.
=-18.
(4)原式=?(????????×????×????????)
?
学以致用
6.计算:
学以致用
7.计算:
????????×????????×????????×????????×????????×????????×…×????????????????????????????????×????????????????????????????????×????????????????????????????????×????????????????????????????????
?
解:原式=????????×????????×????????×????????×????????×…×????????????????????????????????×????????????????????????????????×????????????????????????????????
=????????×1×1×…×1×????????????????????????????????
=????????????????????????????????
?
课堂小结
有理数的乘除运算2
多个有理数相乘的法则
有理数乘法的运算律
几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数.几个数相乘,有一个因数为0,则积为0.
乘法的交换律
乘法的结合律
乘法对加法的分配律
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
(既可以正用,也可以逆用)
探究一 多个有理数相乘的积的符号
[尝试交流]
计算:(1)(-4)×5×(-0.25);
解:(-4)×5×(-0.25)
=[-(4×5)]×(-0.25)
=(-20)×(-0.25)
=+(20×0.25)
=5.
(2)(-35)×(-56)×(-2).
?
解:(-35)×(-56)×(-2)
?
=[+(35×56) ]×(-2)
?
=12×(-2)
?
=-(12×2)
?
=-1.
[思考交流]
几个有理数相乘,因数都不为0时,积的符号怎样确定?有一个因数为0时,积是多少?
解:几个不等于0的有理数相乘,积的符号由负因数的个数决定,当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正.
几个数相乘,有一个因数为0,则积为0.
学 技巧
多个有理数相乘时积的符号确定
(1)几个不等于0的有理数相乘,积的符号由负因数的个数决
定,当负因数有奇数个时,积的符号为 ;当负因数有
偶数个时,积的符号为 .?
(2)几个数相乘,有一个因数为0,则积为 .?
负
正
0
变式2 计算:
(1)(-5)×(-145)×0.2×(-59);
(2)(-3.5+112-1)×(-10).
?
解:(1)原式=[(-5)×0.2]×[ (-95)×(-59)]=-1×1=-1.
?
(2)原式=(-3.5)×(-10)+32×(-10)-1×(-10)=35+(-15)-(-10)=
20+10=30.
?
【延伸拓展】
乘法对加法的分配律的逆应用
(1)将乘法对加法的分配律a(b+c)=ab+ac等号左右两边交换位置,得到ab+ac= .?
a(b+c)
(2)计算:
①6.868×(-17)+17×6.868;
②713×(-9)+713×(-18)+713.
?
解:①原式=6.868×(-17+17)=6.868×0=0.
②原式=713×[(-9)+(-18)+1]=713×(-26)=-14.
同课章节目录
