2.4 第三课时 有理数的除法 课件(共30张PPT) 2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4 第三课时 有理数的除法 课件(共30张PPT) 2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1018.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:39:15 | ||
图片预览









文档简介
(共30张PPT)
2.4 有理数的乘除运算
主讲:
第2章 有理数及其运算
第3课时
学习目标
1.理解有理数除法的法则,体会除法与乘法的关系;
2.会进行有理数的除法运算;(重点)
3.会求有理数的倒数,把有理数的除法运算转化乘法运算,体验转化的数学思想.(难点)
新课导入
2.有理数的乘法运算律
乘法的交换律:___________;
乘法的结合律:___________________;
乘法对加法的分配律:_____________________.
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
1.有理数乘法法则
两数相乘,同号得 ,异号得 ,绝对值相乘。任何数与0相乘,积为 .
正
负
0
复习回顾
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
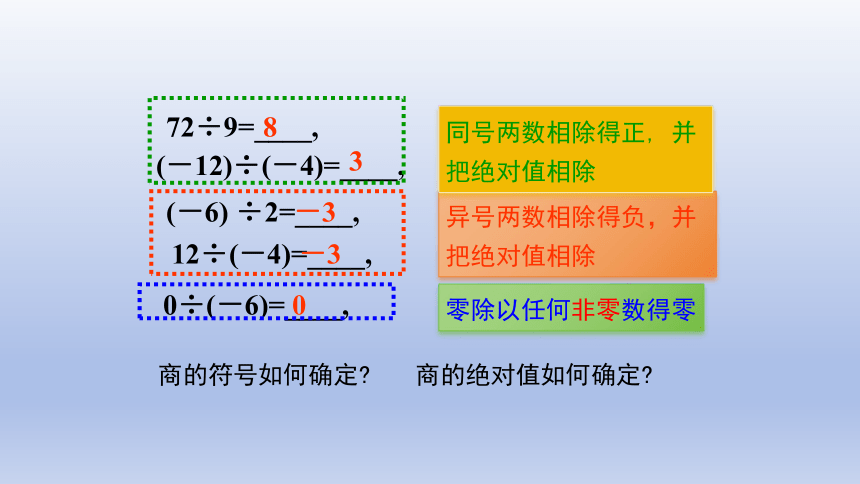
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
计算:
有理数的除法及分数化简
一
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
商的符号如何确定
商的绝对值如何确定
异号两数相除得负,并把绝对值相除
同号两数相除得正, 并把绝对值相除
零除以任何非零数得零
3
有理数的除法法则1
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何一个不等于0的数都得_____.
正
负
相除
0
0不能作为除数
注意
比较下列各组数计算结果:
15
除以一个数等于乘以这个数的倒数
做一做
(1)1÷(- )与1×(- )
(2)0.8÷(- )与0.8×(- )
(3)(- )÷(- )与(- )×(-60 )
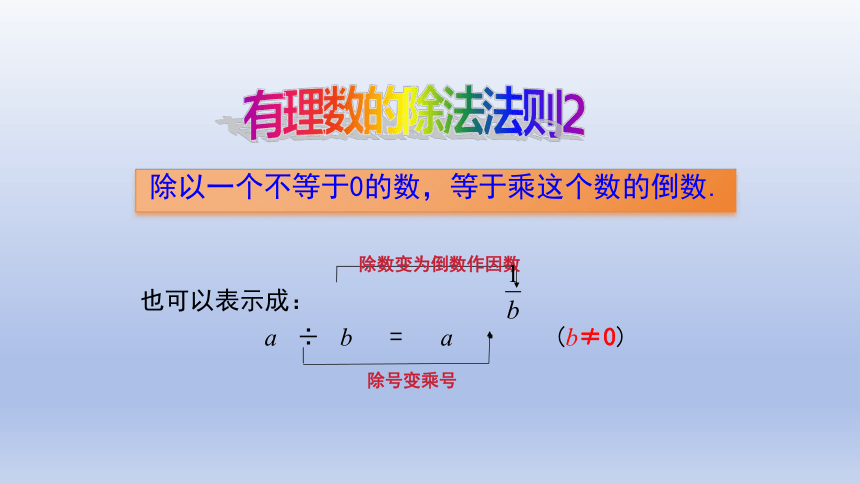
除以一个不等于0的数,等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
有理数的除法法则2
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
知识探究
尝试·交流
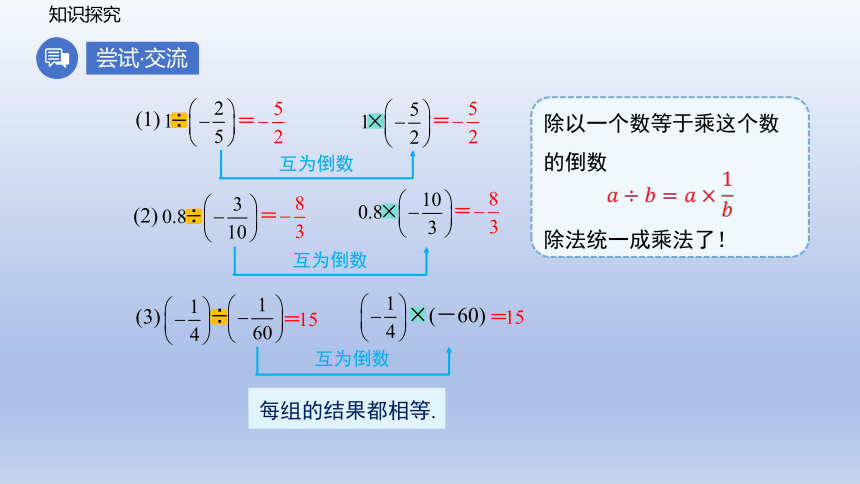
比较下列各组数的计算结果,你能得到什么结论?换一些算式再试一试,并与同伴进行交流
(1) 与
(2) 与
(3) ÷ 与 ×(-60)
知识探究
尝试·交流
(1)
(2)
(3) ÷
互为倒数
×(-60)
互为倒数
互为倒数
每组的结果都相等.
除以一个数等于乘这个数的倒数
除法统一成乘法了!
典型例题
例5 计算:
(1) (2)
解:(1)原式=
=
=27
(2) 原式
知识探究
1.选择原则:
能整除时直接相除,不能整除时应用除以一个数等于乘以该数的倒数.
有理数除法法则的选择和注意事项:
2.注意事项:
(1)应用直接相除时,要先确定符号,再确定绝对值.
(2)应用除以一个数等于乘以该数的倒数时,如果有小数或带分数,要化小数为分数,化带分数为假分数.
新知探究
针对练习
(1)
(2)
解:原式=
解:原式=
计算:
=
-
课堂小结
1.两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何非0的数都得0。
2.除以一个数等于乘这个数的倒数,即 。
二、有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
一、有理数除法法则:
1.下列计算正确的是( )
A. B.
C. D.
C
课堂训练
课堂训练
2. 计算:
(1) (-1.4)÷(-5.6);
(2) 8÷(-0.125);
解:原式 = -8×8 = -64.
解:原式 =
解:原式 =
课堂训练
3.填空:
(1)若 互为相反数,且 ,则 _______;
(2)当 时, =_______;
(3)若 则 的符号分别_____________.
(4)若﹣3x=12,则x=_______.
随堂练习
1.下列计算中,正确的是( )
A.-1÷1=0 B.2÷ =-4
C.5÷ =1 D.-3÷|-3|=1
B
2.下列运算中错误的是( )
A.
B.
C.8÷(-4)=-2
D.0÷(-3)=0
A
3.下列计算正确的是( )
A. B.
C. D.
C
4. 两个不等于0的有理数的和是0,则它们的商是( )
A.0 B.1 C.-1 D.1或-1
C
5.计算:
(1) ÷(-3); (2) ( )÷ ÷( );
(3)(-12)÷(-4)÷( ) .
6.计算:
解:原式=8×2
=16;
(2)(-36)÷(-4)÷(-9);
解:原式=9÷(-9)
=-1;
7.根据实验测定,高度每增加1 km,气温大约下降
5 ℃,某登山队员攀登某山峰的途中发回信息,报告他们所在高度的气温是-12 ℃,测得当时地面气温是3 ℃.请你确定登山运动员所在位置的高度.
解:[3-(-12)]÷5×1=3(km).
【能力练】
6.若 |x|=4,|y|=,且 xy<0,则 的值等于( )
A. 8 B.-8 C. 4 D. -4
【解析】根据题意得: x=±4,y=±,因为xy<0,所以x=4,y=-;x=-4,y=,则=-8.
7.(2024·宿迁期中)从-5,-3,-1,2,4这5个数中任取2个数,所得积的最大值记为a,所得商
的最小值记为b,则的值为_______.
【解析】因为最大值a=-5×(-3)=15,最小值b==-4,所以==-.
B
-
8.如果|a-2|+(b+4)2=0,那么=______.
【解析】因为|a-2|+(b+4)2=0,而|a-2|≥0,(b+4)2≥0,
所以a-2=0,b+4=0,解得a=2,b=-4,
所以==-.
-
【培优练】
9.(运算能力)阅读下列材料:
计算:50÷(-+).
解法一:原式=50÷-50÷+50÷
=50×3-50×4+50×12
=550.
解法二:原式=50÷
=50÷
=50×6
=300.
解法三:原式的倒数为÷50
=×
=×-×+×
=.
故原式=300.
上述解法得出的结果不同,其中肯定有错误的解法,你认为解法 是错误的.请你选择合适的解法解答下列问题:
计算:÷.
【解析】没有除法分配律,故解法一错误;
原式=÷=×3=-.
答案:一
谢谢大家欣赏
2.4 有理数的乘除运算
主讲:
第2章 有理数及其运算
第3课时
学习目标
1.理解有理数除法的法则,体会除法与乘法的关系;
2.会进行有理数的除法运算;(重点)
3.会求有理数的倒数,把有理数的除法运算转化乘法运算,体验转化的数学思想.(难点)
新课导入
2.有理数的乘法运算律
乘法的交换律:___________;
乘法的结合律:___________________;
乘法对加法的分配律:_____________________.
a×b=b×a
(a×b)×c=a×(b×c)
a×(b+c)=a×b+a×c
1.有理数乘法法则
两数相乘,同号得 ,异号得 ,绝对值相乘。任何数与0相乘,积为 .
正
负
0
复习回顾
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
计算:
有理数的除法及分数化简
一
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
商的符号如何确定
商的绝对值如何确定
异号两数相除得负,并把绝对值相除
同号两数相除得正, 并把绝对值相除
零除以任何非零数得零
3
有理数的除法法则1
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何一个不等于0的数都得_____.
正
负
相除
0
0不能作为除数
注意
比较下列各组数计算结果:
15
除以一个数等于乘以这个数的倒数
做一做
(1)1÷(- )与1×(- )
(2)0.8÷(- )与0.8×(- )
(3)(- )÷(- )与(- )×(-60 )
除以一个不等于0的数,等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
有理数的除法法则2
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
知识探究
尝试·交流
比较下列各组数的计算结果,你能得到什么结论?换一些算式再试一试,并与同伴进行交流
(1) 与
(2) 与
(3) ÷ 与 ×(-60)
知识探究
尝试·交流
(1)
(2)
(3) ÷
互为倒数
×(-60)
互为倒数
互为倒数
每组的结果都相等.
除以一个数等于乘这个数的倒数
除法统一成乘法了!
典型例题
例5 计算:
(1) (2)
解:(1)原式=
=
=27
(2) 原式
知识探究
1.选择原则:
能整除时直接相除,不能整除时应用除以一个数等于乘以该数的倒数.
有理数除法法则的选择和注意事项:
2.注意事项:
(1)应用直接相除时,要先确定符号,再确定绝对值.
(2)应用除以一个数等于乘以该数的倒数时,如果有小数或带分数,要化小数为分数,化带分数为假分数.
新知探究
针对练习
(1)
(2)
解:原式=
解:原式=
计算:
=
-
课堂小结
1.两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何非0的数都得0。
2.除以一个数等于乘这个数的倒数,即 。
二、有理数除法化为有理数乘法以后,可以利用有理数乘法的运算律简化运算.
一、有理数除法法则:
1.下列计算正确的是( )
A. B.
C. D.
C
课堂训练
课堂训练
2. 计算:
(1) (-1.4)÷(-5.6);
(2) 8÷(-0.125);
解:原式 = -8×8 = -64.
解:原式 =
解:原式 =
课堂训练
3.填空:
(1)若 互为相反数,且 ,则 _______;
(2)当 时, =_______;
(3)若 则 的符号分别_____________.
(4)若﹣3x=12,则x=_______.
随堂练习
1.下列计算中,正确的是( )
A.-1÷1=0 B.2÷ =-4
C.5÷ =1 D.-3÷|-3|=1
B
2.下列运算中错误的是( )
A.
B.
C.8÷(-4)=-2
D.0÷(-3)=0
A
3.下列计算正确的是( )
A. B.
C. D.
C
4. 两个不等于0的有理数的和是0,则它们的商是( )
A.0 B.1 C.-1 D.1或-1
C
5.计算:
(1) ÷(-3); (2) ( )÷ ÷( );
(3)(-12)÷(-4)÷( ) .
6.计算:
解:原式=8×2
=16;
(2)(-36)÷(-4)÷(-9);
解:原式=9÷(-9)
=-1;
7.根据实验测定,高度每增加1 km,气温大约下降
5 ℃,某登山队员攀登某山峰的途中发回信息,报告他们所在高度的气温是-12 ℃,测得当时地面气温是3 ℃.请你确定登山运动员所在位置的高度.
解:[3-(-12)]÷5×1=3(km).
【能力练】
6.若 |x|=4,|y|=,且 xy<0,则 的值等于( )
A. 8 B.-8 C. 4 D. -4
【解析】根据题意得: x=±4,y=±,因为xy<0,所以x=4,y=-;x=-4,y=,则=-8.
7.(2024·宿迁期中)从-5,-3,-1,2,4这5个数中任取2个数,所得积的最大值记为a,所得商
的最小值记为b,则的值为_______.
【解析】因为最大值a=-5×(-3)=15,最小值b==-4,所以==-.
B
-
8.如果|a-2|+(b+4)2=0,那么=______.
【解析】因为|a-2|+(b+4)2=0,而|a-2|≥0,(b+4)2≥0,
所以a-2=0,b+4=0,解得a=2,b=-4,
所以==-.
-
【培优练】
9.(运算能力)阅读下列材料:
计算:50÷(-+).
解法一:原式=50÷-50÷+50÷
=50×3-50×4+50×12
=550.
解法二:原式=50÷
=50÷
=50×6
=300.
解法三:原式的倒数为÷50
=×
=×-×+×
=.
故原式=300.
上述解法得出的结果不同,其中肯定有错误的解法,你认为解法 是错误的.请你选择合适的解法解答下列问题:
计算:÷.
【解析】没有除法分配律,故解法一错误;
原式=÷=×3=-.
答案:一
谢谢大家欣赏
同课章节目录
