2.4 第三课时 有理数的除法 课件(共26张PPT)2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4 第三课时 有理数的除法 课件(共26张PPT)2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:37:49 | ||
图片预览






文档简介
(共26张PPT)
第二章 有理数及其运算
2.4 有理数的乘除运算
第3课时 有理数的除法
创设情境 探究与应用 课堂小结与检测
【课堂引入】
创设情境
1.前面我们学习了有理数的乘法,你还记得有理数的乘法法则是什么吗
2.小学里乘法与除法互为逆运算,有被除数÷除数=商的关系.那么有理数的除法又如何来计算呢
两数相乘,同号得正、异号得负,并把绝对值相乘;
任何数与0相乘,积仍为0.
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
计算:
有理数的除法及分数化简
知识点1:
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
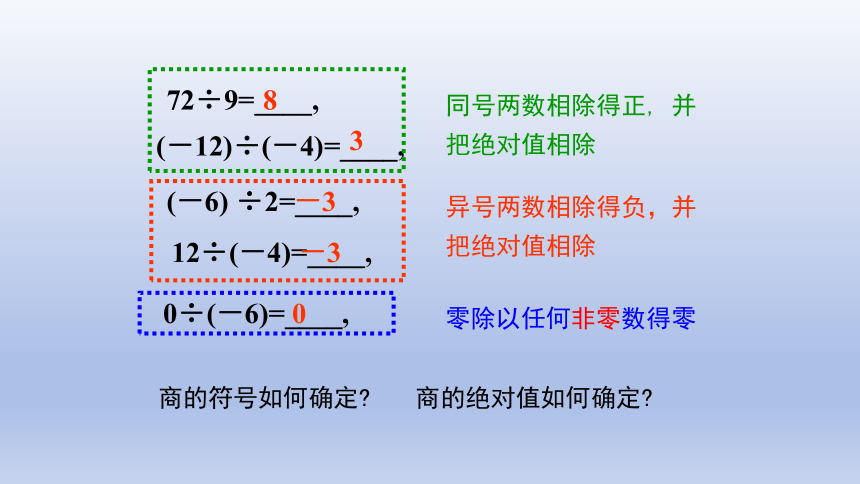
商的符号如何确定
商的绝对值如何确定
异号两数相除得负,并把绝对值相除
同号两数相除得正, 并把绝对值相除
零除以任何非零数得零
3
有理数的除法法则1
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何非0的数都得_____.
正
负
相除
0
0不能作除数
注意
(-12)÷( )÷(-100)
下面两种计算正确吗 请说明理由:
(1)解:原式=(-12)÷( ÷100)
=(-12)÷ =-14400
(2)解:原式=( )÷(-12)÷(-100)
= ÷(-100)=
除法不适合交换律与结合律,所以不正确.
(×)
(×)
想一想
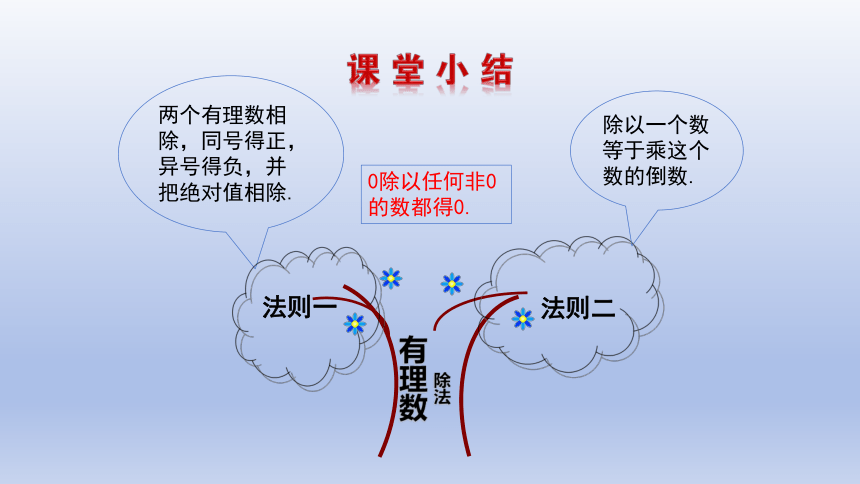
两个有理数相除,同号得正,异号得负,并把绝对值相除.
法则一
法则二
除法
有理数
0除以任何非0的数都得0.
除以一个数等于乘这个数的倒数.
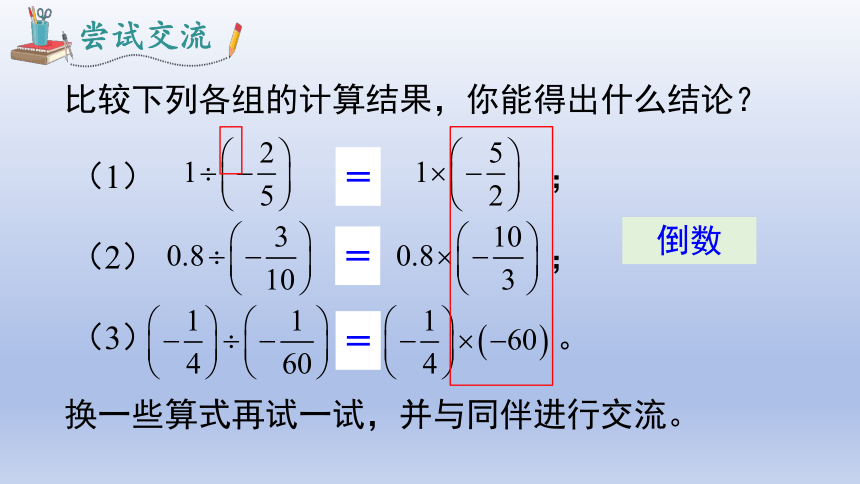
尝试交流
比较下列各组的计算结果,你能得出什么结论?
换一些算式再试一试,并与同伴进行交流。
(1) 与 ;
(2) 与 ;
(3) 与 。
=
=
=
倒数
定义总结
用字母表示为:
除以一个不等于 0 的数,等于乘这个数的倒数.
除法统一成乘法了!
典例精析
例2 计算:
(1) ; (2) 。
解:(1) ;
(2)
。
1. 计算:
(2) 原式 =
(1) (内蒙古校考)
解:(1) 原式 =
= 3.
带分数和小数可化为分数计算
练一练
方法归纳交流 (1)一般来说,在什么情况下选择法则(一) 什么情况下选择法则(二)
解:一般来说,能整除的情况下,往往采用法则(一),在确定符号后,直接除.在不能整除的情况下,则往往将除数换成倒数,转化为乘法.
(2)类比有理数减法法则,在有理数除法法则(二)中,也有两“变”,一是运算符号的变化,即由“÷”变“ ”,二是除数变为它的 .用下面的图示加以说明:
倒数
×
有理数除法的应用
例 一人乘热气球旅行,在地面时测得温度是8 ℃,当热气球升空后,测得高空的温度是-1 ℃ ,求此时热气球的高度.(已知该地海拔每升高1000米,气温下降6 ℃)
解:8-(-1)=9(℃),9÷6=1.5,1.5×1000=1500(米).
此时热气球的高度为1500米.
变式训练
一天,小红与小丽利用温差测量山的高度,小红在山顶测得温度是-4 ℃,小丽此时在山脚测得温度是6 ℃.已知该地区高度每增加100米,气温大约降低0.8 ℃,这个山峰大约有多少米
解:根据题意得[6-(-4)]÷0.8×100=1250(米).
答:这个山峰的高度大约是1250米.
1.已知43×49=2107,则(-43)÷的值为 ( )
A.2107 B.-2107
C. D.-
B
2.计算(-1)÷3× - 的结果是 .
1.计算(-6)÷18的结果是( C )
A.-3
B.3
C.-
D.
C
基础提能
2.下列运算错误的是( D )
A.0÷(-3)=0
B.-5÷(-)=-5×(-2)
C.8÷(-2)=8×(-)
D.÷(-3)=3×(-3)
D
3.计算1÷(-3)时,除法变为乘法正确的是( D )
A.1×(-3)
B.1×(+)
C.1×(+)
D.1×(-)
D
4.计算:
(1)(-5)÷;
(1)解:原式=(-5)×2=-10.
(2)14÷(-);
(2)解:原式=14×(-)=-.
(3)(-2.5)÷(-).
解:原式=(-)×(-)=4.
5.两个因数的积为1,其中一个因数是-2,则另一个因数是 - .
-
四、当堂练习
2.下列说法正确的是( )
A.任何有理数都有倒数 B.一个数的倒数小与它本身
C.0除以任何数都得0 D.两个数的商为0,只有被除数为0
1.已知有两个有理数的商为负数,那么( )
A.它们的和为负数 B.它们的差为负数
C.它们的积为负数 D.它们的积为正数
C
D
4.两个因数的积为1,已知其中一个因数为-,那么另一个因数是 .
四、当堂练习
A
5
四、当堂练习
四、当堂练习
第二章 有理数及其运算
2.4 有理数的乘除运算
第3课时 有理数的除法
创设情境 探究与应用 课堂小结与检测
【课堂引入】
创设情境
1.前面我们学习了有理数的乘法,你还记得有理数的乘法法则是什么吗
2.小学里乘法与除法互为逆运算,有被除数÷除数=商的关系.那么有理数的除法又如何来计算呢
两数相乘,同号得正、异号得负,并把绝对值相乘;
任何数与0相乘,积仍为0.
2×(-3)=____ ,
(-4)×(-3)=____,
8×9=____,
0×(-6)=____,
(-4)×3 =____ ,
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
观察右侧算式, 两个有理数相除时:
商的符号如何确定
商的绝对值如何确定
-6
12
72
-12
0
-3
-3
8
0
3
计算:
有理数的除法及分数化简
知识点1:
(-6) ÷2=____,
12÷(-4)=____,
72÷9=____,
(-12)÷(-4)=____,
0÷(-6)=____,
-3
-3
8
0
商的符号如何确定
商的绝对值如何确定
异号两数相除得负,并把绝对值相除
同号两数相除得正, 并把绝对值相除
零除以任何非零数得零
3
有理数的除法法则1
两个有理数相除, 同号得____,
异号得_____,并把绝对值_______.
0除以任何非0的数都得_____.
正
负
相除
0
0不能作除数
注意
(-12)÷( )÷(-100)
下面两种计算正确吗 请说明理由:
(1)解:原式=(-12)÷( ÷100)
=(-12)÷ =-14400
(2)解:原式=( )÷(-12)÷(-100)
= ÷(-100)=
除法不适合交换律与结合律,所以不正确.
(×)
(×)
想一想
两个有理数相除,同号得正,异号得负,并把绝对值相除.
法则一
法则二
除法
有理数
0除以任何非0的数都得0.
除以一个数等于乘这个数的倒数.
尝试交流
比较下列各组的计算结果,你能得出什么结论?
换一些算式再试一试,并与同伴进行交流。
(1) 与 ;
(2) 与 ;
(3) 与 。
=
=
=
倒数
定义总结
用字母表示为:
除以一个不等于 0 的数,等于乘这个数的倒数.
除法统一成乘法了!
典例精析
例2 计算:
(1) ; (2) 。
解:(1) ;
(2)
。
1. 计算:
(2) 原式 =
(1) (内蒙古校考)
解:(1) 原式 =
= 3.
带分数和小数可化为分数计算
练一练
方法归纳交流 (1)一般来说,在什么情况下选择法则(一) 什么情况下选择法则(二)
解:一般来说,能整除的情况下,往往采用法则(一),在确定符号后,直接除.在不能整除的情况下,则往往将除数换成倒数,转化为乘法.
(2)类比有理数减法法则,在有理数除法法则(二)中,也有两“变”,一是运算符号的变化,即由“÷”变“ ”,二是除数变为它的 .用下面的图示加以说明:
倒数
×
有理数除法的应用
例 一人乘热气球旅行,在地面时测得温度是8 ℃,当热气球升空后,测得高空的温度是-1 ℃ ,求此时热气球的高度.(已知该地海拔每升高1000米,气温下降6 ℃)
解:8-(-1)=9(℃),9÷6=1.5,1.5×1000=1500(米).
此时热气球的高度为1500米.
变式训练
一天,小红与小丽利用温差测量山的高度,小红在山顶测得温度是-4 ℃,小丽此时在山脚测得温度是6 ℃.已知该地区高度每增加100米,气温大约降低0.8 ℃,这个山峰大约有多少米
解:根据题意得[6-(-4)]÷0.8×100=1250(米).
答:这个山峰的高度大约是1250米.
1.已知43×49=2107,则(-43)÷的值为 ( )
A.2107 B.-2107
C. D.-
B
2.计算(-1)÷3× - 的结果是 .
1.计算(-6)÷18的结果是( C )
A.-3
B.3
C.-
D.
C
基础提能
2.下列运算错误的是( D )
A.0÷(-3)=0
B.-5÷(-)=-5×(-2)
C.8÷(-2)=8×(-)
D.÷(-3)=3×(-3)
D
3.计算1÷(-3)时,除法变为乘法正确的是( D )
A.1×(-3)
B.1×(+)
C.1×(+)
D.1×(-)
D
4.计算:
(1)(-5)÷;
(1)解:原式=(-5)×2=-10.
(2)14÷(-);
(2)解:原式=14×(-)=-.
(3)(-2.5)÷(-).
解:原式=(-)×(-)=4.
5.两个因数的积为1,其中一个因数是-2,则另一个因数是 - .
-
四、当堂练习
2.下列说法正确的是( )
A.任何有理数都有倒数 B.一个数的倒数小与它本身
C.0除以任何数都得0 D.两个数的商为0,只有被除数为0
1.已知有两个有理数的商为负数,那么( )
A.它们的和为负数 B.它们的差为负数
C.它们的积为负数 D.它们的积为正数
C
D
4.两个因数的积为1,已知其中一个因数为-,那么另一个因数是 .
四、当堂练习
A
5
四、当堂练习
四、当堂练习
同课章节目录
