2.4 第三课时有理数的除法 课件(共27张PPT) 2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4 第三课时有理数的除法 课件(共27张PPT) 2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 16:46:43 | ||
图片预览







文档简介
(共27张PPT)
2.4有理数的乘除运算
(第3课时)
第二章 有理数及其运算
学习目标
理解有理数的除法法则,体会除法与乘法的关系
01
掌握有理数除法的运算方法
02
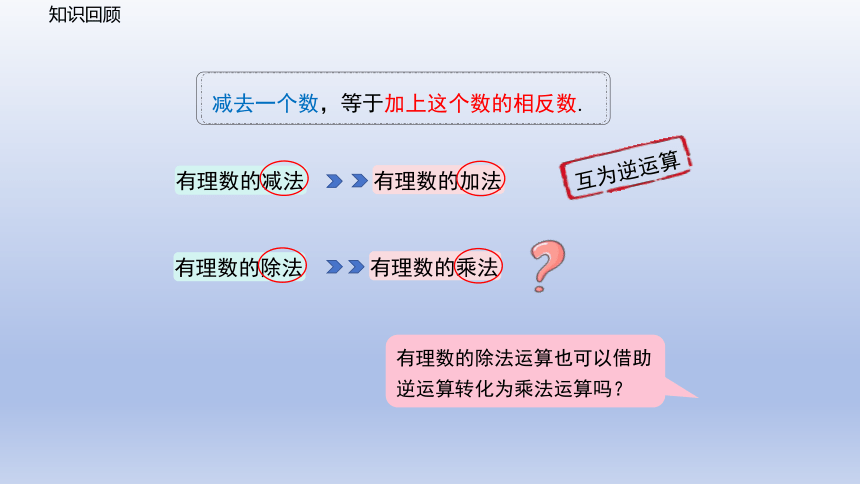
知识回顾
减去一个数,等于加上这个数的相反数.
有理数的减法
有理数的加法
互为逆运算
有理数的除法
有理数的乘法
有理数的除法运算也可以借助逆运算转化为乘法运算吗?
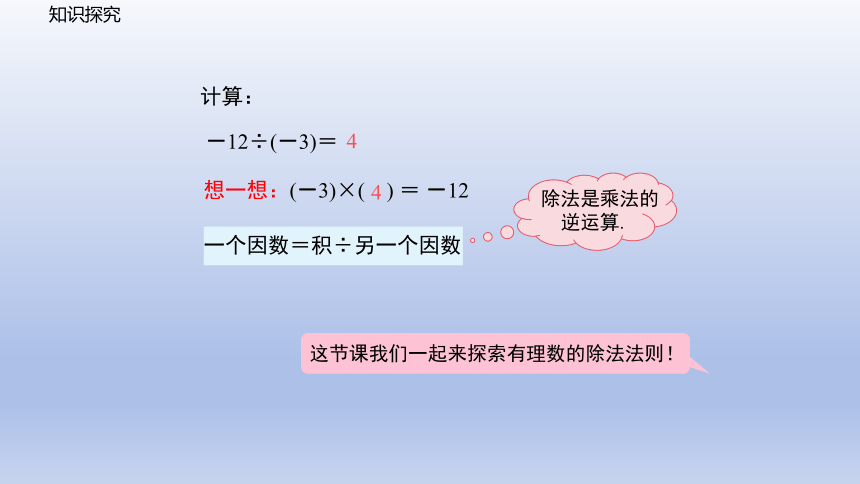
知识探究
计算:
想一想:(-3)×( ) = -12
-12÷(-3)=
一个因数=积÷另一个因数
4
4
除法是乘法的
逆运算.
这节课我们一起来探索有理数的除法法则!
填一填:
①由(-3)×(-4)=12 计算:12÷(-3)=______ ;
12÷(-4)=______
②由(-3)×4=-12 计算:(-12)÷(-3)=_____;
由3×(-4)=-12 计算: (-12)÷(-4)=____;
③由0×(-2)=0 计算: 0÷(-2)=_______。
-4
-3
4
3
0
根据乘法和除法互为逆运算,我们很容易求出以上各式的结果。
新知探究
知识点 有理数的除法法则
1
(-18)÷6=____
(-27)÷(-9)=___
5÷(- )=____
1
5
0÷(-2)=____
想一想:你能直接求出下列各式的结果吗?你是怎么计算的?
从以上算式,你能归纳出有理数的除法有什么特点与规律吗?
-3
-25
3
0
新知探究
新知探究
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何非0的数都得0。
有理数除法法则(一):
归纳总结
注意:0不能作除数。
例1 计算:
(1)(-15)÷(-3)
(2)
确定符号:同号得正
=5
解:原式=+
绝对值相除
=-48
解:原式=-
确定符号:异号得负
绝对值相除
(15÷3)
新知探究
典型例题
(3) (-0.75)÷0.25
(4) (-12)÷
确定符号:异号得负
=-3
解:原式=-
绝对值相除
=144÷(-100)
解:原式=+
=- (144÷100)
=-1.44
多个有理数相除时,按照两数相除的法则依次计算
(0.75÷0.25)
新知探究
【探究2】将除法转化为乘法
【尝试·交流】
探究与应用
比较下列各组数的计算结果,你能得到什么结论 换一些算式再试一试,并与同伴进行交流.
(1)1÷(-)与1×(-); (2)0.8÷(-)与0.8×(-);
(3)(-)÷(-)与(-)×(-60).
1÷(-)=1×(-);
0.8÷(-)=0.8×(-)
(-)÷(-)=(-)×(-60).
【探究2】将除法转化为乘法
【尝试·交流】
探究与应用
根据刚才的计算,想一想:如何计算有理数的除法?
【概括新知】
除以一个数等于乘这个数的倒数.
除以一个数等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
有理数的除法法则2
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
例2 计算(1)(-36)÷9;
(2) .
(2)原式=
典例精析
解:(1)原式= - (36÷ 9)= - 4;
-4
-8
0
计算:
练一练
【探究2】将除法转化为乘法
【应用】
探究与应用
例 (教材例5)计算:
(1)(-18)÷(-); (2)16÷(-)÷(-).
=(-18)×(-
= 18×
= 27
=16(- ))
= 16×
=
注意:方法不唯一哟
【探究2】将除法转化为乘法
【思考·交流】
探究与应用
(1)将除法转化为乘法有什么好处
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点 与同伴进行交流.
便于约分,从而使计算简便
相同点:计算方法相同
不同点:有理数的乘除法,要先确定积(或商)的符号,再确定积(或商)的绝对值;而小学数学中的乘除法中,是正数和正数或0和正数之间的运算,所得的结果非正即0.
【拓展提升】
探究与应用
1.计算9÷(-3)×的结果为 ( )
A.-1 B.1 C.9 D.-9
2.计算-4÷÷16×(-)的结果为 ( )
A.-1 B. C. D.1
3.填空:(1)当a 时,=1;当a 时,=-1.
(2)当m= 时,2÷(3m+1)没有意义; 当n= 时,(1-2n)÷11=0.
(3)两数的积是-1,如果其中一个数是-,那么另一个数是 .
A
B
>0
<0
-
随堂练习
1.计算:
(1)
(2)
(3)
(4)
答案
一、做一做:
先说出商的符号,再说出商:
(1) 12÷4 (2)(-57)÷3
(3)(-36)÷(-9) (4)96 ÷(-16)
=3
=-19
= 4
=-6
二、试一试:
根据以往的知识,你能否说出下列各数的倒数:
那么零的倒数呢?零有没有倒数?
2
-4
-1
没有。
巩固提高
巩固提高
解:原式
解:原式
三、计算:
四、填空.
(1) 的倒数是-2, -0.1的倒数是 .
(2)-6的倒数是 ,相反数是 .
(3) 的倒数等于它本身, 的相反数
等于它本身, 的绝对值等于它本身.
(4)若一个数的相反数与这个数的倒数的和等于0,则这
个数是 .
-10
6
0
非负数
巩固提高
6÷(-3)=-2
新知识
旧知识
转化
小 结
互为倒数
相同的结果
-3
6×(- )=-2
1
3
1
3
-
7.某冷冻厂一个冷库的室温是-1 ℃,现有一批食品需在-19 ℃的温度下冷藏,如果每小时降温3 ℃,那么 6 小时后才能降到所需的温度.
6
8.【易错题】计算:(-24)÷6×.
解:原式=(-24)××
=-(24××)=-.
9.分类讨论求++的值.
解:当a,b,c都是正数时,
++=1+1+1=3.
当a,b,c有两个正数时,
++=1+1-1=1.
当a,b,c有一个正数时,
++=1-1-1=-1.
当a,b,c都是负数时,
++=-1-1-1=-3.
综上所述,++的值是±3或±1.
8.比较两个同号的有理数a和b的大小,可以按照如下方法进行:
若a>0,b>0,且>1,则a>b;
若a<0,b<0,>1,则a<b.
以上这种比较大小的方法叫做作商比较法.
试用作商比较法比较-与-的大小.
解:因为-<0,-<0,=(-)÷(-)=(-)×(-)=,
所以=>1.所以-<-.
2.4有理数的乘除运算
(第3课时)
第二章 有理数及其运算
学习目标
理解有理数的除法法则,体会除法与乘法的关系
01
掌握有理数除法的运算方法
02
知识回顾
减去一个数,等于加上这个数的相反数.
有理数的减法
有理数的加法
互为逆运算
有理数的除法
有理数的乘法
有理数的除法运算也可以借助逆运算转化为乘法运算吗?
知识探究
计算:
想一想:(-3)×( ) = -12
-12÷(-3)=
一个因数=积÷另一个因数
4
4
除法是乘法的
逆运算.
这节课我们一起来探索有理数的除法法则!
填一填:
①由(-3)×(-4)=12 计算:12÷(-3)=______ ;
12÷(-4)=______
②由(-3)×4=-12 计算:(-12)÷(-3)=_____;
由3×(-4)=-12 计算: (-12)÷(-4)=____;
③由0×(-2)=0 计算: 0÷(-2)=_______。
-4
-3
4
3
0
根据乘法和除法互为逆运算,我们很容易求出以上各式的结果。
新知探究
知识点 有理数的除法法则
1
(-18)÷6=____
(-27)÷(-9)=___
5÷(- )=____
1
5
0÷(-2)=____
想一想:你能直接求出下列各式的结果吗?你是怎么计算的?
从以上算式,你能归纳出有理数的除法有什么特点与规律吗?
-3
-25
3
0
新知探究
新知探究
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何非0的数都得0。
有理数除法法则(一):
归纳总结
注意:0不能作除数。
例1 计算:
(1)(-15)÷(-3)
(2)
确定符号:同号得正
=5
解:原式=+
绝对值相除
=-48
解:原式=-
确定符号:异号得负
绝对值相除
(15÷3)
新知探究
典型例题
(3) (-0.75)÷0.25
(4) (-12)÷
确定符号:异号得负
=-3
解:原式=-
绝对值相除
=144÷(-100)
解:原式=+
=- (144÷100)
=-1.44
多个有理数相除时,按照两数相除的法则依次计算
(0.75÷0.25)
新知探究
【探究2】将除法转化为乘法
【尝试·交流】
探究与应用
比较下列各组数的计算结果,你能得到什么结论 换一些算式再试一试,并与同伴进行交流.
(1)1÷(-)与1×(-); (2)0.8÷(-)与0.8×(-);
(3)(-)÷(-)与(-)×(-60).
1÷(-)=1×(-);
0.8÷(-)=0.8×(-)
(-)÷(-)=(-)×(-60).
【探究2】将除法转化为乘法
【尝试·交流】
探究与应用
根据刚才的计算,想一想:如何计算有理数的除法?
【概括新知】
除以一个数等于乘这个数的倒数.
除以一个数等于乘这个数的倒数.
也可以表示成:
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
有理数的除法法则2
对比记忆
有理数的减法法则
减去一个数,等于加这个数的相反数.
a - b = a + (-b)
减数变为相反数作加数
减号变加号
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为倒数作因数
例2 计算(1)(-36)÷9;
(2) .
(2)原式=
典例精析
解:(1)原式= - (36÷ 9)= - 4;
-4
-8
0
计算:
练一练
【探究2】将除法转化为乘法
【应用】
探究与应用
例 (教材例5)计算:
(1)(-18)÷(-); (2)16÷(-)÷(-).
=(-18)×(-
= 18×
= 27
=16(- ))
= 16×
=
注意:方法不唯一哟
【探究2】将除法转化为乘法
【思考·交流】
探究与应用
(1)将除法转化为乘法有什么好处
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点 与同伴进行交流.
便于约分,从而使计算简便
相同点:计算方法相同
不同点:有理数的乘除法,要先确定积(或商)的符号,再确定积(或商)的绝对值;而小学数学中的乘除法中,是正数和正数或0和正数之间的运算,所得的结果非正即0.
【拓展提升】
探究与应用
1.计算9÷(-3)×的结果为 ( )
A.-1 B.1 C.9 D.-9
2.计算-4÷÷16×(-)的结果为 ( )
A.-1 B. C. D.1
3.填空:(1)当a 时,=1;当a 时,=-1.
(2)当m= 时,2÷(3m+1)没有意义; 当n= 时,(1-2n)÷11=0.
(3)两数的积是-1,如果其中一个数是-,那么另一个数是 .
A
B
>0
<0
-
随堂练习
1.计算:
(1)
(2)
(3)
(4)
答案
一、做一做:
先说出商的符号,再说出商:
(1) 12÷4 (2)(-57)÷3
(3)(-36)÷(-9) (4)96 ÷(-16)
=3
=-19
= 4
=-6
二、试一试:
根据以往的知识,你能否说出下列各数的倒数:
那么零的倒数呢?零有没有倒数?
2
-4
-1
没有。
巩固提高
巩固提高
解:原式
解:原式
三、计算:
四、填空.
(1) 的倒数是-2, -0.1的倒数是 .
(2)-6的倒数是 ,相反数是 .
(3) 的倒数等于它本身, 的相反数
等于它本身, 的绝对值等于它本身.
(4)若一个数的相反数与这个数的倒数的和等于0,则这
个数是 .
-10
6
0
非负数
巩固提高
6÷(-3)=-2
新知识
旧知识
转化
小 结
互为倒数
相同的结果
-3
6×(- )=-2
1
3
1
3
-
7.某冷冻厂一个冷库的室温是-1 ℃,现有一批食品需在-19 ℃的温度下冷藏,如果每小时降温3 ℃,那么 6 小时后才能降到所需的温度.
6
8.【易错题】计算:(-24)÷6×.
解:原式=(-24)××
=-(24××)=-.
9.分类讨论求++的值.
解:当a,b,c都是正数时,
++=1+1+1=3.
当a,b,c有两个正数时,
++=1+1-1=1.
当a,b,c有一个正数时,
++=1-1-1=-1.
当a,b,c都是负数时,
++=-1-1-1=-3.
综上所述,++的值是±3或±1.
8.比较两个同号的有理数a和b的大小,可以按照如下方法进行:
若a>0,b>0,且>1,则a>b;
若a<0,b<0,>1,则a<b.
以上这种比较大小的方法叫做作商比较法.
试用作商比较法比较-与-的大小.
解:因为-<0,-<0,=(-)÷(-)=(-)×(-)=,
所以=>1.所以-<-.
同课章节目录
