2.4有理数的乘除运算 第三课时 有理数的除法 课件(35张ppt)2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4有理数的乘除运算 第三课时 有理数的除法 课件(35张ppt)2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 17:22:42 | ||
图片预览








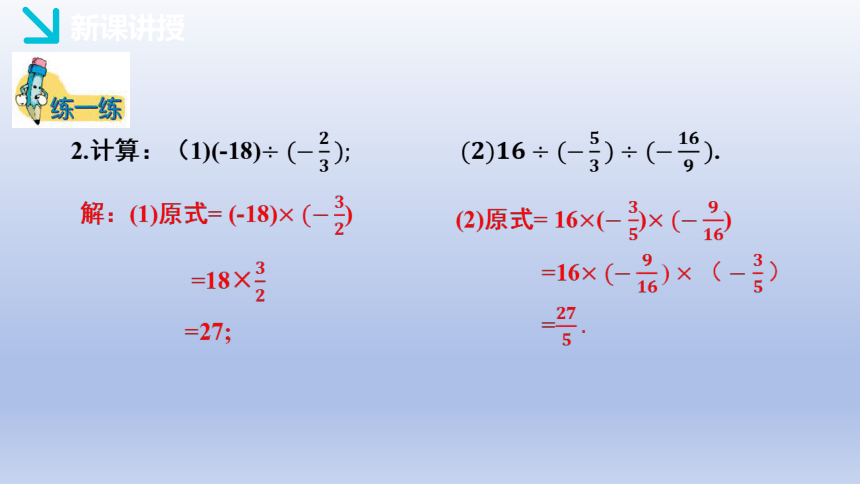


文档简介
第3课时 有理数除法法则
第二章 有理数及其运算
2.4 有理数的乘除运算
1.理解有理数除法法则,体会除法与乘法的联系。
2.会利用有理数除法法则进行有理数的除法运算。
学习目标
情境导入
除法与乘法是互逆运算,在小学我们就认识到除法与乘法相互转化可以简化运算,那么在有理数范围内,又怎样将除法转化成乘法?有理数的除法可以怎样进行计算呢?
(-12)÷(-3)=?你能得出结果吗?
被除数=除数×商
那么:-12=(-3 ) × ?
我们知道只有:(-3)× 4 =-12
所以(-12)÷(-3)=4
知识点1
教学过程
在小学我们就已经知道,乘法与除法互为逆运算,为了计算(?????????)÷4,我们必须找到一个数与????相乘等于?????????.
?
因为(?????)×????=?????????, 所以(?????????)÷????=?????
?
.
有理数除法法则(1)
知识点1
教学过程
有理数除法法则(1)
利用乘法与除法互为逆运算,计算下面各题:
(1) (?????????)÷(?????), (????) (?????????)÷(?????),
(????) (?????????)÷????, (????) ????????÷(?????????) ,
(????) ????÷???????? , (????) ????÷(?????????)。
?
.
知识点1
教学过程
利用乘法与除法互为逆运算,计算下面各题:
.
想一想:两个有理数相除,商的符号与除数和被除数的符号有什么关系?
(1) (?????????)÷(?????)=????;
?
.
(????) (?????????)÷(?????)=????;
?
.
(????) (?????????)÷????=?????;
?
.
(????) ????????÷(?????????)=????? ;
?
.
(????) ????÷????????=???? ;
?
.
(????) ????÷(?????????)=???? ;
?
.
有理数除法法则(1)
知识点1
教学过程
由此我们得到有理数除法法则:
.
有理数除法法则(1)
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何数都是得0。
注意:0不能作除数。
?
有理数除法法则(1)
学以致用
教学过程
计算:
.
.
.
(1) (?????????????)÷(?????????), (????) ????????÷(?????????),
?
.
新课讲授
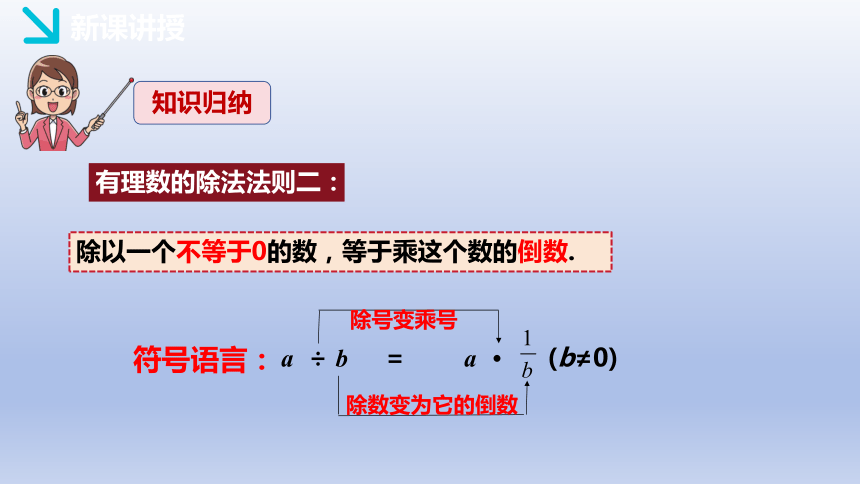
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为它的倒数
符号语言:
有理数的除法法则二:
知识归纳
新课讲授
2.计算:(1)(-18)÷(?????????); (????)????????÷(?????????)÷(?????????????).
?
解:(1)原式= (-18)×(?????????)
=18×????????
=27;
?
(2)原式= 16×(?????????)×(?????????????)
=16×(?????????????)×(?????????)
=????????????.
?
新课讲授
方法归纳
有理数除法运算的方法:
1.对于只有除法的运算,有括号先算括号内,无括号就从左到右运算;
2.可以先把所有除法都变成乘法,然后再用乘法交换律和结合律.
新课讲授
思考·交流:
(1)将除法转化为乘法有什么好处?
将除法转化为乘法的主要好处包括简化计算过程、节约时间、提高计算效率;
相同点:都是整数与分数的运算,大部分知识是在小学就学过了.
不同点:初中有理数运算新增了一些乘法公式,并且运算起来比小学的复杂,有时还会用字母表示数,用复杂的代数式运算.
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点?与同伴进行交流。
5.【阅读材料】定义:如果两个有理数的差等于这两个有理数的商,那么这两个有理数就叫作“差商等数对”.即:如果a-b=a÷b,那么a与b就叫作“差商等数对”,记为(a,b).例如:4-2=4÷2,????????-3=????????÷3,则称数对(4,2),????????,????是“差商等数对”.
【动手解决】下列数对中,是“差商等数对”的是 .(选填序号)?
①????????,?????; ②????????????,????.
?
②
1.21÷(-7)的结果是( )
A.3 B.-3 C.???????? D.-????????
2.与-2的乘积为1的数是( )
A.2 B.-2 C.???????? D.-????????
?
B
D
3.与2÷3÷4运算结果相同的是( )
A.2÷(3÷4) B.2÷(3×4)
C.2÷(4÷3) D.3÷2÷4
4.计算:(1)(-8)÷?????????= ;?
(2)(-1)÷(-6)÷?????????= .?
?
B
32
-1
5.小明星期天到体育用品商店购买一个排球花了36元.已知排球按标价打八折,那么排球的标价是 元.?
45
6.计算:
(1)(-5)÷?????????????×????????×?????????????÷7; (2)?????????????????+????????÷????????????.
?
(1)-????????.
?
(2)1.
随 堂 训 练
1.计算 的结果正确的是 ( )
C
C
2.计算-15÷(-5)的结果正确的是( )
A.75 B.-75 C.3 D.-3
4.算式 中的括号内应填上 ( )
D
?
A
随堂训练
1. 规定一种新的运算:A★B=A×B-A÷B,如4★2=4×2-4÷2=6,则6★(-3)的值为 .
-16
课后提升
?
?
D
B
A
B
有理数的除法法则:
有理数除法的计算方法:
有理数的除法
同号得正,异号得负,并把绝对值相除;
0 除以任何一个非 0 的数都得 0.
除以一个数,等于乘这个数的倒数.
整数的除法,先确定符号,并把两数的绝对值相除.
有分数或小数参与的运算,将除法转化为乘法,确定结果符号后再计算,一般情况下会比较简便.
已知非零有理数 a , b , c 满足 a + b + c =0,试求 |????|???? +
????|????| + ????|????| + |????????????|???????????? 的值.
?
【思路导航】因为 a , b , c 非零且和为0,所以 a , b , c 中有
两正一负或两负一正,所以可分情况得到 |????|???? , ????|????| ,
????|????| , |????????????|???????????? 中有几个-1和1,从而求出 |????|???? + ????|????| +
????|????| + |????????????|???????????? 的值.
?
解:因为 a , b , c 为非零有理数,且 a + b + c =0,
所以 a , b , c 中有两正一负或两负一正.
①当 a , b , c 中有两正一负时, abc <0,则 |????????????|???????????? =-1,
|????|???? , ????|????| , ????|????| 中有两个等于1,一个等于-1,
故 |????|???? + ????|????| + ????|????| + |????????????|???????????? =0;
?
②当 a , b , c 中有两负一正时, abc >0,则 |????????????|???????????? =1,
|????|???? , ????|????| , ????|????| 中有一个等于1,两个等于-1,
故 |????|???? + ????|????| + ????|????| + |????????????|???????????? =0.
综上所述, |????|???? + ????|????| + ????|????| + |????????????|???????????? =0.
?
【点拨】对于任意非零有理数 m :当 m >0时,| m |=
m , |????|???? = ???????? =1;当 m <0时,| m |=- m , |????|???? =
????????? =-1.
?
已知非零有理数 a , b , c 满足 ab >0, bc >0.
(1)求 |????????|???????? + ????????|????????| + |????????|???????? 的值;
?
(1) |????????|???????? + ????????|????????| + |????????|???????? =1+1+1=3.
?
解:因为 ab >0, bc >0,
所以 a , b , c 同号,则 ac >0.
(2)若 a + b + c <0,试求 |????|???? + ????|????| + ????|????| +
|????????????|???????????? 的值.
?
解:(2)因为 a + b + c <0,且 a , b , c 同号,
所以 a , b , c , abc 均为负数.
所以 |????|???? + ????|????| + ????|????| + |????????????|????????????
=(-1)+(-1)+(-1)+(-1)
=-4.
第二章 有理数及其运算
2.4 有理数的乘除运算
1.理解有理数除法法则,体会除法与乘法的联系。
2.会利用有理数除法法则进行有理数的除法运算。
学习目标
情境导入
除法与乘法是互逆运算,在小学我们就认识到除法与乘法相互转化可以简化运算,那么在有理数范围内,又怎样将除法转化成乘法?有理数的除法可以怎样进行计算呢?
(-12)÷(-3)=?你能得出结果吗?
被除数=除数×商
那么:-12=(-3 ) × ?
我们知道只有:(-3)× 4 =-12
所以(-12)÷(-3)=4
知识点1
教学过程
在小学我们就已经知道,乘法与除法互为逆运算,为了计算(?????????)÷4,我们必须找到一个数与????相乘等于?????????.
?
因为(?????)×????=?????????, 所以(?????????)÷????=?????
?
.
有理数除法法则(1)
知识点1
教学过程
有理数除法法则(1)
利用乘法与除法互为逆运算,计算下面各题:
(1) (?????????)÷(?????), (????) (?????????)÷(?????),
(????) (?????????)÷????, (????) ????????÷(?????????) ,
(????) ????÷???????? , (????) ????÷(?????????)。
?
.
知识点1
教学过程
利用乘法与除法互为逆运算,计算下面各题:
.
想一想:两个有理数相除,商的符号与除数和被除数的符号有什么关系?
(1) (?????????)÷(?????)=????;
?
.
(????) (?????????)÷(?????)=????;
?
.
(????) (?????????)÷????=?????;
?
.
(????) ????????÷(?????????)=????? ;
?
.
(????) ????÷????????=???? ;
?
.
(????) ????÷(?????????)=???? ;
?
.
有理数除法法则(1)
知识点1
教学过程
由此我们得到有理数除法法则:
.
有理数除法法则(1)
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何数都是得0。
注意:0不能作除数。
?
有理数除法法则(1)
学以致用
教学过程
计算:
.
.
.
(1) (?????????????)÷(?????????), (????) ????????÷(?????????),
?
.
新课讲授
除以一个不等于0的数,等于乘这个数的倒数.
a ÷ b = a · (b≠0)
除号变乘号
除数变为它的倒数
符号语言:
有理数的除法法则二:
知识归纳
新课讲授
2.计算:(1)(-18)÷(?????????); (????)????????÷(?????????)÷(?????????????).
?
解:(1)原式= (-18)×(?????????)
=18×????????
=27;
?
(2)原式= 16×(?????????)×(?????????????)
=16×(?????????????)×(?????????)
=????????????.
?
新课讲授
方法归纳
有理数除法运算的方法:
1.对于只有除法的运算,有括号先算括号内,无括号就从左到右运算;
2.可以先把所有除法都变成乘法,然后再用乘法交换律和结合律.
新课讲授
思考·交流:
(1)将除法转化为乘法有什么好处?
将除法转化为乘法的主要好处包括简化计算过程、节约时间、提高计算效率;
相同点:都是整数与分数的运算,大部分知识是在小学就学过了.
不同点:初中有理数运算新增了一些乘法公式,并且运算起来比小学的复杂,有时还会用字母表示数,用复杂的代数式运算.
(2)有理数的乘除法与小学数学中的乘除法相比较,有哪些相同点和不同点?与同伴进行交流。
5.【阅读材料】定义:如果两个有理数的差等于这两个有理数的商,那么这两个有理数就叫作“差商等数对”.即:如果a-b=a÷b,那么a与b就叫作“差商等数对”,记为(a,b).例如:4-2=4÷2,????????-3=????????÷3,则称数对(4,2),????????,????是“差商等数对”.
【动手解决】下列数对中,是“差商等数对”的是 .(选填序号)?
①????????,?????; ②????????????,????.
?
②
1.21÷(-7)的结果是( )
A.3 B.-3 C.???????? D.-????????
2.与-2的乘积为1的数是( )
A.2 B.-2 C.???????? D.-????????
?
B
D
3.与2÷3÷4运算结果相同的是( )
A.2÷(3÷4) B.2÷(3×4)
C.2÷(4÷3) D.3÷2÷4
4.计算:(1)(-8)÷?????????= ;?
(2)(-1)÷(-6)÷?????????= .?
?
B
32
-1
5.小明星期天到体育用品商店购买一个排球花了36元.已知排球按标价打八折,那么排球的标价是 元.?
45
6.计算:
(1)(-5)÷?????????????×????????×?????????????÷7; (2)?????????????????+????????÷????????????.
?
(1)-????????.
?
(2)1.
随 堂 训 练
1.计算 的结果正确的是 ( )
C
C
2.计算-15÷(-5)的结果正确的是( )
A.75 B.-75 C.3 D.-3
4.算式 中的括号内应填上 ( )
D
?
A
随堂训练
1. 规定一种新的运算:A★B=A×B-A÷B,如4★2=4×2-4÷2=6,则6★(-3)的值为 .
-16
课后提升
?
?
D
B
A
B
有理数的除法法则:
有理数除法的计算方法:
有理数的除法
同号得正,异号得负,并把绝对值相除;
0 除以任何一个非 0 的数都得 0.
除以一个数,等于乘这个数的倒数.
整数的除法,先确定符号,并把两数的绝对值相除.
有分数或小数参与的运算,将除法转化为乘法,确定结果符号后再计算,一般情况下会比较简便.
已知非零有理数 a , b , c 满足 a + b + c =0,试求 |????|???? +
????|????| + ????|????| + |????????????|???????????? 的值.
?
【思路导航】因为 a , b , c 非零且和为0,所以 a , b , c 中有
两正一负或两负一正,所以可分情况得到 |????|???? , ????|????| ,
????|????| , |????????????|???????????? 中有几个-1和1,从而求出 |????|???? + ????|????| +
????|????| + |????????????|???????????? 的值.
?
解:因为 a , b , c 为非零有理数,且 a + b + c =0,
所以 a , b , c 中有两正一负或两负一正.
①当 a , b , c 中有两正一负时, abc <0,则 |????????????|???????????? =-1,
|????|???? , ????|????| , ????|????| 中有两个等于1,一个等于-1,
故 |????|???? + ????|????| + ????|????| + |????????????|???????????? =0;
?
②当 a , b , c 中有两负一正时, abc >0,则 |????????????|???????????? =1,
|????|???? , ????|????| , ????|????| 中有一个等于1,两个等于-1,
故 |????|???? + ????|????| + ????|????| + |????????????|???????????? =0.
综上所述, |????|???? + ????|????| + ????|????| + |????????????|???????????? =0.
?
【点拨】对于任意非零有理数 m :当 m >0时,| m |=
m , |????|???? = ???????? =1;当 m <0时,| m |=- m , |????|???? =
????????? =-1.
?
已知非零有理数 a , b , c 满足 ab >0, bc >0.
(1)求 |????????|???????? + ????????|????????| + |????????|???????? 的值;
?
(1) |????????|???????? + ????????|????????| + |????????|???????? =1+1+1=3.
?
解:因为 ab >0, bc >0,
所以 a , b , c 同号,则 ac >0.
(2)若 a + b + c <0,试求 |????|???? + ????|????| + ????|????| +
|????????????|???????????? 的值.
?
解:(2)因为 a + b + c <0,且 a , b , c 同号,
所以 a , b , c , abc 均为负数.
所以 |????|???? + ????|????| + ????|????| + |????????????|????????????
=(-1)+(-1)+(-1)+(-1)
=-4.
同课章节目录
