2.4有理数的乘除运算 第2课时 课件(共26张PPT) 2024-2025学年鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.4有理数的乘除运算 第2课时 课件(共26张PPT) 2024-2025学年鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 17:23:35 | ||
图片预览








文档简介
(共26张PPT)
2.4.有理数的乘法(第2课时)
第二章 有理数及其运算
学习目标
1.探讨有理数乘法的运算律并会用字母表示.
2.熟练地运用乘法的运算律进行运算.
课堂导入
问题
小学我们都学了哪些乘法定律?
乘法交换律
乘法结合律
乘法对加法
的分配律
两个数相乘,交换乘数的位置,积不变.
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
新知探究
思考1:引入负数后,这些运算律是否还成立呢
知识点 有理数乘法运算律
新知探究
用计算器计算下列各题:
( 7)×8 8×( 7)
= 56
你能得到什么结论?
乘法的交换律可延伸至有理数
= 56
知识点 有理数乘法运算律
导入新课
1. 有理数的乘法法则:
2. 小学学过乘法的哪些运算律:
两数相乘,同号得正,
任何数与 0 相乘,积仍为 0。
异号得负,并把绝对值相乘。
乘法交换律、结合律和分配律。
自主探究
例1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
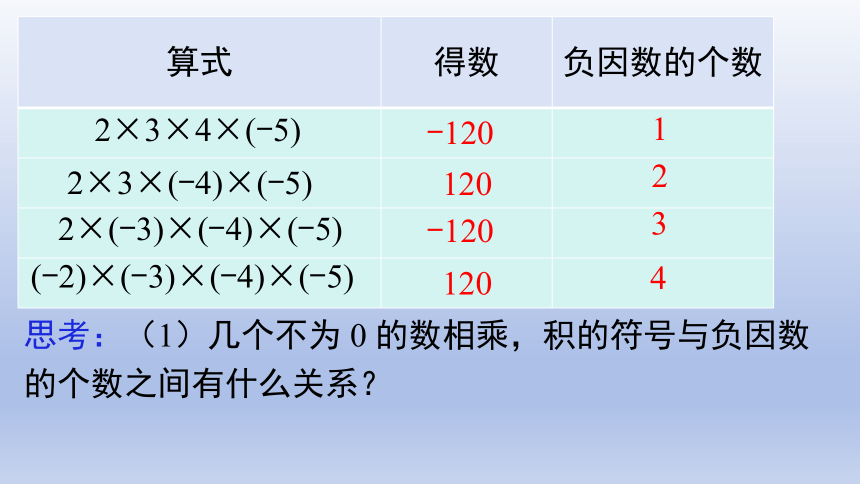
算式 得数 负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
典例分析
解:(1)原式=[(-2.5)×(-4)]×[8×(-0.125)]×(-0.1)
=10×(-1)×(-0.1)
=1.
典例分析
方法一:
方法二:
逆用乘法对加法的分配律.
例2 计算:
典例分析
方法一:
方法二:
=-699×2
学以致用
1.n个不等于0的有理数相乘,它们的符号( ).
A.由因数的个数而定 B.由正因数的个数而定
C.由负因数的个数而定 D.由负因数的大小而定
C
2.计算 的值为 ( )
D
学以致用
4.算式-25×14+18×14-39×(-14)=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法对加法的分配律
D
3.下列计算正确的是( )
A.-5×(-4)×(-2)×(-3)=5×4×2×3=120
B.(-9)×5×(-4)×0=9×5×4=180
C.(-3)×(-9)-8×(-5)=27-40=-13
=7×
=
D.7×
A
知识点:有理数乘法的简便运算
1.计算×(-2)+×(-2)的结果是( )
A.-2 B.0 C.1 D.2
2.计算:(1)(-6)×= ; (2)25×(-26)×(-4)= .
A
5
2 600
3.用简便方法计算:
(1)30×; (2)100×(-3)×(-5)×0.01; (3)25××(-4)×.
(1)5.
(2)15.
(3)100.
4.学习了有理数的乘法运算后,老师给同学们出了一题.计算:19×(-9).
下面是两位同学的解法:
小方:原式=-×9=-=-179.
小杨:原式=×(-9)=-19×9-×9=-179.
(1)两位同学的解法中,谁的解法较好
(2)请你写出另一种更好的解法.
解:(1)小杨的解法较好.
(2)19×(-9)=×(-9)
=20×(-9)-×(-9)
=-180+
=-179.
1.已知=2,=1,且xy<0,则x+y=( )
A.3 B.3或-3
C. 1或-1 D.1
2.计算:
(1)(-2)×(-18)+(-5)= ;
(2)30×= .
C
31
7
3.用简便方法计算:
(1)×(-12); (2)5×+17×-12×.
(1)1.
(2)-.
【变式训练】
用乘法运算律简便计算:
(1)×(-)×(-2)×(-4);
(2) (-)×+(-)×.
【解析】(1)×(-)×(-2)×(-4)
=[×(-) ]×[(-)×(-) ]=-×1
=-;
(2) (-)×+(-)×=(-)×(+)=(-)×2=-.
【能力练】
4.(2024·湛江徐闻期末)计算743×369-741×370的结果是( )
A.-3 B.-2 C.2 D.3
【解析】原式=743×(370-1)-741×370
=370×(743-741)-743
=370×2-743=-3.
5.计算:78×(-)+(-11)×(-)+(-33)×=________.
【解析】78×(-)+(-11)×(-)+(-33)×=78×(-)+(-11)×(-)+33×(-)=-×(78-11+33)
=-×100=-60.
A
-60
【培优练】
6.(运算能力)阅读材料,回答问题.
×=×=1,
×××=
×××=×=1×1=1.
根据以上信息,请求出下式的结果.
×××…×(1+)××××…×(1-).
【解析】(1+)×(1+)×(1+)×…×(1+)×(1-)×(1-)×(1-)×…×(1-)=×××…×××××…×=(×)×(×)×(×)×…×(×)=
1×1×1×…×1=1.
谢 谢
2.4.有理数的乘法(第2课时)
第二章 有理数及其运算
学习目标
1.探讨有理数乘法的运算律并会用字母表示.
2.熟练地运用乘法的运算律进行运算.
课堂导入
问题
小学我们都学了哪些乘法定律?
乘法交换律
乘法结合律
乘法对加法
的分配律
两个数相乘,交换乘数的位置,积不变.
三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变.
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.
新知探究
思考1:引入负数后,这些运算律是否还成立呢
知识点 有理数乘法运算律
新知探究
用计算器计算下列各题:
( 7)×8 8×( 7)
= 56
你能得到什么结论?
乘法的交换律可延伸至有理数
= 56
知识点 有理数乘法运算律
导入新课
1. 有理数的乘法法则:
2. 小学学过乘法的哪些运算律:
两数相乘,同号得正,
任何数与 0 相乘,积仍为 0。
异号得负,并把绝对值相乘。
乘法交换律、结合律和分配律。
自主探究
例1:观察下列各式,它们的积是正的还是负的?
2×3×4×(-5);
2×3×(-4)×(-5);
2×(-3)×(-4)×(-5);
(-2)×(-3)×(-4)×(-5);
算式 得数 负因数的个数
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
-120
1
120
2
-120
3
120
4
思考:(1)几个不为 0 的数相乘,积的符号与负因数的个数之间有什么关系?
归纳总结
几个不是 0 的数相乘,
负因数的个数是_____时,积为正;
负因数的个数是_____时,积为负。
奇数
偶数
奇负偶正
典例精析
例2 计算:
①先确定积的符号
②再确定积的绝对值
解:(1) 原式 ;
(2) 原式 。
。
典例分析
解:(1)原式=[(-2.5)×(-4)]×[8×(-0.125)]×(-0.1)
=10×(-1)×(-0.1)
=1.
典例分析
方法一:
方法二:
逆用乘法对加法的分配律.
例2 计算:
典例分析
方法一:
方法二:
=-699×2
学以致用
1.n个不等于0的有理数相乘,它们的符号( ).
A.由因数的个数而定 B.由正因数的个数而定
C.由负因数的个数而定 D.由负因数的大小而定
C
2.计算 的值为 ( )
D
学以致用
4.算式-25×14+18×14-39×(-14)=(-25+18+39)×14是逆用了( )
A.加法交换律 B.乘法交换律
C.乘法结合律 D.乘法对加法的分配律
D
3.下列计算正确的是( )
A.-5×(-4)×(-2)×(-3)=5×4×2×3=120
B.(-9)×5×(-4)×0=9×5×4=180
C.(-3)×(-9)-8×(-5)=27-40=-13
=7×
=
D.7×
A
知识点:有理数乘法的简便运算
1.计算×(-2)+×(-2)的结果是( )
A.-2 B.0 C.1 D.2
2.计算:(1)(-6)×= ; (2)25×(-26)×(-4)= .
A
5
2 600
3.用简便方法计算:
(1)30×; (2)100×(-3)×(-5)×0.01; (3)25××(-4)×.
(1)5.
(2)15.
(3)100.
4.学习了有理数的乘法运算后,老师给同学们出了一题.计算:19×(-9).
下面是两位同学的解法:
小方:原式=-×9=-=-179.
小杨:原式=×(-9)=-19×9-×9=-179.
(1)两位同学的解法中,谁的解法较好
(2)请你写出另一种更好的解法.
解:(1)小杨的解法较好.
(2)19×(-9)=×(-9)
=20×(-9)-×(-9)
=-180+
=-179.
1.已知=2,=1,且xy<0,则x+y=( )
A.3 B.3或-3
C. 1或-1 D.1
2.计算:
(1)(-2)×(-18)+(-5)= ;
(2)30×= .
C
31
7
3.用简便方法计算:
(1)×(-12); (2)5×+17×-12×.
(1)1.
(2)-.
【变式训练】
用乘法运算律简便计算:
(1)×(-)×(-2)×(-4);
(2) (-)×+(-)×.
【解析】(1)×(-)×(-2)×(-4)
=[×(-) ]×[(-)×(-) ]=-×1
=-;
(2) (-)×+(-)×=(-)×(+)=(-)×2=-.
【能力练】
4.(2024·湛江徐闻期末)计算743×369-741×370的结果是( )
A.-3 B.-2 C.2 D.3
【解析】原式=743×(370-1)-741×370
=370×(743-741)-743
=370×2-743=-3.
5.计算:78×(-)+(-11)×(-)+(-33)×=________.
【解析】78×(-)+(-11)×(-)+(-33)×=78×(-)+(-11)×(-)+33×(-)=-×(78-11+33)
=-×100=-60.
A
-60
【培优练】
6.(运算能力)阅读材料,回答问题.
×=×=1,
×××=
×××=×=1×1=1.
根据以上信息,请求出下式的结果.
×××…×(1+)××××…×(1-).
【解析】(1+)×(1+)×(1+)×…×(1+)×(1-)×(1-)×(1-)×…×(1-)=×××…×××××…×=(×)×(×)×(×)×…×(×)=
1×1×1×…×1=1.
谢 谢
同课章节目录
