2.2 第4课时 有理数的加减混合运算 课件(共23张PPT) 2024-2025学年 鲁教版五四制六年级上册数学
文档属性
| 名称 | 2.2 第4课时 有理数的加减混合运算 课件(共23张PPT) 2024-2025学年 鲁教版五四制六年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 17:40:41 | ||
图片预览








文档简介
(共23张PPT)
第二章 有理数及其运算
2.3 有理数的加减运算
第4课时 有理数的加减混合运算
第二章 有理数及其运算
1
2
能熟练地进行有理数的加减混合运算,理解加减法统一成加法的意义。(重点)
学习目标
适当应用加法运算律简化运算,提高运算能力。(难点)
1.有理数加法法则:
2.有理数减法法则:
减一个数,等于加这个数的相反数。即 )。
加法的交换律:
加法的结合律:
3.运算律:
(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
(3)一个数同0相加,仍得这个数。
知识回顾
新知初探
探究一 有理数的加减混合运算
贰
1.引入相反数后,加减混合运算可以统一为加法运算。
如:a+b-c=a+b+______
2.将上面的算式转化为加法:____________________________。
3.这个算式我们可以看作是___、___、___、___这四个数的和。
4.为书写简单,省略算式中的括号和加号写为___________。
5.我们可以读作_________________________的和,或读作
_____加____加____减____。
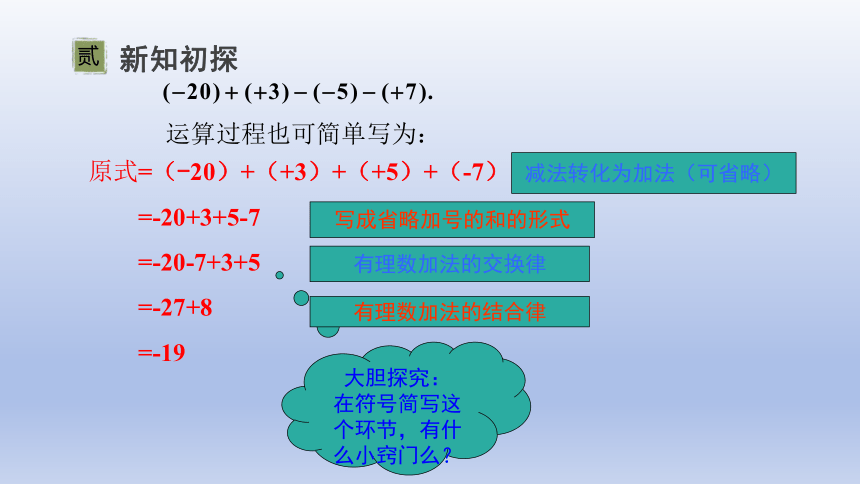
(-20)+(+3)-(-5)-(+7)
(-c)
-20+3+5-7
负20、正3 、正5、负7
(-20)+(+3)+(+5)+(-7)
-20 3 5 -7
负20 3 5 7
合作探究
新知初探
贰
大胆探究:
在符号简写这个环节,有什么小窍门么?
原式=(-20)+(+3)+(+5)+(-7)
=-20+3+5-7
=-20-7+3+5
=-27+8
=-19
减法转化为加法(可省略)
写成省略加号的和的形式
有理数加法的交换律
有理数加法的结合律
运算过程也可简单写为:
新知初探
贰
例题 计算:
(1) ;(2)
解:原式=
解:原式=
新知初探
贰
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算。
归纳总结
新知初探
贰
试一试:把下列各式写成省略加号的形式,并说出它们的两种读法。
(-6)-(-3)+(-2)-(+6)-(-7);
解:(-6)-(-3)+(-2)-(+6)-(-7)
=(-6)+(+3)+(-2)+(-6)+(+7)
=-6+3-2-6+7.
读法一:负6,正3,负2,负6,正7的和;
读法二:负6加3减2减6加7。
知识点2
教学过程
有理数混合运算的运算顺序
.
小红和小米进行抽牌游戏,规定每人从不同颜色的卡片中任意抽取4张,抽到白色卡片就加上卡片上数字,抽到红色卡片就减去卡片上的数字,谁先算结果大的获胜
小红抽到的
小米抽到的
帮她们算一算
15
知识点2
教学过程
有理数混合运算的运算顺序
.
15
小红抽到的
=7-11+15
=-4+15
=11
.
想一想:有理数
的加减混合运算顺序是怎样的?
知识点2
教学过程
有理数混合运算的运算顺序
.
小米抽到的
=12+(+)+(-)+(-)
=
=
=12
.
有理数的加减混合运算先统一成加法运算,再写成省略加号的和的形式,最后合理应用有理数加法的运算律,使计算简便.
典例解析
教学过程
.
例. 计算:
(1)
.
(2)
.
(4)
.
(3)
.
方法总结
教学过程
有理数加减混合运算步骤:
.
1. 将加减混合运算统一成加法运算;
.
2. 写成省略加号和括号的和的形式;
.
3. 综合应用运算律进行运算.
.
【对点小练】
计算-7-(-5)+(-4)-(-10)的结果为( )
A.26 B.-26 C.4 D.-4
C
【典例微课】
【重点1】有理数的加减混合运算(运算能力)
【典例1】(教材再开发·P40例5补充)计算:
(1)-0.9+8.7-5.6-7.2;
(2)(-7.7)- (-4)+(-2)+5.75.
【完善解答】
(1)-0.9+8.7-5.6-7.2
=-0.9+8.7+_____+_____(化减为加)
=8.7+[(-0.9)+_____+_____](加法运算律)
=8.7+______(加法运算)
=___.(加法运算)
(2)(-7.7)- (-4)+(-2)+5.75
=-7.7+___+(-2)+5.75(化减为加)
=-7.7+_______+______ (加法运算律)
=____+___(加法运算)
=__.(加法运算)
(-5.6)
(-7.2)
(-5.6)
(-7.2)
(-13.7)
-5
4
-10
10
0
【变式训练】
1.把1-2-(-4)-3统一为加法运算,正确的是( )
A.(+1)+(+2)+(-4)+(-3)
B.(+1)+(-2)+(+4)+(-3)
C.(+1)+(+2)+(+4)+(+3)
D.(+1)+(-2)+(-4)+(+3)
【解析】原式=(+1)+(-2)+(+4)+(-3).
B
2.计算(+)-(-2)+ (+1)的结果是( )
A.0 B.4 C.2 D.-2
【解析】原式=+2+1=(+1)+2=2+2=4.
B
9. 规定图形 表示运算 a - b + c ,图形 表示运算 x + z
- y - w ,则 + = (直接写出答案).
10. 已知| a |=1,| b |=2,| c |=3,且 a > b > c ,则 a
+ b - c = .
0
0或2
【解析】因为| a |=1,| b |=2,| c |=3,
所以 a =±1, b =±2, c =±3.
又因为 a > b > c ,
所以 b =-2, c =-3.
①当 a =1时, a + b - c =1+(-2)-(-3)=2;
②当 a =-1时, a + b - c =-1+(-2)-(-3)=0.
故答案为0或2.
11. 体育课上,七年级(1)班女生进行了一分钟跳绳测验,达
标成绩为140个.下面是第一组8名女生的成绩记录,其中“+”
表示超过达标成绩,“-”表示不足达标成绩.-25,+17,+
23,0,-39,-11,+9,+34.
(1)这8名女生中最好成绩与最差成绩相差 个;
73
(1)【解析】34-(-39)=34+39=73(个).
故这8名女生中最好成绩与最差成绩相差73个.故答案为73.
(2)这8名女生的平均成绩为多少个?
(2)解:140+(-25+17+23+0-39-11+9+34)÷8=
140+8÷8=140+1=141(个).
故这8名女生的平均成绩为141个.
(3)规定:一分钟跳绳个数为达标成绩,不得分;超过达标成
绩,每多跳1个得2分;未达到达标成绩,每少跳1个扣1分.若全
组8名女生一分钟跳绳个数总得分超过100分,便可得到运动达
人小组称号,请通过计算说明第一组8名女生能否获得该称号.
(3)解:(17+23+9+34)×2-(25+39+11)×1=91
(分).
因为91<100,
所以第一组8名女生不能获得该称号.
第二章 有理数及其运算
2.3 有理数的加减运算
第4课时 有理数的加减混合运算
第二章 有理数及其运算
1
2
能熟练地进行有理数的加减混合运算,理解加减法统一成加法的意义。(重点)
学习目标
适当应用加法运算律简化运算,提高运算能力。(难点)
1.有理数加法法则:
2.有理数减法法则:
减一个数,等于加这个数的相反数。即 )。
加法的交换律:
加法的结合律:
3.运算律:
(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
(3)一个数同0相加,仍得这个数。
知识回顾
新知初探
探究一 有理数的加减混合运算
贰
1.引入相反数后,加减混合运算可以统一为加法运算。
如:a+b-c=a+b+______
2.将上面的算式转化为加法:____________________________。
3.这个算式我们可以看作是___、___、___、___这四个数的和。
4.为书写简单,省略算式中的括号和加号写为___________。
5.我们可以读作_________________________的和,或读作
_____加____加____减____。
(-20)+(+3)-(-5)-(+7)
(-c)
-20+3+5-7
负20、正3 、正5、负7
(-20)+(+3)+(+5)+(-7)
-20 3 5 -7
负20 3 5 7
合作探究
新知初探
贰
大胆探究:
在符号简写这个环节,有什么小窍门么?
原式=(-20)+(+3)+(+5)+(-7)
=-20+3+5-7
=-20-7+3+5
=-27+8
=-19
减法转化为加法(可省略)
写成省略加号的和的形式
有理数加法的交换律
有理数加法的结合律
运算过程也可简单写为:
新知初探
贰
例题 计算:
(1) ;(2)
解:原式=
解:原式=
新知初探
贰
有理数加减混合运算的步骤:
(1)将减法转化为加法运算;
(2)省略加号和括号;
(3)运用加法交换律和结合律,将同号两数相加;
(4)按有理数加法法则计算。
归纳总结
新知初探
贰
试一试:把下列各式写成省略加号的形式,并说出它们的两种读法。
(-6)-(-3)+(-2)-(+6)-(-7);
解:(-6)-(-3)+(-2)-(+6)-(-7)
=(-6)+(+3)+(-2)+(-6)+(+7)
=-6+3-2-6+7.
读法一:负6,正3,负2,负6,正7的和;
读法二:负6加3减2减6加7。
知识点2
教学过程
有理数混合运算的运算顺序
.
小红和小米进行抽牌游戏,规定每人从不同颜色的卡片中任意抽取4张,抽到白色卡片就加上卡片上数字,抽到红色卡片就减去卡片上的数字,谁先算结果大的获胜
小红抽到的
小米抽到的
帮她们算一算
15
知识点2
教学过程
有理数混合运算的运算顺序
.
15
小红抽到的
=7-11+15
=-4+15
=11
.
想一想:有理数
的加减混合运算顺序是怎样的?
知识点2
教学过程
有理数混合运算的运算顺序
.
小米抽到的
=12+(+)+(-)+(-)
=
=
=12
.
有理数的加减混合运算先统一成加法运算,再写成省略加号的和的形式,最后合理应用有理数加法的运算律,使计算简便.
典例解析
教学过程
.
例. 计算:
(1)
.
(2)
.
(4)
.
(3)
.
方法总结
教学过程
有理数加减混合运算步骤:
.
1. 将加减混合运算统一成加法运算;
.
2. 写成省略加号和括号的和的形式;
.
3. 综合应用运算律进行运算.
.
【对点小练】
计算-7-(-5)+(-4)-(-10)的结果为( )
A.26 B.-26 C.4 D.-4
C
【典例微课】
【重点1】有理数的加减混合运算(运算能力)
【典例1】(教材再开发·P40例5补充)计算:
(1)-0.9+8.7-5.6-7.2;
(2)(-7.7)- (-4)+(-2)+5.75.
【完善解答】
(1)-0.9+8.7-5.6-7.2
=-0.9+8.7+_____+_____(化减为加)
=8.7+[(-0.9)+_____+_____](加法运算律)
=8.7+______(加法运算)
=___.(加法运算)
(2)(-7.7)- (-4)+(-2)+5.75
=-7.7+___+(-2)+5.75(化减为加)
=-7.7+_______+______ (加法运算律)
=____+___(加法运算)
=__.(加法运算)
(-5.6)
(-7.2)
(-5.6)
(-7.2)
(-13.7)
-5
4
-10
10
0
【变式训练】
1.把1-2-(-4)-3统一为加法运算,正确的是( )
A.(+1)+(+2)+(-4)+(-3)
B.(+1)+(-2)+(+4)+(-3)
C.(+1)+(+2)+(+4)+(+3)
D.(+1)+(-2)+(-4)+(+3)
【解析】原式=(+1)+(-2)+(+4)+(-3).
B
2.计算(+)-(-2)+ (+1)的结果是( )
A.0 B.4 C.2 D.-2
【解析】原式=+2+1=(+1)+2=2+2=4.
B
9. 规定图形 表示运算 a - b + c ,图形 表示运算 x + z
- y - w ,则 + = (直接写出答案).
10. 已知| a |=1,| b |=2,| c |=3,且 a > b > c ,则 a
+ b - c = .
0
0或2
【解析】因为| a |=1,| b |=2,| c |=3,
所以 a =±1, b =±2, c =±3.
又因为 a > b > c ,
所以 b =-2, c =-3.
①当 a =1时, a + b - c =1+(-2)-(-3)=2;
②当 a =-1时, a + b - c =-1+(-2)-(-3)=0.
故答案为0或2.
11. 体育课上,七年级(1)班女生进行了一分钟跳绳测验,达
标成绩为140个.下面是第一组8名女生的成绩记录,其中“+”
表示超过达标成绩,“-”表示不足达标成绩.-25,+17,+
23,0,-39,-11,+9,+34.
(1)这8名女生中最好成绩与最差成绩相差 个;
73
(1)【解析】34-(-39)=34+39=73(个).
故这8名女生中最好成绩与最差成绩相差73个.故答案为73.
(2)这8名女生的平均成绩为多少个?
(2)解:140+(-25+17+23+0-39-11+9+34)÷8=
140+8÷8=140+1=141(个).
故这8名女生的平均成绩为141个.
(3)规定:一分钟跳绳个数为达标成绩,不得分;超过达标成
绩,每多跳1个得2分;未达到达标成绩,每少跳1个扣1分.若全
组8名女生一分钟跳绳个数总得分超过100分,便可得到运动达
人小组称号,请通过计算说明第一组8名女生能否获得该称号.
(3)解:(17+23+9+34)×2-(25+39+11)×1=91
(分).
因为91<100,
所以第一组8名女生不能获得该称号.
同课章节目录
