2024-2025学年上海华二附中高三数学冲刺4(含答案)
文档属性
| 名称 | 2024-2025学年上海华二附中高三数学冲刺4(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 23:34:02 | ||
图片预览




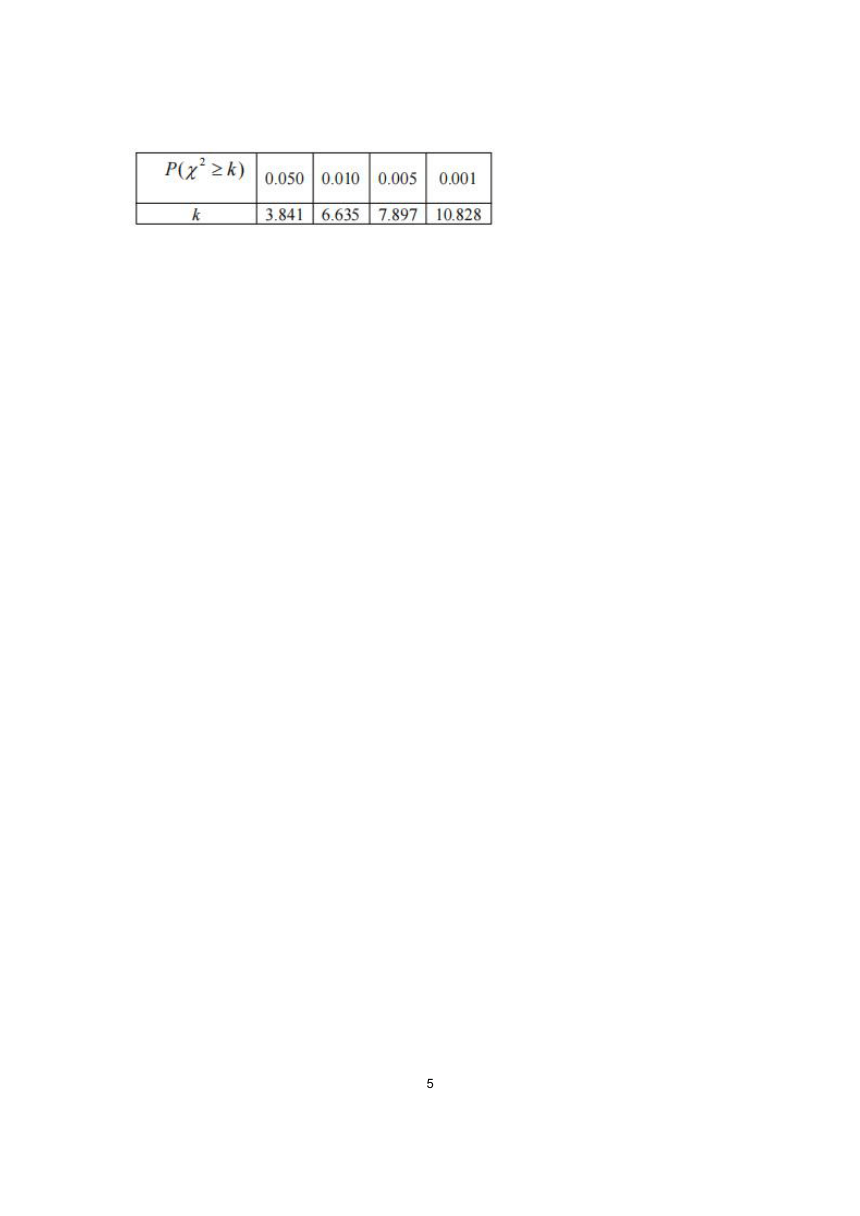
文档简介
华二2024-2025学年第二学期高三年级数学冲刺卷4
2025.5
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的值域为 .
2.设i是虚数单位,则 .
3.一组统计数据为,则该组数据的第85百分位数是 .
4.不等式的解集为 .
5.椭圆的焦距为 .
6.已知向量,则 .
7.若二项式的展开式中存在常数项,则正整数的最小值为 .
8.在中,边依次成等比数列,则内角的最大值为 .
9.从5个函数中随机选出两个函数,记选出的两个函数中,图像经过第二象限的函数的个数为,则的数学期望为 .
10.在平面直角坐标系中,已知点,点在抛物线上,若,则点横坐标的取值范围为 .
11.某生产线有一批边长相等的正方形铁皮,用每一块铁皮都可以加工出一个无盖的正四棱锥容器.具体的加工方式为:裁下图1中的阴影部分,余下的四个全等的等腰三角形作为容器的侧面(如图2).现要求每个容器的容积要达到最大,则在裁剪铁皮时应保证余下的等腰三角形的底角大小为 .
(第11题图1) (第11题图2)
12.设集合由所有满足下列条件的有序数组构成:①每一个元素等于中之一;②,则中元素个数为 .
二、选择题(本大题共有4题,满分18分,13-14每题4分,15-16每题5分).
13.已知集合满足,则( ).
A.P B.N C.M D.
14.在四面体中,分别是的重心,则与平面平行的棱有( ).
A.0条 B.1条 C.2条 D.3条
15.已知数列是正项等差数列,前项和为,则( ).
A.数列一定是等比数列 B.数列一定是等比数列
C.数列一定是等差数列 D.数列一定是等差数列
16.已知函数的定义域为[],对定义域内任意的的取值为或.有如下两个命题:
①若有且仅有2025个实数使得关于的方程只有1个解,则函数至少存在2025个严格减区间;
②若对任意满足条件的函数,方程都有解,则实数存在8101个可能的取值;则( ).
A.①正确; ②正确 B.①正确;②错误
C.①错误;②正确 D.①错误;②错误
三、解答题(本大题共5题,满分78分).
17.(本题满分14分,共有2个小题,第1小题满分6分,第2小题满分8分.)
已知函数的两个相邻极值点为和.
(1)求函数的解析式;
(2)设是锐角的内角,,求的取值范围.
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,直四棱柱的底面是边长为2的菱形,,侧面积为.点为和的交点,点是棱上一个动点,且不与顶点重合.
(1)当时,求的值;
(2)若锐二面角的余弦值为,求的值.
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
为促进国民身体健康,国家卫生健康委员会2025年在新闻发布会上提出将开展为期3年的"体重管理年"活动.某校为了解高一同学的体重情况,从高一年级随机抽取了66名学生,统计了他们的体重(单位:千克),并绘制了如下的茎叶图:
(1)为了解学生"体重低于75千克"是否与学生"性别"有关,将上述数据绘制成如下的列联表:
①将列联表补充完整;
②是否有的把握认为学生"体重低于75千克"与学生"性别"有关,说明理由;
(2)现从该校高一年级随机抽取200名学生,用(1)中的频率估计概率,则体重不少于75千克的学生最有可能有多少名?附:,
20.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知双曲线的右焦点分别为,直线与双曲线的左右支分别交于两点,且.
(1)当时,求双曲线的离心率;
(2)当时,求的面积;
(3)当时,求证:以和为邻边的矩形周长大于.
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数存在极值,并且其导函数的极值点是的零点,则称函数具有性质.
(1)判断函数和是否具有性质,并说明理由;
(2)设函数,求证:函数不具有性质;
(3)若函数具有性质,记函数和的所有极值之和为,求证:""是""的充分非必要条件.
华二2024-2025学年第二学期高三年级数学冲刺卷4
2025.5
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的值域为 .
【答案】
2.设i是虚数单位,则 .
【答案】1
3.一组统计数据为,则该组数据的第85百分位数是 .
【答案】99
4.不等式的解集为 .
【答案】
5.椭圆的焦距为 .
【答案】4
6.已知向量,则 .
【答案】
7.若二项式的展开式中存在常数项,则正整数的最小值为 .
【答案】11
8.在中,边依次成等比数列,则内角的最大值为 .
【答案】
9.从5个函数中随机选出两个函数,记选出的两个函数中,图像经过第二象限的函数的个数为,则的数学期望为 .
【答案】
10.在平面直角坐标系中,已知点,点在抛物线上,若,则点横坐标的取值范围为 .
【答案】
11.某生产线有一批边长相等的正方形铁皮,用每一块铁皮都可以加工出一个无盖的正四棱锥容器.具体的加工方式为:裁下图1中的阴影部分,余下的四个全等的等腰三角形作为容器的侧面(如图2).现要求每个容器的容积要达到最大,则在裁剪铁皮时应保证余下的等腰三角形的底角大小为 .
(第11题图1) (第11题图2)
【答案】
12.设集合由所有满足下列条件的有序数组构成:①每一个元素等于中之一;②,则中元素个数为 .
【答案】169
二、选择题(本大题共有4题,满分18分,13-14每题4分,15-16每题5分).
13.已知集合满足,则( ).
A.P B.N C.M D.
【答案】A
14.在四面体中,分别是的重心,则与平面平行的棱有( ).
A.0条 B.1条 C.2条 D.3条
【答案】B
15.已知数列是正项等差数列,前项和为,则( ).
A.数列一定是等比数列 B.数列一定是等比数列
C.数列一定是等差数列 D.数列一定是等差数列
【答案】
16.已知函数的定义域为[],对定义域内任意的的取值为或.有如下两个命题:
①若有且仅有2025个实数使得关于的方程只有1个解,则函数至少存在2025个严格减区间;
②若对任意满足条件的函数,方程都有解,则实数存在8101个可能的取值;则( ).
A.①正确; ②正确 B.①正确;②错误
C.①错误;②正确 D.①错误;②错误
【答案】
三、解答题(本大题共5题,满分78分).
17.(本题满分14分,共有2个小题,第1小题满分6分,第2小题满分8分.)
已知函数的两个相邻极值点为和.
(1)求函数的解析式;
(2)设是锐角的内角,,求的取值范围.
【答案】(1) (2)
【解析】(1)由题意,即,
即
(2)
且
即
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,直四棱柱的底面是边长为2的菱形,,侧面积为.点为和的交点,点是棱上一个动点,且不与顶点重合.
(1)当时,求的值;
(2)若锐二面角的余弦值为,求的值.
【答案】(1) (2)或
【解析】(1)棱柱高,在菱形中,
以为原点,所在直线为轴建立空间直角坐标系(如图).则,设长为,则,
∴,即.
(2),
设平面的法向量为,则,
即,令,则
∵,设平面的法向量为,
则即令,则
设锐二面角的平面角为,则,
解得或或.
【解法2】(1)运用三垂线定理;(2)借助二面角平面角的定理,利用余弦定理解决.
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
为促进国民身体健康,国家卫生健康委员会2025年在新闻发布会上提出将开展为期3年的"体重管理年"活动.某校为了解高一同学的体重情况,从高一年级随机抽取了66名学生,统计了他们的体重(单位:千克),并绘制了如下的茎叶图:
(1)为了解学生"体重低于75千克"是否与学生"性别"有关,将上述数据绘制成如下的列联表:
①将列联表补充完整;
②是否有的把握认为学生"体重低于75千克"与学生"性别"有关,说明理由;
(2)现从该校高一年级随机抽取200名学生,用(1)中的频率估计概率,则体重不少于75千克的学生最有可能有多少名?附:,
【答案】(1)①见解析 ②有关 (3)可能是27人
【解析】(1)①列联表如下:
②原假设:学生体重低于75千克与学生性别无关.
取显著性水平,∵拒绝原假设,
∴有的把握认为学生体重低于75千克与学生性别有关.
(2)体重不低于75千克的学生的频率为,记选出的学生中体重不低于75千克的人数为,则,即要求使得最大,,
∵,
∴,
令,则,
∴,
∴当时,最大,∴体重不低于75的最有可能是27人.
20.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知双曲线的右焦点分别为,直线与双曲线的左右支分别交于两点,且.
(1)当时,求双曲线的离心率;
(2)当时,求的面积;
(3)当时,求证:以和为邻边的矩形周长大于.
【答案】(1) (2) (3)证明见解析
【解析】(1)由题意,当时,令,则,
即,∴,
∴离心率.
(2)设左焦点为,
由对称性知,∴,即双曲线为,
令,则,
设线段与轴交于点,则,
∵,解得,
∴.
(3)令,则,
∵,∴
∵,即,即,
∵,令,
则,
当且仅当时,等号成立.因此,
∴周长为.
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数存在极值,并且其导函数的极值点是的零点,则称函数具有性质.
(1)判断函数和是否具有性质,并说明理由;
(2)设函数,求证:函数不具有性质;
(3)若函数具有性质,记函数和的所有极值之和为,求证:""是""的充分非必要条件.
【答案】(1)具有,不具有 (2)证明见解析 (3)证明见解析
【解析】(1)极值点为是的零点,所以具有性质P.
极值点为时,,所以不具有性质P.
(2),
①恒成立,无极值点,不具有性质P;
②极值点为,对,
若即时,恒成立,无极值点,不具有性质P;
若即时,,代入得;
所以,令,单调递减,不成立,不具有性质P;
充分性:,极值点为,由,得,
一定有两变号零点,设为,
极值点为,
所以,
非必要性:时,.
2025.5
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的值域为 .
2.设i是虚数单位,则 .
3.一组统计数据为,则该组数据的第85百分位数是 .
4.不等式的解集为 .
5.椭圆的焦距为 .
6.已知向量,则 .
7.若二项式的展开式中存在常数项,则正整数的最小值为 .
8.在中,边依次成等比数列,则内角的最大值为 .
9.从5个函数中随机选出两个函数,记选出的两个函数中,图像经过第二象限的函数的个数为,则的数学期望为 .
10.在平面直角坐标系中,已知点,点在抛物线上,若,则点横坐标的取值范围为 .
11.某生产线有一批边长相等的正方形铁皮,用每一块铁皮都可以加工出一个无盖的正四棱锥容器.具体的加工方式为:裁下图1中的阴影部分,余下的四个全等的等腰三角形作为容器的侧面(如图2).现要求每个容器的容积要达到最大,则在裁剪铁皮时应保证余下的等腰三角形的底角大小为 .
(第11题图1) (第11题图2)
12.设集合由所有满足下列条件的有序数组构成:①每一个元素等于中之一;②,则中元素个数为 .
二、选择题(本大题共有4题,满分18分,13-14每题4分,15-16每题5分).
13.已知集合满足,则( ).
A.P B.N C.M D.
14.在四面体中,分别是的重心,则与平面平行的棱有( ).
A.0条 B.1条 C.2条 D.3条
15.已知数列是正项等差数列,前项和为,则( ).
A.数列一定是等比数列 B.数列一定是等比数列
C.数列一定是等差数列 D.数列一定是等差数列
16.已知函数的定义域为[],对定义域内任意的的取值为或.有如下两个命题:
①若有且仅有2025个实数使得关于的方程只有1个解,则函数至少存在2025个严格减区间;
②若对任意满足条件的函数,方程都有解,则实数存在8101个可能的取值;则( ).
A.①正确; ②正确 B.①正确;②错误
C.①错误;②正确 D.①错误;②错误
三、解答题(本大题共5题,满分78分).
17.(本题满分14分,共有2个小题,第1小题满分6分,第2小题满分8分.)
已知函数的两个相邻极值点为和.
(1)求函数的解析式;
(2)设是锐角的内角,,求的取值范围.
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,直四棱柱的底面是边长为2的菱形,,侧面积为.点为和的交点,点是棱上一个动点,且不与顶点重合.
(1)当时,求的值;
(2)若锐二面角的余弦值为,求的值.
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
为促进国民身体健康,国家卫生健康委员会2025年在新闻发布会上提出将开展为期3年的"体重管理年"活动.某校为了解高一同学的体重情况,从高一年级随机抽取了66名学生,统计了他们的体重(单位:千克),并绘制了如下的茎叶图:
(1)为了解学生"体重低于75千克"是否与学生"性别"有关,将上述数据绘制成如下的列联表:
①将列联表补充完整;
②是否有的把握认为学生"体重低于75千克"与学生"性别"有关,说明理由;
(2)现从该校高一年级随机抽取200名学生,用(1)中的频率估计概率,则体重不少于75千克的学生最有可能有多少名?附:,
20.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知双曲线的右焦点分别为,直线与双曲线的左右支分别交于两点,且.
(1)当时,求双曲线的离心率;
(2)当时,求的面积;
(3)当时,求证:以和为邻边的矩形周长大于.
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数存在极值,并且其导函数的极值点是的零点,则称函数具有性质.
(1)判断函数和是否具有性质,并说明理由;
(2)设函数,求证:函数不具有性质;
(3)若函数具有性质,记函数和的所有极值之和为,求证:""是""的充分非必要条件.
华二2024-2025学年第二学期高三年级数学冲刺卷4
2025.5
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的值域为 .
【答案】
2.设i是虚数单位,则 .
【答案】1
3.一组统计数据为,则该组数据的第85百分位数是 .
【答案】99
4.不等式的解集为 .
【答案】
5.椭圆的焦距为 .
【答案】4
6.已知向量,则 .
【答案】
7.若二项式的展开式中存在常数项,则正整数的最小值为 .
【答案】11
8.在中,边依次成等比数列,则内角的最大值为 .
【答案】
9.从5个函数中随机选出两个函数,记选出的两个函数中,图像经过第二象限的函数的个数为,则的数学期望为 .
【答案】
10.在平面直角坐标系中,已知点,点在抛物线上,若,则点横坐标的取值范围为 .
【答案】
11.某生产线有一批边长相等的正方形铁皮,用每一块铁皮都可以加工出一个无盖的正四棱锥容器.具体的加工方式为:裁下图1中的阴影部分,余下的四个全等的等腰三角形作为容器的侧面(如图2).现要求每个容器的容积要达到最大,则在裁剪铁皮时应保证余下的等腰三角形的底角大小为 .
(第11题图1) (第11题图2)
【答案】
12.设集合由所有满足下列条件的有序数组构成:①每一个元素等于中之一;②,则中元素个数为 .
【答案】169
二、选择题(本大题共有4题,满分18分,13-14每题4分,15-16每题5分).
13.已知集合满足,则( ).
A.P B.N C.M D.
【答案】A
14.在四面体中,分别是的重心,则与平面平行的棱有( ).
A.0条 B.1条 C.2条 D.3条
【答案】B
15.已知数列是正项等差数列,前项和为,则( ).
A.数列一定是等比数列 B.数列一定是等比数列
C.数列一定是等差数列 D.数列一定是等差数列
【答案】
16.已知函数的定义域为[],对定义域内任意的的取值为或.有如下两个命题:
①若有且仅有2025个实数使得关于的方程只有1个解,则函数至少存在2025个严格减区间;
②若对任意满足条件的函数,方程都有解,则实数存在8101个可能的取值;则( ).
A.①正确; ②正确 B.①正确;②错误
C.①错误;②正确 D.①错误;②错误
【答案】
三、解答题(本大题共5题,满分78分).
17.(本题满分14分,共有2个小题,第1小题满分6分,第2小题满分8分.)
已知函数的两个相邻极值点为和.
(1)求函数的解析式;
(2)设是锐角的内角,,求的取值范围.
【答案】(1) (2)
【解析】(1)由题意,即,
即
(2)
且
即
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图,直四棱柱的底面是边长为2的菱形,,侧面积为.点为和的交点,点是棱上一个动点,且不与顶点重合.
(1)当时,求的值;
(2)若锐二面角的余弦值为,求的值.
【答案】(1) (2)或
【解析】(1)棱柱高,在菱形中,
以为原点,所在直线为轴建立空间直角坐标系(如图).则,设长为,则,
∴,即.
(2),
设平面的法向量为,则,
即,令,则
∵,设平面的法向量为,
则即令,则
设锐二面角的平面角为,则,
解得或或.
【解法2】(1)运用三垂线定理;(2)借助二面角平面角的定理,利用余弦定理解决.
19.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
为促进国民身体健康,国家卫生健康委员会2025年在新闻发布会上提出将开展为期3年的"体重管理年"活动.某校为了解高一同学的体重情况,从高一年级随机抽取了66名学生,统计了他们的体重(单位:千克),并绘制了如下的茎叶图:
(1)为了解学生"体重低于75千克"是否与学生"性别"有关,将上述数据绘制成如下的列联表:
①将列联表补充完整;
②是否有的把握认为学生"体重低于75千克"与学生"性别"有关,说明理由;
(2)现从该校高一年级随机抽取200名学生,用(1)中的频率估计概率,则体重不少于75千克的学生最有可能有多少名?附:,
【答案】(1)①见解析 ②有关 (3)可能是27人
【解析】(1)①列联表如下:
②原假设:学生体重低于75千克与学生性别无关.
取显著性水平,∵拒绝原假设,
∴有的把握认为学生体重低于75千克与学生性别有关.
(2)体重不低于75千克的学生的频率为,记选出的学生中体重不低于75千克的人数为,则,即要求使得最大,,
∵,
∴,
令,则,
∴,
∴当时,最大,∴体重不低于75的最有可能是27人.
20.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知双曲线的右焦点分别为,直线与双曲线的左右支分别交于两点,且.
(1)当时,求双曲线的离心率;
(2)当时,求的面积;
(3)当时,求证:以和为邻边的矩形周长大于.
【答案】(1) (2) (3)证明见解析
【解析】(1)由题意,当时,令,则,
即,∴,
∴离心率.
(2)设左焦点为,
由对称性知,∴,即双曲线为,
令,则,
设线段与轴交于点,则,
∵,解得,
∴.
(3)令,则,
∵,∴
∵,即,即,
∵,令,
则,
当且仅当时,等号成立.因此,
∴周长为.
21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若函数存在极值,并且其导函数的极值点是的零点,则称函数具有性质.
(1)判断函数和是否具有性质,并说明理由;
(2)设函数,求证:函数不具有性质;
(3)若函数具有性质,记函数和的所有极值之和为,求证:""是""的充分非必要条件.
【答案】(1)具有,不具有 (2)证明见解析 (3)证明见解析
【解析】(1)极值点为是的零点,所以具有性质P.
极值点为时,,所以不具有性质P.
(2),
①恒成立,无极值点,不具有性质P;
②极值点为,对,
若即时,恒成立,无极值点,不具有性质P;
若即时,,代入得;
所以,令,单调递减,不成立,不具有性质P;
充分性:,极值点为,由,得,
一定有两变号零点,设为,
极值点为,
所以,
非必要性:时,.
同课章节目录
