6.2 第1课时 用代入法解二元一次方程组 课件(共26张PPT)
文档属性
| 名称 | 6.2 第1课时 用代入法解二元一次方程组 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
华东师大版数学七年级下册
第6章 一次方程组
汇报人:孙老师
汇报班级:X级X班
6.2 第1课时 用代入法解二元一次方程组
6.2 二元一次方程组的解法
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解解二元一次方程组的基本思想一消元思想.
2.会用代入法解二元一次方程组.
第贰章节
新课导入
新课导入
我们先来回顾6.1节中的问题2.
在问题2中,如果设应拆除x m2旧校舍,建造y m2新
校舍,那么根据题意可列出方程组
怎样求这个二元一次方程组的解呢
①
②
第叁章节
新知探究
新知探究
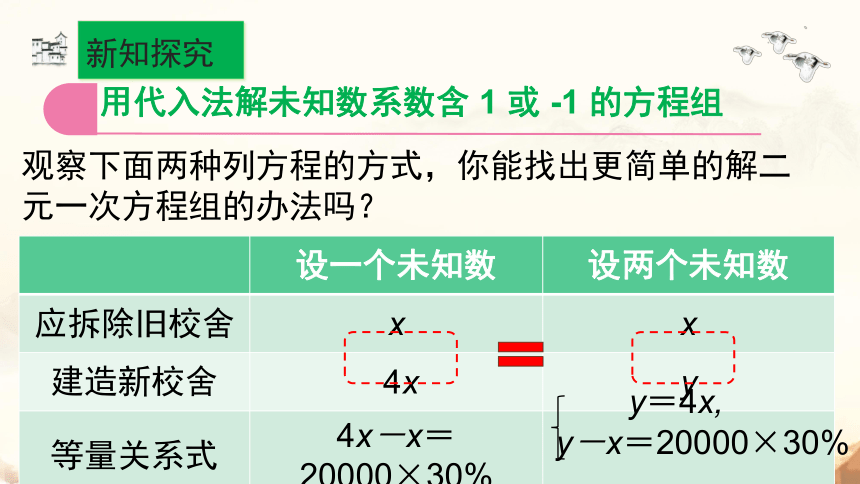
观察下面两种列方程的方式,你能找出更简单的解二元一次方程组的办法吗?
设一个未知数 设两个未知数
应拆除旧校舍 x x
建造新校舍 4x y
等量关系式 4x-x=20000×30%
y-x=20000×30%
y=4x,
用代入法解未知数系数含 1 或 -1 的方程组
∠1 = ∠2
y -x=20000×30%
4x
4x-x=20000×30%
①
②
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
总结
y = 4x
合作探究
y-x=20000×30%,
y=4x.
答:应拆除 2000 m2 旧校舍,建造 8000 m2 新校舍.
解 :把②代入①,得 4x-x=20000×30%,
3x=6000,
x=2000.
把 x=2000 代入②,得
y=8000.
所以
x=2000,
y=8000.
解方程组
①
②
解二元一次方程组的基本思路:“消元”
二元一次方程组
一元一次方程
消元
转化
通过代入消去一个未知数,将方程组转化为一元一次方程来解的,这种解法叫做代入消元法,简称代入法.
归纳总结
将 x = 5 代入③ ,得 y = 2.
所以原方程组的解是
x = 5 ,
y = 2.
解:由 ①,得 y = 7 - x, ③
将 ③ 代入 ②,得 3x + 7 - x = 17.
2x = 10
x = 5.
例1 解方程组:
x + y = 7, ①
3x + y = 17. ②
转化
代入
求解
回代
写解
注意:检验方程组的解.
典例精析
代入消元法解二元一次方程组的一般步骤:
转化
代入
求解
回代
写解
检验
由①得
y=7-x③
将③代入②
3x+7-x =17
解得x=5
x+y = 7,①
3x+y = 17 ②
将x=5代入①,得y=2
举例:
方法总结
将 y = -3 代入 ③ ,得 x = -3.
所以原方程组的解是
x = -3,
y = -3.
解:由 ②,得 x = -15 - 4y, ③
将 ③ 代入 ①,得 3(-15 - 4y) - 5y = 6,
-45 - 12y - 5y = 6,
-17y = 51,
y = -3.
例2 解方程组:
3x-5y = 6, ①
x + 4y = -15. ②
典例精析
x + 3y = 8,①
5x + 3y = 16. ②
1. 解二元一次方程组:
解:由 ① 得 x = 8-3y. ③
将 ③ 代入 ② 得
5(8-3y) + 3y = 16.
解得 y = 2.
把 y = 2 代入 ③,得 x = 2.
所以原方程组的解为
x = 2,
y = 2.
解:由 ① 得 3y = 8-x. ③
将 ③ 代入 ② 得
5x + 8-x = 16.
解得 x = 2.
把 x = 2 代入 ③,得 y = 2.
所以原方程组的解为
x = 2,
y = 2.
练一练
2. 篮球联赛中,每场比赛都要分出胜负,胜一场得 2 分,负一场得 1 分.某队为了争取较好的名次,想在全部 20 场比赛中得到 35 分,那么这个队胜负场数分别是多少?
等量关系:
(1) 胜球场数 + 负球场数 = 全部场数;
(2) 胜球得分 + 负球得分 = 总得分.
练一练
解: 设胜的场数是 x,负的场数是 y,
可列方程组:
由①得 y=20 - x . ③
将③代入②,得 2x + 20 - x = 35 ,
解得 x = 15.
将 x = 15 代入③得 y = 5.
则这个方程组的解是
答:这个队胜 15 场,负 5 场.
①
②
第肆章节
随堂练习
随堂练习
1. 把下列各方程变形为用一个未知数的代数式表示
另一个未知数的形式:
(1)4x-y = -1;
(2)5x-10y + 15 = 0 .
解:(1)y = 4x + 1或
(2)x = 2y - 3或
2. 解下列方程组:
2x -4y = 6,
3x + 2y = 17.
(1)
①
②
解 由 ① ,得
x = 2y + 3 . ③
将③代入 ② ,得
3(2y + 3) + 2y = 17.
解得 y = 1.
将 y = 1 代入③,得 x = 5.
x = 5 ,
y = 1 .
所以
3y = x + 4,
2x + 5y = -19.
(2)
①
②
解 由 ① ,得
x = 3y -4. ③
将③代入② ,得
2(3y-4) + 5y = -19.
解得 y = -1.
将 y = -1 代入③,得 x = -7.
x = -7,
y = -1 .
所以
2x + 3y = 7,
3x - 5y = 1.
(3)
①
②
解 由①,得
x = ③
7-3y
2
将③代入②,得
3× -5y = 1.
7-3y
2
解得 y = 1.
将 y = 1 代入③,得 x = 2 .
x = 2,
y = 1 .
所以
3x + 5y = 5,
3x - 4y = 23.
(4)
①
②
解 由①,得
x = ③
5-5y
3
将③代入②,得
3× -4y = 23.
5-5y
3
解得 y = -2.
将 y = -2 代入③,得 x = 5 .
x = 5,
y = -2 .
所以
第伍章节
课堂小结
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第6章 一次方程组
汇报人:孙老师
汇报班级:X级X班
6.2 第1课时 用代入法解二元一次方程组
6.2 二元一次方程组的解法
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解解二元一次方程组的基本思想一消元思想.
2.会用代入法解二元一次方程组.
第贰章节
新课导入
新课导入
我们先来回顾6.1节中的问题2.
在问题2中,如果设应拆除x m2旧校舍,建造y m2新
校舍,那么根据题意可列出方程组
怎样求这个二元一次方程组的解呢
①
②
第叁章节
新知探究
新知探究
观察下面两种列方程的方式,你能找出更简单的解二元一次方程组的办法吗?
设一个未知数 设两个未知数
应拆除旧校舍 x x
建造新校舍 4x y
等量关系式 4x-x=20000×30%
y-x=20000×30%
y=4x,
用代入法解未知数系数含 1 或 -1 的方程组
∠1 = ∠2
y -x=20000×30%
4x
4x-x=20000×30%
①
②
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
总结
y = 4x
合作探究
y-x=20000×30%,
y=4x.
答:应拆除 2000 m2 旧校舍,建造 8000 m2 新校舍.
解 :把②代入①,得 4x-x=20000×30%,
3x=6000,
x=2000.
把 x=2000 代入②,得
y=8000.
所以
x=2000,
y=8000.
解方程组
①
②
解二元一次方程组的基本思路:“消元”
二元一次方程组
一元一次方程
消元
转化
通过代入消去一个未知数,将方程组转化为一元一次方程来解的,这种解法叫做代入消元法,简称代入法.
归纳总结
将 x = 5 代入③ ,得 y = 2.
所以原方程组的解是
x = 5 ,
y = 2.
解:由 ①,得 y = 7 - x, ③
将 ③ 代入 ②,得 3x + 7 - x = 17.
2x = 10
x = 5.
例1 解方程组:
x + y = 7, ①
3x + y = 17. ②
转化
代入
求解
回代
写解
注意:检验方程组的解.
典例精析
代入消元法解二元一次方程组的一般步骤:
转化
代入
求解
回代
写解
检验
由①得
y=7-x③
将③代入②
3x+7-x =17
解得x=5
x+y = 7,①
3x+y = 17 ②
将x=5代入①,得y=2
举例:
方法总结
将 y = -3 代入 ③ ,得 x = -3.
所以原方程组的解是
x = -3,
y = -3.
解:由 ②,得 x = -15 - 4y, ③
将 ③ 代入 ①,得 3(-15 - 4y) - 5y = 6,
-45 - 12y - 5y = 6,
-17y = 51,
y = -3.
例2 解方程组:
3x-5y = 6, ①
x + 4y = -15. ②
典例精析
x + 3y = 8,①
5x + 3y = 16. ②
1. 解二元一次方程组:
解:由 ① 得 x = 8-3y. ③
将 ③ 代入 ② 得
5(8-3y) + 3y = 16.
解得 y = 2.
把 y = 2 代入 ③,得 x = 2.
所以原方程组的解为
x = 2,
y = 2.
解:由 ① 得 3y = 8-x. ③
将 ③ 代入 ② 得
5x + 8-x = 16.
解得 x = 2.
把 x = 2 代入 ③,得 y = 2.
所以原方程组的解为
x = 2,
y = 2.
练一练
2. 篮球联赛中,每场比赛都要分出胜负,胜一场得 2 分,负一场得 1 分.某队为了争取较好的名次,想在全部 20 场比赛中得到 35 分,那么这个队胜负场数分别是多少?
等量关系:
(1) 胜球场数 + 负球场数 = 全部场数;
(2) 胜球得分 + 负球得分 = 总得分.
练一练
解: 设胜的场数是 x,负的场数是 y,
可列方程组:
由①得 y=20 - x . ③
将③代入②,得 2x + 20 - x = 35 ,
解得 x = 15.
将 x = 15 代入③得 y = 5.
则这个方程组的解是
答:这个队胜 15 场,负 5 场.
①
②
第肆章节
随堂练习
随堂练习
1. 把下列各方程变形为用一个未知数的代数式表示
另一个未知数的形式:
(1)4x-y = -1;
(2)5x-10y + 15 = 0 .
解:(1)y = 4x + 1或
(2)x = 2y - 3或
2. 解下列方程组:
2x -4y = 6,
3x + 2y = 17.
(1)
①
②
解 由 ① ,得
x = 2y + 3 . ③
将③代入 ② ,得
3(2y + 3) + 2y = 17.
解得 y = 1.
将 y = 1 代入③,得 x = 5.
x = 5 ,
y = 1 .
所以
3y = x + 4,
2x + 5y = -19.
(2)
①
②
解 由 ① ,得
x = 3y -4. ③
将③代入② ,得
2(3y-4) + 5y = -19.
解得 y = -1.
将 y = -1 代入③,得 x = -7.
x = -7,
y = -1 .
所以
2x + 3y = 7,
3x - 5y = 1.
(3)
①
②
解 由①,得
x = ③
7-3y
2
将③代入②,得
3× -5y = 1.
7-3y
2
解得 y = 1.
将 y = 1 代入③,得 x = 2 .
x = 2,
y = 1 .
所以
3x + 5y = 5,
3x - 4y = 23.
(4)
①
②
解 由①,得
x = ③
5-5y
3
将③代入②,得
3× -4y = 23.
5-5y
3
解得 y = -2.
将 y = -2 代入③,得 x = 5 .
x = 5,
y = -2 .
所以
第伍章节
课堂小结
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
