8.2 第2课时 多边形的外角和 课件(共25张PPT)
文档属性
| 名称 | 8.2 第2课时 多边形的外角和 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
华东师大版数学七年级下册
第8章 三角形
汇报人:孙老师
汇报班级:X级X班
第2课时 多边形的外角和
8.2 多边形的内角和与外角和
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解多边形外角和的推导,并掌握多边形的外角和.
2.运用多边形的外角和解决问题.
第贰章节
新课导入
新课导入
1. 从 n 边形的一个顶点出发可以引________条对角线,它们把 n 边形分成________个三角形.
(n – 3)
(n – 2)
3. 多边形的内角和公式:_________________.
(n – 2)·180°
4. 正 n 边形的每一个内角的度数为____________.
2. 一个 n 边形有__________条对角线.
第叁章节
新知探究
新知探究
多边形的外角和
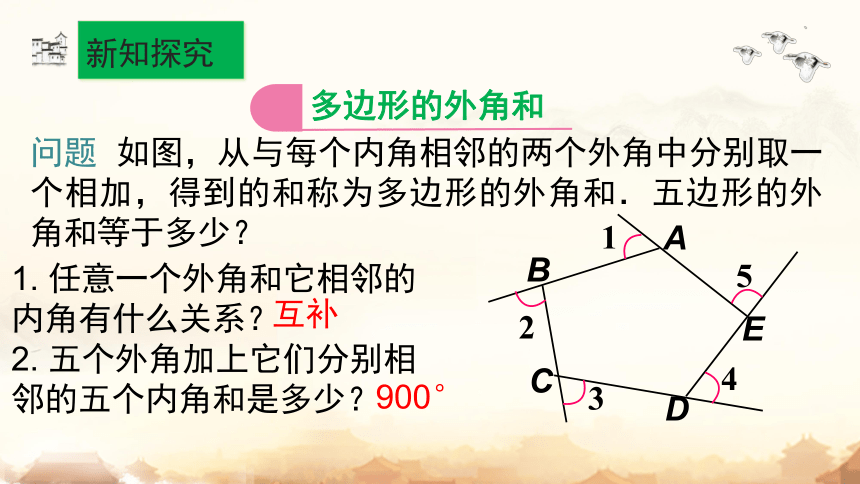
问题 如图,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.五边形的外角和等于多少?
1. 任意一个外角和它相邻的内角有什么关系?
2. 五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
900°
E
B
C
D
1
2
3
4
5
A
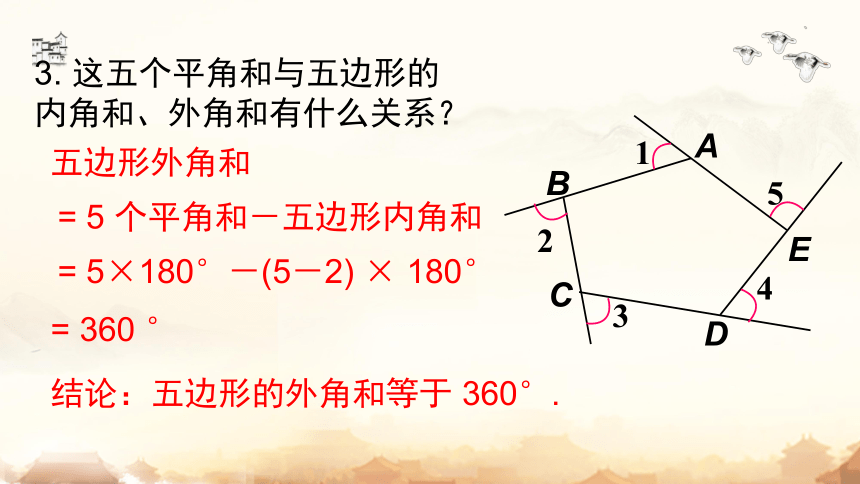
五边形外角和
= 360 °
= 5 个平角和-五边形内角和
= 5×180°-(5-2) × 180°
结论:五边形的外角和等于 360°.
3. 这五个平角和与五边形的内角和、外角和有什么关系?
与 n 边形的每个内角相邻的外角分别有两个, 这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为 n 边形的外角和.
n 边形外角和
=360 °
= n 个平角和-n 边形内角和
= n×180 °-(n-2) × 180°
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和等于 360°.
归纳总结
多边形外角和公式:
例1 已知一个多边形,它的内角和等于外角和的 5 倍,求这个多边形的边数.
解: 设多边形的边数为 n.
∵它的内角和等于 (n-2)·180°,
多边形外角和等于 360°,
∴ (n-2)·180°= 5× 360 .
解得 n = 12. ∴这个多边形的边数为 12.
变式:一个多边形的外角和是内角和的 ,则其边数 n为 .
12
典例精析
例 2 已知一个多边形的每个内角与外角的比都
是 7∶2,求这个多边形的边数.
解法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即每个内角是 140°,每个外角是 40°.
360°÷40° = 9.
答:这个多边形的边数为 9.
还有其他解法吗?
解法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形的边数为 9.
第肆章节
随堂练习
随堂练习
1. 一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
解:360°÷45°= 8,
【教材P99练习 第1题】
180°– 45°= 135°.
因此,这个多边形是八边形,它的每一个内角是 135°.
2. 在一个多边形中,它的内角最多可以有几个是锐角?
解:根据多边形的外角和可知,
多边形的外角最多可以有 3 个钝角,
所以多边形的内角最多可以有 3 个锐角.
【教材P99练习 第2题】
3. 一个多边形的内角和等于它的外角和的 3 倍,它是几边形?
解:设这个多边形是 n 边形,则它的内角和是(n – 2)·180°,外角和等于 360°,
所以 (n – 2)·180°= 3×360°.
解得 n = 8
因此,这个多边形是八边形.
4. 如图,状状从点 A 出发沿直线前进10 米,后左转 30 度,再沿直线前进 10 米. 又向左转 30 度,…,照这样走下去,他第一次回到出发地 A 点时,一共走了多少米?
解:由题意可知,小亮第一次回到出发地 A 点时,他的行走路线是一个正多边形,且这个正多边形的外角等于 30°,边长为10 米. 所以这个多边形的边数为
所以一共走了12×10 = 120(米).
5. 如图,用 n 个完全相同的正五边形进行拼接,使相邻的两个正五边形有一条公共边,围成一圈后中间形成一个正 n 边形,则 n 的值等于______.
10
6. 将正三角形、正方形、正五边形按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则∠1 +∠2 +∠3 =______.
102°
1
3
2
第伍章节
课堂小结
课堂小结
多边形的外角和定理
多边形的外角和等于360°
特别注意:与边数无关。
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第8章 三角形
汇报人:孙老师
汇报班级:X级X班
第2课时 多边形的外角和
8.2 多边形的内角和与外角和
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解多边形外角和的推导,并掌握多边形的外角和.
2.运用多边形的外角和解决问题.
第贰章节
新课导入
新课导入
1. 从 n 边形的一个顶点出发可以引________条对角线,它们把 n 边形分成________个三角形.
(n – 3)
(n – 2)
3. 多边形的内角和公式:_________________.
(n – 2)·180°
4. 正 n 边形的每一个内角的度数为____________.
2. 一个 n 边形有__________条对角线.
第叁章节
新知探究
新知探究
多边形的外角和
问题 如图,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.五边形的外角和等于多少?
1. 任意一个外角和它相邻的内角有什么关系?
2. 五个外角加上它们分别相邻的五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
900°
E
B
C
D
1
2
3
4
5
A
五边形外角和
= 360 °
= 5 个平角和-五边形内角和
= 5×180°-(5-2) × 180°
结论:五边形的外角和等于 360°.
3. 这五个平角和与五边形的内角和、外角和有什么关系?
与 n 边形的每个内角相邻的外角分别有两个, 这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为 n 边形的外角和.
n 边形外角和
=360 °
= n 个平角和-n 边形内角和
= n×180 °-(n-2) × 180°
E
B
C
D
1
2
3
4
n
A
任意多边形的外角和等于 360°.
归纳总结
多边形外角和公式:
例1 已知一个多边形,它的内角和等于外角和的 5 倍,求这个多边形的边数.
解: 设多边形的边数为 n.
∵它的内角和等于 (n-2)·180°,
多边形外角和等于 360°,
∴ (n-2)·180°= 5× 360 .
解得 n = 12. ∴这个多边形的边数为 12.
变式:一个多边形的外角和是内角和的 ,则其边数 n为 .
12
典例精析
例 2 已知一个多边形的每个内角与外角的比都
是 7∶2,求这个多边形的边数.
解法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即每个内角是 140°,每个外角是 40°.
360°÷40° = 9.
答:这个多边形的边数为 9.
还有其他解法吗?
解法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形的边数为 9.
第肆章节
随堂练习
随堂练习
1. 一个多边形的每一个外角都等于 45°,这个多边形是几边形?它的每一个内角是多少度?
解:360°÷45°= 8,
【教材P99练习 第1题】
180°– 45°= 135°.
因此,这个多边形是八边形,它的每一个内角是 135°.
2. 在一个多边形中,它的内角最多可以有几个是锐角?
解:根据多边形的外角和可知,
多边形的外角最多可以有 3 个钝角,
所以多边形的内角最多可以有 3 个锐角.
【教材P99练习 第2题】
3. 一个多边形的内角和等于它的外角和的 3 倍,它是几边形?
解:设这个多边形是 n 边形,则它的内角和是(n – 2)·180°,外角和等于 360°,
所以 (n – 2)·180°= 3×360°.
解得 n = 8
因此,这个多边形是八边形.
4. 如图,状状从点 A 出发沿直线前进10 米,后左转 30 度,再沿直线前进 10 米. 又向左转 30 度,…,照这样走下去,他第一次回到出发地 A 点时,一共走了多少米?
解:由题意可知,小亮第一次回到出发地 A 点时,他的行走路线是一个正多边形,且这个正多边形的外角等于 30°,边长为10 米. 所以这个多边形的边数为
所以一共走了12×10 = 120(米).
5. 如图,用 n 个完全相同的正五边形进行拼接,使相邻的两个正五边形有一条公共边,围成一圈后中间形成一个正 n 边形,则 n 的值等于______.
10
6. 将正三角形、正方形、正五边形按如图所示的位置摆放,且每一个图形的一个顶点都在另一个图形的一条边上,则∠1 +∠2 +∠3 =______.
102°
1
3
2
第伍章节
课堂小结
课堂小结
多边形的外角和定理
多边形的外角和等于360°
特别注意:与边数无关。
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
