9.1.2 轴对称的再认识 课件(共31张PPT)
文档属性
| 名称 | 9.1.2 轴对称的再认识 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 09:15:39 | ||
图片预览








文档简介
(共31张PPT)
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.1.2 轴对称的再认识
9.1 轴对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索线段、角等简单图形的轴对称性,能用尺规作已知线段的垂直平分线、角的平分线.
2.掌握其他复杂的轴对称图形的对称轴的作法.
第贰章节
新课导入
新课导入
如图,△ABC是轴对称图形,AD所在的直线是它的对称轴,根据轴对称图形的基本特征,你能得出什么结论?
对应线段相等:
AB=AC,BD=CD
对应角相等:
∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC
观察线段和角,它们都是轴对称图形吗?
第叁章节
新知探究
新知探究
1
线段的垂直平分线
探究一:观察线段,它是轴对称图形吗
如图,在半透明纸上画出线段 AB,对折线段 AB,使点 A 与点 B 重合,在折痕上任取两点 P、Q,然后用直尺画出折痕 PQ,直线 PQ 与线段 AB 相交于点O.
对折后,线段 OA 与 OB 是否重合 ∠POA 与∠POB 是否重合
你能说明直线 PQ 与线段 AB 的关系吗
(A)
B
P
Q
O
A
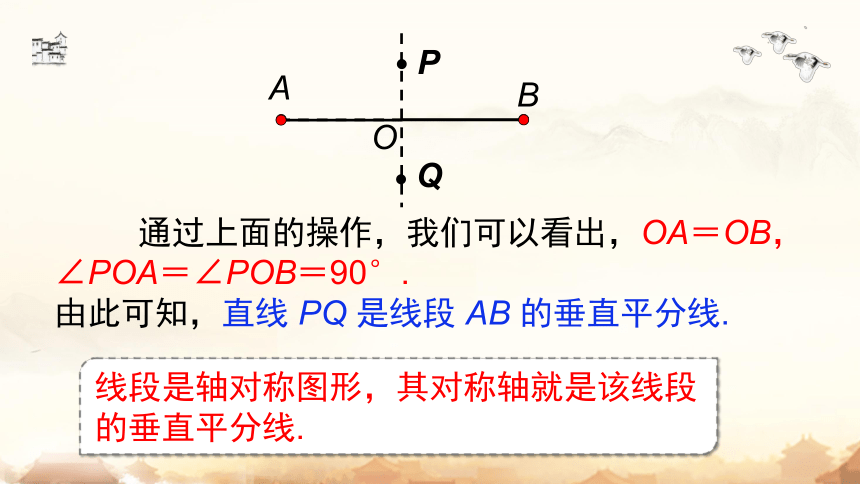
通过上面的操作,我们可以看出,OA=OB,
∠POA=∠POB=90°.
由此可知,直线 PQ 是线段 AB 的垂直平分线.
线段是轴对称图形,其对称轴就是该线段的垂直平分线.
A
B
O
Q
P
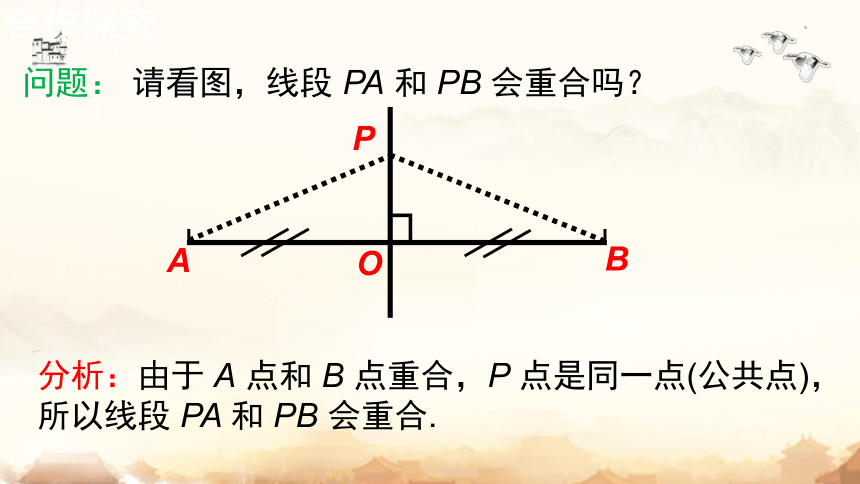
问题: 请看图,线段 PA 和 PB 会重合吗?
A
B
O
P
分析:由于 A 点和 B 点重合,P 点是同一点(公共点),所以线段 PA 和 PB 会重合.
合作探究
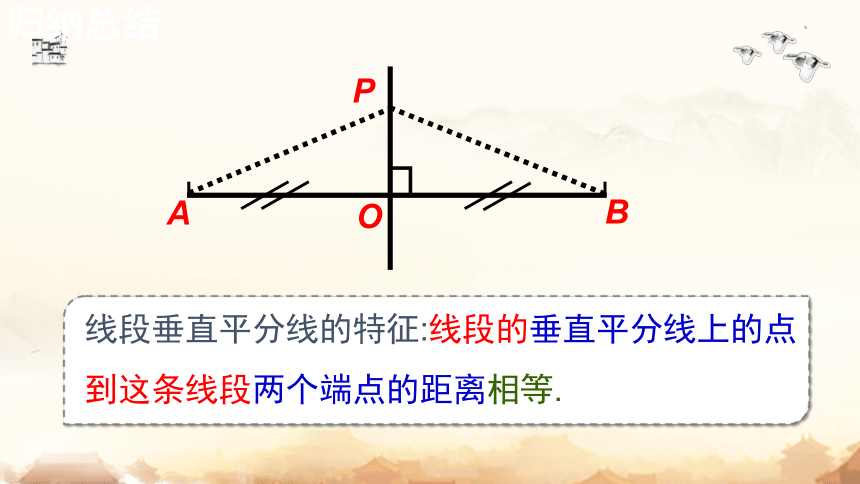
线段垂直平分线的特征:线段的垂直平分线上的点到这条线段两个端点的距离相等.
归纳总结
A
B
O
P
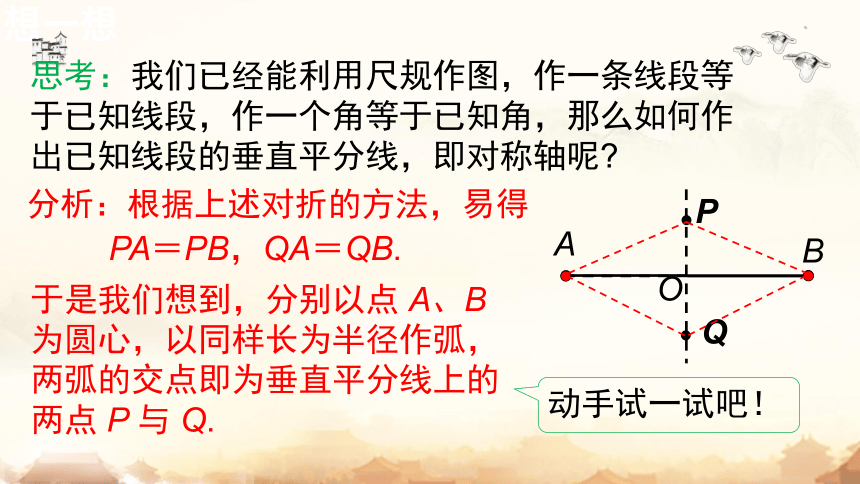
思考:我们已经能利用尺规作图,作一条线段等于已知线段,作一个角等于已知角,那么如何作出已知线段的垂直平分线,即对称轴呢
A
B
O
Q
P
分析:根据上述对折的方法,易得
PA=PB,QA=QB.
于是我们想到,分别以点 A、B 为圆心,以同样长为半径作弧,两弧的交点即为垂直平分线上的两点 P 与 Q.
动手试一试吧!
想一想
利用尺规,作线段 AB 的垂直平分线.
作法:(1) 分别以点A和B为圆心、相同长(大于线段 AB 长的一半)为半径作弧,两弧分别相交于点 P 和点 Q;
已知:线段 AB.
求作:AB 的垂直平分线.
(2) 作直线 PQ.
直线 PQ 就是所要求作的线段 AB 的垂直平分线.
A
B
P
Q
画一画
例 △ABC 中,BC=10,边 BC 的
垂直平分线分别交 AB、BC 于点
E、D,BE=6,求△BCE 的周长.
解:∵ ED 是 BC 的垂直平分线,(已知)
∴EC = EB = 6.
(线段的垂直平分线上的点到这条线段两个端点
的距离相等)
∴△BCE 的周长=BC+CE+EB=10+6+6=22.
答:△BCE的周长为 22.
典例精析
探究二:现在我们已经知道,线段是轴对称图形,那么常见的角是否也是轴对称图形呢
2
角的对称轴
如图,在半透明纸上画出∠AOB,对折∠AOB,使角的两边完全重合,然后在折痕(角的内部)
上任取一点 P,用直尺画出折痕 OP,显然射线 OP 是该角的平分线,看看直线OP与∠AOB 是什么关系.
O
A
B
P
O
A
B
P
通过上面的操作,我们可以看出,
∠AOP=∠BOP.
角也是轴对称图形,其对称轴是这个角的平分线所在的直线.
强调:角平分线是一条射线,而角的对称轴是角平分线所在的直线.
思考:我们已经能利用尺规作图作出已知线段的垂直平分线,那么如何作出已知角的平分线,从而得到已知角的对称轴呢
提问:根据上述对折的方法,将 ∠AOB 对折两半重合,在边 OA 上任取一点 M,它与边 OB 上一点 N 重合,此时能够得到什么?
OM = ON,PM = PN
于是我们想到,以点 O 为圆心作弧,交∠AOB 两边于 M、N. 再分别以 M、N 为圆心,等长(大于线段MN长的一半)为半径作弧,两弧交于点 P,点P 即为角平分线上一点.
O
A
B
P
M
N
动手试一试吧!
想一想
作法:(1) 以点 O 为圆心,任意长为半径作弧,与角的两边分别交于 M、N 两点;
A
B
M
N
P
O
已知:∠AOB.
求作:∠AOB 的平分线.
仔细观察作图步骤
画一画
(3) 作射线 OP.
射线 OP 就是所要求作的∠AOB 的平分线.
(2) 分别以点 M 和 N 为圆心、相同长(大于线段 MN 长的一半)为半径作弧,在∠AOB 内,两弧相交于点 P;
轴对称图形对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格,且不能折叠,你还能比较准确的画出图形的对称轴吗?
3
1. 画出下面图形的对称轴,画完图后请思考下面的问题:
① 能总结你画对称轴的方法吗?
② 连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分.
合作探究
2. 如图,点 A 和点 A′ 关于某条直线成轴对称,你能画出这条直线吗?
A A′
(1) 找出图形的任意一组对称点;
画图形的对称轴的画法:
(2) 连结对称点;
(3) 画出对称点所连线段的垂直平分线.
就可以得到该图形的对称轴.
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
归纳总结
第肆章节
随堂练习
随堂练习
1.平面上的两条相交直线是轴对称图吗?如果是,它有几条对称轴?作图试试看.
解:是轴对称图形,对称轴有两条,是两直线夹角的平分线所在的直线(画图略).
【教材P120 练习 第1题】
2.把一张正方形纸对折两次,然后分别剪出下列图形.
解:(1)操作步骤如图①所示.
(2)操作步骤如图②所示.
【教材P120 练习 第2题】
3.图中的一些虚线,哪些是图形的对称轴,哪些不是?
②④⑥是图形的对称轴,①③⑤不是.
【教材P120 练习 第3题】
4.如图,已知△ABC ,利用尺规作图作出△ABC的边BC上的中线.
A
B
C
解:①作出线段BC的垂直平分线,交线段BC于点O;
②连接AO,线段AO即为△ABC的边BC 上的中线.
O
【教材P121 练习 第4题】
5.如图,已知△ABC ,利用尺规作图作出∠ABC的平分线.
A
B
C
O
【教材P121 练习 第5题】
第伍章节
课堂小结
课堂小结
线段和角
线段和角都是轴对称图形
尺规作图
轴对称的再认识
作轴对称图形的对称轴
如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.1.2 轴对称的再认识
9.1 轴对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索线段、角等简单图形的轴对称性,能用尺规作已知线段的垂直平分线、角的平分线.
2.掌握其他复杂的轴对称图形的对称轴的作法.
第贰章节
新课导入
新课导入
如图,△ABC是轴对称图形,AD所在的直线是它的对称轴,根据轴对称图形的基本特征,你能得出什么结论?
对应线段相等:
AB=AC,BD=CD
对应角相等:
∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC
观察线段和角,它们都是轴对称图形吗?
第叁章节
新知探究
新知探究
1
线段的垂直平分线
探究一:观察线段,它是轴对称图形吗
如图,在半透明纸上画出线段 AB,对折线段 AB,使点 A 与点 B 重合,在折痕上任取两点 P、Q,然后用直尺画出折痕 PQ,直线 PQ 与线段 AB 相交于点O.
对折后,线段 OA 与 OB 是否重合 ∠POA 与∠POB 是否重合
你能说明直线 PQ 与线段 AB 的关系吗
(A)
B
P
Q
O
A
通过上面的操作,我们可以看出,OA=OB,
∠POA=∠POB=90°.
由此可知,直线 PQ 是线段 AB 的垂直平分线.
线段是轴对称图形,其对称轴就是该线段的垂直平分线.
A
B
O
Q
P
问题: 请看图,线段 PA 和 PB 会重合吗?
A
B
O
P
分析:由于 A 点和 B 点重合,P 点是同一点(公共点),所以线段 PA 和 PB 会重合.
合作探究
线段垂直平分线的特征:线段的垂直平分线上的点到这条线段两个端点的距离相等.
归纳总结
A
B
O
P
思考:我们已经能利用尺规作图,作一条线段等于已知线段,作一个角等于已知角,那么如何作出已知线段的垂直平分线,即对称轴呢
A
B
O
Q
P
分析:根据上述对折的方法,易得
PA=PB,QA=QB.
于是我们想到,分别以点 A、B 为圆心,以同样长为半径作弧,两弧的交点即为垂直平分线上的两点 P 与 Q.
动手试一试吧!
想一想
利用尺规,作线段 AB 的垂直平分线.
作法:(1) 分别以点A和B为圆心、相同长(大于线段 AB 长的一半)为半径作弧,两弧分别相交于点 P 和点 Q;
已知:线段 AB.
求作:AB 的垂直平分线.
(2) 作直线 PQ.
直线 PQ 就是所要求作的线段 AB 的垂直平分线.
A
B
P
Q
画一画
例 △ABC 中,BC=10,边 BC 的
垂直平分线分别交 AB、BC 于点
E、D,BE=6,求△BCE 的周长.
解:∵ ED 是 BC 的垂直平分线,(已知)
∴EC = EB = 6.
(线段的垂直平分线上的点到这条线段两个端点
的距离相等)
∴△BCE 的周长=BC+CE+EB=10+6+6=22.
答:△BCE的周长为 22.
典例精析
探究二:现在我们已经知道,线段是轴对称图形,那么常见的角是否也是轴对称图形呢
2
角的对称轴
如图,在半透明纸上画出∠AOB,对折∠AOB,使角的两边完全重合,然后在折痕(角的内部)
上任取一点 P,用直尺画出折痕 OP,显然射线 OP 是该角的平分线,看看直线OP与∠AOB 是什么关系.
O
A
B
P
O
A
B
P
通过上面的操作,我们可以看出,
∠AOP=∠BOP.
角也是轴对称图形,其对称轴是这个角的平分线所在的直线.
强调:角平分线是一条射线,而角的对称轴是角平分线所在的直线.
思考:我们已经能利用尺规作图作出已知线段的垂直平分线,那么如何作出已知角的平分线,从而得到已知角的对称轴呢
提问:根据上述对折的方法,将 ∠AOB 对折两半重合,在边 OA 上任取一点 M,它与边 OB 上一点 N 重合,此时能够得到什么?
OM = ON,PM = PN
于是我们想到,以点 O 为圆心作弧,交∠AOB 两边于 M、N. 再分别以 M、N 为圆心,等长(大于线段MN长的一半)为半径作弧,两弧交于点 P,点P 即为角平分线上一点.
O
A
B
P
M
N
动手试一试吧!
想一想
作法:(1) 以点 O 为圆心,任意长为半径作弧,与角的两边分别交于 M、N 两点;
A
B
M
N
P
O
已知:∠AOB.
求作:∠AOB 的平分线.
仔细观察作图步骤
画一画
(3) 作射线 OP.
射线 OP 就是所要求作的∠AOB 的平分线.
(2) 分别以点 M 和 N 为圆心、相同长(大于线段 MN 长的一半)为半径作弧,在∠AOB 内,两弧相交于点 P;
轴对称图形对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格,且不能折叠,你还能比较准确的画出图形的对称轴吗?
3
1. 画出下面图形的对称轴,画完图后请思考下面的问题:
① 能总结你画对称轴的方法吗?
② 连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分.
合作探究
2. 如图,点 A 和点 A′ 关于某条直线成轴对称,你能画出这条直线吗?
A A′
(1) 找出图形的任意一组对称点;
画图形的对称轴的画法:
(2) 连结对称点;
(3) 画出对称点所连线段的垂直平分线.
就可以得到该图形的对称轴.
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
归纳总结
第肆章节
随堂练习
随堂练习
1.平面上的两条相交直线是轴对称图吗?如果是,它有几条对称轴?作图试试看.
解:是轴对称图形,对称轴有两条,是两直线夹角的平分线所在的直线(画图略).
【教材P120 练习 第1题】
2.把一张正方形纸对折两次,然后分别剪出下列图形.
解:(1)操作步骤如图①所示.
(2)操作步骤如图②所示.
【教材P120 练习 第2题】
3.图中的一些虚线,哪些是图形的对称轴,哪些不是?
②④⑥是图形的对称轴,①③⑤不是.
【教材P120 练习 第3题】
4.如图,已知△ABC ,利用尺规作图作出△ABC的边BC上的中线.
A
B
C
解:①作出线段BC的垂直平分线,交线段BC于点O;
②连接AO,线段AO即为△ABC的边BC 上的中线.
O
【教材P121 练习 第4题】
5.如图,已知△ABC ,利用尺规作图作出∠ABC的平分线.
A
B
C
O
【教材P121 练习 第5题】
第伍章节
课堂小结
课堂小结
线段和角
线段和角都是轴对称图形
尺规作图
轴对称的再认识
作轴对称图形的对称轴
如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
