9.1.3 作轴对称图形 课件(共27张PPT)
文档属性
| 名称 | 9.1.3 作轴对称图形 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 09:15:54 | ||
图片预览







文档简介
(共27张PPT)
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.1.3 作轴对称图形
9.1 轴对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能够按要求画简单平面图形经过一次对称后的图形.
2.掌握作轴对称图形的方法.
第贰章节
新课导入
新课导入
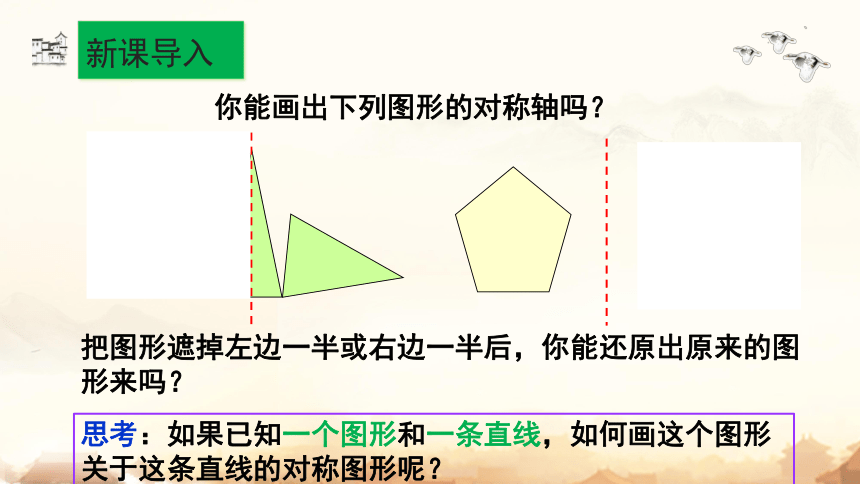
你能画出下列图形的对称轴吗?
思考:如果已知一个图形和一条直线,如何画这个图形关于这条直线的对称图形呢?
把图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
第叁章节
新知探究
新知探究
轴对称图形的画法
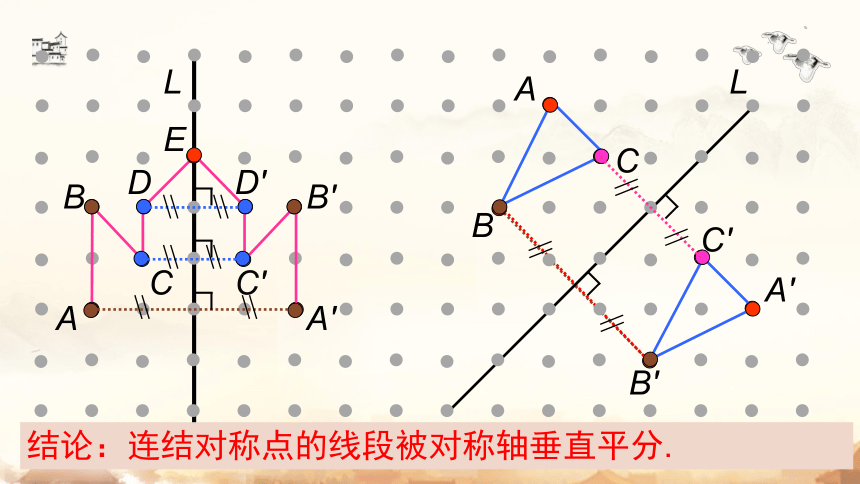
试一试:如图,实线所构成的图形为已知图形,虚线为对称轴,试作出已知图形的轴对称图形. 作好之后,你可以通过对折的方法来验证你作得是否正确.
E
A'
A
C'
C
A'
A
C
C'
D
D'
B
B'
B
B'
L
L
结论:连结对称点的线段被对称轴垂直平分.
由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线 l 的对称点;连结任意一对对称点的线段被对称轴垂直平分.
归纳总结
探究:如果没有格点,应如何作出某个图形的轴对称图形呢
思考:我们已经能利用尺规作图,作已知线段的垂直平分线,作已知角的平分线,那么如何利用尺规作图,过已知点作出已知直线的垂线,从而得到已知点关于已知直线的对称点呢
合作探究
(1) 经过已知直线 AB 上一点 C 作已知直线 AB 的垂线.
已知点与已知直线可以有两种不同的位置关系:
(1)点在直线上;(2)点在直线外.
现分别按这两种情况作图.
分析:如图,由于点 C 在直线 AB 上,因此所要求作的垂线正好是平角 ∠ACB 的平分线所在的直线.
A
B
C
l
1. 如图,经过已知直线 AB 上一点 C,试利用尺规作图,按下列作法准确地作出直线 AB 的垂线.
P
A
B
C
(1) 作平角∠ACB 的平分线 CP;
(2) 反向延长射线 CP.
直线 CP 就是所要求作的垂线.
画一画
(2) 经过已知直线 AB 外一点 C 作已知直线 AB 的垂线.
分析:如图,由于点 C 是垂线上的一个点,因此要作出垂线,只要再找到垂线上的另一点 P.
M
N
O
P
C
A
B
请归纳一下作图步骤.
A
B
C
P
2. 如图,经过已知直线 AB 外一点 C,试利用尺规作图,按下列作法准确地作出直线 AB 的垂线.
(1) 以点 C 为圆心、适当长(大于点 C到直线 AB 的距离)为半径作弧,交直线 AB 于 M、N 两点;
(2) 分别以点 M、N 为圆心,相同长(大于线段 MN 长的一半)为半径作弧,两弧相交于点 P;
(3) 作直线 CP.
直线 CP 就是所要求作的垂线.
M
N
例1 如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图 1)
(图 2)
(图 3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
想一想:如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢?
例 2 如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
A
B
C
分析:△ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线 l 的对称点,连结这些对称点,就能得到要画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点;
(3) 连结 A′B′,B′C′,C′A′,得到的△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C关于直线 l 的对称点 B′,C′;
A
B
C
A′
B′
C′
O
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连结这些对称点,就可以得到原图形的轴对称图形.
知识要点
第肆章节
随堂练习
随堂练习
1.在图中分别作出点A关于两条直线的对称点A′和A″.
解:如图所示.
【教材P124 练习 第1题】
2.作出如图所示图形关于直线l的对称图形.
解:如图所示.
【教材P124 练习 第2题】
3.如图,已知△ABC,利用尺规作图作出△ABC的边BC上的高.
解:如图所示,线段AO即为边BC上的高.
A
B
C
O
M
P
N
【教材P124 练习 第3题】
第伍章节
课堂小结
课堂小结
画轴对称图形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.1.3 作轴对称图形
9.1 轴对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能够按要求画简单平面图形经过一次对称后的图形.
2.掌握作轴对称图形的方法.
第贰章节
新课导入
新课导入
你能画出下列图形的对称轴吗?
思考:如果已知一个图形和一条直线,如何画这个图形关于这条直线的对称图形呢?
把图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
第叁章节
新知探究
新知探究
轴对称图形的画法
试一试:如图,实线所构成的图形为已知图形,虚线为对称轴,试作出已知图形的轴对称图形. 作好之后,你可以通过对折的方法来验证你作得是否正确.
E
A'
A
C'
C
A'
A
C
C'
D
D'
B
B'
B
B'
L
L
结论:连结对称点的线段被对称轴垂直平分.
由一个平面图形可以得到与它关于一条直线 l 对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线 l 的对称点;连结任意一对对称点的线段被对称轴垂直平分.
归纳总结
探究:如果没有格点,应如何作出某个图形的轴对称图形呢
思考:我们已经能利用尺规作图,作已知线段的垂直平分线,作已知角的平分线,那么如何利用尺规作图,过已知点作出已知直线的垂线,从而得到已知点关于已知直线的对称点呢
合作探究
(1) 经过已知直线 AB 上一点 C 作已知直线 AB 的垂线.
已知点与已知直线可以有两种不同的位置关系:
(1)点在直线上;(2)点在直线外.
现分别按这两种情况作图.
分析:如图,由于点 C 在直线 AB 上,因此所要求作的垂线正好是平角 ∠ACB 的平分线所在的直线.
A
B
C
l
1. 如图,经过已知直线 AB 上一点 C,试利用尺规作图,按下列作法准确地作出直线 AB 的垂线.
P
A
B
C
(1) 作平角∠ACB 的平分线 CP;
(2) 反向延长射线 CP.
直线 CP 就是所要求作的垂线.
画一画
(2) 经过已知直线 AB 外一点 C 作已知直线 AB 的垂线.
分析:如图,由于点 C 是垂线上的一个点,因此要作出垂线,只要再找到垂线上的另一点 P.
M
N
O
P
C
A
B
请归纳一下作图步骤.
A
B
C
P
2. 如图,经过已知直线 AB 外一点 C,试利用尺规作图,按下列作法准确地作出直线 AB 的垂线.
(1) 以点 C 为圆心、适当长(大于点 C到直线 AB 的距离)为半径作弧,交直线 AB 于 M、N 两点;
(2) 分别以点 M、N 为圆心,相同长(大于线段 MN 长的一半)为半径作弧,两弧相交于点 P;
(3) 作直线 CP.
直线 CP 就是所要求作的垂线.
M
N
例1 如何画一条线段的对称图形?
已知线段 AB,画出 AB 关于直线 l 的对称线段.
A
B
(图 1)
(图 2)
(图 3)
A
B
l
l
A
B
l
A′
A′
A′
B′
(B′)
B′
想一想:如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢?
例 2 如图,已知△ABC 和直线 l,作出与△ABC关于直线 l 对称的图形.
A
B
C
分析:△ABC 可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线 l 的对称点,连结这些对称点,就能得到要画的图形.
作法:(1) 过点 A 画直线 l 的垂线,垂足为点 O,在垂线上截取 OA′ = OA,A′ 就是点 A 关于直线 l 的对称点;
(3) 连结 A′B′,B′C′,C′A′,得到的△A′B′C′ 即为所求.
(2) 同理,分别画出点 B,C关于直线 l 的对称点 B′,C′;
A
B
C
A′
B′
C′
O
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连结这些对称点,就可以得到原图形的轴对称图形.
知识要点
第肆章节
随堂练习
随堂练习
1.在图中分别作出点A关于两条直线的对称点A′和A″.
解:如图所示.
【教材P124 练习 第1题】
2.作出如图所示图形关于直线l的对称图形.
解:如图所示.
【教材P124 练习 第2题】
3.如图,已知△ABC,利用尺规作图作出△ABC的边BC上的高.
解:如图所示,线段AO即为边BC上的高.
A
B
C
O
M
P
N
【教材P124 练习 第3题】
第伍章节
课堂小结
课堂小结
画轴对称图形
作图原理
作图方法
对称轴是对称点连线段的垂直平分线.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
