9.4 中心对称 课件(共31张PPT)
文档属性
| 名称 | 9.4 中心对称 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 09:22:26 | ||
图片预览








文档简介
(共31张PPT)
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.4 中心对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解成中心对称的两个图形与中心对称图形的概念,并且
知道两者之间的区别与联系.
2.掌握它们的性质,会判断两个图形是否成中心对称.
3.会画一个图形关于一个点成中心对称的图形.
第贰章节
新课导入
新课导入
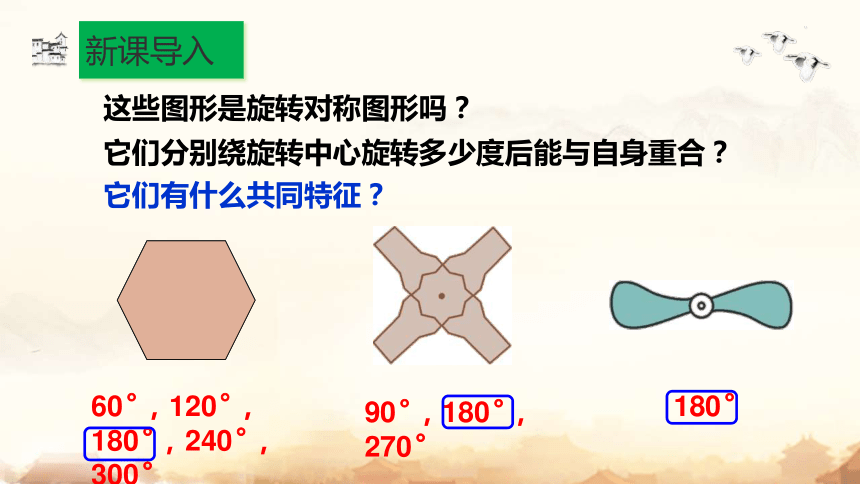
这些图形是旋转对称图形吗?
它们分别绕旋转中心旋转多少度后能与自身重合?
60°,120°,180°,240°,300°
90°,180°,270°
180°
它们有什么共同特征?
第叁章节
新知探究
新知探究
中心对称的概念
(1) 线段
(2) 花瓣
A
B
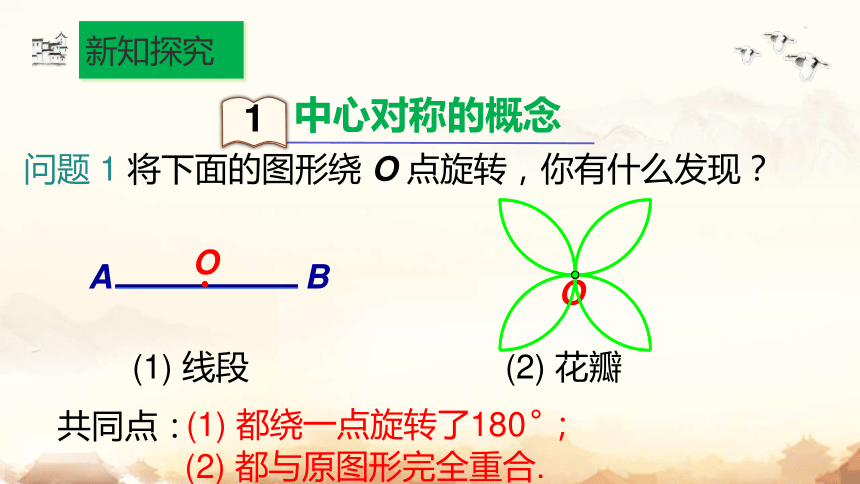
问题 1 将下面的图形绕 O 点旋转,你有什么发现?
O
O
共同点:
(1) 都绕一点旋转了180°;
(2) 都与原图形完全重合.
1
上题中的一个图形绕着中心旋转 180°,后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
知识要点
中心对称图形是旋转角度为180° 的旋转对称图形.
花瓣
O
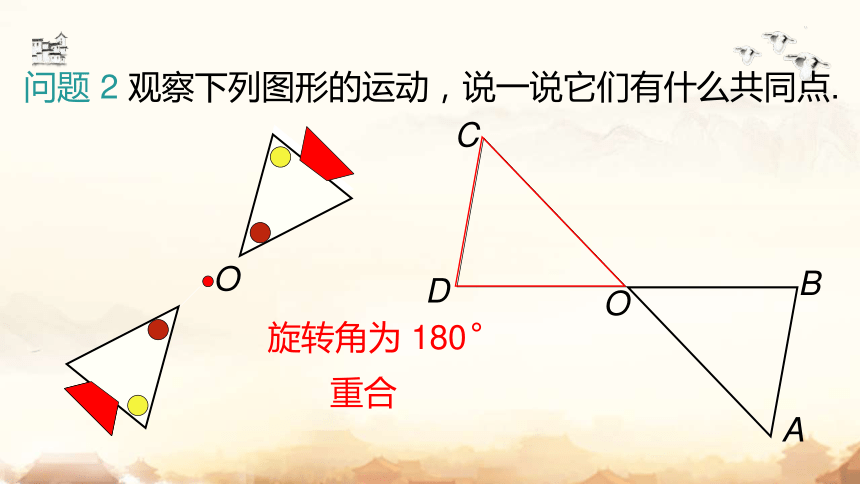
重合
O
A
D
B
C
问题 2 观察下列图形的运动,说一说它们有什么共同点.
旋转角为 180°
O
把一个图形绕着某一点旋转 180°,如果它能够和另外一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
知识要点
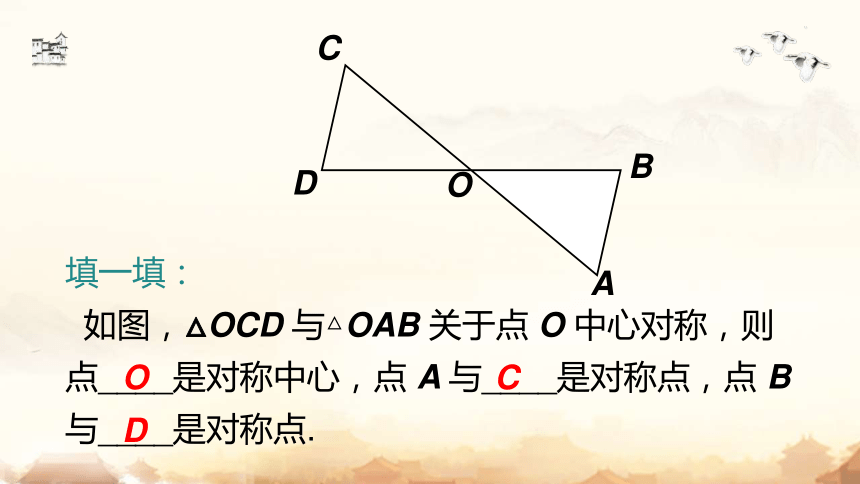
填一填:
如图,△OCD 与△OAB 关于点 O 中心对称,则点____是对称中心,点 A 与____是对称点,点 B 与____是对称点.
O
B
C
A
D
O
C
D
1. 中心对称是一种特殊的旋转,其旋转角是 180°;
2. 中心对称是两个图形之间一种特殊的位置关系.
归纳总结
中心对称的性质
如图,旋转三角尺,
画出△ABC 关于
点 O 中心
对称的△A′B′C′.
A′
C
A
B
B′
C′
O
●
2
(1) A、O、A' 三点共线;
B、O、B'三点共线;
C、O、C' 三点共线.
(2) OA = OA′、OB = OB′、OC = OC′.
找一找:
下图中△A′B′C′ 与△ABC 关于点 O 成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
中心对称的基本性质
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
知识要点
例 如图,选择点 O 为对称中心,画出与△ABC 关于点 O 成中心对称的△A′B′C′.
A′
C′
B′
△A′B′C′ 为所求作的三角形.
B
A
C
O
典例精析
练一练:如图,已知 △ABC 与 △A′B′C′ 成中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′ 应是对应点,连结 BB′,用刻度尺找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连结 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,我们用解法 2.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
拓展提升
中心对称与轴对称的异同
第肆章节
随堂练习
随堂练习
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEM
TUVWY
HIOX
HINOSXZ
HINOSXZ
【教材P150 练习 第1题】
2.如图,四边形ABCD是长方形,AB>BC.这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
A
B
C
D
解:如图,这个长方形是轴对称图形,有两条对称轴;
是中心对称图形,它的对称中心是两条对角线的交点;
是旋转对称图形,绕对称中心旋转180°后能与自身重合.
【教材P151 练习 第2题】
3.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师摘除蒙具后,看到4张扑克牌如图②所示,他很快确定了哪一张牌被旋转过.你能确定吗?
解:被旋转180°的那张牌是方块4.
①
②
【教材P151 练习 第3题】
4.如图,已知四边形 ABCD 和点O,作四边形 A′B′C′D′,使四边形 A′B′C′D′ 和四边形ABCD 关于点 O 成中心对称.
A
B
C
D
A′
B′
C′
D′
O
【教材P153 练习 第1题】
5.如图,已知点P是△ABC内一点,作出△ABC关于点P成中心对称的△A′B′C′.
A
B
C
P
A′
B′
C′
【教材P153 练习 第2题】
6.如图,先在纸上作△ABC和点P,再作出△ABC关于点P成中心对称的△A′B′C′.在此基础上,再过点P任意作一条直线,作出△ABC 关于此直线对称的△A″B″C″.观察△A′B′C′和△A″B″C″,你发现了什么?
解:过点P作直线的垂线, △A′B′C′和△A″B″C″关于这条垂线对称.
【教材P153 练习 第3题】
第伍章节
课堂小结
课堂小结
中心对称
概念
图形绕着中心旋转 180° 后能与自身重合
性质
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.4 中心对称
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解成中心对称的两个图形与中心对称图形的概念,并且
知道两者之间的区别与联系.
2.掌握它们的性质,会判断两个图形是否成中心对称.
3.会画一个图形关于一个点成中心对称的图形.
第贰章节
新课导入
新课导入
这些图形是旋转对称图形吗?
它们分别绕旋转中心旋转多少度后能与自身重合?
60°,120°,180°,240°,300°
90°,180°,270°
180°
它们有什么共同特征?
第叁章节
新知探究
新知探究
中心对称的概念
(1) 线段
(2) 花瓣
A
B
问题 1 将下面的图形绕 O 点旋转,你有什么发现?
O
O
共同点:
(1) 都绕一点旋转了180°;
(2) 都与原图形完全重合.
1
上题中的一个图形绕着中心旋转 180°,后能与自身重合,我们把这种图形叫做中心对称图形,这个中心叫做对称中心.
知识要点
中心对称图形是旋转角度为180° 的旋转对称图形.
花瓣
O
重合
O
A
D
B
C
问题 2 观察下列图形的运动,说一说它们有什么共同点.
旋转角为 180°
O
把一个图形绕着某一点旋转 180°,如果它能够和另外一个图形重合,那么,我们就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点,叫做关于中心的对称点.
知识要点
填一填:
如图,△OCD 与△OAB 关于点 O 中心对称,则点____是对称中心,点 A 与____是对称点,点 B 与____是对称点.
O
B
C
A
D
O
C
D
1. 中心对称是一种特殊的旋转,其旋转角是 180°;
2. 中心对称是两个图形之间一种特殊的位置关系.
归纳总结
中心对称的性质
如图,旋转三角尺,
画出△ABC 关于
点 O 中心
对称的△A′B′C′.
A′
C
A
B
B′
C′
O
●
2
(1) A、O、A' 三点共线;
B、O、B'三点共线;
C、O、C' 三点共线.
(2) OA = OA′、OB = OB′、OC = OC′.
找一找:
下图中△A′B′C′ 与△ABC 关于点 O 成中心对称,你能从图中找到哪些等量关系
A′
B′
C′
A
B
C
O
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
中心对称的基本性质
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
知识要点
例 如图,选择点 O 为对称中心,画出与△ABC 关于点 O 成中心对称的△A′B′C′.
A′
C′
B′
△A′B′C′ 为所求作的三角形.
B
A
C
O
典例精析
练一练:如图,已知 △ABC 与 △A′B′C′ 成中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′ 应是对应点,连结 BB′,用刻度尺找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连结 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,我们用解法 2.
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
拓展提升
中心对称与轴对称的异同
第肆章节
随堂练习
随堂练习
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
轴对称 旋转对称 中心对称
只有一条对称轴 有两条对称轴 英文字母
ABCDEM
TUVWY
HIOX
HINOSXZ
HINOSXZ
【教材P150 练习 第1题】
2.如图,四边形ABCD是长方形,AB>BC.这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
A
B
C
D
解:如图,这个长方形是轴对称图形,有两条对称轴;
是中心对称图形,它的对称中心是两条对角线的交点;
是旋转对称图形,绕对称中心旋转180°后能与自身重合.
【教材P151 练习 第2题】
3.如图①所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°,魔术师摘除蒙具后,看到4张扑克牌如图②所示,他很快确定了哪一张牌被旋转过.你能确定吗?
解:被旋转180°的那张牌是方块4.
①
②
【教材P151 练习 第3题】
4.如图,已知四边形 ABCD 和点O,作四边形 A′B′C′D′,使四边形 A′B′C′D′ 和四边形ABCD 关于点 O 成中心对称.
A
B
C
D
A′
B′
C′
D′
O
【教材P153 练习 第1题】
5.如图,已知点P是△ABC内一点,作出△ABC关于点P成中心对称的△A′B′C′.
A
B
C
P
A′
B′
C′
【教材P153 练习 第2题】
6.如图,先在纸上作△ABC和点P,再作出△ABC关于点P成中心对称的△A′B′C′.在此基础上,再过点P任意作一条直线,作出△ABC 关于此直线对称的△A″B″C″.观察△A′B′C′和△A″B″C″,你发现了什么?
解:过点P作直线的垂线, △A′B′C′和△A″B″C″关于这条垂线对称.
【教材P153 练习 第3题】
第伍章节
课堂小结
课堂小结
中心对称
概念
图形绕着中心旋转 180° 后能与自身重合
性质
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分
作图
应用1:作中心对称图形;
应用2:找出对称中心.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
