9.5 图形的全等 课件(共25张PPT)
文档属性
| 名称 | 9.5 图形的全等 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 09:22:59 | ||
图片预览







文档简介
(共25张PPT)
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.5 图形的全等
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.了解全等图形、全等多边形、全等三角形的定义.
2.探究全等多边形和全等三角形的性质与判定.
3.体会图形的三种变换与图形全等的关系.
第贰章节
新课导入
新课导入
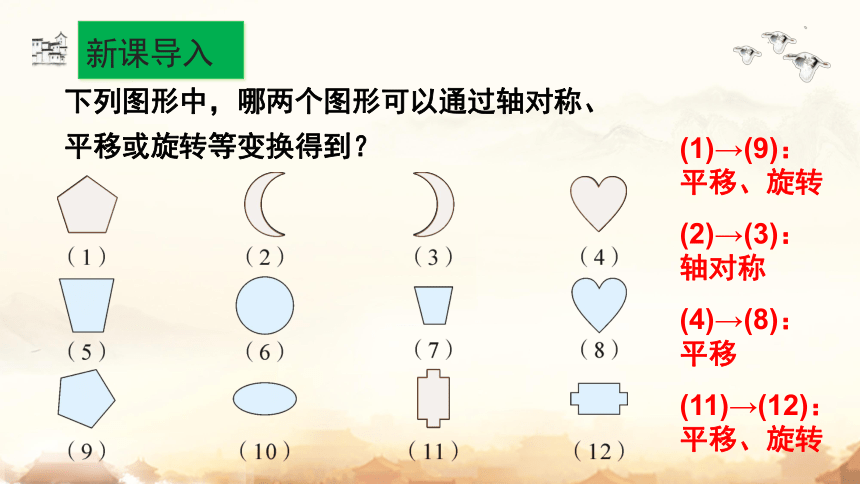
下列图形中,哪两个图形可以通过轴对称、平移或旋转等变换得到?
(1)→(9):
平移、旋转
(2)→(3):
轴对称
(4)→(8):
平移
(11)→(12):
平移、旋转
观察思考:每组中的两个图形有什么特点?
图形经过变换后,位置______,形状______,大小______.
也就是说,变换前后两个图形对应位置的线段______,对应位置的角______.
变换前后的两个图形能够完全重合吗?
改变
不变
不变
相等
相等
第叁章节
新知探究
新知探究
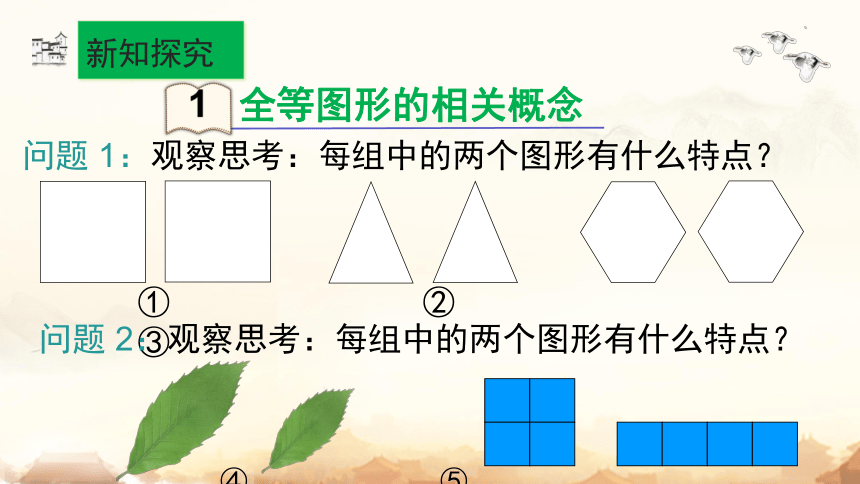
全等图形的相关概念
问题 1:观察思考:每组中的两个图形有什么特点?
① ② ③
问题 2:观察思考:每组中的两个图形有什么特点?
④ ⑤
1
全等图形的定义:
能够完全重合的两个图形称为全等图形.
知识要点
问题:如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同.
想一想:观察下面两组图形,它们是不是全等图形 为什么 与同伴进行交流.
两个图形形状相同,但大小不同.
两个图形面积相同,但形状不同.
它们不能完全重合,不是全等图形
注意:全等图形的特征是完全重合.
1. 两个能够完全重合的图形称为全等图形.
2. 图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3. 两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
知识要点
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,
相互重合的角叫做对应角.
A
B
C
D
E
A1
B1
C1
D1
E1
五边形 ABCDE≌五边形 A1B1C1D1E1
对应边
试一试:找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A = ∠A1
∠B =∠B1
∠D = ∠D1
∠E ∠E1
=
∠C =∠C1
此符号表示全等,读作“全等于”.
全等图形的性质
2
全等多边形的性质:
全等多边形的对应边相等,对应角相等.
全等多边形的判定方法:
边、角分别对应相等的两个多边形称为全等多边形.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
知识要点
练一练:
如果△ABC≌△DEF,那么你可以得到:
∠A =∠D,∠B =∠E,∠C =∠F.
A
B
C
D
E
F
AB = DE,BC = EF,AC = DF;
由图形平移的特征,可知 △ABC 与△DEF 能够完全重合,即
△ABC≌△DEF.
∴ ∠D =∠A = 80°,
同理∠DEF = ∠B = 60°.
又∵ ∠D +∠DEF +∠F = 180°,
∴ ∠F = 180° -∠D -∠DEF = 40°.
A
B
C
D
E
F
例 如图,△ABC 沿着 BC 的方向平移至 △DEF,∠A = 80°, ∠B = 60°,求 ∠F 的度数.
解:
典例精析
第肆章节
随堂练习
随堂练习
1. 在日常生活中,处处可以看到全等的图形,例如同一张底片印出的同样尺寸的照片、我们使用的数学教科书的封面、我们班的课桌面等. 试尽可能多地举出生活中全等图形的例子,和同学比一比,看谁举出的例子多.
解:生活中全等的图形有很多,如同学们使用的语文教材的封面、各个教室里统一装配的同一型号尺寸的黑板面、铺设地面时用的同一类型大小相同的瓷砖等(答案不唯一).
【教材P160练习 第1题】
2. 如图,△ABD 绕着点A逆时针旋转 60°到
△ACE 位置,则△_____≌△ _____,这两个
三角形的对应点是___与___, ___与___, ___与___;
对应边是____与____, ____与____, ____与____;
对应角是_______与_______, _______与_______, _______与_______;∠BAC =∠_____= _____°.
ABD
【教材P160练习 第2题】
A
B
C
D
E
ACE
A
A
B
C
D
E
AB
AC
AD
AE
BD
CE
∠BAD
∠CAE
∠ABD
∠ACE
∠BDA
∠CEA
DAE
60
3.如图,点 E 是正方形 ABCD 的边 AB 上的一点,△ADE 绕着点 D 逆时针旋转到△CDF 位置,则△_____≌△ _____,这两个三角形的对应边是____与____, ____与____, ____与____;对应角是_______与_______, _______与_______, _______与_______;由于∠_____= _____°,因此上述旋转的旋转角度等于______°.
【教材P161练习 第3题】
A
B
C
D
E
F
ADE
CDF
AD
CD
AE
CF
DE
DF
∠A
∠DCF
∠ADE
∠CDF
∠AED
∠F
ADC
90
90
4. 如图,已知∠ABD = 110°,∠C = 45°,△ABC 与 △BAD 关于直线 l 成轴对称,则△ABC ≌ △ _______,∠BAD = _______°,∠AEC = ______°.
BAD
25
50
【教材P161练习 第4题】
A
B
C
D
E
l
第伍章节
课堂小结
课堂小结
全等图形
概念
能够完全重合的两个图形叫做全等图形
性质
对应角相等,对应边相等
如果两个三角形的边、角分别对应相等,那么这两个三角形全等
全等多边形
全等三角形
概念
判定
性质
判定
对应角相等,对应边相等
两对多边形都是全等图形,也叫做全等多边形
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
华东师大版数学七年级下册
第9章 轴对称、平移与旋转
汇报人:孙老师
汇报班级:X级X班
9.5 图形的全等
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.了解全等图形、全等多边形、全等三角形的定义.
2.探究全等多边形和全等三角形的性质与判定.
3.体会图形的三种变换与图形全等的关系.
第贰章节
新课导入
新课导入
下列图形中,哪两个图形可以通过轴对称、平移或旋转等变换得到?
(1)→(9):
平移、旋转
(2)→(3):
轴对称
(4)→(8):
平移
(11)→(12):
平移、旋转
观察思考:每组中的两个图形有什么特点?
图形经过变换后,位置______,形状______,大小______.
也就是说,变换前后两个图形对应位置的线段______,对应位置的角______.
变换前后的两个图形能够完全重合吗?
改变
不变
不变
相等
相等
第叁章节
新知探究
新知探究
全等图形的相关概念
问题 1:观察思考:每组中的两个图形有什么特点?
① ② ③
问题 2:观察思考:每组中的两个图形有什么特点?
④ ⑤
1
全等图形的定义:
能够完全重合的两个图形称为全等图形.
知识要点
问题:如果两个图形全等,它们的形状与大小一定相同吗?
全等图形的形状与大小都相同.
想一想:观察下面两组图形,它们是不是全等图形 为什么 与同伴进行交流.
两个图形形状相同,但大小不同.
两个图形面积相同,但形状不同.
它们不能完全重合,不是全等图形
注意:全等图形的特征是完全重合.
1. 两个能够完全重合的图形称为全等图形.
2. 图形经过轴对称、平移或旋转等变换所得到的新图形一定与原图形全等.
3. 两个全等图形经过轴对称、平移或旋转等变换后一定能够互相重合.
知识要点
思考:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?
概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,
相互重合的角叫做对应角.
A
B
C
D
E
A1
B1
C1
D1
E1
五边形 ABCDE≌五边形 A1B1C1D1E1
对应边
试一试:找出下面全等多边形的等量关系
AB A1B1
BC B1C1
CD C1D1
DE D1E1
EA E1A1
=
=
=
=
=
对应角
∠A = ∠A1
∠B =∠B1
∠D = ∠D1
∠E ∠E1
=
∠C =∠C1
此符号表示全等,读作“全等于”.
全等图形的性质
2
全等多边形的性质:
全等多边形的对应边相等,对应角相等.
全等多边形的判定方法:
边、角分别对应相等的两个多边形称为全等多边形.
全等三角形的性质:
全等三角形的对应边、对应角分别相等.
全等三角形的判定方法:
如果两个三角形的边、角分别对应相等,那么这两个三角形全等.
知识要点
练一练:
如果△ABC≌△DEF,那么你可以得到:
∠A =∠D,∠B =∠E,∠C =∠F.
A
B
C
D
E
F
AB = DE,BC = EF,AC = DF;
由图形平移的特征,可知 △ABC 与△DEF 能够完全重合,即
△ABC≌△DEF.
∴ ∠D =∠A = 80°,
同理∠DEF = ∠B = 60°.
又∵ ∠D +∠DEF +∠F = 180°,
∴ ∠F = 180° -∠D -∠DEF = 40°.
A
B
C
D
E
F
例 如图,△ABC 沿着 BC 的方向平移至 △DEF,∠A = 80°, ∠B = 60°,求 ∠F 的度数.
解:
典例精析
第肆章节
随堂练习
随堂练习
1. 在日常生活中,处处可以看到全等的图形,例如同一张底片印出的同样尺寸的照片、我们使用的数学教科书的封面、我们班的课桌面等. 试尽可能多地举出生活中全等图形的例子,和同学比一比,看谁举出的例子多.
解:生活中全等的图形有很多,如同学们使用的语文教材的封面、各个教室里统一装配的同一型号尺寸的黑板面、铺设地面时用的同一类型大小相同的瓷砖等(答案不唯一).
【教材P160练习 第1题】
2. 如图,△ABD 绕着点A逆时针旋转 60°到
△ACE 位置,则△_____≌△ _____,这两个
三角形的对应点是___与___, ___与___, ___与___;
对应边是____与____, ____与____, ____与____;
对应角是_______与_______, _______与_______, _______与_______;∠BAC =∠_____= _____°.
ABD
【教材P160练习 第2题】
A
B
C
D
E
ACE
A
A
B
C
D
E
AB
AC
AD
AE
BD
CE
∠BAD
∠CAE
∠ABD
∠ACE
∠BDA
∠CEA
DAE
60
3.如图,点 E 是正方形 ABCD 的边 AB 上的一点,△ADE 绕着点 D 逆时针旋转到△CDF 位置,则△_____≌△ _____,这两个三角形的对应边是____与____, ____与____, ____与____;对应角是_______与_______, _______与_______, _______与_______;由于∠_____= _____°,因此上述旋转的旋转角度等于______°.
【教材P161练习 第3题】
A
B
C
D
E
F
ADE
CDF
AD
CD
AE
CF
DE
DF
∠A
∠DCF
∠ADE
∠CDF
∠AED
∠F
ADC
90
90
4. 如图,已知∠ABD = 110°,∠C = 45°,△ABC 与 △BAD 关于直线 l 成轴对称,则△ABC ≌ △ _______,∠BAD = _______°,∠AEC = ______°.
BAD
25
50
【教材P161练习 第4题】
A
B
C
D
E
l
第伍章节
课堂小结
课堂小结
全等图形
概念
能够完全重合的两个图形叫做全等图形
性质
对应角相等,对应边相等
如果两个三角形的边、角分别对应相等,那么这两个三角形全等
全等多边形
全等三角形
概念
判定
性质
判定
对应角相等,对应边相等
两对多边形都是全等图形,也叫做全等多边形
如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
华东师大版数学七年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
