(人教版)五年级数学下册期末真题汇编——解答题(70题)(含解析)
文档属性
| 名称 | (人教版)五年级数学下册期末真题汇编——解答题(70题)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 07:37:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
(人教版)五年级数学下册期末真题汇编——解答题 (70题)
1.(23-24五年级下·江西九江·期末)5月25日至26日,“庐山杯”长江经济带龙舟邀请赛在九江市南门湖举行。一共有37支代表队参赛,其中大龙舟有21支代表队,小龙舟有16支代表队。大龙舟代表队的参赛支数是参赛代表队总支数的几分之几?
2.(23-24五年级下·重庆忠县·期末)如下图,小美从家到学校有两条路,一条经过公园,另一条经过邮局。走哪条比较近?
3.(2024·湖北荆州·小升初真题)只列式,不计算。
某工厂要加工32000个零件。甲生产线单独做16天完成;乙生产线单独做20天完成。如果两组生产线合做,几天可以完成?
4.(2024·浙江杭州·小升初真题)有一张长方形纸板,长80厘米,宽60厘米,如果要剪成若干同样大小的正方形而没有剩余,剪出小正方形的边长最大是多少厘米?可以剪多少个这样的小正方形?
5.(23-24五年级下·河北唐山·期末)一节数学课时长小时。老师讲解的时间占,学生小组探究的时间占,剩下的是学生独立做练习的时间。做练习的时间占整节课的几分之几?
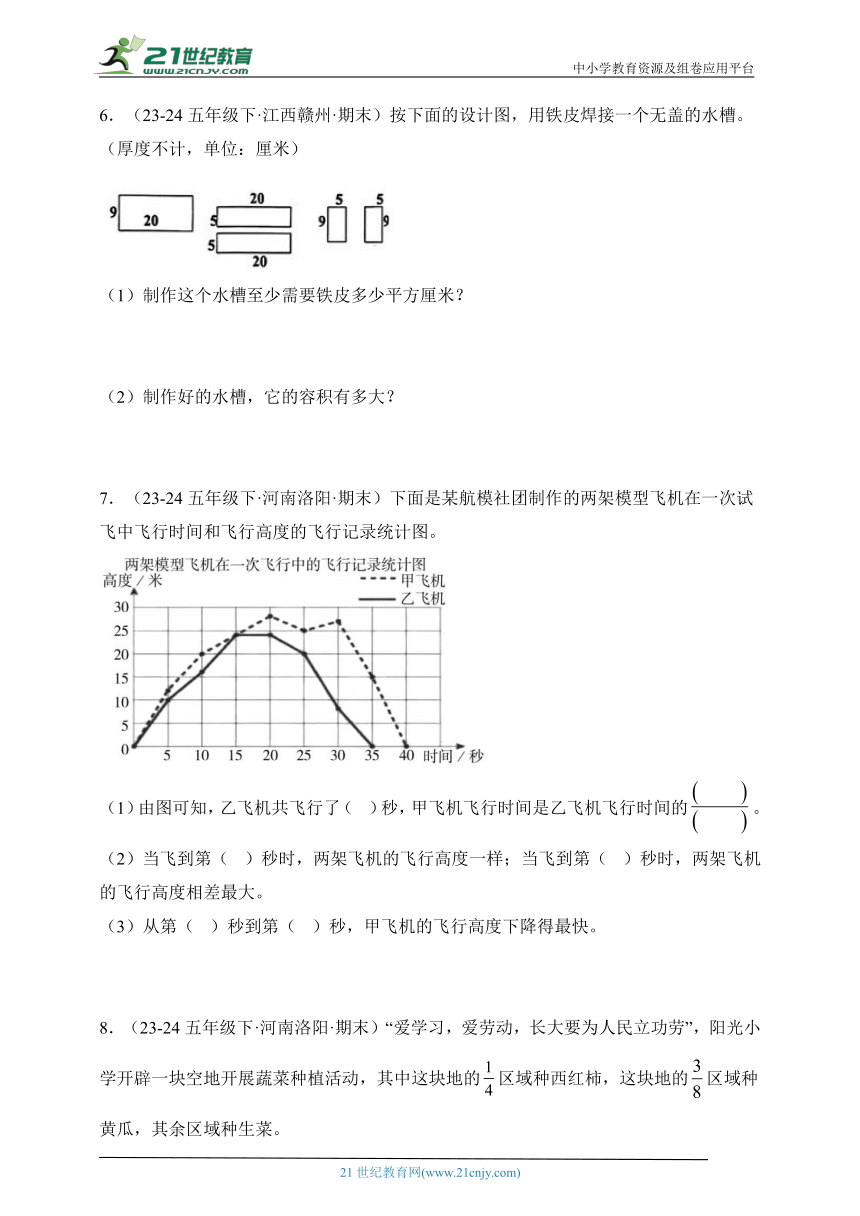
6.(23-24五年级下·江西赣州·期末)按下面的设计图,用铁皮焊接一个无盖的水槽。(厚度不计,单位:厘米)
(1)制作这个水槽至少需要铁皮多少平方厘米?
(2)制作好的水槽,它的容积有多大?
7.(23-24五年级下·河南洛阳·期末)下面是某航模社团制作的两架模型飞机在一次试飞中飞行时间和飞行高度的飞行记录统计图。
(1)由图可知,乙飞机共飞行了( )秒,甲飞机飞行时间是乙飞机飞行时间的。
(2)当飞到第( )秒时,两架飞机的飞行高度一样;当飞到第( )秒时,两架飞机的飞行高度相差最大。
(3)从第( )秒到第( )秒,甲飞机的飞行高度下降得最快。
8.(23-24五年级下·河南洛阳·期末)“爱学习,爱劳动,长大要为人民立功劳”,阳光小学开辟一块空地开展蔬菜种植活动,其中这块地的区域种西红柿,这块地的区域种黄瓜,其余区域种生菜。
(1)请在图中用斜线表示出种黄瓜的区域。
(2)算式要解决的问题是( )。
(3)种生菜区域比种西红柿区域多占这块地的几分之几?
9.(23-24五年级下·河南洛阳·期末)笑笑、乐乐、洛洛和阳阳四人学习了有趣的测量后,张老师让他们尝试测量一个不规则物体的体积,他们进行的实验步骤如下:
①笑笑准备了一个长和宽都是8厘米,高是15厘米的长方体玻璃缸;
②乐乐往缸里倒入一些水,此时水面距离玻璃缸口5厘米;
③洛洛把一个红薯完全浸没入水中,此时水面高度是14立方厘米;
④阳阳把红薯取出,这时水面高度是10厘米。
你能根据以上信息,计算这个红薯的体积是多少吗?
10.(23-24五年级下·河南安阳·期末)4月21日安阳市举办了甲骨文马拉松比赛。比赛分为全程马拉松、半程马拉松和欢乐跑三个项目,其中参加全程马拉松的人占总人数的,参加欢乐跑的人占总人数的,其他的是参加半程马拉松的人,参加半程马拉松的人占总人数的几分之几?
11.(23-24五年级下·河南安阳·期末)这是文创商店调查的200名顾客最喜欢的商品项目统计表。
最喜欢的文创商品 冰箱贴 抱枕 钥匙扣 水杯 其他
占总人数的几分之几
(1)最喜欢冰箱贴和抱枕的人数共占总人数的几分之几?
(2)最喜欢钥匙扣的比水杯的人数多占总人数的几分之几?
(3)请你提出一个数学问题并解答。
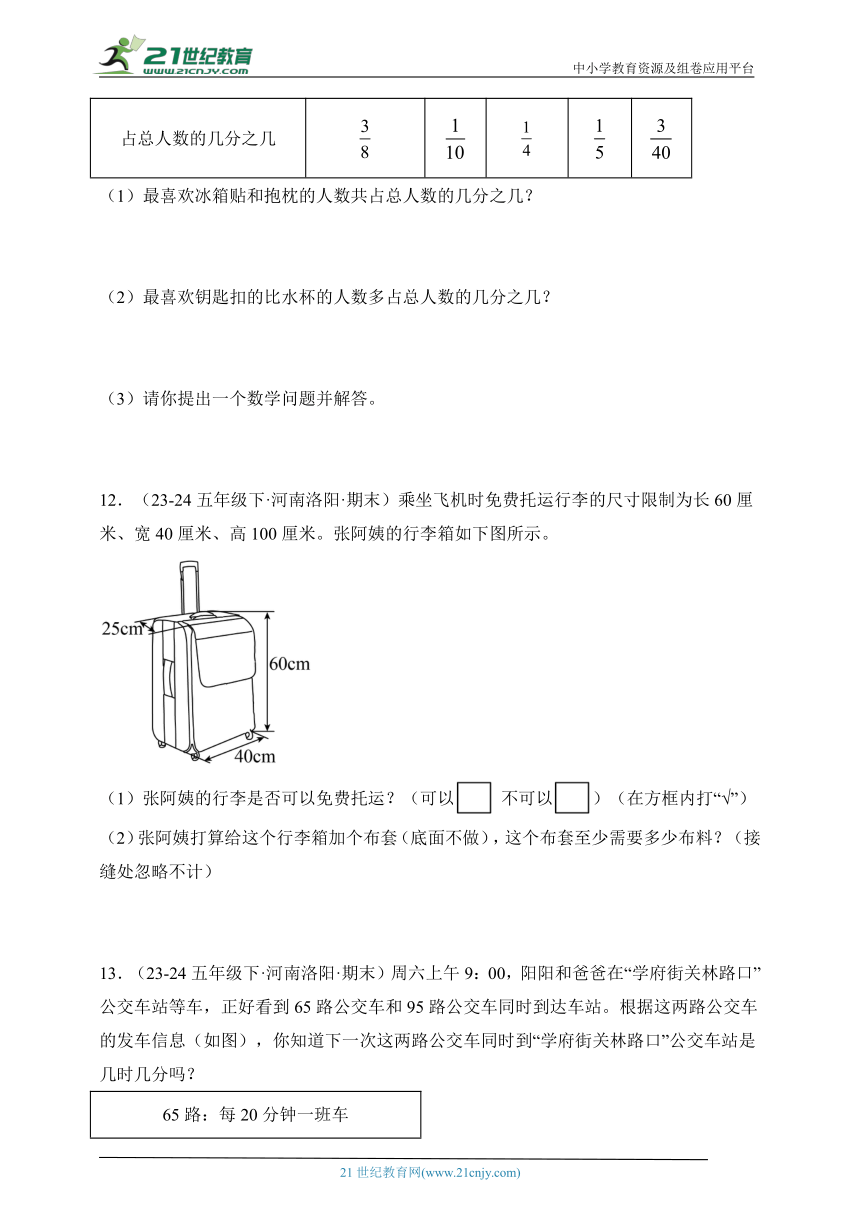
12.(23-24五年级下·河南洛阳·期末)乘坐飞机时免费托运行李的尺寸限制为长60厘米、宽40厘米、高100厘米。张阿姨的行李箱如下图所示。
(1)张阿姨的行李是否可以免费托运?(可以 不可以)(在方框内打“√”)
(2)张阿姨打算给这个行李箱加个布套(底面不做),这个布套至少需要多少布料?(接缝处忽略不计)
13.(23-24五年级下·河南洛阳·期末)周六上午9:00,阳阳和爸爸在“学府街关林路口”公交车站等车,正好看到65路公交车和95路公交车同时到达车站。根据这两路公交车的发车信息(如图),你知道下一次这两路公交车同时到“学府街关林路口”公交车站是几时几分吗?
65路:每20分钟一班车95路:每25分钟一班车
14.(23-24五年级下·江西九江·期末)2024年4月23日是第29个世界读书日,希望小学开展“读书节”的活动,图书馆每天都对外开放,欢迎每位学生都来图书馆阅读、借书。
(1)聪聪选了一本《趣味科学》,共280页,第一天看了全书的,第二天看了全书的,还剩这本书的几分之几没有看?
(2)睿睿和敏敏两人都在图书馆借书,睿睿每3天去一次,敏敏每5天去一次。如果5月8日他们两人在图书馆相遇,那么他们下次在图书馆相遇是几月几日?
15.(23-24五年级下·江西九江·期末)为了保护书籍,王老师打算用硬纸板为某套图书做一个封套(如下图),至少需要多少平方厘米的硬纸板?(硬纸板的厚度及接缝处忽略不计。)
16.(23-24五年级下·重庆九龙坡·期末)国家游泳中心又名“水立方”,在2022年北京冬奥会变身为“冰立方”,成为国际首个泳池上架设冰壶赛道的“双奥场馆”。
(1)在“水立方”游泳池的四壁和底面贴瓷片,贴瓷片的面积至少是多少平方米?
(2)“冰立方”内有4条冰壶赛道,一共需要用冰大约多少立方米?
17.(23-24五年级下·重庆忠县·期末)“嫦娥五号”在闯过地月转移、近月制动、环月飞行、月面着陆、自动采样、月面起飞、月轨交会对接、再入返回等多个难关后,成功携带月球样品返回地球。月球土壤成分中,氧占,硅占,铁占。除氧、硅、铁外,其它成分占月球土壤成分的几分之几?
18.(23-24五年级下·河南安阳·期末)明明买了一个亚当牛尊的工艺品,想知道它的体积是多少。明明把它放入一个长65厘米,宽40厘米,水深12厘米的容器中,结果水面升高到15厘米(水没有溢出)。你知道亚当牛尊工艺品的体积是多少立方厘米吗?
19.(23-24五年级下·江西九江·期末)小军的爸爸买了一个珊瑚,他把珊瑚放进鱼缸后,鱼缸内的水上升了10厘米,珊瑚的体积是多少立方厘米?
20.(23-24五年级下·江西吉安·期末)下面是贝贝比较土豆和红薯的体积时做的实验。(单位:厘米)
分别计算土豆和红薯的体积。
21.(23-24五年级下·河北唐山·期末)如图,花花用一张长30厘米、宽24厘米的长方形纸板,从四角各切掉一个边长6厘米的正方形,然后做成无盖盒子。
(1)如果在盒子外面贴上彩纸,贴彩纸的面积是多少平方厘米?
(2)这个盒子的容积是多少立方厘米?
22.(23-24五年级下·河南安阳·期末)殷墟博物馆新馆主体南侧有两个长90米、宽24米,深20厘米的水池。要往这两个水池中注满水,需要注入多少立方米的水?
23.(23-24五年级下·河南安阳·期末)博物馆里有许多保护文物的透明展示罩(无底),下图所示:这是其中一个,长是2米,宽0.6米,高0.8米,制作一个这样透明展示罩需要多少平方米的材料?
24.(23-24五年级下·河南安阳·期末)殷墟博物馆设有基本陈列馆、专题展览馆和特色沉浸式数字展。小明参观基本陈列馆用小时,参观专题展览馆用了小时,参观特色沉浸式数字展用小时,小明参观这三个馆一共用了多长时间?
25.(23-24五年级下·重庆忠县·期末)如下图是一个无盖长方体纸盒展开图,其中①,⑤为正方形。每平方米纸50元,做这个纸盒至少需要多少元?
26.(23-24五年级下·四川绵阳·期末)工程队修一条1500米长的路,第一周修了500米,第二周修了这条路的。工程队第一周修了这条路的几分之几?两周后这条路还剩几分之几没有修?
27.(23-24五年级下·四川绵阳·期末)用一根铁丝刚好焊成一个棱长10厘米的正方体框架,如果把它改成一个长14厘米,宽8厘米的长方体框架。长方体框架的高是多少厘米?
28.(23-24五年级下·四川绵阳·期末)在下图的玻璃鱼缸中放入一块高1.5分米、体积为6立方分米的假山石。如果水管以每分钟10立方分米的流量向鱼缸内注水,至少需要多长时间才能把假山石刚好淹没?
29.(23-24五年级下·四川南充·期末)某食堂仓库储存了吨大米,比储存的小米多吨;储存的面粉比储存的小米多0.4吨。这个仓库储存了多少吨面粉?
30.(23-24五年级下·四川南充·期末)有一个底面为正方形的长方体纸箱,下图是它的六个面中的两个面,请你根据相关数据,计算出这个长方体的表面积(连接处材料不计)。
31.(23-24五年级下·四川南充·期末)一个长方体玻璃水缸,长8分米,宽5分米,高5分米,水深4分米。如果竖直放入一块棱长为4分米的正方体铁块,缸里的水会溢出多少升?
32.(23-24五年级下·四川南充·期末)五(2)班要在小林和小丽两位同学中,选出一名同学代表班级参加学校举行的跳绳比赛。下面是他们一周每天一分钟跳绳的情况记录,请根据图中信息解决下列问题。
(1)从图中可以看出,小林同学一分钟跳绳的最高成绩与最低成绩相差( )个;小丽同学一分钟跳绳的最高成绩与最低成绩相差( )个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现( )趋势。(填“上升”或“下降”)
(3)你会推荐哪位同学代表班级参加一分钟跳绳比赛?说说你的理由。
33.(23-24五年级下·四川南充·期末)某超市有96箱矿泉水,第一天卖了12箱,第二天卖了20箱。两天一共卖了所有矿泉水的几分之几?
34.(23-24五年级下·四川南充·期末)五(1)班到罗瑞卿纪念馆开展研学活动。全程用时3小时,其中往返路上用去的时间占总时间的,休息的时间占总时间的,剩下的是参观学习时间。参观学习时间占总时间的几分之几?
35.(23-24五年级下·四川南充·期末)某科技公司研发出了A、B两款智能扫地机器人,并对其进行了六天的试验(实验条件完全相同),下面是根据它们试验期间的清扫时长制成的折线统计图。
(1)试验第( )天,两款扫地机器人的清扫时长相同。
(2)试验第( )天,两款扫地机器人的清扫时长相差最大,相差( )分钟。
(3)如果两款扫地机器人清扫效果大致相同,该公司会批量生产哪一款?请说明。
36.(23-24五年级下·四川南充·期末)在“美丽中国行,我是行动者”生态环保主题绘画比赛中,实验小学五(1)班大部分同学热情参与、踊跃投稿。把他们的绘画作品平均分成6组或10组,都多5幅(每人限投一幅作品)。五(1)班至少有多少人参与投稿?
37.(23-24五年级下·四川凉山·期末)2024年7月底凉山国际火把节的庆祝仪式需要用正方体的灯笼装饰街道,焊接一个灯笼框架要用去一根长240分米的铁丝(不计损耗),再给这个正方体框架的5个表面糊上彩纸,至少需要多少平方分米的彩纸?
38.(23-24五年级下·四川凉山·期末)凉山州位于四川省西南部,每年一月至五月天气干燥雨水少,属于护林防火期,在护林防火区域会准备储存水用的水箱,水箱是一个铁皮做成的无盖正方体,棱长25分米(铁皮厚度忽略)。如果每立方米水重1吨,这个水箱能装水多少吨?
39.(23-24五年级下·四川凉山·期末)2024年巴黎奥运会将于7月26日晚上7:30开幕,届时中国队将派出四百多名运动员参赛,为了保证中国运动员的营养供给,中国体协决定由某公司赞助牛奶。该公司250毫升牛奶盒长6厘米,宽4厘米,高10.5厘米。做500个这样的纸盒至少需要多少平方米的硬纸板?
40.(23-24五年级下·湖南长沙·期末)如图,一个无盖的长方体玻璃鱼缸,长50厘米、宽30厘米、高25厘米。
现将一块高14厘米,体积为1000立方厘米的假石山放入缸内。如果水龙头以每分5000毫升的流量向鱼缸内注水,那么至少需要多少分钟才能将假石山完全淹没?
41.(23-24五年级下·四川广元·期末)学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
42.(23-24五年级下·四川广元·期末)大理石是重结晶的石灰岩,因最初产地在我国云南大理而得名,主要用于加工成各种形材。当地一家加工厂将一块长60厘米、宽4分米、高32厘米的大理石截成同样大小的正方体(棱长为整厘米数),且没有剩余,截成的正方体的棱长最长是多少?一共可以截成多少个这样的正方体?
43.(23-24五年级下·四川广元·期末)荣老师:“我买一些普通跳绳和计数跳绳,付给您100元。”售货员:“我口算了一下,应该找给您14元。”荣老师:“不对,您肯定算错了。”你能解释一下,荣老师为什么这么肯定售货员算错了吗?
44.(23-24五年级下·四川广元·期末)一个长方体玻璃鱼缸(无盖),量得它的长是8分米,宽是5分米,高是6分米,水深5.4分米。(玻璃厚度忽略不计)
(1)做这个长方体玻璃鱼缸至少需要玻璃多少平方分米?
(2)如果在这个鱼缸里投入一个棱长是3分米的正方体铁块,鱼缸里的水会不会溢出?请你通过计算说明。
(3)如果会溢出,鱼缸里会溢出多少升水?如果不会溢出,现在水深是多少分米?
45.(23-24五年级下·四川凉山·期末)暑假期间玲玲一家准备到西藏自驾游,西昌到西藏拉萨全程两千多千米。玲玲家的越野车油箱从里面量长1米,宽0.4米,高0.2米,油价为7.86元/升,加满一箱油要用多少钱?
46.(23-24五年级下·湖南长沙·期末)张大爷家承包了10亩土地,其中种蔬菜,种粮食,其余种果树。种果树的面积占总面积的几分之几?
47.(23-24五年级下·湖南长沙·期末)刘老师买一种乳酸菌饮料。甲超市价格为15元7盒,乙超市价格为17元8盒,丙超市价格为9元4盒。哪家超市的这种乳酸菌饮料最便宜?
48.(23-24五年级下·湖南长沙·期末)王爷爷有一个长方形的花园,长35米,宽15米。他想把这个花园分成若干个大小相同的正方形区域(正方形边长为整米数)来种植不同的花卉。王爷爷最少可以将花园分成多少个这样的正方形区域?边长是多少米?
49.(19-20五年级上·全国·期末)将7.6立方米的沙子铺在一个长5米、宽38分米的沙坑里,可以铺多厚?
50.(23-24四年级下·河北唐山·期末)工程队修一条路,第一周修了全长的,第二周修了全长的,还剩全长的几分之几没有修?
51.(2024·四川乐山·小升初真题)一个长方体的玻璃缸,长9分米,宽8分米,高6分米,水深4.5分米,如果投入一块棱长为5分米的正方体铁块,缸里的水会溢出吗?如果溢出,会溢出多少升?
52.(2024·四川内江·小升初真题)1路公交车从站过站到站,然后返回,去时在站停车,而返回时到站不停车,去时车速为每小时48千米。
结合图中信息,完成以下问题:
(1)求站到站的路程。
(2)求返回的车速。
53.(2024·福建莆田·小升初真题)学校新修一个游泳池,长25米,宽21米,最浅处水深1.2米,最深处水深1.6米(说明:游泳池底面是倾斜的),如图所示。这个游泳池最多能蓄水多少立方米?
54.(2024·四川乐山·小升初真题)某次跳绳比赛中,选手们每分钟跳绳个数统计图如图所示,仔细观察后,回答下列问题:
(1)每分钟跳绳个数在100个以上(含100个)的选手人数是多少?
(2)每分钟跳绳个数少于100个的选手人数是每分钟跳绳个数在100个以上(含100个)的选手人数的几分之几?
55.(2024·福建宁德·小升初真题)下面是某旅游景点去年接待游客情况统计图。
(1)根据图中的数据,把统计表填写完整。
季度 合计 第一季度 第二季度 第三季度 第四季度
人数/万
(2)平均每月接待游客多少万人?
(3)如果要对这个景点进行整修,根据如图,你觉得选什么时间比较合适?请说明理由。
56.(2024·浙江杭州·小升初真题)一批货物重120吨,运走50吨。运走了几分之几?剩下的占总数的几分之几?
57.(2024·浙江杭州·小升初真题)去年,某厂计划生产一批玩具,结果上半年完成计划的,下半年完成了计划的,该厂去年超额完成了计划的几分之几?
58.(2024·浙江杭州·小升初真题)如表分别是小红和小英两位同学5次跳绳(每次1分钟)情况的统计表和统计图。
小红5次跳绳情况统计表
次数 第1次 第2次 第3次 第4次 第5次
下数(下) 120 113 130 120 135
(1)根据统计表的数据,请在如图的统计图中画出表示小红跳绳情况的折线。
(2)看图解答下面的问题:小英平均每次跳绳多少下?
59.(2024·浙江温州·小升初真题)亮亮利用两种方法测量一块石块的体积。(单位:厘米)
方法一 方法二
(1)这两种方法相同的地方是 。
(2)请选择你喜欢的一种方法计算这块石块的体积。
60.(2024·浙江杭州·小升初真题)小红家有一些鸡蛋,5个5个地数,6个6个地数都多出了2个,已知这些鸡蛋总数在80到100个之间。你能算出小红家有多少个鸡蛋吗?
61.(2024·河南郑州·小升初真题)邮递员小王从县城出发,骑自行车到A村投递,途中遇到县城中学的学生李明从A村步行返校。小王在A村完成投递工作后,返回县城途中又遇到李明,便用自行车载上李明,一起到达县城,结果小王比预计时间晚到1分钟。二人与县城间的距离(千米)和小王从县城出发后所用时间(分)之间的关系如图所示,假设二人之间交流的时间忽略不计,求:
(a)小王和李明第一次遇到时,距县城多少千米?
(b)小王从县城出发到返回县城所用时间是多少?
(c)李明从A村到县城共用多长时间?
62.(2024·重庆丰都·小升初真题)探究与运用。
(1)探究:请你举出“两个相邻奇数相乘的例子”,再观察它们所得积末尾数字的特征。(例子要包含积末尾数字不同的情况)
(2)发现:两个相邻奇数相乘,积末尾数字一定是( )和( )。
(3)运用:下面三个数中,只有一个数是两个相邻奇数的积,它是( )。
A.337 B.1661 C.3363
(4)这两个奇数分别是( )和( )。
63.(2024·浙江杭州·小升初真题)如图所示,图①和图②是两块形状不同的铁皮,将每块铁皮弯折后焊接成一个无盖的长方体铁桶(②号焊接成的是一个底面为正方形的无盖长方体),哪个铁桶的容积更大?
64.(2024·浙江杭州·小升初真题)某小学建一个长方体游泳池,长80米,宽25米,深2米。
(1)在游泳池的底部和四周贴瓷砖,贴瓷砖的面积有多少平方米?
(2)如果在游泳池内注水到1.2米的高度,那么需要注入多少立方米的水?
65.(2024·河北石家庄·小升初真题)如图是一辆公交车从起始站至终点站的行驶过程中乘客上下车情况统计图。
(1)请把统计图中的图例补充完整。
(2)从图中可以看出,第( )站上车乘客和下车乘客一样多,第( )站下车乘客最多。
(3)这辆公交车最多时载( )位乘客。
66.(2024·山东临沂·小升初真题)六(2)班的4名同学观察并测量了一个长方体,得到了5条信息:
信息1:如果高再增加3厘米,那么它恰好是一个正方体。
信息2:长方体的侧面积是280平方厘米。
信息3:长方体的表面积是480平方厘米。
信息4:长方体的棱长总和是108厘米。
信息5:长方体的底面周长是40厘米。
这5条信息都是正确的,请从中选择需要的信息,求出这个长方体的体积。
67.(2024·浙江杭州·小升初真题)一个长方体的长是10厘米,如果将长增加4厘米,则体积增加25立方厘米,那么,原来长方体的体积是多少立方厘米?
68.(2024·浙江杭州·小升初真题)暑假,王老师一家自驾去离家380千米的景点玩,如图是他们离家的距离与汽车行驶时间之间的关系图。
(1)王老师一家出发30分钟时,离家多少千米?
(2)出发后3小时,距离目的地多少千米?
69.(2024·四川绵阳·小升初真题)在下午3:00与4:00之间,求分针与时针成60度角的时间。
70.(2024·浙江湖州·小升初真题)一辆货车从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地。已知甲乙两地的路程是330千米,货车在途中停留半小时。两车离甲地的路程与时间关系如图所示。轿车比货车早几小时到达乙地?
参考答案
1.
【分析】求一个数是另一个数的几分之几用除法计算,据此解答即可。
【解析】21÷37=
答:大龙舟代表队的参赛支数是参赛代表队总支数的。
2.经过公园的路近
【分析】小美家到邮局是千米,邮局到学校是千米;小美家到公园是千米,公园到学校是千米,把这两条路线的长度相加,再比较哪个路程最短即可;计算时根据异分母分数加减法的计算方法,先通分,再按照同分母分数加减法的计算方法计算即可。
【解析】+=+=(千米)
+=+=(千米)
<
答:走经过公园的路比较近。
3.32000÷(32000÷16+32000÷20)
【分析】由题意可知,先根据工作效率=工作总量÷工作时间,分别用32000÷16和32000÷20求出甲、乙的工作效率,再根据工作时间=工作总量÷甲乙合作的工作效率,据此解答即可。
【解析】32000÷(32000÷16+32000÷20)
=32000÷(2000+1600)
=32000÷3600
=(天)
答:如果两组生产线合做,天可以完成。
4.20厘米;12个
【分析】根据题意,裁成的正方形边长最大是多少,就是求80和60的最大公因数,求至少可以裁成多少个这样的正方形,用这张纸的面积除以正方形面积,由此解答即可。
【解析】80=2×2×2×2×5,60=2×2×3×5
80和60的最大公因数是2×2×5=20
即裁成的小正方形的边长最大是20厘米。
(80×60)÷(20×20)
=4800÷400
=12(个)
答:剪出小正方形的边长最大是20厘米,至少可以剪12个这样的小正方形。
5.
【分析】把整节课的时间看作单位“1”,根据分数减法的意义,用1减去老师讲解的时间占的分率,再减去学生小组探究的时间占的分率,即可求出做练习的时间占整节课的分率。
【解析】1--
=1--
=
答:做练习的时间占整节课的。
6.(1)470平方厘米
(2)900立方厘米
【分析】(1)从设计图中可知,这个长方体水槽的长是20厘米,宽是9厘米,高是5厘米,这个水槽的表面积等于五个铁皮的面积和。
(2)长方体的体积=长×宽×高,将数据代入公式计算。
【解析】(1)20×9+20×5×2+5×9×2
=180+200+90
=470(平方厘米)
答:制作这个水槽至少需要铁皮470平方厘米。
(2)20×9×5=900(立方厘米)
答:它的容积有900立方厘米。
7.(1)35;
(2)15;30
(3)35;40
【分析】(1)虚线表示甲飞机数据,实线表示乙飞机数据,观察实线和虚线最右侧数据,即可知道飞行时间;将乙飞机飞行时间看作单位“1”,甲飞机飞行时间÷乙飞机飞行时间=甲飞机飞行时间是乙飞机飞行时间的几分之几;
(2)观察复式折线统计图,两数据点高度一样时,飞行高度一样,两数据点相距越远表示飞行高度相差越大,分别观察横轴相应时间即可;
(3)观察复式折线统计图中的虚线,折线往下坡度越陡,表示飞行高度下降越快,观察横轴对应时间即可。
【解析】(1)40÷35==
乙飞机共飞行了35秒,甲飞机飞行时间是乙飞机飞行时间的。
(2)当飞到第15秒时,两架飞机的飞行高度一样;当飞到第30秒时,两架飞机的飞行高度相差最大。
(3)从第35秒到第40秒,甲飞机的飞行高度下降得最快。
8.(1)见详解
(2)种生菜区域占这块地的几分之几
(3)
【分析】(1)已知这块地的区域种黄瓜,根据分数的意义可知,把这块地的总面积看作单位“1”,平均分成8份,种黄瓜占了其中的3份,据此在图中用斜线表示出种黄瓜的区域。
(2)把这块地的总面积看作单位“1”,算式表示用“1”减去种西红柿区域与种黄瓜区域一共占这块地的分率之和,即是种生菜区域占这块地的几分之几。
(3)先求出种生菜区域占这块地的几分之几,再减去种西红柿区域占这块地的,即是种生菜区域比种西红柿区域多占这块地的几分之几。
【解析】(1)如图:
(2)算式要解决的问题是(种生菜区域占这块地的几分之几)。
(3)
答:种生菜区域比种西红柿区域多占这块地的。
9.256立方厘米
【分析】红薯的体积等于红薯取出前后水变化的体积,水的体积相当于长8厘米、宽为8厘米,高为(14-10)厘米的长方体的体积,长方体体积=长×宽×高,据此列式计算。
【解析】8×8×(14-10)
=64×4
=256(立方厘米)
答:红薯的体积是256立方厘米。
10.
【分析】把参加马拉松比赛的总人数看作单位“1”,求参加半程马拉松的人占总人数的几分之几,用1减去参加全程马拉松的人占总人数的,再减去参加欢乐跑的人占总人数的,据此列式解答。
【解析】1--
=-
=
答:参加半程马拉松的人占总人数的。
11.(1)
(2)
(3)问题:最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的几分之几?
【分析】(1)根据统计表可知,最喜欢冰箱贴的人数占总人数的,最喜欢抱枕的人数占总人数的,用()计算;
(2)最喜欢钥匙扣的人数占总人数的,最喜欢水杯的人数占总人数的,用()计算;
(3)可以提问一个与最喜欢钥匙扣的人数相关的问题:如最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的几分之几?(答案不唯一)
【解析】(1)
答:最喜欢冰箱贴和抱枕的人数共占总人数的。
(2)
答:最喜欢钥匙扣的比水杯的人数多占总人数的。
(3)问题:最喜欢冰箱贴的比最喜欢钥匙扣的多占总人数的几分之几?
答:最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的。
12.(1)可以
(2)8800平方厘米
【分析】(1)把张阿姨行李箱的长、宽、高与免费托运行李限制的长、宽、高进行比较,如果小于或等于免费托运行李限制的尺寸,就可以免费托运;反之,不可以免费托运。
(2)根据题意,给这个行李箱加个布套(底面不做),即做布套的面是长方体的上面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是这个布套至少需要布料的面积。
【解析】(1)40<60,25<40,60<100
张阿姨的行李可以免费托运。
可以 不可以
(2)40×25+40×60×2+25×60×2
=1000+4800+3000
=8800(平方厘米)
答:这个布套至少需要8800平方厘米布料。
13.10时40分
【分析】从图中可知,65路公交车每20分钟一班,95路公交车每25分钟一班,那么这两车同时到站的时间间隔是20、25的最小公倍数,再加上第一次同时到站的时刻,就是下一次这两路公交车同时到站的时刻。
【解析】20=2×2×5
25=5×5
20和25的最小公倍数是2×2×5×5=100;
即每100分钟这两路公交车同时到站。
100分钟=1时40分
9时+1时40分=10时40分
答:下一次这两路公交车同时到“学府街关林路口”公交车站是10时40分。
14.(1)
(2)5月23日
【分析】(1)把全书的总页数看作单位“1”,聪聪第一天、第二天分别看了全书的、,根据减法的意义,用“1”减去第一天、第二天看了全书的分率,即是还剩这本书的几分之几没有看。
(2)已知睿睿每3天去一次,敏敏每5天去一次,他们在图书馆相遇的间隔天数就是3和5的最小公倍数;先求出3和5的最小公倍数,再加上他们上一次在图书馆相遇的日期,即是下次在图书馆相遇的日期。
【解析】(1)1--
=-
=-
=
答:还剩这本书的没有看。
(2)3和5的最小公倍数是:3×5=15
即每15天两人在图书馆相遇。
5月8日+15日=5月23日
答:他们下次在图书馆相遇是5月23日。
15.850平方厘米
【分析】根据题意,王老师制作这套图书的封套包裹了书的上下面、左右面和后面共5个面,根据“长×宽×2+宽×高×2+长×高”求出这5个面的面积之和,即是至少需要硬纸板的面积。
【解析】5×15×2+15×20×2+5×20
=150+600+100
=850(平方厘米)
答:至少需要850平方厘米的硬纸板。
16.(1)1700平方米
(2)56.96立方米
【分析】(1)由题可知,要在“水立方”游泳池四壁和底面贴瓷片,则贴瓷片的面积等于游泳池五个面的面积之和(除去上面),根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,进行计算即可;
(2)根据长方体的体积公式:体积=长×宽×高,据此求出一条赛道需要用的冰的体积,再乘4即可,注意单位名数的统一。
【解析】(1)50×25+(50×3+25×3)×2
=1250+(150+75)×2
=1250+225×2
=1250+450
=1700(平方米)
答:贴瓷片的面积至少是1700平方米。
(2)8厘米=0.08米
44.5×4×0.08×4
=178×0.08×4
=14.24×4
=56.96(立方米)
答:一共需要用冰大约56.96立方米。
17.
【分析】以月球土壤总量为单位“1”,用单位“1”减去氧、硅、铁的分率,即可得其它成分占月球土壤成分的分率。
【解析】1---
=---
=
答:其它成分占月球土壤成分的。
18.7800立方厘米
【分析】这个亚当牛尊工艺品的体积等于上升的这部分水的体积,根据长方体的体积=长×宽×高,用长方体容器的底面积乘水上升的高度,计算出上升这部分水的体积,也就是这个亚当牛尊工艺品的体积。
【解析】65×40×(15-12)
=2600×3
=7800(立方厘米)
答:亚当牛尊工艺品的体积是7800立方厘米。
19.15000立方厘米
【分析】根据题意可知,水面上升的部分的体积就是珊瑚的体积,根据长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】50×30×10
=1500×10
=15000(立方厘米)
答:珊瑚的体积是15000立方厘米。
20.土豆的体积是144立方厘米,红薯的体积是240立方厘米。
【分析】放入物体后,上升的水的体积就是物体的体积,根据,放入土豆后,水面上升了厘米,上升的水的体积就是土豆的体积;放入红薯水面上升了厘米,上升的水的体积就是红薯的体积。代入数据计算即可得解。
【解析】土豆的体积:
(立方厘米)
红薯的体积:
(立方厘米)
答:土豆的体积是144立方厘米,红薯的体积是240立方厘米。
21.(1)576平方厘米
(2)1296立方厘米
【分析】(1)贴彩纸的面积=长方形纸板的面积-4个正方形的面积,长方形面积=长×宽,正方形面积=边长×边长,据此列式解答;
(2)长方体的长=长方形的长-正方形边长×2,长方体的宽=长方形的宽-正方形边长×2,长方体的高=正方形的边长,根据长方体容积=长×宽×高,列式解答即可。
【解析】(1)30×24-6×6×4
=720-144
=576(平方厘米)
答:贴彩纸的面积是576平方厘米。
(2)30-6×2
=30-12
=18(厘米)
24-6×2
=24-12
=12(厘米)
18×12×6=1296(立方厘米)
答:这个盒子的容积是1296立方厘米。
22.864立方米
【分析】根据长方体体积=长×宽×高,求出一个水池的容积,再乘2即可,注意统一单位。
【解析】20厘米=0.2米
90×24×0.2×2
=432×2
=864(立方米)
答:需要注入864立方米的水。
23.5.36平方米
【分析】求展示罩的面积相当于求长方体表面积,因为无底,展示罩的面积=长×宽+长×高×2+宽×高×2,据此列式解答。
【解析】
(平方米)
答:制作一个这样透明展示罩需要5.36平方米的材料。
24.小时
【分析】求参观这三个馆一共用了多长时间,就是求小时、小时、小时的和,列分数连加法算式解答。
【解析】
(小时)
答:小明参观这三个馆一共用了小时。
25.0.63元
【分析】由于⑤和①是正方形,当一个长方体有两个面是正方形,其他四个侧面是一样的长方形,通过图可知,长是6厘米,那么宽也是6厘米,高是3厘米,通过图可知,缺少了一个长是6厘米,宽是3厘米的长方形的面;根据正方形的面积公式:边长×边长,求出一个正方形的面积再乘2,长方形的面积:长×宽,求出一个长方形的面积再乘3,把这两部分相加即可求出这个无盖纸盒的表面积,根据1平方米=10000平方厘米,转换单位,再用表面积乘每平方米的价钱,即可求出需要的总钱数。
【解析】6×6×2+6×3×3
=72+54
=126(平方厘米)
126平方厘米=0.0126平方米
0.0126×50=0.63(元)
答:做这个纸盒至少需要0.63元。
26.;
【分析】将这条路的全长看作单位“1”,第一周修的长度÷全长=第一周修了这条路的几分之几;1-第一周修了这条路的几分之几-第二周修了这条路的几分之几=还剩几分之几没有修,据此列式解答。
【解析】500÷1500==
1--
=-
=-
=
答:工程队第一周修了这条路的,两周后这条路还剩没有修。
27.8厘米
【分析】根据正方体棱长总和=棱长×12,求出铁丝长度,再根据长方体的高=棱长总和÷4-长-宽,列式解答即可。
【解析】10×12÷4-14-8
=120÷4-14-8
=30-14-8
=16-8
=8(厘米)
答:长方体框架的高是8厘米。
28.3分钟
【分析】先确定把假山完全淹没需要的水的体积,即为长、宽、高分别为6分米、4分米、1.5分米的水的体积再减去假山的体积,求出需要注水的体积,又知道每分钟注水量,再根据:时间=总量÷速度,用需要注水的体积除以10立方分米即可解答。
【解析】(6×4×1.5-6)÷10
=(24×1.5-6)÷10
=(36-6)÷10
=30÷10
=3(分钟)
答:至少需要3分钟才能把假山石刚好淹没。
29.吨
【分析】由题意可知,储存小米的质量=储存大米的质量-吨,储存面粉的质量=储存小米的质量+0.4吨,据此解答。
【解析】-+0.4
=-+
=+-
=1-
=(吨)
答:这个仓库储存了吨面粉。
30.160平方分米
【分析】由图可知,相交于同一顶点的3条棱的长度分别是4分米、4分米、8分米,根据“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个长方体的表面积,据此解答。
【解析】(4×4+4×8+4×8)×2
=(16+32+32)×2
=80×2
=160(平方分米)
答:这个长方体的表面积是160平方分米。
31.24升
【分析】求缸里的水会溢出多少,就是求正方体铁块的体积比长方体玻璃水缸还能容纳物体的体积多多少,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,分别求出正方体铁块的体积和长方体玻璃水缸还能容纳物体的体积,再用正方体铁块的体积减去长方体玻璃水缸还能容纳物体的体积,求出缸里的水溢出多少立方分米,再根据1立方分米=1升,把立方分米化为升即可解答。
【解析】4×4×4-8×5×(5-4)
=16×4-40×1
=64-40
=24(立方分米)
24立方分米=24升
答:缸里的水会溢出24升。
32.(1)23;30;
(2)上升;
(3)小林同学;见详解
【分析】(1)复式折线统计图中,横轴表示时间,纵轴表示数量,实线表示小林一周每天一分钟跳绳的情况,虚线表示小丽一周每天一分钟跳绳的情况,折点位置越高跳绳数量越多,折点位置越低跳绳数量越少;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线走势向上总体呈现上升趋势,折线走势向下总体呈现下降趋势;
(3)从两条折线的走势分析两位同学的跳绳情况,选择成绩波动较小且呈上升趋势的同学即可。
【解析】(1)小林:218-195=23(个)
小丽:223-193=30(个)
所以,小林同学一分钟跳绳的最高成绩与最低成绩相差23个,小丽同学一分钟跳绳的最高成绩与最低成绩相差30个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现上升趋势。
(3)推荐小林同学,观察复式折线统计图可知,小丽的成绩波动较大,小林的成绩稳定且整体呈现上升趋势。(答案不唯一)
33.
【分析】先求出这第二天一共卖的箱数,再除以矿泉水的总箱数,即是这两天一共卖了所有矿泉水的几分之几。
【解析】12+20=32(箱)
32÷96=
答:两天一共卖了所有矿泉水的。
34.
【分析】将总时间看作单位“1”,1-往返路上用去的时间占总时间的几分之几-休息的时间占总时间的几分之几=参观学习时间占总时间的几分之几。
【解析】1--
=-
=-
=
=
答:参观学习时间占总时间的。
35.(1)二
(2)六;10
(3)B款;理由见详解
【分析】(1)观察复式折线统计图,当两条折线相交于一点时,说明这一天两款扫地机器人的清扫时长相同。
(2)观察复式折线统计图,当两条折线的叉口最大时,说明两款扫地机器人的清扫时长相差最大,再用减法求出相差的时间。
(3)在两款扫地机器人清扫效果大致相同的情况下,选择清扫时长较短的扫地机器人更合适,说明理由,合理即可。
【解析】(1)试验第二天,两款扫地机器人的清扫时长相同。
(2)16-6=10(分钟)
试验第六天,两款扫地机器人的清扫时长相差最大,相差10分钟。
(3)如果两款扫地机器人清扫效果大致相同,该公司会批量生产B款扫地机器人,因为随着清扫天数的增加,B款清扫用时逐渐减少且趋于平稳,说明它更智能、更省电。
36.35人
【分析】他们的绘画作品平均分成6组或10组,都多5幅,由此可知,他们的作品的总数量减去5就是6和10的公倍数,由于每人限投一幅作品,则五(1)班至少人数是6和10的最小公倍数,再加上5,根据求两个数最小公倍数的方法:两个数的公有质因数与每一个独有质因数连乘积,就是最小公倍数,如果两个数为倍数关系,则最小公倍数为较大的数,如果两个数为互质数,则最小公倍数为两个数的乘积,据此解答。
【解析】6=2×3
10=2×5
6和10的最小公倍数是2×3×5=30
30+5=35(人)
答:五(1)班至少有35人参与投稿。
37.2000平方分米
【分析】由题意可知,240分米是正方体的棱长总和,根据的逆运算,用240除以12可得棱长,再根据正方体表面积的特征,用棱长乘棱长乘5,即可得解。
【解析】(分米)
(平方分米)
答:至少需要2000平方分米的彩纸。
38.15.625吨
【分析】根据题意,水箱是一个铁皮做成的棱长25分米的无盖正方体,根据正方体的体积(容积)公式V=a3,求出水箱的容积,再根据进率“1立方米=1000立方分米”换算单位;然后用每立方米水的重量乘水箱的容积,即可求出这个水箱能装水的总重量。
【解析】25×25×25
=625×25
=15625(立方分米)
15625立方分米=15.625立方米
1×15.625=15.625(吨)
答:这个水箱能装水15.625吨。
39.12.9平方米
【分析】已知牛奶盒长6厘米、宽4厘米、高10.5厘米,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出1个牛奶盒的表面积,再乘500,即是做500个这样的纸盒至少需要硬纸板的面积。注意单位的换算:1平方米=10000平方厘米。
【解析】(6×4+6×10.5+4×10.5)×2
=(24+63+42)×2
=129×2
=258(平方厘米)
258×500=129000(平方厘米)
129000平方厘米=12.9平方米
答:做500个这样的纸盒至少需要12.9平方米的硬纸板。
40.4分钟
【分析】根据题意,要将一块高14厘米,体积为1000立方厘米的假石山完全淹没,那么要向长方体鱼缸内注入14厘米高的水;根据长方体的体积=长×宽×高,求出将假石山完全浸没水和假山石的体积之和,再减去假山石的体积,即是需注入水的体积;然后根据进率“1立方厘米=1毫升”换算单位;
已知水龙头以每分5000毫升的流量向鱼缸内注水,用注入水的体积除以水的流速,即可求出时间。
【解析】50×30×14
=1500×14
=21000(立方厘米)
21000-1000=20000(立方厘米)
20000立方厘米=20000毫升
20000÷5000=4(分钟)
答:至少需要4分钟才能将假石山完全淹没。
41.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【解析】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
42.4厘米;1200个
【分析】4分米=40厘米,由题意可知,求截成的正方体的棱长最长是多少,就是求60、40、32的最大公因数,先把60、40、32分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数;用60、40、32分别除以它们的最大公因数,再把它们的商相乘即可解答。
【解析】4分米=40厘米
60=2×2×3×5
40=2×2×2×5
32=2×2×2×2×2
60、40、32的最大公因数是2×2=4
所以正方体棱长最长是4厘米;
(60÷4)×(40÷4)×(32÷4)
=15×10×8
=150×8
=1200(块)
答:截成的正方体的棱长最长是4厘米,一共可以截成1200个这样的正方体。
43.见详解
【分析】根据5的倍数特征:个位上是0或5的数,都是5的倍数;因为跳绳的单价是5元,计数跳绳的单价是10元;10是5的倍数,所以无论买多少根跳绳和计数跳绳,那么花的钱数和找回的钱数一定是5的倍数,据此解答。
【解析】100-14=86(元)
根据两种跳绳单价可知,荣老师花的钱数应是5的倍数,找回的钱数也是5的倍数,但是花的钱数86不是5的倍数,找回的钱数14也不是5的倍数,所以荣老师这么肯定售货员算错了。
44.(1)196平方分米
(2)会溢出;见详解
(3)3升
【分析】(1)从图中可知:这个长方体的长是8分米,宽是5分米,高是6分米。这个无盖的长方体有下面和前后左右面共5个面,因此需要玻璃的面积= 长×宽+长×高×2+宽×高×2,代入数据计算即可。
(2)此时水深5.4分米,还剩下空间的高度6-5.4=0.6分米,根据长方体的体积(容积)=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算,分别求出剩下空间的容积、正方体的体积,再比较即可。
(3)若溢出,用正方体的体积减去剩下空间的容积,即可求出溢出的水量(换算成以升为单位);若不会溢出,用正方体的体积÷长方体的底面积,求出正方体放入水中后,水面升高的高度,再加上原来的水面高度,即可求出现在的水面高度。
【解析】(1)8×5+8×6×2+5×6×2
=40+96+60
=196(平方分米)
答:做这个长方体玻璃鱼缸至少需要玻璃196平方分米。
(2)3×3×3=27(立方分米)
8×5×(6-5.4)
=8×5×0.6
=24(立方分米)
27>24
答:鱼缸里的水会溢出。
(3)27-24=3(立方分米)
3立方分米=3升
答:鱼缸里会溢出3升水。
45.628.8元
【分析】根据长方体的体积=长×宽×高,代入数据求出油箱的容积,进而根据1立方米=1000升换算成升,再根据单价×数量=总价,用油箱的升数乘7.86即可求出加满这箱油要多少钱。
【解析】1×0.4×0.2=0.08(立方米)
0.08立方米=80升
80×7.86=628.8(元)
答:加满一箱油要用628.8元。
46.
【分析】把承包的10亩土地看作整体“1”,用“1”减去种蔬菜和种粮食的面积占总面积的分率和,即可得解。
【解析】1-(+)
=1-(+)
=1-
=
答:种果树的面积占总面积的。
47.乙超市
【分析】根据总价÷数量=单价,分别计算出三家超市1盒乳酸菌饮料的钱数,比较即可。根据分数与除法的关系表示出结果,即分数的分子相当于被除数,分母相当于除数,再将假分数化成带分数,即可比较出大小。假分数化带分数:用分子除以分母,当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【解析】15÷7==(元)
17÷8==(元)
9÷4==(元)
<<
答:乙超市的这种乳酸菌饮料最便宜。
48.21个;5米
【分析】要想将花园分成的正方形区域越少,分成的正方形就要尽可能的大。求出长方形长和宽的最大公因数,是分成的最大正方形的边长,长方形面积=长×宽,正方形面积=边长×边长,长方形面积÷正方形面积=分成的正方形个数,据此列式解答。
【解析】35=5×7
15=3×5
35和15的最大公因数是5,因此正方形边长是5米。
35×15÷(5×5)
=525÷25
=21(个)
答:王爷爷最少可以将花园分成21个这样的正方形区域,边长是5米。
49.0.4米
【分析】先统一单位,然后根据长方体的高=体积÷长÷宽,代入数据即可解答。
【解析】38分米=3.8米
7.6÷5÷3.8
=1.52÷3.8
=0.4(米)
答:可以铺0.4米厚。
50.
【分析】将这条路的全长看作单位“1”,用单位“1”依次减去第一周和第二周修的占全长的分率,即可求出剩下没修的占全长的几分之几。
【解析】1--
=-
=
=
答:还剩全长的没有修。
51.会溢出;17升
【分析】根据长方体体积公式:体积=长×宽×高;先求出高是(6-4.5)分米空白体积,再根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体铁块的体积,再用高是(6-4.5)分米空白部分体积与正方体铁块的体积比较,如果高是(6-4.5)分米空白部分的体积大于正方体铁块的体积,水不会溢出;如果高是(6-4.5)分米空白部分的体积小于正方体铁块的体积,水会溢出,再用正方体铁块的体积-高是(6-4.5)分米空白部分的体积,即可求出溢出的水的体积,注意单位名数的换算。据此解答。
【解析】9×8×(6-4.5)
=72×1.5
=108(立方分米)
5×5×5
=25×5
=125(立方分米)
125>108
125-108=17(立方分米)
17立方分米=17升
答:缸里的水会溢出,溢出17升。
52.(1)3.2千米;(2)72千米
【分析】(1)由图上发现,从到用了4分钟,根据路程速度时间可,以求出站到站的路程。
(2)发现回来一共用了6分钟,去的时候从到一共用了5分钟,可以求出到的路程,再加上站到站的路程即可求出总路程,用路程时间速度,可以求出返回的速度。
【解析】(1)48千米时千米分
(千米)
答:站到站的路程是3.2千米。
(2)(分钟)
(千米)
(分钟)
(千米)
1.2×60=72(千米)
答:返回的车速是每小时72千米。
53.735立方米
【分析】观察题意可知,以梯形的一面为底面,首先根据梯形的面积公式:S=(a+b)h÷2,求出底面积,然后根据体积=底面积×高,即可求出这个游泳池最多能蓄水的多少立方米。
【解析】(1.2+1.6)×25÷2×21
=2.8×25÷2×21
=35×21
=735(立方米)
答:这个游泳池最多能蓄水735立方米。
54.(1)22人
(2)
【分析】(1)从条形统计图中可知,每分钟跳绳个数在100~109个的选手有15人,每分钟跳绳个数在110~120个的选手有7人,用加法计算,即可求出每分钟跳绳个数在100个以上(含100个)的选手人数。
(2)先用加法求出每分钟跳绳个数少于100个的选手人数,再除以每分钟跳绳个数在100个以上(含100个)的选手人数即可,结果用最简分数表示。
【解析】(1)15+7=22(人)
答:每分钟跳绳个数在100个以上(含100个)的选手人数是22人。
(2)(5+6+9)÷22
=20÷22
=
答:每分钟跳绳个数少于100个的选手人数是每分钟跳绳个数在100个以上(含100个)的选手人数的。
55.(1)18;2.5;5;6;4.5
(2)1.5万人
(3)第一季度,理由见解析
【分析】(1)观察折线统计图可知,横轴表示季度,纵轴表示人数,据此读取各季度数据填空,再把四个季度的人数相加即可得合计人数。
(2)一年有12个月,根据求平均数用除法计算,用合计人数除以12即可得解。
(3)应选择景点人数最少的季度进行整修,才不耽误旺季的营业。
【解析】(1)2.5+5+6+4.5=18(万人)
如表所示
季度 合计 第一季度 第二季度 第三季度 第四季度
人数/万 18 2.5 5 6 4.5
(2)18÷12=1.5(万人)
答:平均每月接待游客1.5万人。
(3)
答:应该在旅游人数最少的第一季度整修,这样不耽误旺季的营业。
56.;
【分析】用运走的质量除以货物的总质量,求出运走了几分之几;再把货物的总质量看作单位“1”,利用单位“1”减去运走的几分之几就是剩下的几分之几,据此解答。
【解析】
1-=
答:运走了,剩下的占总数的。
57.
【分析】把全年计划看作单位“1”,首先用某长上半年完成计划的分率加上下半年完成计划的分率,求出某长全年一共完成了计划的几分之几;然后用它减去1,求出该厂去年超额完成了计划的几分之几即可。
【解析】+-1
=-1
=
答:该厂去年超额完成了计划的。
58.(1)见详解
(2)121下
【分析】(1)根据统计表中小红跳绳的情况多少,先在图中描出各点,然后用线段顺次把各点连接起来即可。
(2)用小英5次跳的下数之和除以5即可解答。
【解析】(1)如下图所示:
(2)(115+113+120+127+130)÷5
=605÷5
=121(下)
答:小英平均每次跳绳121下。
59.(1)都是应用排水法测量实物的体积
(2)1570立方厘米
【分析】(1)方法一和方法二都是利用水的体积变化来测量石块的体积。方法一是通过测量放入石块前后水的高度变化,计算出石块的体积;方法二是通过测量溢出的水的体积来直接得到石块的体积。这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法。把石块放入有水的长方体容器中,石块完全浸没在水里(水未溢出),上升部分水的体积就等于石块的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
第②种实验方法。把石块放在盛满水的容器里,石块完全浸没在水里,水溢出来,把溢出来的水倒入圆柱体容器里,溢出的水的体积就等于石块的体积,根据圆柱体的体积公式:V=Sh(S=πr2),把数据代入公式解答。
【解析】(1)这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法:
20×15.7×(15-10)
=314×5
=1570(立方厘米)
第②种实验方法:
3.14×52×20
=3.14×25×20
=78.5×20
=1570(立方厘米)
这块石块的体积是1570立方厘米。
(选择其一即可)
60.92个
【分析】根据题意,一些鸡蛋,5个5个地数,6个6个地数都多出了2个,说明这些鸡蛋的总个数比5和6的公倍数还多2;
先求出5和6的最小公倍数,再找出在80到100之间的公倍数,最后再加上2个,即是这些鸡蛋的总个数。
【解析】5和6的最小公倍数是:5×6=30
30在80到100之间的公倍数是:30×3=90
90+2=92(个)
答:小红家有92个鸡蛋。
61.(a)4千米
(b)85分钟
(c)105分钟
【分析】从图中可以看出小王和李明并不是同时出发的,小王还有在A村停留时间30分钟,小王去A村和返回速度不一样,这些都可以从图中看出来。
(a)从图中可以看出小王30分时走了6千米,相遇时走了20分,根据、代入数据先求速度,再求路程即可。
(b)小王从县城出发到返回县城所用时间,从图中可以看出包括去时用的时间加在A村待的时间加上返回遇李明的时间加上原计划时间再加上晚到1分钟。
(c)李明从A村到县城共用时间包括自己走路用的时间和小王带他的时间。
【解析】(a)
(千米)
答:小王和李明第一次遇到时,距县城4千米。
(b)小王30分钟到A村休息30分钟返回在离县城1千米和李明相遇,用时20分钟。
返回时小王速度(6-1)÷20
=5÷20
=0.25(千米)
照原速度小王1÷0.25=4(分钟)
那么小王用时=30+30+20+4+1=85(分钟)
(c)李明从图中可以看出从离城5千米到1千米用时80分钟
李明的速度(5-1)÷80
=4÷80
=0.05(千米)
李明从A村和小王第二次相遇用时:5÷0.05=100(分钟)
李明从A村总用时=100+5=105(分钟)
答:从图中可以看出相遇时离县城4千米,小王从县城出发到返回县城所用时间是85分钟,李明从A村到县城共用105分钟。
62.(1)见详解
(2) 3、5 9
(3)C
(4) 59 57
【分析】不是2的倍数的数叫作奇数;通过举例观察两个相邻奇数相乘所得积末尾数字的特征,利用该特征解决后续问题。
【解析】(1)例子:3×5=15,积末尾数字是5;5×7=35,积末尾数字是5;7×9=63,积末尾数字是3;9×11=99,积末尾数字是9;11×13=143,积末尾数字是3。
(2)从上面所举例子可以发现:两个相邻奇数相乘,积末尾数字一定是3和5和9。
(3)A.337末尾数字是7,不符合积末尾数字是3、5、9的特征,所以337不是两个相邻奇数的积。
B.1661末尾数字是1,不符合积的末尾数字是3、5、9的特征,所以1661不是两个相邻奇数的积。
C.3363末尾数字是3,符合积的末尾数字的特征,所以它是两个相邻奇数的积。
(4)因为两个相邻奇数相差2,设较小奇数为x,则较大奇数为x+2,那么x(x+2)=3363
对3363分解质因数,3363=3×19×59=57×59,所以这两个奇数分别是57和
59。.
63.②号
【分析】根据题意,结合图形,先分别求出图①和图②每个长方体的长、宽、高,再根据:长方体的体积(容积)=长×宽×高,分别求出两个长方体铁桶的容积,然后进行比较,即可得出结论。
【解析】图①:110-60=50(厘米)
120-50-50=20(厘米)
60×20×50
=1200×50
=60000(立方厘米)
图②:120÷4=30(厘米)
100-30=70(厘米)
30×30×70
=900×70
=63000(立方厘米)
因为63000立方厘米>60000立方厘米
所以②号铁桶的容积更大。
答:②号铁桶的容积更大。
64.(1)2420平方米;(2)2400立方米
【分析】(1)游泳池是无盖的,所以贴瓷砖的面积是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式求出这5个面的总面积即可。
(2)根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【解析】(1)80×25+80×2×2+25×2×2
=2000+320+100
=2420(平方米)
答:贴瓷砖的面积有2420平方米。
(2)80×25×1.2=2400(立方米)
答:需要注入2400立方米的水。
65.见解答
【分析】(1)观察图例可见,一条实线随站次变化,表示每站“上车”人数;另一条虚线则表示“下车”人数,故应将图例补充为“上车人数”“下车人数”。
(2)从图中读数比较,可发现只有在第六站时,上车人数与下车人数相同;而虚线在第八站达到最高值,说明第八站下车人数最多。
(3)要求“最多时车上有多少乘客”,只需逐站累加(上车人数减下车人数)即可。
【解析】(1)如图:
;
(2)第六站实线与虚线相交,表示上、下车乘客一样多;第八站下车乘客最多;
(3)起始站有2位
第一站:2+9-1=10(位)
第二站:10+11-7=14(位)
第三站:14+12-8=18(位)
第四站:18+10-8=20(位)
第五站:20+13-10=23(位)
第六站:23+14-14=23(位)
第七站:23+13-15=21(位)
第八站:21+12-16=17(位)
第九站:17-13+5=9(位)
23=23>21>20>18>17>14>10>9;最多时载23位乘客。
这辆公交车最多时载23位乘客。
66.见详解
【分析】根据信息1和信息5可知,这个长方体的底面是正方形;根据正方形周长公式:周长=边长×4,边长=周长÷4,据此求出长方体的长和宽,再用边长-3厘米,求出长方体的高,再根据长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】选择信息1和信息5。
40÷4=10(厘米)
10-3=7(厘米)
10×10×7
=100×7
=700(立方厘米)
答:这个长方体的体积是700立方厘米。
67.62.5立方厘米
【分析】根据长方体的体积=长×宽×高,宽和高不变,长增加4厘米,则增加后长方体的体积=(长+4)×宽×高,原来长方体的体积=长×宽×高。已知将长增加4厘米,体积增加25立方厘米,由增加后的体积-原来的体积=25,代入数值计算出长方体的宽和高的乘积,最后用宽和高的乘积乘原来的长,所得结果即为原来长方体的体积。
【解析】(长+4)×宽×高-长×宽×高=25
化简得:宽×高×4=25
因此宽×高=25÷4=6.25
原来长方体体积:6.25×10=62.5(立方厘米)
答:原来长方体的体积是62.5立方厘米。
68.(1)40千米
(2)130千米
【分析】折线统计图的横轴代表的是时间,纵轴代表的路程,根据折线统计图可以知道王老师2.5小时行驶了200千米,4小时行驶了350千米。
(1)求王老师一家前2.5小时的速度列式:200÷2.5;求后面(4-2.5)小时的速度列式:(350-200)÷(4-2.5);
要想求出“他们出发30分钟时,离家多少千米?”就要知道此时行驶的速度,再根据路程=速度×时间即可解答,注意要把30分钟转换成小时;
(2)先求出后面(4-2.5)小时的速度,求出后面(4-2.5)小时行驶的路程。王老师2.5小时行驶了200千米,用后面(4-2.5)小时行驶的路程加上200千米,计算出前3个小时的行驶路程,总路程减去已行驶的路程即为距离目的地多少千米。
【解析】(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米。
(2)(350-200)÷(4-2.5)×(3-2.5)
=150÷1.5×0.5
=50(千米)
380-(200+50)
=380-250
=130(千米)
答:离目的地还有130千米。
69.3时分和3时分
【分析】时针每分钟走(度),分针每分钟走(度),因此分针每分钟比时针多走(度),3点时,时针在分针前方90度,因此两针夹角为60度时,分针要比时针多走(度),或者多走(度)。分别用30除以5.5,150除以5.5,即可得解。
【解析】(30×3-60)÷(6-0.5)
=(90-60)÷5.5
=30÷5.5
=(分)
(30×3+60)÷(6-0.5)
=150÷5.5
=(分)
答:在钟表上,3点倒4点之间,3时分和3时分时分针与时针成60度的角。
【点睛】本题主要考查分数和除法的关系以及追及问题,关键是求出时针和分针每分钟走的度数。
70.1.2小时
【分析】通过观察统计图可知,货车在(3-0.5)小时内行驶了150千米,根据速度=路程÷时间,可以先求出货车的速度,同时可以计算出货车行驶90千米所用的时间即a的值是1.5小时。
那么轿车在(3-1.5)小时内行驶150千米,根据速度=路程÷时间,可以求出轿车的速度。
最后再根据时间=路程÷速度,分别求出货车、轿车到达乙地各用多少小时,并根据求一个数比另一个少多少,用减法解答。
【解析】货车速度:150÷(3-0.5)
=150÷2.5
=60(千米/时)
a:90÷60=1.5(小时)
轿车速度:150÷(3-1.5)
=150÷1.5
=100(千米/时)
330÷60=5.5(小时)
330÷100=3.3(小时)
5.5+0.5-3.3-1.5
=6-3.3-1.5
=1.2(小时)
答:轿车比货车早1.2小时到达乙地。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
(人教版)五年级数学下册期末真题汇编——解答题 (70题)
1.(23-24五年级下·江西九江·期末)5月25日至26日,“庐山杯”长江经济带龙舟邀请赛在九江市南门湖举行。一共有37支代表队参赛,其中大龙舟有21支代表队,小龙舟有16支代表队。大龙舟代表队的参赛支数是参赛代表队总支数的几分之几?
2.(23-24五年级下·重庆忠县·期末)如下图,小美从家到学校有两条路,一条经过公园,另一条经过邮局。走哪条比较近?
3.(2024·湖北荆州·小升初真题)只列式,不计算。
某工厂要加工32000个零件。甲生产线单独做16天完成;乙生产线单独做20天完成。如果两组生产线合做,几天可以完成?
4.(2024·浙江杭州·小升初真题)有一张长方形纸板,长80厘米,宽60厘米,如果要剪成若干同样大小的正方形而没有剩余,剪出小正方形的边长最大是多少厘米?可以剪多少个这样的小正方形?
5.(23-24五年级下·河北唐山·期末)一节数学课时长小时。老师讲解的时间占,学生小组探究的时间占,剩下的是学生独立做练习的时间。做练习的时间占整节课的几分之几?
6.(23-24五年级下·江西赣州·期末)按下面的设计图,用铁皮焊接一个无盖的水槽。(厚度不计,单位:厘米)
(1)制作这个水槽至少需要铁皮多少平方厘米?
(2)制作好的水槽,它的容积有多大?
7.(23-24五年级下·河南洛阳·期末)下面是某航模社团制作的两架模型飞机在一次试飞中飞行时间和飞行高度的飞行记录统计图。
(1)由图可知,乙飞机共飞行了( )秒,甲飞机飞行时间是乙飞机飞行时间的。
(2)当飞到第( )秒时,两架飞机的飞行高度一样;当飞到第( )秒时,两架飞机的飞行高度相差最大。
(3)从第( )秒到第( )秒,甲飞机的飞行高度下降得最快。
8.(23-24五年级下·河南洛阳·期末)“爱学习,爱劳动,长大要为人民立功劳”,阳光小学开辟一块空地开展蔬菜种植活动,其中这块地的区域种西红柿,这块地的区域种黄瓜,其余区域种生菜。
(1)请在图中用斜线表示出种黄瓜的区域。
(2)算式要解决的问题是( )。
(3)种生菜区域比种西红柿区域多占这块地的几分之几?
9.(23-24五年级下·河南洛阳·期末)笑笑、乐乐、洛洛和阳阳四人学习了有趣的测量后,张老师让他们尝试测量一个不规则物体的体积,他们进行的实验步骤如下:
①笑笑准备了一个长和宽都是8厘米,高是15厘米的长方体玻璃缸;
②乐乐往缸里倒入一些水,此时水面距离玻璃缸口5厘米;
③洛洛把一个红薯完全浸没入水中,此时水面高度是14立方厘米;
④阳阳把红薯取出,这时水面高度是10厘米。
你能根据以上信息,计算这个红薯的体积是多少吗?
10.(23-24五年级下·河南安阳·期末)4月21日安阳市举办了甲骨文马拉松比赛。比赛分为全程马拉松、半程马拉松和欢乐跑三个项目,其中参加全程马拉松的人占总人数的,参加欢乐跑的人占总人数的,其他的是参加半程马拉松的人,参加半程马拉松的人占总人数的几分之几?
11.(23-24五年级下·河南安阳·期末)这是文创商店调查的200名顾客最喜欢的商品项目统计表。
最喜欢的文创商品 冰箱贴 抱枕 钥匙扣 水杯 其他
占总人数的几分之几
(1)最喜欢冰箱贴和抱枕的人数共占总人数的几分之几?
(2)最喜欢钥匙扣的比水杯的人数多占总人数的几分之几?
(3)请你提出一个数学问题并解答。
12.(23-24五年级下·河南洛阳·期末)乘坐飞机时免费托运行李的尺寸限制为长60厘米、宽40厘米、高100厘米。张阿姨的行李箱如下图所示。
(1)张阿姨的行李是否可以免费托运?(可以 不可以)(在方框内打“√”)
(2)张阿姨打算给这个行李箱加个布套(底面不做),这个布套至少需要多少布料?(接缝处忽略不计)
13.(23-24五年级下·河南洛阳·期末)周六上午9:00,阳阳和爸爸在“学府街关林路口”公交车站等车,正好看到65路公交车和95路公交车同时到达车站。根据这两路公交车的发车信息(如图),你知道下一次这两路公交车同时到“学府街关林路口”公交车站是几时几分吗?
65路:每20分钟一班车95路:每25分钟一班车
14.(23-24五年级下·江西九江·期末)2024年4月23日是第29个世界读书日,希望小学开展“读书节”的活动,图书馆每天都对外开放,欢迎每位学生都来图书馆阅读、借书。
(1)聪聪选了一本《趣味科学》,共280页,第一天看了全书的,第二天看了全书的,还剩这本书的几分之几没有看?
(2)睿睿和敏敏两人都在图书馆借书,睿睿每3天去一次,敏敏每5天去一次。如果5月8日他们两人在图书馆相遇,那么他们下次在图书馆相遇是几月几日?
15.(23-24五年级下·江西九江·期末)为了保护书籍,王老师打算用硬纸板为某套图书做一个封套(如下图),至少需要多少平方厘米的硬纸板?(硬纸板的厚度及接缝处忽略不计。)
16.(23-24五年级下·重庆九龙坡·期末)国家游泳中心又名“水立方”,在2022年北京冬奥会变身为“冰立方”,成为国际首个泳池上架设冰壶赛道的“双奥场馆”。
(1)在“水立方”游泳池的四壁和底面贴瓷片,贴瓷片的面积至少是多少平方米?
(2)“冰立方”内有4条冰壶赛道,一共需要用冰大约多少立方米?
17.(23-24五年级下·重庆忠县·期末)“嫦娥五号”在闯过地月转移、近月制动、环月飞行、月面着陆、自动采样、月面起飞、月轨交会对接、再入返回等多个难关后,成功携带月球样品返回地球。月球土壤成分中,氧占,硅占,铁占。除氧、硅、铁外,其它成分占月球土壤成分的几分之几?
18.(23-24五年级下·河南安阳·期末)明明买了一个亚当牛尊的工艺品,想知道它的体积是多少。明明把它放入一个长65厘米,宽40厘米,水深12厘米的容器中,结果水面升高到15厘米(水没有溢出)。你知道亚当牛尊工艺品的体积是多少立方厘米吗?
19.(23-24五年级下·江西九江·期末)小军的爸爸买了一个珊瑚,他把珊瑚放进鱼缸后,鱼缸内的水上升了10厘米,珊瑚的体积是多少立方厘米?
20.(23-24五年级下·江西吉安·期末)下面是贝贝比较土豆和红薯的体积时做的实验。(单位:厘米)
分别计算土豆和红薯的体积。
21.(23-24五年级下·河北唐山·期末)如图,花花用一张长30厘米、宽24厘米的长方形纸板,从四角各切掉一个边长6厘米的正方形,然后做成无盖盒子。
(1)如果在盒子外面贴上彩纸,贴彩纸的面积是多少平方厘米?
(2)这个盒子的容积是多少立方厘米?
22.(23-24五年级下·河南安阳·期末)殷墟博物馆新馆主体南侧有两个长90米、宽24米,深20厘米的水池。要往这两个水池中注满水,需要注入多少立方米的水?
23.(23-24五年级下·河南安阳·期末)博物馆里有许多保护文物的透明展示罩(无底),下图所示:这是其中一个,长是2米,宽0.6米,高0.8米,制作一个这样透明展示罩需要多少平方米的材料?
24.(23-24五年级下·河南安阳·期末)殷墟博物馆设有基本陈列馆、专题展览馆和特色沉浸式数字展。小明参观基本陈列馆用小时,参观专题展览馆用了小时,参观特色沉浸式数字展用小时,小明参观这三个馆一共用了多长时间?
25.(23-24五年级下·重庆忠县·期末)如下图是一个无盖长方体纸盒展开图,其中①,⑤为正方形。每平方米纸50元,做这个纸盒至少需要多少元?
26.(23-24五年级下·四川绵阳·期末)工程队修一条1500米长的路,第一周修了500米,第二周修了这条路的。工程队第一周修了这条路的几分之几?两周后这条路还剩几分之几没有修?
27.(23-24五年级下·四川绵阳·期末)用一根铁丝刚好焊成一个棱长10厘米的正方体框架,如果把它改成一个长14厘米,宽8厘米的长方体框架。长方体框架的高是多少厘米?
28.(23-24五年级下·四川绵阳·期末)在下图的玻璃鱼缸中放入一块高1.5分米、体积为6立方分米的假山石。如果水管以每分钟10立方分米的流量向鱼缸内注水,至少需要多长时间才能把假山石刚好淹没?
29.(23-24五年级下·四川南充·期末)某食堂仓库储存了吨大米,比储存的小米多吨;储存的面粉比储存的小米多0.4吨。这个仓库储存了多少吨面粉?
30.(23-24五年级下·四川南充·期末)有一个底面为正方形的长方体纸箱,下图是它的六个面中的两个面,请你根据相关数据,计算出这个长方体的表面积(连接处材料不计)。
31.(23-24五年级下·四川南充·期末)一个长方体玻璃水缸,长8分米,宽5分米,高5分米,水深4分米。如果竖直放入一块棱长为4分米的正方体铁块,缸里的水会溢出多少升?
32.(23-24五年级下·四川南充·期末)五(2)班要在小林和小丽两位同学中,选出一名同学代表班级参加学校举行的跳绳比赛。下面是他们一周每天一分钟跳绳的情况记录,请根据图中信息解决下列问题。
(1)从图中可以看出,小林同学一分钟跳绳的最高成绩与最低成绩相差( )个;小丽同学一分钟跳绳的最高成绩与最低成绩相差( )个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现( )趋势。(填“上升”或“下降”)
(3)你会推荐哪位同学代表班级参加一分钟跳绳比赛?说说你的理由。
33.(23-24五年级下·四川南充·期末)某超市有96箱矿泉水,第一天卖了12箱,第二天卖了20箱。两天一共卖了所有矿泉水的几分之几?
34.(23-24五年级下·四川南充·期末)五(1)班到罗瑞卿纪念馆开展研学活动。全程用时3小时,其中往返路上用去的时间占总时间的,休息的时间占总时间的,剩下的是参观学习时间。参观学习时间占总时间的几分之几?
35.(23-24五年级下·四川南充·期末)某科技公司研发出了A、B两款智能扫地机器人,并对其进行了六天的试验(实验条件完全相同),下面是根据它们试验期间的清扫时长制成的折线统计图。
(1)试验第( )天,两款扫地机器人的清扫时长相同。
(2)试验第( )天,两款扫地机器人的清扫时长相差最大,相差( )分钟。
(3)如果两款扫地机器人清扫效果大致相同,该公司会批量生产哪一款?请说明。
36.(23-24五年级下·四川南充·期末)在“美丽中国行,我是行动者”生态环保主题绘画比赛中,实验小学五(1)班大部分同学热情参与、踊跃投稿。把他们的绘画作品平均分成6组或10组,都多5幅(每人限投一幅作品)。五(1)班至少有多少人参与投稿?
37.(23-24五年级下·四川凉山·期末)2024年7月底凉山国际火把节的庆祝仪式需要用正方体的灯笼装饰街道,焊接一个灯笼框架要用去一根长240分米的铁丝(不计损耗),再给这个正方体框架的5个表面糊上彩纸,至少需要多少平方分米的彩纸?
38.(23-24五年级下·四川凉山·期末)凉山州位于四川省西南部,每年一月至五月天气干燥雨水少,属于护林防火期,在护林防火区域会准备储存水用的水箱,水箱是一个铁皮做成的无盖正方体,棱长25分米(铁皮厚度忽略)。如果每立方米水重1吨,这个水箱能装水多少吨?
39.(23-24五年级下·四川凉山·期末)2024年巴黎奥运会将于7月26日晚上7:30开幕,届时中国队将派出四百多名运动员参赛,为了保证中国运动员的营养供给,中国体协决定由某公司赞助牛奶。该公司250毫升牛奶盒长6厘米,宽4厘米,高10.5厘米。做500个这样的纸盒至少需要多少平方米的硬纸板?
40.(23-24五年级下·湖南长沙·期末)如图,一个无盖的长方体玻璃鱼缸,长50厘米、宽30厘米、高25厘米。
现将一块高14厘米,体积为1000立方厘米的假石山放入缸内。如果水龙头以每分5000毫升的流量向鱼缸内注水,那么至少需要多少分钟才能将假石山完全淹没?
41.(23-24五年级下·四川广元·期末)学校放学时,小夏直接走路回家,行程情况统计如下图所示。到家后,小夏倒了一杯纯牛奶,先喝了整杯的,再开始做语文作业,用了小时完成;休息了一会儿,他发现牛奶凉了,就兑满了热水,又喝了半杯后,开始写数学作业,结果比完成语文作业少用了小时。然后,他就愉快地出去玩了。
(1)小夏回家途中的休息时间占路上总时间的几分之几?
(2)小夏回家做作业一共用了多少小时?
(3)在这整个过程中,小夏一共喝了多少杯纯牛奶?
42.(23-24五年级下·四川广元·期末)大理石是重结晶的石灰岩,因最初产地在我国云南大理而得名,主要用于加工成各种形材。当地一家加工厂将一块长60厘米、宽4分米、高32厘米的大理石截成同样大小的正方体(棱长为整厘米数),且没有剩余,截成的正方体的棱长最长是多少?一共可以截成多少个这样的正方体?
43.(23-24五年级下·四川广元·期末)荣老师:“我买一些普通跳绳和计数跳绳,付给您100元。”售货员:“我口算了一下,应该找给您14元。”荣老师:“不对,您肯定算错了。”你能解释一下,荣老师为什么这么肯定售货员算错了吗?
44.(23-24五年级下·四川广元·期末)一个长方体玻璃鱼缸(无盖),量得它的长是8分米,宽是5分米,高是6分米,水深5.4分米。(玻璃厚度忽略不计)
(1)做这个长方体玻璃鱼缸至少需要玻璃多少平方分米?
(2)如果在这个鱼缸里投入一个棱长是3分米的正方体铁块,鱼缸里的水会不会溢出?请你通过计算说明。
(3)如果会溢出,鱼缸里会溢出多少升水?如果不会溢出,现在水深是多少分米?
45.(23-24五年级下·四川凉山·期末)暑假期间玲玲一家准备到西藏自驾游,西昌到西藏拉萨全程两千多千米。玲玲家的越野车油箱从里面量长1米,宽0.4米,高0.2米,油价为7.86元/升,加满一箱油要用多少钱?
46.(23-24五年级下·湖南长沙·期末)张大爷家承包了10亩土地,其中种蔬菜,种粮食,其余种果树。种果树的面积占总面积的几分之几?
47.(23-24五年级下·湖南长沙·期末)刘老师买一种乳酸菌饮料。甲超市价格为15元7盒,乙超市价格为17元8盒,丙超市价格为9元4盒。哪家超市的这种乳酸菌饮料最便宜?
48.(23-24五年级下·湖南长沙·期末)王爷爷有一个长方形的花园,长35米,宽15米。他想把这个花园分成若干个大小相同的正方形区域(正方形边长为整米数)来种植不同的花卉。王爷爷最少可以将花园分成多少个这样的正方形区域?边长是多少米?
49.(19-20五年级上·全国·期末)将7.6立方米的沙子铺在一个长5米、宽38分米的沙坑里,可以铺多厚?
50.(23-24四年级下·河北唐山·期末)工程队修一条路,第一周修了全长的,第二周修了全长的,还剩全长的几分之几没有修?
51.(2024·四川乐山·小升初真题)一个长方体的玻璃缸,长9分米,宽8分米,高6分米,水深4.5分米,如果投入一块棱长为5分米的正方体铁块,缸里的水会溢出吗?如果溢出,会溢出多少升?
52.(2024·四川内江·小升初真题)1路公交车从站过站到站,然后返回,去时在站停车,而返回时到站不停车,去时车速为每小时48千米。
结合图中信息,完成以下问题:
(1)求站到站的路程。
(2)求返回的车速。
53.(2024·福建莆田·小升初真题)学校新修一个游泳池,长25米,宽21米,最浅处水深1.2米,最深处水深1.6米(说明:游泳池底面是倾斜的),如图所示。这个游泳池最多能蓄水多少立方米?
54.(2024·四川乐山·小升初真题)某次跳绳比赛中,选手们每分钟跳绳个数统计图如图所示,仔细观察后,回答下列问题:
(1)每分钟跳绳个数在100个以上(含100个)的选手人数是多少?
(2)每分钟跳绳个数少于100个的选手人数是每分钟跳绳个数在100个以上(含100个)的选手人数的几分之几?
55.(2024·福建宁德·小升初真题)下面是某旅游景点去年接待游客情况统计图。
(1)根据图中的数据,把统计表填写完整。
季度 合计 第一季度 第二季度 第三季度 第四季度
人数/万
(2)平均每月接待游客多少万人?
(3)如果要对这个景点进行整修,根据如图,你觉得选什么时间比较合适?请说明理由。
56.(2024·浙江杭州·小升初真题)一批货物重120吨,运走50吨。运走了几分之几?剩下的占总数的几分之几?
57.(2024·浙江杭州·小升初真题)去年,某厂计划生产一批玩具,结果上半年完成计划的,下半年完成了计划的,该厂去年超额完成了计划的几分之几?
58.(2024·浙江杭州·小升初真题)如表分别是小红和小英两位同学5次跳绳(每次1分钟)情况的统计表和统计图。
小红5次跳绳情况统计表
次数 第1次 第2次 第3次 第4次 第5次
下数(下) 120 113 130 120 135
(1)根据统计表的数据,请在如图的统计图中画出表示小红跳绳情况的折线。
(2)看图解答下面的问题:小英平均每次跳绳多少下?
59.(2024·浙江温州·小升初真题)亮亮利用两种方法测量一块石块的体积。(单位:厘米)
方法一 方法二
(1)这两种方法相同的地方是 。
(2)请选择你喜欢的一种方法计算这块石块的体积。
60.(2024·浙江杭州·小升初真题)小红家有一些鸡蛋,5个5个地数,6个6个地数都多出了2个,已知这些鸡蛋总数在80到100个之间。你能算出小红家有多少个鸡蛋吗?
61.(2024·河南郑州·小升初真题)邮递员小王从县城出发,骑自行车到A村投递,途中遇到县城中学的学生李明从A村步行返校。小王在A村完成投递工作后,返回县城途中又遇到李明,便用自行车载上李明,一起到达县城,结果小王比预计时间晚到1分钟。二人与县城间的距离(千米)和小王从县城出发后所用时间(分)之间的关系如图所示,假设二人之间交流的时间忽略不计,求:
(a)小王和李明第一次遇到时,距县城多少千米?
(b)小王从县城出发到返回县城所用时间是多少?
(c)李明从A村到县城共用多长时间?
62.(2024·重庆丰都·小升初真题)探究与运用。
(1)探究:请你举出“两个相邻奇数相乘的例子”,再观察它们所得积末尾数字的特征。(例子要包含积末尾数字不同的情况)
(2)发现:两个相邻奇数相乘,积末尾数字一定是( )和( )。
(3)运用:下面三个数中,只有一个数是两个相邻奇数的积,它是( )。
A.337 B.1661 C.3363
(4)这两个奇数分别是( )和( )。
63.(2024·浙江杭州·小升初真题)如图所示,图①和图②是两块形状不同的铁皮,将每块铁皮弯折后焊接成一个无盖的长方体铁桶(②号焊接成的是一个底面为正方形的无盖长方体),哪个铁桶的容积更大?
64.(2024·浙江杭州·小升初真题)某小学建一个长方体游泳池,长80米,宽25米,深2米。
(1)在游泳池的底部和四周贴瓷砖,贴瓷砖的面积有多少平方米?
(2)如果在游泳池内注水到1.2米的高度,那么需要注入多少立方米的水?
65.(2024·河北石家庄·小升初真题)如图是一辆公交车从起始站至终点站的行驶过程中乘客上下车情况统计图。
(1)请把统计图中的图例补充完整。
(2)从图中可以看出,第( )站上车乘客和下车乘客一样多,第( )站下车乘客最多。
(3)这辆公交车最多时载( )位乘客。
66.(2024·山东临沂·小升初真题)六(2)班的4名同学观察并测量了一个长方体,得到了5条信息:
信息1:如果高再增加3厘米,那么它恰好是一个正方体。
信息2:长方体的侧面积是280平方厘米。
信息3:长方体的表面积是480平方厘米。
信息4:长方体的棱长总和是108厘米。
信息5:长方体的底面周长是40厘米。
这5条信息都是正确的,请从中选择需要的信息,求出这个长方体的体积。
67.(2024·浙江杭州·小升初真题)一个长方体的长是10厘米,如果将长增加4厘米,则体积增加25立方厘米,那么,原来长方体的体积是多少立方厘米?
68.(2024·浙江杭州·小升初真题)暑假,王老师一家自驾去离家380千米的景点玩,如图是他们离家的距离与汽车行驶时间之间的关系图。
(1)王老师一家出发30分钟时,离家多少千米?
(2)出发后3小时,距离目的地多少千米?
69.(2024·四川绵阳·小升初真题)在下午3:00与4:00之间,求分针与时针成60度角的时间。
70.(2024·浙江湖州·小升初真题)一辆货车从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地。已知甲乙两地的路程是330千米,货车在途中停留半小时。两车离甲地的路程与时间关系如图所示。轿车比货车早几小时到达乙地?
参考答案
1.
【分析】求一个数是另一个数的几分之几用除法计算,据此解答即可。
【解析】21÷37=
答:大龙舟代表队的参赛支数是参赛代表队总支数的。
2.经过公园的路近
【分析】小美家到邮局是千米,邮局到学校是千米;小美家到公园是千米,公园到学校是千米,把这两条路线的长度相加,再比较哪个路程最短即可;计算时根据异分母分数加减法的计算方法,先通分,再按照同分母分数加减法的计算方法计算即可。
【解析】+=+=(千米)
+=+=(千米)
<
答:走经过公园的路比较近。
3.32000÷(32000÷16+32000÷20)
【分析】由题意可知,先根据工作效率=工作总量÷工作时间,分别用32000÷16和32000÷20求出甲、乙的工作效率,再根据工作时间=工作总量÷甲乙合作的工作效率,据此解答即可。
【解析】32000÷(32000÷16+32000÷20)
=32000÷(2000+1600)
=32000÷3600
=(天)
答:如果两组生产线合做,天可以完成。
4.20厘米;12个
【分析】根据题意,裁成的正方形边长最大是多少,就是求80和60的最大公因数,求至少可以裁成多少个这样的正方形,用这张纸的面积除以正方形面积,由此解答即可。
【解析】80=2×2×2×2×5,60=2×2×3×5
80和60的最大公因数是2×2×5=20
即裁成的小正方形的边长最大是20厘米。
(80×60)÷(20×20)
=4800÷400
=12(个)
答:剪出小正方形的边长最大是20厘米,至少可以剪12个这样的小正方形。
5.
【分析】把整节课的时间看作单位“1”,根据分数减法的意义,用1减去老师讲解的时间占的分率,再减去学生小组探究的时间占的分率,即可求出做练习的时间占整节课的分率。
【解析】1--
=1--
=
答:做练习的时间占整节课的。
6.(1)470平方厘米
(2)900立方厘米
【分析】(1)从设计图中可知,这个长方体水槽的长是20厘米,宽是9厘米,高是5厘米,这个水槽的表面积等于五个铁皮的面积和。
(2)长方体的体积=长×宽×高,将数据代入公式计算。
【解析】(1)20×9+20×5×2+5×9×2
=180+200+90
=470(平方厘米)
答:制作这个水槽至少需要铁皮470平方厘米。
(2)20×9×5=900(立方厘米)
答:它的容积有900立方厘米。
7.(1)35;
(2)15;30
(3)35;40
【分析】(1)虚线表示甲飞机数据,实线表示乙飞机数据,观察实线和虚线最右侧数据,即可知道飞行时间;将乙飞机飞行时间看作单位“1”,甲飞机飞行时间÷乙飞机飞行时间=甲飞机飞行时间是乙飞机飞行时间的几分之几;
(2)观察复式折线统计图,两数据点高度一样时,飞行高度一样,两数据点相距越远表示飞行高度相差越大,分别观察横轴相应时间即可;
(3)观察复式折线统计图中的虚线,折线往下坡度越陡,表示飞行高度下降越快,观察横轴对应时间即可。
【解析】(1)40÷35==
乙飞机共飞行了35秒,甲飞机飞行时间是乙飞机飞行时间的。
(2)当飞到第15秒时,两架飞机的飞行高度一样;当飞到第30秒时,两架飞机的飞行高度相差最大。
(3)从第35秒到第40秒,甲飞机的飞行高度下降得最快。
8.(1)见详解
(2)种生菜区域占这块地的几分之几
(3)
【分析】(1)已知这块地的区域种黄瓜,根据分数的意义可知,把这块地的总面积看作单位“1”,平均分成8份,种黄瓜占了其中的3份,据此在图中用斜线表示出种黄瓜的区域。
(2)把这块地的总面积看作单位“1”,算式表示用“1”减去种西红柿区域与种黄瓜区域一共占这块地的分率之和,即是种生菜区域占这块地的几分之几。
(3)先求出种生菜区域占这块地的几分之几,再减去种西红柿区域占这块地的,即是种生菜区域比种西红柿区域多占这块地的几分之几。
【解析】(1)如图:
(2)算式要解决的问题是(种生菜区域占这块地的几分之几)。
(3)
答:种生菜区域比种西红柿区域多占这块地的。
9.256立方厘米
【分析】红薯的体积等于红薯取出前后水变化的体积,水的体积相当于长8厘米、宽为8厘米,高为(14-10)厘米的长方体的体积,长方体体积=长×宽×高,据此列式计算。
【解析】8×8×(14-10)
=64×4
=256(立方厘米)
答:红薯的体积是256立方厘米。
10.
【分析】把参加马拉松比赛的总人数看作单位“1”,求参加半程马拉松的人占总人数的几分之几,用1减去参加全程马拉松的人占总人数的,再减去参加欢乐跑的人占总人数的,据此列式解答。
【解析】1--
=-
=
答:参加半程马拉松的人占总人数的。
11.(1)
(2)
(3)问题:最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的几分之几?
【分析】(1)根据统计表可知,最喜欢冰箱贴的人数占总人数的,最喜欢抱枕的人数占总人数的,用()计算;
(2)最喜欢钥匙扣的人数占总人数的,最喜欢水杯的人数占总人数的,用()计算;
(3)可以提问一个与最喜欢钥匙扣的人数相关的问题:如最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的几分之几?(答案不唯一)
【解析】(1)
答:最喜欢冰箱贴和抱枕的人数共占总人数的。
(2)
答:最喜欢钥匙扣的比水杯的人数多占总人数的。
(3)问题:最喜欢冰箱贴的比最喜欢钥匙扣的多占总人数的几分之几?
答:最喜欢冰箱贴的比最喜欢钥匙扣的人数多占总人数的。
12.(1)可以
(2)8800平方厘米
【分析】(1)把张阿姨行李箱的长、宽、高与免费托运行李限制的长、宽、高进行比较,如果小于或等于免费托运行李限制的尺寸,就可以免费托运;反之,不可以免费托运。
(2)根据题意,给这个行李箱加个布套(底面不做),即做布套的面是长方体的上面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是这个布套至少需要布料的面积。
【解析】(1)40<60,25<40,60<100
张阿姨的行李可以免费托运。
可以 不可以
(2)40×25+40×60×2+25×60×2
=1000+4800+3000
=8800(平方厘米)
答:这个布套至少需要8800平方厘米布料。
13.10时40分
【分析】从图中可知,65路公交车每20分钟一班,95路公交车每25分钟一班,那么这两车同时到站的时间间隔是20、25的最小公倍数,再加上第一次同时到站的时刻,就是下一次这两路公交车同时到站的时刻。
【解析】20=2×2×5
25=5×5
20和25的最小公倍数是2×2×5×5=100;
即每100分钟这两路公交车同时到站。
100分钟=1时40分
9时+1时40分=10时40分
答:下一次这两路公交车同时到“学府街关林路口”公交车站是10时40分。
14.(1)
(2)5月23日
【分析】(1)把全书的总页数看作单位“1”,聪聪第一天、第二天分别看了全书的、,根据减法的意义,用“1”减去第一天、第二天看了全书的分率,即是还剩这本书的几分之几没有看。
(2)已知睿睿每3天去一次,敏敏每5天去一次,他们在图书馆相遇的间隔天数就是3和5的最小公倍数;先求出3和5的最小公倍数,再加上他们上一次在图书馆相遇的日期,即是下次在图书馆相遇的日期。
【解析】(1)1--
=-
=-
=
答:还剩这本书的没有看。
(2)3和5的最小公倍数是:3×5=15
即每15天两人在图书馆相遇。
5月8日+15日=5月23日
答:他们下次在图书馆相遇是5月23日。
15.850平方厘米
【分析】根据题意,王老师制作这套图书的封套包裹了书的上下面、左右面和后面共5个面,根据“长×宽×2+宽×高×2+长×高”求出这5个面的面积之和,即是至少需要硬纸板的面积。
【解析】5×15×2+15×20×2+5×20
=150+600+100
=850(平方厘米)
答:至少需要850平方厘米的硬纸板。
16.(1)1700平方米
(2)56.96立方米
【分析】(1)由题可知,要在“水立方”游泳池四壁和底面贴瓷片,则贴瓷片的面积等于游泳池五个面的面积之和(除去上面),根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,进行计算即可;
(2)根据长方体的体积公式:体积=长×宽×高,据此求出一条赛道需要用的冰的体积,再乘4即可,注意单位名数的统一。
【解析】(1)50×25+(50×3+25×3)×2
=1250+(150+75)×2
=1250+225×2
=1250+450
=1700(平方米)
答:贴瓷片的面积至少是1700平方米。
(2)8厘米=0.08米
44.5×4×0.08×4
=178×0.08×4
=14.24×4
=56.96(立方米)
答:一共需要用冰大约56.96立方米。
17.
【分析】以月球土壤总量为单位“1”,用单位“1”减去氧、硅、铁的分率,即可得其它成分占月球土壤成分的分率。
【解析】1---
=---
=
答:其它成分占月球土壤成分的。
18.7800立方厘米
【分析】这个亚当牛尊工艺品的体积等于上升的这部分水的体积,根据长方体的体积=长×宽×高,用长方体容器的底面积乘水上升的高度,计算出上升这部分水的体积,也就是这个亚当牛尊工艺品的体积。
【解析】65×40×(15-12)
=2600×3
=7800(立方厘米)
答:亚当牛尊工艺品的体积是7800立方厘米。
19.15000立方厘米
【分析】根据题意可知,水面上升的部分的体积就是珊瑚的体积,根据长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】50×30×10
=1500×10
=15000(立方厘米)
答:珊瑚的体积是15000立方厘米。
20.土豆的体积是144立方厘米,红薯的体积是240立方厘米。
【分析】放入物体后,上升的水的体积就是物体的体积,根据,放入土豆后,水面上升了厘米,上升的水的体积就是土豆的体积;放入红薯水面上升了厘米,上升的水的体积就是红薯的体积。代入数据计算即可得解。
【解析】土豆的体积:
(立方厘米)
红薯的体积:
(立方厘米)
答:土豆的体积是144立方厘米,红薯的体积是240立方厘米。
21.(1)576平方厘米
(2)1296立方厘米
【分析】(1)贴彩纸的面积=长方形纸板的面积-4个正方形的面积,长方形面积=长×宽,正方形面积=边长×边长,据此列式解答;
(2)长方体的长=长方形的长-正方形边长×2,长方体的宽=长方形的宽-正方形边长×2,长方体的高=正方形的边长,根据长方体容积=长×宽×高,列式解答即可。
【解析】(1)30×24-6×6×4
=720-144
=576(平方厘米)
答:贴彩纸的面积是576平方厘米。
(2)30-6×2
=30-12
=18(厘米)
24-6×2
=24-12
=12(厘米)
18×12×6=1296(立方厘米)
答:这个盒子的容积是1296立方厘米。
22.864立方米
【分析】根据长方体体积=长×宽×高,求出一个水池的容积,再乘2即可,注意统一单位。
【解析】20厘米=0.2米
90×24×0.2×2
=432×2
=864(立方米)
答:需要注入864立方米的水。
23.5.36平方米
【分析】求展示罩的面积相当于求长方体表面积,因为无底,展示罩的面积=长×宽+长×高×2+宽×高×2,据此列式解答。
【解析】
(平方米)
答:制作一个这样透明展示罩需要5.36平方米的材料。
24.小时
【分析】求参观这三个馆一共用了多长时间,就是求小时、小时、小时的和,列分数连加法算式解答。
【解析】
(小时)
答:小明参观这三个馆一共用了小时。
25.0.63元
【分析】由于⑤和①是正方形,当一个长方体有两个面是正方形,其他四个侧面是一样的长方形,通过图可知,长是6厘米,那么宽也是6厘米,高是3厘米,通过图可知,缺少了一个长是6厘米,宽是3厘米的长方形的面;根据正方形的面积公式:边长×边长,求出一个正方形的面积再乘2,长方形的面积:长×宽,求出一个长方形的面积再乘3,把这两部分相加即可求出这个无盖纸盒的表面积,根据1平方米=10000平方厘米,转换单位,再用表面积乘每平方米的价钱,即可求出需要的总钱数。
【解析】6×6×2+6×3×3
=72+54
=126(平方厘米)
126平方厘米=0.0126平方米
0.0126×50=0.63(元)
答:做这个纸盒至少需要0.63元。
26.;
【分析】将这条路的全长看作单位“1”,第一周修的长度÷全长=第一周修了这条路的几分之几;1-第一周修了这条路的几分之几-第二周修了这条路的几分之几=还剩几分之几没有修,据此列式解答。
【解析】500÷1500==
1--
=-
=-
=
答:工程队第一周修了这条路的,两周后这条路还剩没有修。
27.8厘米
【分析】根据正方体棱长总和=棱长×12,求出铁丝长度,再根据长方体的高=棱长总和÷4-长-宽,列式解答即可。
【解析】10×12÷4-14-8
=120÷4-14-8
=30-14-8
=16-8
=8(厘米)
答:长方体框架的高是8厘米。
28.3分钟
【分析】先确定把假山完全淹没需要的水的体积,即为长、宽、高分别为6分米、4分米、1.5分米的水的体积再减去假山的体积,求出需要注水的体积,又知道每分钟注水量,再根据:时间=总量÷速度,用需要注水的体积除以10立方分米即可解答。
【解析】(6×4×1.5-6)÷10
=(24×1.5-6)÷10
=(36-6)÷10
=30÷10
=3(分钟)
答:至少需要3分钟才能把假山石刚好淹没。
29.吨
【分析】由题意可知,储存小米的质量=储存大米的质量-吨,储存面粉的质量=储存小米的质量+0.4吨,据此解答。
【解析】-+0.4
=-+
=+-
=1-
=(吨)
答:这个仓库储存了吨面粉。
30.160平方分米
【分析】由图可知,相交于同一顶点的3条棱的长度分别是4分米、4分米、8分米,根据“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个长方体的表面积,据此解答。
【解析】(4×4+4×8+4×8)×2
=(16+32+32)×2
=80×2
=160(平方分米)
答:这个长方体的表面积是160平方分米。
31.24升
【分析】求缸里的水会溢出多少,就是求正方体铁块的体积比长方体玻璃水缸还能容纳物体的体积多多少,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,分别求出正方体铁块的体积和长方体玻璃水缸还能容纳物体的体积,再用正方体铁块的体积减去长方体玻璃水缸还能容纳物体的体积,求出缸里的水溢出多少立方分米,再根据1立方分米=1升,把立方分米化为升即可解答。
【解析】4×4×4-8×5×(5-4)
=16×4-40×1
=64-40
=24(立方分米)
24立方分米=24升
答:缸里的水会溢出24升。
32.(1)23;30;
(2)上升;
(3)小林同学;见详解
【分析】(1)复式折线统计图中,横轴表示时间,纵轴表示数量,实线表示小林一周每天一分钟跳绳的情况,虚线表示小丽一周每天一分钟跳绳的情况,折点位置越高跳绳数量越多,折点位置越低跳绳数量越少;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线走势向上总体呈现上升趋势,折线走势向下总体呈现下降趋势;
(3)从两条折线的走势分析两位同学的跳绳情况,选择成绩波动较小且呈上升趋势的同学即可。
【解析】(1)小林:218-195=23(个)
小丽:223-193=30(个)
所以,小林同学一分钟跳绳的最高成绩与最低成绩相差23个,小丽同学一分钟跳绳的最高成绩与最低成绩相差30个。
(2)从图中可知,小林同学跳绳的成绩,总体呈现上升趋势。
(3)推荐小林同学,观察复式折线统计图可知,小丽的成绩波动较大,小林的成绩稳定且整体呈现上升趋势。(答案不唯一)
33.
【分析】先求出这第二天一共卖的箱数,再除以矿泉水的总箱数,即是这两天一共卖了所有矿泉水的几分之几。
【解析】12+20=32(箱)
32÷96=
答:两天一共卖了所有矿泉水的。
34.
【分析】将总时间看作单位“1”,1-往返路上用去的时间占总时间的几分之几-休息的时间占总时间的几分之几=参观学习时间占总时间的几分之几。
【解析】1--
=-
=-
=
=
答:参观学习时间占总时间的。
35.(1)二
(2)六;10
(3)B款;理由见详解
【分析】(1)观察复式折线统计图,当两条折线相交于一点时,说明这一天两款扫地机器人的清扫时长相同。
(2)观察复式折线统计图,当两条折线的叉口最大时,说明两款扫地机器人的清扫时长相差最大,再用减法求出相差的时间。
(3)在两款扫地机器人清扫效果大致相同的情况下,选择清扫时长较短的扫地机器人更合适,说明理由,合理即可。
【解析】(1)试验第二天,两款扫地机器人的清扫时长相同。
(2)16-6=10(分钟)
试验第六天,两款扫地机器人的清扫时长相差最大,相差10分钟。
(3)如果两款扫地机器人清扫效果大致相同,该公司会批量生产B款扫地机器人,因为随着清扫天数的增加,B款清扫用时逐渐减少且趋于平稳,说明它更智能、更省电。
36.35人
【分析】他们的绘画作品平均分成6组或10组,都多5幅,由此可知,他们的作品的总数量减去5就是6和10的公倍数,由于每人限投一幅作品,则五(1)班至少人数是6和10的最小公倍数,再加上5,根据求两个数最小公倍数的方法:两个数的公有质因数与每一个独有质因数连乘积,就是最小公倍数,如果两个数为倍数关系,则最小公倍数为较大的数,如果两个数为互质数,则最小公倍数为两个数的乘积,据此解答。
【解析】6=2×3
10=2×5
6和10的最小公倍数是2×3×5=30
30+5=35(人)
答:五(1)班至少有35人参与投稿。
37.2000平方分米
【分析】由题意可知,240分米是正方体的棱长总和,根据的逆运算,用240除以12可得棱长,再根据正方体表面积的特征,用棱长乘棱长乘5,即可得解。
【解析】(分米)
(平方分米)
答:至少需要2000平方分米的彩纸。
38.15.625吨
【分析】根据题意,水箱是一个铁皮做成的棱长25分米的无盖正方体,根据正方体的体积(容积)公式V=a3,求出水箱的容积,再根据进率“1立方米=1000立方分米”换算单位;然后用每立方米水的重量乘水箱的容积,即可求出这个水箱能装水的总重量。
【解析】25×25×25
=625×25
=15625(立方分米)
15625立方分米=15.625立方米
1×15.625=15.625(吨)
答:这个水箱能装水15.625吨。
39.12.9平方米
【分析】已知牛奶盒长6厘米、宽4厘米、高10.5厘米,根据长方体的表面积=(长×宽+长×高+宽×高)×2,求出1个牛奶盒的表面积,再乘500,即是做500个这样的纸盒至少需要硬纸板的面积。注意单位的换算:1平方米=10000平方厘米。
【解析】(6×4+6×10.5+4×10.5)×2
=(24+63+42)×2
=129×2
=258(平方厘米)
258×500=129000(平方厘米)
129000平方厘米=12.9平方米
答:做500个这样的纸盒至少需要12.9平方米的硬纸板。
40.4分钟
【分析】根据题意,要将一块高14厘米,体积为1000立方厘米的假石山完全淹没,那么要向长方体鱼缸内注入14厘米高的水;根据长方体的体积=长×宽×高,求出将假石山完全浸没水和假山石的体积之和,再减去假山石的体积,即是需注入水的体积;然后根据进率“1立方厘米=1毫升”换算单位;
已知水龙头以每分5000毫升的流量向鱼缸内注水,用注入水的体积除以水的流速,即可求出时间。
【解析】50×30×14
=1500×14
=21000(立方厘米)
21000-1000=20000(立方厘米)
20000立方厘米=20000毫升
20000÷5000=4(分钟)
答:至少需要4分钟才能将假石山完全淹没。
41.(1);
(2)小时;
(3)杯
【分析】(1)根据统计图可知,小夏休息时间用了(15-5)分钟,总时间是25分钟;用小夏休息时间除以总时间,即可求出小夏回家途中的休息时间占路上总时间的分率;
(2)用小夏完成语文作业的时间-小时,求出小夏完成数学作业的时间,再加上完成语文作业时间,即可求出小夏回家做作业一共用时间;
(3)把这杯牛奶的总量看作单位“1”,先喝了整杯的,即喝了杯;用1-=杯,求出剩下牛奶的量,他发现牛奶凉了,就兑满了热水,又喝了半杯,实际上喝了杯的一半,杯的一半是杯,用先喝的杯再加上杯,即可求出小夏一共喝了多少杯纯牛奶。
【解析】(1)(15-5)÷25
=10÷25
=
答:小夏回家途中的休息时间占路上总时间的。
(2)-+
=-+
=+
=(小时)
答:小夏回家做作业一共用了小时。
(3)1-=(杯)
杯的一半是杯。
+=(杯)
答:小夏一共喝了杯。
42.4厘米;1200个
【分析】4分米=40厘米,由题意可知,求截成的正方体的棱长最长是多少,就是求60、40、32的最大公因数,先把60、40、32分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数;用60、40、32分别除以它们的最大公因数,再把它们的商相乘即可解答。
【解析】4分米=40厘米
60=2×2×3×5
40=2×2×2×5
32=2×2×2×2×2
60、40、32的最大公因数是2×2=4
所以正方体棱长最长是4厘米;
(60÷4)×(40÷4)×(32÷4)
=15×10×8
=150×8
=1200(块)
答:截成的正方体的棱长最长是4厘米,一共可以截成1200个这样的正方体。
43.见详解
【分析】根据5的倍数特征:个位上是0或5的数,都是5的倍数;因为跳绳的单价是5元,计数跳绳的单价是10元;10是5的倍数,所以无论买多少根跳绳和计数跳绳,那么花的钱数和找回的钱数一定是5的倍数,据此解答。
【解析】100-14=86(元)
根据两种跳绳单价可知,荣老师花的钱数应是5的倍数,找回的钱数也是5的倍数,但是花的钱数86不是5的倍数,找回的钱数14也不是5的倍数,所以荣老师这么肯定售货员算错了。
44.(1)196平方分米
(2)会溢出;见详解
(3)3升
【分析】(1)从图中可知:这个长方体的长是8分米,宽是5分米,高是6分米。这个无盖的长方体有下面和前后左右面共5个面,因此需要玻璃的面积= 长×宽+长×高×2+宽×高×2,代入数据计算即可。
(2)此时水深5.4分米,还剩下空间的高度6-5.4=0.6分米,根据长方体的体积(容积)=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据计算,分别求出剩下空间的容积、正方体的体积,再比较即可。
(3)若溢出,用正方体的体积减去剩下空间的容积,即可求出溢出的水量(换算成以升为单位);若不会溢出,用正方体的体积÷长方体的底面积,求出正方体放入水中后,水面升高的高度,再加上原来的水面高度,即可求出现在的水面高度。
【解析】(1)8×5+8×6×2+5×6×2
=40+96+60
=196(平方分米)
答:做这个长方体玻璃鱼缸至少需要玻璃196平方分米。
(2)3×3×3=27(立方分米)
8×5×(6-5.4)
=8×5×0.6
=24(立方分米)
27>24
答:鱼缸里的水会溢出。
(3)27-24=3(立方分米)
3立方分米=3升
答:鱼缸里会溢出3升水。
45.628.8元
【分析】根据长方体的体积=长×宽×高,代入数据求出油箱的容积,进而根据1立方米=1000升换算成升,再根据单价×数量=总价,用油箱的升数乘7.86即可求出加满这箱油要多少钱。
【解析】1×0.4×0.2=0.08(立方米)
0.08立方米=80升
80×7.86=628.8(元)
答:加满一箱油要用628.8元。
46.
【分析】把承包的10亩土地看作整体“1”,用“1”减去种蔬菜和种粮食的面积占总面积的分率和,即可得解。
【解析】1-(+)
=1-(+)
=1-
=
答:种果树的面积占总面积的。
47.乙超市
【分析】根据总价÷数量=单价,分别计算出三家超市1盒乳酸菌饮料的钱数,比较即可。根据分数与除法的关系表示出结果,即分数的分子相当于被除数,分母相当于除数,再将假分数化成带分数,即可比较出大小。假分数化带分数:用分子除以分母,当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【解析】15÷7==(元)
17÷8==(元)
9÷4==(元)
<<
答:乙超市的这种乳酸菌饮料最便宜。
48.21个;5米
【分析】要想将花园分成的正方形区域越少,分成的正方形就要尽可能的大。求出长方形长和宽的最大公因数,是分成的最大正方形的边长,长方形面积=长×宽,正方形面积=边长×边长,长方形面积÷正方形面积=分成的正方形个数,据此列式解答。
【解析】35=5×7
15=3×5
35和15的最大公因数是5,因此正方形边长是5米。
35×15÷(5×5)
=525÷25
=21(个)
答:王爷爷最少可以将花园分成21个这样的正方形区域,边长是5米。
49.0.4米
【分析】先统一单位,然后根据长方体的高=体积÷长÷宽,代入数据即可解答。
【解析】38分米=3.8米
7.6÷5÷3.8
=1.52÷3.8
=0.4(米)
答:可以铺0.4米厚。
50.
【分析】将这条路的全长看作单位“1”,用单位“1”依次减去第一周和第二周修的占全长的分率,即可求出剩下没修的占全长的几分之几。
【解析】1--
=-
=
=
答:还剩全长的没有修。
51.会溢出;17升
【分析】根据长方体体积公式:体积=长×宽×高;先求出高是(6-4.5)分米空白体积,再根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体铁块的体积,再用高是(6-4.5)分米空白部分体积与正方体铁块的体积比较,如果高是(6-4.5)分米空白部分的体积大于正方体铁块的体积,水不会溢出;如果高是(6-4.5)分米空白部分的体积小于正方体铁块的体积,水会溢出,再用正方体铁块的体积-高是(6-4.5)分米空白部分的体积,即可求出溢出的水的体积,注意单位名数的换算。据此解答。
【解析】9×8×(6-4.5)
=72×1.5
=108(立方分米)
5×5×5
=25×5
=125(立方分米)
125>108
125-108=17(立方分米)
17立方分米=17升
答:缸里的水会溢出,溢出17升。
52.(1)3.2千米;(2)72千米
【分析】(1)由图上发现,从到用了4分钟,根据路程速度时间可,以求出站到站的路程。
(2)发现回来一共用了6分钟,去的时候从到一共用了5分钟,可以求出到的路程,再加上站到站的路程即可求出总路程,用路程时间速度,可以求出返回的速度。
【解析】(1)48千米时千米分
(千米)
答:站到站的路程是3.2千米。
(2)(分钟)
(千米)
(分钟)
(千米)
1.2×60=72(千米)
答:返回的车速是每小时72千米。
53.735立方米
【分析】观察题意可知,以梯形的一面为底面,首先根据梯形的面积公式:S=(a+b)h÷2,求出底面积,然后根据体积=底面积×高,即可求出这个游泳池最多能蓄水的多少立方米。
【解析】(1.2+1.6)×25÷2×21
=2.8×25÷2×21
=35×21
=735(立方米)
答:这个游泳池最多能蓄水735立方米。
54.(1)22人
(2)
【分析】(1)从条形统计图中可知,每分钟跳绳个数在100~109个的选手有15人,每分钟跳绳个数在110~120个的选手有7人,用加法计算,即可求出每分钟跳绳个数在100个以上(含100个)的选手人数。
(2)先用加法求出每分钟跳绳个数少于100个的选手人数,再除以每分钟跳绳个数在100个以上(含100个)的选手人数即可,结果用最简分数表示。
【解析】(1)15+7=22(人)
答:每分钟跳绳个数在100个以上(含100个)的选手人数是22人。
(2)(5+6+9)÷22
=20÷22
=
答:每分钟跳绳个数少于100个的选手人数是每分钟跳绳个数在100个以上(含100个)的选手人数的。
55.(1)18;2.5;5;6;4.5
(2)1.5万人
(3)第一季度,理由见解析
【分析】(1)观察折线统计图可知,横轴表示季度,纵轴表示人数,据此读取各季度数据填空,再把四个季度的人数相加即可得合计人数。
(2)一年有12个月,根据求平均数用除法计算,用合计人数除以12即可得解。
(3)应选择景点人数最少的季度进行整修,才不耽误旺季的营业。
【解析】(1)2.5+5+6+4.5=18(万人)
如表所示
季度 合计 第一季度 第二季度 第三季度 第四季度
人数/万 18 2.5 5 6 4.5
(2)18÷12=1.5(万人)
答:平均每月接待游客1.5万人。
(3)
答:应该在旅游人数最少的第一季度整修,这样不耽误旺季的营业。
56.;
【分析】用运走的质量除以货物的总质量,求出运走了几分之几;再把货物的总质量看作单位“1”,利用单位“1”减去运走的几分之几就是剩下的几分之几,据此解答。
【解析】
1-=
答:运走了,剩下的占总数的。
57.
【分析】把全年计划看作单位“1”,首先用某长上半年完成计划的分率加上下半年完成计划的分率,求出某长全年一共完成了计划的几分之几;然后用它减去1,求出该厂去年超额完成了计划的几分之几即可。
【解析】+-1
=-1
=
答:该厂去年超额完成了计划的。
58.(1)见详解
(2)121下
【分析】(1)根据统计表中小红跳绳的情况多少,先在图中描出各点,然后用线段顺次把各点连接起来即可。
(2)用小英5次跳的下数之和除以5即可解答。
【解析】(1)如下图所示:
(2)(115+113+120+127+130)÷5
=605÷5
=121(下)
答:小英平均每次跳绳121下。
59.(1)都是应用排水法测量实物的体积
(2)1570立方厘米
【分析】(1)方法一和方法二都是利用水的体积变化来测量石块的体积。方法一是通过测量放入石块前后水的高度变化,计算出石块的体积;方法二是通过测量溢出的水的体积来直接得到石块的体积。这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法。把石块放入有水的长方体容器中,石块完全浸没在水里(水未溢出),上升部分水的体积就等于石块的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
第②种实验方法。把石块放在盛满水的容器里,石块完全浸没在水里,水溢出来,把溢出来的水倒入圆柱体容器里,溢出的水的体积就等于石块的体积,根据圆柱体的体积公式:V=Sh(S=πr2),把数据代入公式解答。
【解析】(1)这两种方法相同的地方是:都是应用排水法测量实物的体积。(合理即可)
(2)第①种实验方法:
20×15.7×(15-10)
=314×5
=1570(立方厘米)
第②种实验方法:
3.14×52×20
=3.14×25×20
=78.5×20
=1570(立方厘米)
这块石块的体积是1570立方厘米。
(选择其一即可)
60.92个
【分析】根据题意,一些鸡蛋,5个5个地数,6个6个地数都多出了2个,说明这些鸡蛋的总个数比5和6的公倍数还多2;
先求出5和6的最小公倍数,再找出在80到100之间的公倍数,最后再加上2个,即是这些鸡蛋的总个数。
【解析】5和6的最小公倍数是:5×6=30
30在80到100之间的公倍数是:30×3=90
90+2=92(个)
答:小红家有92个鸡蛋。
61.(a)4千米
(b)85分钟
(c)105分钟
【分析】从图中可以看出小王和李明并不是同时出发的,小王还有在A村停留时间30分钟,小王去A村和返回速度不一样,这些都可以从图中看出来。
(a)从图中可以看出小王30分时走了6千米,相遇时走了20分,根据、代入数据先求速度,再求路程即可。
(b)小王从县城出发到返回县城所用时间,从图中可以看出包括去时用的时间加在A村待的时间加上返回遇李明的时间加上原计划时间再加上晚到1分钟。
(c)李明从A村到县城共用时间包括自己走路用的时间和小王带他的时间。
【解析】(a)
(千米)
答:小王和李明第一次遇到时,距县城4千米。
(b)小王30分钟到A村休息30分钟返回在离县城1千米和李明相遇,用时20分钟。
返回时小王速度(6-1)÷20
=5÷20
=0.25(千米)
照原速度小王1÷0.25=4(分钟)
那么小王用时=30+30+20+4+1=85(分钟)
(c)李明从图中可以看出从离城5千米到1千米用时80分钟
李明的速度(5-1)÷80
=4÷80
=0.05(千米)
李明从A村和小王第二次相遇用时:5÷0.05=100(分钟)
李明从A村总用时=100+5=105(分钟)
答:从图中可以看出相遇时离县城4千米,小王从县城出发到返回县城所用时间是85分钟,李明从A村到县城共用105分钟。
62.(1)见详解
(2) 3、5 9
(3)C
(4) 59 57
【分析】不是2的倍数的数叫作奇数;通过举例观察两个相邻奇数相乘所得积末尾数字的特征,利用该特征解决后续问题。
【解析】(1)例子:3×5=15,积末尾数字是5;5×7=35,积末尾数字是5;7×9=63,积末尾数字是3;9×11=99,积末尾数字是9;11×13=143,积末尾数字是3。
(2)从上面所举例子可以发现:两个相邻奇数相乘,积末尾数字一定是3和5和9。
(3)A.337末尾数字是7,不符合积末尾数字是3、5、9的特征,所以337不是两个相邻奇数的积。
B.1661末尾数字是1,不符合积的末尾数字是3、5、9的特征,所以1661不是两个相邻奇数的积。
C.3363末尾数字是3,符合积的末尾数字的特征,所以它是两个相邻奇数的积。
(4)因为两个相邻奇数相差2,设较小奇数为x,则较大奇数为x+2,那么x(x+2)=3363
对3363分解质因数,3363=3×19×59=57×59,所以这两个奇数分别是57和
59。.
63.②号
【分析】根据题意,结合图形,先分别求出图①和图②每个长方体的长、宽、高,再根据:长方体的体积(容积)=长×宽×高,分别求出两个长方体铁桶的容积,然后进行比较,即可得出结论。
【解析】图①:110-60=50(厘米)
120-50-50=20(厘米)
60×20×50
=1200×50
=60000(立方厘米)
图②:120÷4=30(厘米)
100-30=70(厘米)
30×30×70
=900×70
=63000(立方厘米)
因为63000立方厘米>60000立方厘米
所以②号铁桶的容积更大。
答:②号铁桶的容积更大。
64.(1)2420平方米;(2)2400立方米
【分析】(1)游泳池是无盖的,所以贴瓷砖的面积是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式:S=ab+2ah+2bh,把数据代入公式求出这5个面的总面积即可。
(2)根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【解析】(1)80×25+80×2×2+25×2×2
=2000+320+100
=2420(平方米)
答:贴瓷砖的面积有2420平方米。
(2)80×25×1.2=2400(立方米)
答:需要注入2400立方米的水。
65.见解答
【分析】(1)观察图例可见,一条实线随站次变化,表示每站“上车”人数;另一条虚线则表示“下车”人数,故应将图例补充为“上车人数”“下车人数”。
(2)从图中读数比较,可发现只有在第六站时,上车人数与下车人数相同;而虚线在第八站达到最高值,说明第八站下车人数最多。
(3)要求“最多时车上有多少乘客”,只需逐站累加(上车人数减下车人数)即可。
【解析】(1)如图:
;
(2)第六站实线与虚线相交,表示上、下车乘客一样多;第八站下车乘客最多;
(3)起始站有2位
第一站:2+9-1=10(位)
第二站:10+11-7=14(位)
第三站:14+12-8=18(位)
第四站:18+10-8=20(位)
第五站:20+13-10=23(位)
第六站:23+14-14=23(位)
第七站:23+13-15=21(位)
第八站:21+12-16=17(位)
第九站:17-13+5=9(位)
23=23>21>20>18>17>14>10>9;最多时载23位乘客。
这辆公交车最多时载23位乘客。
66.见详解
【分析】根据信息1和信息5可知,这个长方体的底面是正方形;根据正方形周长公式:周长=边长×4,边长=周长÷4,据此求出长方体的长和宽,再用边长-3厘米,求出长方体的高,再根据长方体的体积公式:体积=长×宽×高,代入数据,即可解答。
【解析】选择信息1和信息5。
40÷4=10(厘米)
10-3=7(厘米)
10×10×7
=100×7
=700(立方厘米)
答:这个长方体的体积是700立方厘米。
67.62.5立方厘米
【分析】根据长方体的体积=长×宽×高,宽和高不变,长增加4厘米,则增加后长方体的体积=(长+4)×宽×高,原来长方体的体积=长×宽×高。已知将长增加4厘米,体积增加25立方厘米,由增加后的体积-原来的体积=25,代入数值计算出长方体的宽和高的乘积,最后用宽和高的乘积乘原来的长,所得结果即为原来长方体的体积。
【解析】(长+4)×宽×高-长×宽×高=25
化简得:宽×高×4=25
因此宽×高=25÷4=6.25
原来长方体体积:6.25×10=62.5(立方厘米)
答:原来长方体的体积是62.5立方厘米。
68.(1)40千米
(2)130千米
【分析】折线统计图的横轴代表的是时间,纵轴代表的路程,根据折线统计图可以知道王老师2.5小时行驶了200千米,4小时行驶了350千米。
(1)求王老师一家前2.5小时的速度列式:200÷2.5;求后面(4-2.5)小时的速度列式:(350-200)÷(4-2.5);
要想求出“他们出发30分钟时,离家多少千米?”就要知道此时行驶的速度,再根据路程=速度×时间即可解答,注意要把30分钟转换成小时;
(2)先求出后面(4-2.5)小时的速度,求出后面(4-2.5)小时行驶的路程。王老师2.5小时行驶了200千米,用后面(4-2.5)小时行驶的路程加上200千米,计算出前3个小时的行驶路程,总路程减去已行驶的路程即为距离目的地多少千米。
【解析】(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米。
(2)(350-200)÷(4-2.5)×(3-2.5)
=150÷1.5×0.5
=50(千米)
380-(200+50)
=380-250
=130(千米)
答:离目的地还有130千米。
69.3时分和3时分
【分析】时针每分钟走(度),分针每分钟走(度),因此分针每分钟比时针多走(度),3点时,时针在分针前方90度,因此两针夹角为60度时,分针要比时针多走(度),或者多走(度)。分别用30除以5.5,150除以5.5,即可得解。
【解析】(30×3-60)÷(6-0.5)
=(90-60)÷5.5
=30÷5.5
=(分)
(30×3+60)÷(6-0.5)
=150÷5.5
=(分)
答:在钟表上,3点倒4点之间,3时分和3时分时分针与时针成60度的角。
【点睛】本题主要考查分数和除法的关系以及追及问题,关键是求出时针和分针每分钟走的度数。
70.1.2小时
【分析】通过观察统计图可知,货车在(3-0.5)小时内行驶了150千米,根据速度=路程÷时间,可以先求出货车的速度,同时可以计算出货车行驶90千米所用的时间即a的值是1.5小时。
那么轿车在(3-1.5)小时内行驶150千米,根据速度=路程÷时间,可以求出轿车的速度。
最后再根据时间=路程÷速度,分别求出货车、轿车到达乙地各用多少小时,并根据求一个数比另一个少多少,用减法解答。
【解析】货车速度:150÷(3-0.5)
=150÷2.5
=60(千米/时)
a:90÷60=1.5(小时)
轿车速度:150÷(3-1.5)
=150÷1.5
=100(千米/时)
330÷60=5.5(小时)
330÷100=3.3(小时)
5.5+0.5-3.3-1.5
=6-3.3-1.5
=1.2(小时)
答:轿车比货车早1.2小时到达乙地。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
