2025新湘教版七年级数学下册期末综合素质评价试卷(含答案)
文档属性
| 名称 | 2025新湘教版七年级数学下册期末综合素质评价试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览



文档简介
2025新湘教版七年级数学下册期末综合素质评价试卷
一、选择题(每题3分,共30分)
1.浪费不以量小而为之,节约不以微小而不为.下列倡导节约能耗的图标中,文字上方的部分是轴对称图形的是( )
A. B.
C. D.
2.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
3.若与是同一个数的两个不相等的平方根,则这个数是( )
A.3 B. C.16 D.9
4.如图,在边长为9的正方形中放置两个长和宽分别为,的长方形,若长方形的周长为24,面积为,则图中阴影部分的面积为( )
(第4题)
A.18.5 B.21.5 C.27.5 D.35.5
5.已知关于 的不等式 有且只有1个负整数解,则 的取值范围是( )
A. B.
C. D.
6.如图,在锐角三角形 中,,的面积为10,平分,若,分别是,上的动点,则 的最小值为( )
(第6题)
A.4 B.5 C.4.5 D.6
7.如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , ,则 的度数为( )
(第7题)
A. B. C. D.
8.若,则 的值为( )
A.3 B. C. D.
9.已知 是25的平方根,是 的小数部分,则 的值是( )
A.3 B. C.3或 D.
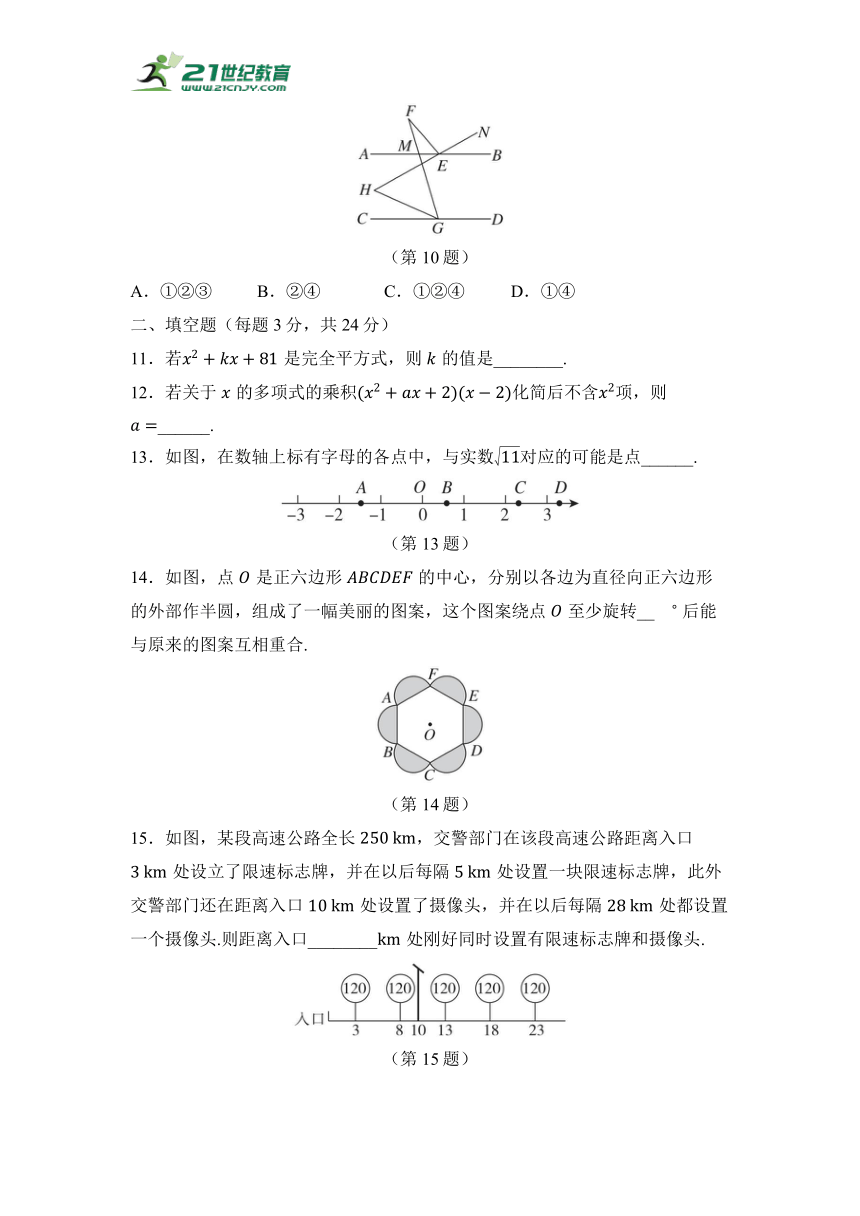
10.如图,与交于点,点在直线上,,,,下列四个结论:
;;
; .
其中正确的是( )
(第10题)
A.①②③ B.②④ C.①②④ D.①④
二、填空题(每题3分,共24分)
11.若是完全平方式,则的值是________.
12.若关于的多项式的乘积化简后不含项,则______.
13.如图,在数轴上标有字母的各点中,与实数对应的可能是点______.
(第13题)
14.如图,点是正六边形的中心,分别以各边为直径向正六边形的外部作半圆,组成了一幅美丽的图案,这个图案绕点至少旋转__ 后能与原来的图案互相重合.
(第14题)
15.如图,某段高速公路全长,交警部门在该段高速公路距离入口处设立了限速标志牌,并在以后每隔处设置一块限速标志牌,此外交警部门还在距离入口处设置了摄像头,并在以后每隔处都设置一个摄像头.则距离入口________处刚好同时设置有限速标志牌和摄像头.
(第15题)
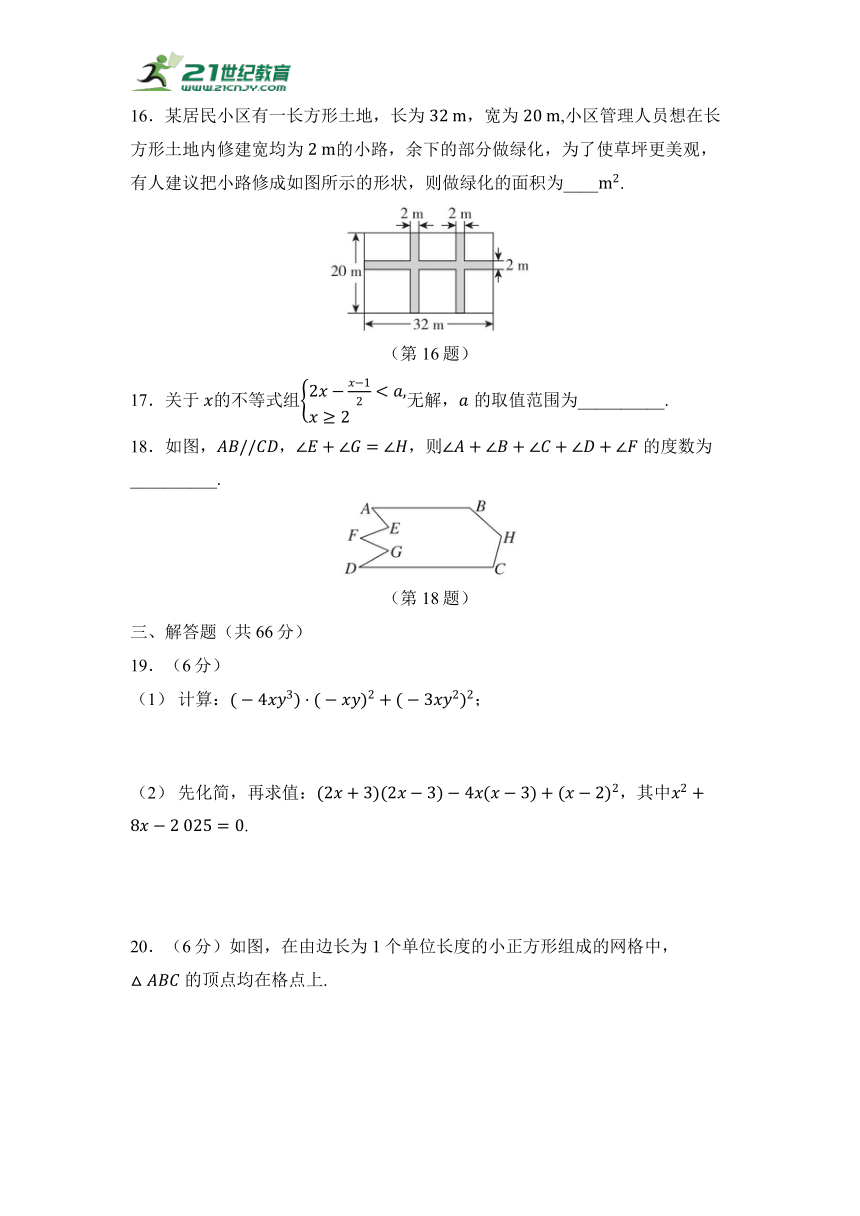
16.某居民小区有一长方形土地,长为,宽为,小区管理人员想在长方形土地内修建宽均为 的小路,余下的部分做绿化,为了使草坪更美观,有人建议把小路修成如图所示的形状,则做绿化的面积为____.
(第16题)
17.关于 的不等式组 无解,的取值范围为__________.
18.如图,,,则的度数为__________.
(第18题)
三、解答题(共66分)
19.(6分)
(1) 计算:;
(2) 先化简,再求值:,其中.
20.(6分)如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均在格点上.
(1) 先将向右平移9个单位长度,再向下平移4个单位长度,在网格中画出平移后的;
(2) 以点为中心把顺时针旋转 ,在网格中画出旋转后的;
(3) 以点所在的竖直网格线为对称轴,在网格中画出的对称图形.
21.(8分)已知关于,的方程组的解满足.
(1) 求的取值范围.
(2) 在(1)的条件下,是否存在整数,使不等式的解集为?若存在,求的值;若不存在,说明理由.
22.(8分)如图,在长方形纸片中,点在边上,将长方形纸片沿折叠后,点的对应点为点,交于点.
(1) 判断和的大小关系,并说明理由;
(2) 连接,若平分, ,求的度数.
23.(9分)全球工业互联网大会永久会址落户沈阳.为了让学生了解工业互联网相关知识,某校准备开展“工业互联网”主题活动,聘请专家为学生做五个领域的专题报告:A.数字孪生;B.人工智能;C.应用;D.工业机器人;.区块链.为了解学生的意向,在参加本次活动的学生中随机抽取部分学生下发如图所示的调查问卷,所有问卷全部收回且有效.
“工业互联网”主题活动学生意向调查问卷 请在下列选项中选择您的意向,并在其后的“”内打“√”(每名同学必选且只能选择其中一项),非常感谢您的合作. A.数字孪生 B.人工智能 C.应用 D.工业机器人 E.区块链
根据调查数据绘制成两幅不完整的统计图如图所示.
请根据统计图提供的信息,解答下列问题:
(1) 求本次调查所抽取的学生人数,并补全条形统计图;
(2) 扇形统计图中“B”对应扇形的圆心角的度数为________;
(3) 学校有600名学生参加本次活动,地点安排在两个多功能厅,每场报告时间为.由下面的活动日程表可知,A和C两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下,请你合理安排B,D,三场报告,补全活动日程表(写出一种方案即可),并说明理由.
“工业互联网”主题活动日程表
地点 时间 1号多功能厅(200座) 2号多功能厅(100座)
______ A
C ______
______ 设备检修暂停使用
24.(9分)先观察下列等式,再解答问题:
;
;
.
(1) 请你根据以上三个等式,猜想__________;
(2) 请你按照以上各等式反映的规律,写出用含的式子表示的等式:________________________________________________________________(为正整数);
(3) 计算的值.
25.(10分)“天青色等烟雨”形容的就是青花瓷中最上等的天青色,古时只能在下雨天烧制,不同釉色的瓷器价格也是大不相同.下表是某瓷器专卖店近两个月两款瓷器的销售情况:
釉色瓷器销售数量 釉色瓷器销售数量 总售价
第1个月 7套 6套 6 530元
第2个月 9套 5套 6 550元
(1) 求釉色,两款瓷器每套的售价;
(2) 若釉色瓷器的进价为300元,釉色瓷器的进价为600元,现专卖店计划用不超过8 500元购进釉色,两款瓷器一共20套,且釉色瓷器的数量不少于釉色瓷器数量的一半,请你帮忙计算有哪几种进货方案;(瓷器数量为整数)
(3) 在(2)的条件及进货方案下,求该专卖店卖出这些瓷器的最大利润.
26.(10分)已知,过内一点作交于点,作交于点.
(1) 如图①,试说明:;
(2) 如图②,射线、射线分别平分和,试说明:;
(3) 如图③,在(2)的条件下,点,在线段上,连接,,,与交于点,反向延长交于点,如果,平分, ,求的度数.
参考答案
一、选择题(每题3分,共30分)
1.A
2.C
3.D
4.C
5.B
6.B
7.D
8.B
9.C
10.C
【解析】因为,
所以,故①正确;
过点作,如图,所以.
因为,
所以,
所以,
所以,
即.
因为,,
所以,
所以,故②正确;
设,,则,,所以,.
由②知.
因为,所以 .
所以.
因为 ,所以,
所以 ,无法判断是否为 ,故③错误;
,
故④正确.
综上所述,正确的结论为①②④.故选.
二、填空题(每题3分,共24分)
11.
12.
13.D
14.60
15.38或178
【解析】设第个限速标志牌和第个摄像头到入口的距离相等.
依题意得,
整理得.
又因为,所以.
又因为,均为正整数,所以,或,.
,,
所以距离入口或处刚好同时设置有限速标志牌和摄像头.
16.504
17.
18.
【解析】如图所示,延长,交于点,
易得, .
又易知,
所以,
即.
又因为,
所以 .
三、解答题(共66分)
19.(1) 【解】原式.
(2) 原式.
因为,
所以,
所以原式.
20.(1) 【解】如图所示.
(2) 如图所示.
(3) 如图所示.
21.(1) 【解】
,得,则.
,得,则,
所以原方程组的解为
所以.
因为,所以,
解得,即的取值范围是.
(2) 存在.
因为不等式的解集为,
所以,解得.
又因为,
所以,
所以整数的值为.
22.(1) 【解】.理由如下:
由折叠知,.
因为四边形是长方形,
所以,
所以,
所以.
(2) 因为平分,
所以.
因为,
所以 ,
所以 ,
所以 .
又因为,
所以 .
23.(1) 【解】本次调查所抽取的学生人数为.
选择“D”的人数为.
补全条形统计图如下.
(2)
(3) D; B; ; 选择“B”的人数为,
选择“D”的人数为,
选择“”的人数为.
(答案不唯一)
24.(1)
(2) 【解】
(3) 因为;
;
;
…;
;
所以.
25.(1) 【解】设釉色瓷器每套的售价为元,釉色瓷器每套的售价为元.
由题意得解得
答:釉色瓷器每套的售价为350元,釉色瓷器每套的售价为680元.
(2) 设购进釉色瓷器套,则购进釉色瓷器套.
由题意得
解得.
因为为整数,所以的值为12或13.
当时,;当时,.
所以有两种进货方案:
①购进釉色瓷器12套,釉色瓷器8套;
②购进釉色瓷器13套,釉色瓷器7套.
(3) 按方案①进货时,利润为(元);
按方案②进货时,利润为(元).
因为1 210元元,
所以该专卖店卖出这些瓷器的最大利润是1 240元.
26.(1) 【解】因为,,
所以,,
所以.
(2) 过点作平分,如图①所示,
则.
因为射线,射线分别平分和,
所以,.
因为,
所以,
所以,,
所以.
(3) 因为平分,所以.
设,则,.因为,所以.
因为,所以.
所以 ,
所以.
因为 ,
所以.
过点作,过点作,如图②所示,所以 ,.所以.
因为,
所以 ,
所以 .
因为,所以 ,,
所以.
所以 .
一、选择题(每题3分,共30分)
1.浪费不以量小而为之,节约不以微小而不为.下列倡导节约能耗的图标中,文字上方的部分是轴对称图形的是( )
A. B.
C. D.
2.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
3.若与是同一个数的两个不相等的平方根,则这个数是( )
A.3 B. C.16 D.9
4.如图,在边长为9的正方形中放置两个长和宽分别为,的长方形,若长方形的周长为24,面积为,则图中阴影部分的面积为( )
(第4题)
A.18.5 B.21.5 C.27.5 D.35.5
5.已知关于 的不等式 有且只有1个负整数解,则 的取值范围是( )
A. B.
C. D.
6.如图,在锐角三角形 中,,的面积为10,平分,若,分别是,上的动点,则 的最小值为( )
(第6题)
A.4 B.5 C.4.5 D.6
7.如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , ,则 的度数为( )
(第7题)
A. B. C. D.
8.若,则 的值为( )
A.3 B. C. D.
9.已知 是25的平方根,是 的小数部分,则 的值是( )
A.3 B. C.3或 D.
10.如图,与交于点,点在直线上,,,,下列四个结论:
;;
; .
其中正确的是( )
(第10题)
A.①②③ B.②④ C.①②④ D.①④
二、填空题(每题3分,共24分)
11.若是完全平方式,则的值是________.
12.若关于的多项式的乘积化简后不含项,则______.
13.如图,在数轴上标有字母的各点中,与实数对应的可能是点______.
(第13题)
14.如图,点是正六边形的中心,分别以各边为直径向正六边形的外部作半圆,组成了一幅美丽的图案,这个图案绕点至少旋转__ 后能与原来的图案互相重合.
(第14题)
15.如图,某段高速公路全长,交警部门在该段高速公路距离入口处设立了限速标志牌,并在以后每隔处设置一块限速标志牌,此外交警部门还在距离入口处设置了摄像头,并在以后每隔处都设置一个摄像头.则距离入口________处刚好同时设置有限速标志牌和摄像头.
(第15题)
16.某居民小区有一长方形土地,长为,宽为,小区管理人员想在长方形土地内修建宽均为 的小路,余下的部分做绿化,为了使草坪更美观,有人建议把小路修成如图所示的形状,则做绿化的面积为____.
(第16题)
17.关于 的不等式组 无解,的取值范围为__________.
18.如图,,,则的度数为__________.
(第18题)
三、解答题(共66分)
19.(6分)
(1) 计算:;
(2) 先化简,再求值:,其中.
20.(6分)如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均在格点上.
(1) 先将向右平移9个单位长度,再向下平移4个单位长度,在网格中画出平移后的;
(2) 以点为中心把顺时针旋转 ,在网格中画出旋转后的;
(3) 以点所在的竖直网格线为对称轴,在网格中画出的对称图形.
21.(8分)已知关于,的方程组的解满足.
(1) 求的取值范围.
(2) 在(1)的条件下,是否存在整数,使不等式的解集为?若存在,求的值;若不存在,说明理由.
22.(8分)如图,在长方形纸片中,点在边上,将长方形纸片沿折叠后,点的对应点为点,交于点.
(1) 判断和的大小关系,并说明理由;
(2) 连接,若平分, ,求的度数.
23.(9分)全球工业互联网大会永久会址落户沈阳.为了让学生了解工业互联网相关知识,某校准备开展“工业互联网”主题活动,聘请专家为学生做五个领域的专题报告:A.数字孪生;B.人工智能;C.应用;D.工业机器人;.区块链.为了解学生的意向,在参加本次活动的学生中随机抽取部分学生下发如图所示的调查问卷,所有问卷全部收回且有效.
“工业互联网”主题活动学生意向调查问卷 请在下列选项中选择您的意向,并在其后的“”内打“√”(每名同学必选且只能选择其中一项),非常感谢您的合作. A.数字孪生 B.人工智能 C.应用 D.工业机器人 E.区块链
根据调查数据绘制成两幅不完整的统计图如图所示.
请根据统计图提供的信息,解答下列问题:
(1) 求本次调查所抽取的学生人数,并补全条形统计图;
(2) 扇形统计图中“B”对应扇形的圆心角的度数为________;
(3) 学校有600名学生参加本次活动,地点安排在两个多功能厅,每场报告时间为.由下面的活动日程表可知,A和C两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下,请你合理安排B,D,三场报告,补全活动日程表(写出一种方案即可),并说明理由.
“工业互联网”主题活动日程表
地点 时间 1号多功能厅(200座) 2号多功能厅(100座)
______ A
C ______
______ 设备检修暂停使用
24.(9分)先观察下列等式,再解答问题:
;
;
.
(1) 请你根据以上三个等式,猜想__________;
(2) 请你按照以上各等式反映的规律,写出用含的式子表示的等式:________________________________________________________________(为正整数);
(3) 计算的值.
25.(10分)“天青色等烟雨”形容的就是青花瓷中最上等的天青色,古时只能在下雨天烧制,不同釉色的瓷器价格也是大不相同.下表是某瓷器专卖店近两个月两款瓷器的销售情况:
釉色瓷器销售数量 釉色瓷器销售数量 总售价
第1个月 7套 6套 6 530元
第2个月 9套 5套 6 550元
(1) 求釉色,两款瓷器每套的售价;
(2) 若釉色瓷器的进价为300元,釉色瓷器的进价为600元,现专卖店计划用不超过8 500元购进釉色,两款瓷器一共20套,且釉色瓷器的数量不少于釉色瓷器数量的一半,请你帮忙计算有哪几种进货方案;(瓷器数量为整数)
(3) 在(2)的条件及进货方案下,求该专卖店卖出这些瓷器的最大利润.
26.(10分)已知,过内一点作交于点,作交于点.
(1) 如图①,试说明:;
(2) 如图②,射线、射线分别平分和,试说明:;
(3) 如图③,在(2)的条件下,点,在线段上,连接,,,与交于点,反向延长交于点,如果,平分, ,求的度数.
参考答案
一、选择题(每题3分,共30分)
1.A
2.C
3.D
4.C
5.B
6.B
7.D
8.B
9.C
10.C
【解析】因为,
所以,故①正确;
过点作,如图,所以.
因为,
所以,
所以,
所以,
即.
因为,,
所以,
所以,故②正确;
设,,则,,所以,.
由②知.
因为,所以 .
所以.
因为 ,所以,
所以 ,无法判断是否为 ,故③错误;
,
故④正确.
综上所述,正确的结论为①②④.故选.
二、填空题(每题3分,共24分)
11.
12.
13.D
14.60
15.38或178
【解析】设第个限速标志牌和第个摄像头到入口的距离相等.
依题意得,
整理得.
又因为,所以.
又因为,均为正整数,所以,或,.
,,
所以距离入口或处刚好同时设置有限速标志牌和摄像头.
16.504
17.
18.
【解析】如图所示,延长,交于点,
易得, .
又易知,
所以,
即.
又因为,
所以 .
三、解答题(共66分)
19.(1) 【解】原式.
(2) 原式.
因为,
所以,
所以原式.
20.(1) 【解】如图所示.
(2) 如图所示.
(3) 如图所示.
21.(1) 【解】
,得,则.
,得,则,
所以原方程组的解为
所以.
因为,所以,
解得,即的取值范围是.
(2) 存在.
因为不等式的解集为,
所以,解得.
又因为,
所以,
所以整数的值为.
22.(1) 【解】.理由如下:
由折叠知,.
因为四边形是长方形,
所以,
所以,
所以.
(2) 因为平分,
所以.
因为,
所以 ,
所以 ,
所以 .
又因为,
所以 .
23.(1) 【解】本次调查所抽取的学生人数为.
选择“D”的人数为.
补全条形统计图如下.
(2)
(3) D; B; ; 选择“B”的人数为,
选择“D”的人数为,
选择“”的人数为.
(答案不唯一)
24.(1)
(2) 【解】
(3) 因为;
;
;
…;
;
所以.
25.(1) 【解】设釉色瓷器每套的售价为元,釉色瓷器每套的售价为元.
由题意得解得
答:釉色瓷器每套的售价为350元,釉色瓷器每套的售价为680元.
(2) 设购进釉色瓷器套,则购进釉色瓷器套.
由题意得
解得.
因为为整数,所以的值为12或13.
当时,;当时,.
所以有两种进货方案:
①购进釉色瓷器12套,釉色瓷器8套;
②购进釉色瓷器13套,釉色瓷器7套.
(3) 按方案①进货时,利润为(元);
按方案②进货时,利润为(元).
因为1 210元元,
所以该专卖店卖出这些瓷器的最大利润是1 240元.
26.(1) 【解】因为,,
所以,,
所以.
(2) 过点作平分,如图①所示,
则.
因为射线,射线分别平分和,
所以,.
因为,
所以,
所以,,
所以.
(3) 因为平分,所以.
设,则,.因为,所以.
因为,所以.
所以 ,
所以.
因为 ,
所以.
过点作,过点作,如图②所示,所以 ,.所以.
因为,
所以 ,
所以 .
因为,所以 ,,
所以.
所以 .
同课章节目录
