2025新湘教版七年级数学下册期中测试卷(含答案)
文档属性
| 名称 | 2025新湘教版七年级数学下册期中测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 224.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 09:36:10 | ||
图片预览




文档简介
2025新湘教版七年级数学下册期中测试卷
时间:120分钟 满分:120分钟
一、单选题(每题3分,共30分)
1.已知,则的值为( )
A.6 B.7 C.8 D.9
2.在,,,,,中,无理数有( )
A.3个 B.4个 C.5个 D.6个
3.下列说法中正确的是( )
A.64的立方根是 B.没有立方根
C.是64的平方根 D.的平方根是
4.已知关于的多项式与的乘积的展开式中不含的二次项,则的值为( )
A. B. C. D.3
5.的个位上的数字是( )
A.3 B.9 C.7 D.1
6.如图,在边长为的正方形中挖掉一个边长为的小正方形,把剩下的部分剪拼成一个长方形,通过计算两处图形(阴影部分)的面积,验证了一个等式,这个等式是( )
A. B.
C. D.
7.在第55个“世界地球日”来临之际,为贯彻落实习近平总书记在党的二十大报告中提出的推动绿色发展、促进人与自然和谐共生,牢固树立和践行绿水青山就是金山银山的理念,某省生态文明建设促进会计划组织大学生进行环保知识竞赛.已知竞赛试题共有30道,每道题答对得5分,答错或不答都扣2分.小陈得分要超过100分,他答对的题数至少是( )
A.21 B.22 C.23 D.24
8.已知关于的不等式组的解集是,则的值等于( )
A. B. C. D.
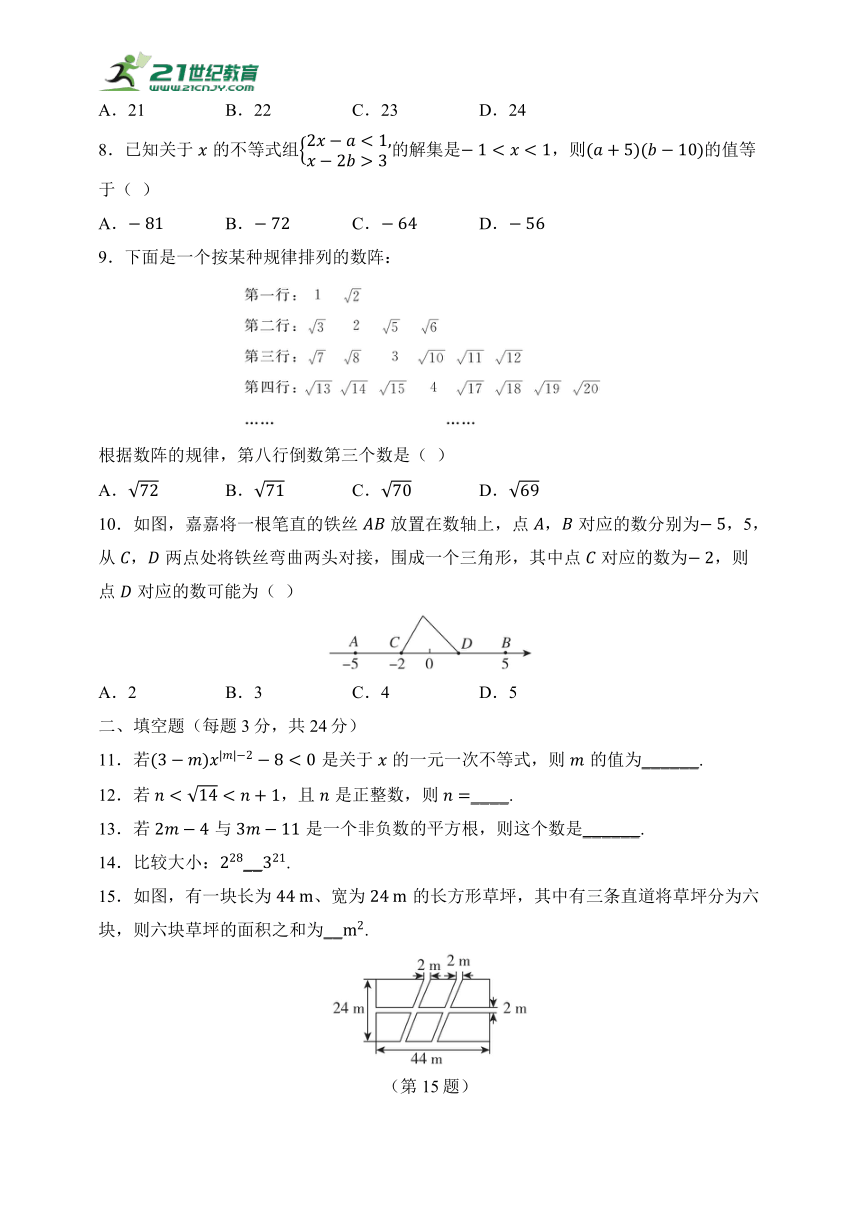
9.下面是一个按某种规律排列的数阵:
根据数阵的规律,第八行倒数第三个数是( )
A. B. C. D.
10.如图,嘉嘉将一根笔直的铁丝放置在数轴上,点,对应的数分别为,5,从,两点处将铁丝弯曲两头对接,围成一个三角形,其中点对应的数为,则点对应的数可能为( )
A.2 B.3 C.4 D.5
二、填空题(每题3分,共24分)
11.若是关于的一元一次不等式,则的值为_ _ _ _ _ _ .
12.若,且是正整数,则_ _ _ _ .
13.若与是一个非负数的平方根,则这个数是_ _ _ _ _ _ .
14.比较大小:_ _ .
15.如图,有一块长为、宽为的长方形草坪,其中有三条直道将草坪分为六块,则六块草坪的面积之和为_ _ .
(第15题)
16.如图,将面积为5的正方形放在数轴上,以表示的点为圆心,以正方形的边长为半径作圆,交数轴于,两点,则点,表示的数分别为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
(第16题)
17.若,则_ _ .
18.已知有理数,,满足,那么的值为_ _ _ _ .
三、解答题(共66分)
19.(8分)计算:
(1) ; (2) ;
(3) ;
(4) 5.
20.(6分)
(1) 解不等式,并把解集在数轴上表示出来;
(2) 解不等式组并把它的解集表示在数轴上.
21.(6分)先化简,再求值:当,时,求代数式的值.
22.(6分)已知的立方根是3,的算术平方根是4,是的整数部分.
(1) 求,,的值;
(2) 求的平方根.
23.(8分)对一个的值按如图所示的程序进行操作,规定:程序运行从“输入一个的值”到“判断结果是否大于190”为1次操作.
(1) 当输入时,要操作_ _ _ _ 次才停止;
(2) 如果操作只进行1次就停止,求的取值范围;
(3) 如果操作恰好进行3次才停止,求的取值范围.
24.(10分)高尔基说:“书籍是人类进步的阶梯.”为提高学生的阅读水平,某中学购买了“科普类”和“文学类”两种图书,其中“科普类”图书的单价比“文学类”图书的单价多4元,购买30本“科普类”图书和40本“文学类”图书共花费1 240元.
(1) 求这两种图书的单价分别是多少元;
(2) 学校决定再次购买这两种图书共100本,这次购买的总费用超过1 790元但不超过1 800元,则学校有哪几种购买方案?
25.(10分)根据以下素材,探索完成任务1和任务2:
主题:奶茶销售方案制定问题
年轻人喜欢喝奶茶,入夏之际某知名奶茶品牌店推出两款爆款水果茶“满杯杨梅”和“芝士杨梅”.
素材1 两款奶茶配料表如下:
芝士杨梅 19元/杯 配料
芝士/杯
茉莉清茶/杯
杨梅肉
多肉
满杯杨梅 17元/杯 配料
茉莉清茶/杯
杨梅肉
多肉
素材2 9月2日当天销售“芝士杨梅”共获利润400元,“满杯杨梅”共获利润480元,其中每杯“芝士杨梅”的利润是每杯“满杯杨梅”的 倍,“满杯杨梅”比“芝士杨梅”多卖20杯.
素材3 由于芝士保质期将至,为了去库存,9月3日决定对“芝士杨梅”每杯降价4元促销,并要求当天的芝士消耗量不少于,配制的 茉莉清茶全部用于制作“芝士杨梅”和“满杯杨梅”.
问题解决
任务1 确定奶茶的利润 每杯“芝士杨梅”和“满杯杨梅”的利润分别是多少?
任务2 拟定最优方案 为了使9月3日这两种水果茶获利最大,需制作“芝士杨梅”和“满杯杨梅”共多少杯?
26.(12分)阅读下列材料,解决相应问题:
已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原来两个两位数均不同的新数,若原来两个两位数的乘积与交换位置后两个新两位数的乘积相等,则称交换位置前后的两个两位数都为“倒同数对”.
例如:,所以23和96与32和69都是“倒同数对”.
(1) 请判断43和68是否是“倒同数对”,并说明理由;
(2) 为探究“倒同数对”的本质,可设“倒同数对”中一个数的十位数字为,个位数字为,且;另一个数的十位数字为,个位数字为,且,请探究,,,的数量关系,并说明理由;
(3) 若有一个两位数,十位数字为,个位数字为,另一个两位数,十位数字为,个位数字为,且这两个数为“倒同数对”,则的值为_ _ _ _ .
参考答案
一、单选题(每题3分,共30分)
1.C 2.A 3.C 4.C 5.C 6.A 7.C 8.B 9.C 10.A
二、填空题(每题3分,共24分)
11.
12.3
13.100或4
14.
15.880
16.,
17.2025
[解析]方法点睛:设,,则,,再由进行求解即可.
18.6
三、解答题(共66分)
19.(1) 解:原式.
(2) 原式.
(3) 原式.
(4) 原式.
20.(1) 解:,
去分母,得,
去括号,得,
移项,得,
合并同类项,得,系数化为1,得.
所以不等式的解集为.
在数轴上表示如图.
(2) 解不等式①,得,解不等式②,得.
所以不等式组的解集为.
在数轴上表示如图.
21.解:
.
当,时,
原式.
22.(1) 解:因为的立方根是3,所以,解得,因为的算术平方根是4,所以,又因为,所以,因为是的整数部分,,所以,所以,综上所述,,,.
(2) 把,,代入,得,所以的平方根是.
23.(1) 5
(2) 解:第1次操作的结果为,
若操作只进行1次就停止,则,
解得.故的取值范围是.
(3) 第1次操作的结果为,没有停止,则,解得;
第2次操作的结果为,没有停止,则,解得;
第3次操作的结果为,停止,则,解得.
综上所述,的取值范围是.
24.(1) 解:设“科普类”图书的单价为元,则“文学类”图书的单价为元,由题意得,
解得,则.
答:“科普类”图书的单价为20元,“文学类”图书的单价为16元.
(2) 设再次购买“文学类”图书本,则再次购买“科普类”图书本,
依题意得
解得.
因为是正整数,所以,51,52.
所以学校有3种购买方案:再次购买50本“文学类”图书,50本“科普类”图书;再次购买51本“文学类”图书,49本“科普类”图书;再次购买52本“文学类”图书,48本“科普类”图书.
25.解:任务1:设每杯“满杯杨梅”的利润是元,则每杯“芝士杨梅”的利润为元,9月2日当天销售“芝士杨梅”杯,则销售“满杯杨梅”杯,由题意可得由可得,把代入,可得,所以,.
所以每杯“满杯杨梅”的利润是8元,每杯“芝士杨梅”的利润为10元.
任务2:设9月3日制作“芝士杨梅”和“满杯杨梅”分别为杯和杯,总获利为元,
由题意可得
由可得,
所以解得,
又因为和都是正整数,所以必须是5的倍数,所以或.当时,,;当时,,,因为,所以为了使9月3日这两种水果茶获利最大,需制作“芝士杨梅”35杯,“满杯杨梅”7杯,共(杯).
26.(1) 解:43和68是“倒同数对”,理由如下:
因为,,
所以,
所以43和68是“倒同数对”.
(2) ,理由如下:
由题意可得,
,
,
即.
(3) 1
[解析]由题意得,
整理得,
,
,解得.
时间:120分钟 满分:120分钟
一、单选题(每题3分,共30分)
1.已知,则的值为( )
A.6 B.7 C.8 D.9
2.在,,,,,中,无理数有( )
A.3个 B.4个 C.5个 D.6个
3.下列说法中正确的是( )
A.64的立方根是 B.没有立方根
C.是64的平方根 D.的平方根是
4.已知关于的多项式与的乘积的展开式中不含的二次项,则的值为( )
A. B. C. D.3
5.的个位上的数字是( )
A.3 B.9 C.7 D.1
6.如图,在边长为的正方形中挖掉一个边长为的小正方形,把剩下的部分剪拼成一个长方形,通过计算两处图形(阴影部分)的面积,验证了一个等式,这个等式是( )
A. B.
C. D.
7.在第55个“世界地球日”来临之际,为贯彻落实习近平总书记在党的二十大报告中提出的推动绿色发展、促进人与自然和谐共生,牢固树立和践行绿水青山就是金山银山的理念,某省生态文明建设促进会计划组织大学生进行环保知识竞赛.已知竞赛试题共有30道,每道题答对得5分,答错或不答都扣2分.小陈得分要超过100分,他答对的题数至少是( )
A.21 B.22 C.23 D.24
8.已知关于的不等式组的解集是,则的值等于( )
A. B. C. D.
9.下面是一个按某种规律排列的数阵:
根据数阵的规律,第八行倒数第三个数是( )
A. B. C. D.
10.如图,嘉嘉将一根笔直的铁丝放置在数轴上,点,对应的数分别为,5,从,两点处将铁丝弯曲两头对接,围成一个三角形,其中点对应的数为,则点对应的数可能为( )
A.2 B.3 C.4 D.5
二、填空题(每题3分,共24分)
11.若是关于的一元一次不等式,则的值为_ _ _ _ _ _ .
12.若,且是正整数,则_ _ _ _ .
13.若与是一个非负数的平方根,则这个数是_ _ _ _ _ _ .
14.比较大小:_ _ .
15.如图,有一块长为、宽为的长方形草坪,其中有三条直道将草坪分为六块,则六块草坪的面积之和为_ _ .
(第15题)
16.如图,将面积为5的正方形放在数轴上,以表示的点为圆心,以正方形的边长为半径作圆,交数轴于,两点,则点,表示的数分别为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
(第16题)
17.若,则_ _ .
18.已知有理数,,满足,那么的值为_ _ _ _ .
三、解答题(共66分)
19.(8分)计算:
(1) ; (2) ;
(3) ;
(4) 5.
20.(6分)
(1) 解不等式,并把解集在数轴上表示出来;
(2) 解不等式组并把它的解集表示在数轴上.
21.(6分)先化简,再求值:当,时,求代数式的值.
22.(6分)已知的立方根是3,的算术平方根是4,是的整数部分.
(1) 求,,的值;
(2) 求的平方根.
23.(8分)对一个的值按如图所示的程序进行操作,规定:程序运行从“输入一个的值”到“判断结果是否大于190”为1次操作.
(1) 当输入时,要操作_ _ _ _ 次才停止;
(2) 如果操作只进行1次就停止,求的取值范围;
(3) 如果操作恰好进行3次才停止,求的取值范围.
24.(10分)高尔基说:“书籍是人类进步的阶梯.”为提高学生的阅读水平,某中学购买了“科普类”和“文学类”两种图书,其中“科普类”图书的单价比“文学类”图书的单价多4元,购买30本“科普类”图书和40本“文学类”图书共花费1 240元.
(1) 求这两种图书的单价分别是多少元;
(2) 学校决定再次购买这两种图书共100本,这次购买的总费用超过1 790元但不超过1 800元,则学校有哪几种购买方案?
25.(10分)根据以下素材,探索完成任务1和任务2:
主题:奶茶销售方案制定问题
年轻人喜欢喝奶茶,入夏之际某知名奶茶品牌店推出两款爆款水果茶“满杯杨梅”和“芝士杨梅”.
素材1 两款奶茶配料表如下:
芝士杨梅 19元/杯 配料
芝士/杯
茉莉清茶/杯
杨梅肉
多肉
满杯杨梅 17元/杯 配料
茉莉清茶/杯
杨梅肉
多肉
素材2 9月2日当天销售“芝士杨梅”共获利润400元,“满杯杨梅”共获利润480元,其中每杯“芝士杨梅”的利润是每杯“满杯杨梅”的 倍,“满杯杨梅”比“芝士杨梅”多卖20杯.
素材3 由于芝士保质期将至,为了去库存,9月3日决定对“芝士杨梅”每杯降价4元促销,并要求当天的芝士消耗量不少于,配制的 茉莉清茶全部用于制作“芝士杨梅”和“满杯杨梅”.
问题解决
任务1 确定奶茶的利润 每杯“芝士杨梅”和“满杯杨梅”的利润分别是多少?
任务2 拟定最优方案 为了使9月3日这两种水果茶获利最大,需制作“芝士杨梅”和“满杯杨梅”共多少杯?
26.(12分)阅读下列材料,解决相应问题:
已知两个两位数,将它们各自的十位数字和个位数字交换位置后,得到两个与原来两个两位数均不同的新数,若原来两个两位数的乘积与交换位置后两个新两位数的乘积相等,则称交换位置前后的两个两位数都为“倒同数对”.
例如:,所以23和96与32和69都是“倒同数对”.
(1) 请判断43和68是否是“倒同数对”,并说明理由;
(2) 为探究“倒同数对”的本质,可设“倒同数对”中一个数的十位数字为,个位数字为,且;另一个数的十位数字为,个位数字为,且,请探究,,,的数量关系,并说明理由;
(3) 若有一个两位数,十位数字为,个位数字为,另一个两位数,十位数字为,个位数字为,且这两个数为“倒同数对”,则的值为_ _ _ _ .
参考答案
一、单选题(每题3分,共30分)
1.C 2.A 3.C 4.C 5.C 6.A 7.C 8.B 9.C 10.A
二、填空题(每题3分,共24分)
11.
12.3
13.100或4
14.
15.880
16.,
17.2025
[解析]方法点睛:设,,则,,再由进行求解即可.
18.6
三、解答题(共66分)
19.(1) 解:原式.
(2) 原式.
(3) 原式.
(4) 原式.
20.(1) 解:,
去分母,得,
去括号,得,
移项,得,
合并同类项,得,系数化为1,得.
所以不等式的解集为.
在数轴上表示如图.
(2) 解不等式①,得,解不等式②,得.
所以不等式组的解集为.
在数轴上表示如图.
21.解:
.
当,时,
原式.
22.(1) 解:因为的立方根是3,所以,解得,因为的算术平方根是4,所以,又因为,所以,因为是的整数部分,,所以,所以,综上所述,,,.
(2) 把,,代入,得,所以的平方根是.
23.(1) 5
(2) 解:第1次操作的结果为,
若操作只进行1次就停止,则,
解得.故的取值范围是.
(3) 第1次操作的结果为,没有停止,则,解得;
第2次操作的结果为,没有停止,则,解得;
第3次操作的结果为,停止,则,解得.
综上所述,的取值范围是.
24.(1) 解:设“科普类”图书的单价为元,则“文学类”图书的单价为元,由题意得,
解得,则.
答:“科普类”图书的单价为20元,“文学类”图书的单价为16元.
(2) 设再次购买“文学类”图书本,则再次购买“科普类”图书本,
依题意得
解得.
因为是正整数,所以,51,52.
所以学校有3种购买方案:再次购买50本“文学类”图书,50本“科普类”图书;再次购买51本“文学类”图书,49本“科普类”图书;再次购买52本“文学类”图书,48本“科普类”图书.
25.解:任务1:设每杯“满杯杨梅”的利润是元,则每杯“芝士杨梅”的利润为元,9月2日当天销售“芝士杨梅”杯,则销售“满杯杨梅”杯,由题意可得由可得,把代入,可得,所以,.
所以每杯“满杯杨梅”的利润是8元,每杯“芝士杨梅”的利润为10元.
任务2:设9月3日制作“芝士杨梅”和“满杯杨梅”分别为杯和杯,总获利为元,
由题意可得
由可得,
所以解得,
又因为和都是正整数,所以必须是5的倍数,所以或.当时,,;当时,,,因为,所以为了使9月3日这两种水果茶获利最大,需制作“芝士杨梅”35杯,“满杯杨梅”7杯,共(杯).
26.(1) 解:43和68是“倒同数对”,理由如下:
因为,,
所以,
所以43和68是“倒同数对”.
(2) ,理由如下:
由题意可得,
,
,
即.
(3) 1
[解析]由题意得,
整理得,
,
,解得.
同课章节目录
