【核心考点集训】第五单元《三角形》课件(共17张PPT)--人教版四年级下册数学
文档属性
| 名称 | 【核心考点集训】第五单元《三角形》课件(共17张PPT)--人教版四年级下册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 08:53:56 | ||
图片预览






文档简介
(共17张PPT)
人教版 数学 四年级 下册
三角形
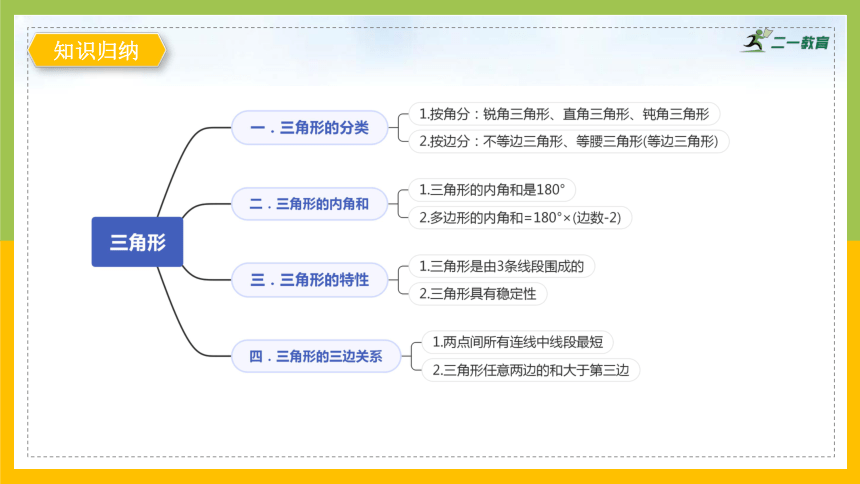
知识归纳
模块一:知识点复习
知识点一:三角形的特性
知识梳理
1.由3条线段围成的图形(每相邻两条线段的端点相连)叫作三角形。
2.三角形有3条边、3个角和3个顶点。
3.从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高,这条对边叫作三角形的底,画高时要用虚线表示,画完后标上直角符号。
4.三角形具有稳定性。
5.两点间所有连线中线段最短,这条线段的长度叫作两点间的距离。
6.三角形任意两边的和大于第三边。
7.判断3条线段能否围成三角形,只要把较短的两条线段相加的和与最长线段比较,大于最长的线段就能围成三角形,反之则不能。
知识点二:三角形的分类
知识梳理
1.三角形按角分类:锐角三角形、直角三角形和钝角三角形。
2.三个角都是锐角的三角形叫作锐角三角形,有一个角是直角的三角形叫作直角三角形,有一个角是钝角的三角形叫作钝角三角形。
3.等腰三角形:两条边相等的三角形叫作等腰三角形。在等腰三角形里,相等的两条边叫作腰,另一条边叫作底,两腰的夹角叫作顶角,底和腰的两个夹角叫作底角。等腰三角形的两腰相等,两个底角也相等。
4.等边三角形:三条边都相等的三角形叫作等边三角形,又叫作正三角形。等边三角形也是等腰三角形,但等腰三角形不一定是等边三角形。等边三角形中的每个角都是60°。
知识点三:三角形的内角和
知识梳理
1.三角形的每两条边所形成的角叫作三角形的内角,每个三角形都有3个内角。三角形的内角和等于180°,与三角形的大小、形状无关。
2.在三角形的3个内角中,已知两个角的度数,求第三个角的度数,用内角和180°连续减去已知的两个角的度数或减去这两个角的度数和。
3.四边形的内角和是360°。
4.多边形的内角和=180°×(边数-2)。
模块二:例题讲解
【典例1】用组合规律解决摆三角形问题
分析:5根小棒中选择3根摆三角形,3根小棒的长度一定要符合“三角形任意两边的和大于第三边”这一规律。
①当最长边是7cm时,所有的组合情况有(7、6、5),(7、6、4),(7、6、3),(7、5、4),(7、5、3),共有5种情况。
②当最长边是6cm时,所有的组合情况有(6、5、4),(6、5、3),(6、4、3),共有3种情况。
③当最长边是5cm时,所有的组合情况有(5、4、3),只有1种情况。
解答:5+3+1=9(种) 一共有9情况。
从5根长度分别是3cm、4cm、5cm、6cm、7cm的小棒中选择3根摆三角形,你能摆出几种不同的三角形
【典例2】用假设法解决等腰三角形的边长问题
分析:解决关于等腰三角形的边长问题时,要注意两点:
①等腰三角形两腰的长度相等; ②三角形任意两边的和大于第三边。
由题可知,画框的第三条边可能是64cm,也可能是28cm。
欣欣想做一个等腰三角形的画框。已知画框的两条边分别为64 cm和28cm,第三条边长( )cm。
假设第三条边长64cm
64+28>64
能围成三角形
假设第三条边长28cm
64+28<64
不能围成三角形
第三条边长64cm
64
【典例3】用分类讨论法求等腰三角形内角的度数
分析:在等腰三角形中,当已知角小于90°时,这个角可能是顶角,也可能是底角;当已知角大于或等于90°时,这个角只能是顶角。本题可分情况讨论如下。
顶角是80°时:
每个底角的度数=(180°-顶角的度数)÷2=(180°-80°)÷2=50°
底角是80°时:
顶角的度数:=180°-底角的度数×2=180°-80°×2=20°
一个等腰三角形,其中一个角的度数是80°,求另外两个角的度数。
解答:情况一:(180°-80°)÷2=50°
情况二:180°-80°×2=20°
答:顶角是80°时,另外两个角都是50°;底角是80时,另外两个角分别是80°、20°
【典例4】用等量代换法求三角形内角的度数
分析:根据题意,假设直角三角形的三个内角分别是∠A、∠B和∠C,且∠C=90°。
三角形的内角和是180°
∠A+∠B+∠C=180°
∠C=90°
∠A+∠B=180°-90°=90°
∠B+20°+∠B=90°
∠B=(90°-20°)÷2=35°
∠A=35°+20°=55°
解答:180°-90°=90°
(90°-20°)÷2=35°
35°+20°=55°
答:两个锐角的度数分别是35°和55°。
一个直角三角形,其中一个锐角比另一个锐角大20°,求两个锐角的度数。
∠A比∠B大20°
∠A=∠B+20°
两个锐角的度数
【典例5】用观察法解决稍复杂的三角形内角度数问题
分析:通过观察可知,正方形的顶点A、B都与线段EF上的点G重合,线段DG和CG是正方形的边,即DG=CG=CD,由此可知,三角形CGD是等边三角形,所以∠1=60。
如图,在正方形ABCD中,E、F分别是线段AB、CD的中点,将正方形的∠A和∠B折起,使顶点A、B都与线段EF上的点G重合,求∠1的度数。
解答:DG=CG=CD
三角形CGD是等边三角形
∠1=180÷3=60°
答:∠1的度数是60°。
模块三:完成变式训练
1.小强家要建一座漂亮的房子,请你帮他选择3根木料做成房子的三角架,并说明你选择的理由。(提示:三角架有两边相等)
分析:在选择木料时,注意房子的三角架有两边是相等的,可以
先确定两根相等的木料,再选择第三根木料。
解答:6、6、3;6+3>6,6+6>3 能摆成三角形
6、6、5;6+5>6,6+6>5 能摆成三角形
3、3、6;3+3=6 不能摆成三角形
3、3、5;3+5>3,3+3>5 能摆成三角形
可以选(6、6、3)或(6、6、5)或(3、3、5)
理由:它们每组的三个数都满足三角形任意两边的和大于第三边,即都能拼成三角形,且有两边相等。
2.陈伯伯家有一块等腰三角形菜地,他用长是18m的篱笆恰好围了一圈。其中一条边长是4m,另外两边分别是多少?
解答:情况一:4m是腰长,那么底边长为18-4×2=10(m)
因为:4+4=8<10,不满足三角形任意两边之和大于第三边,
所以:这种情况不成立。
情况二:4m是底边长,那么腰长为(18-4)÷2=7(m)
此时7+7=14>4,7+4=11>7,满足三角形三边关系,
所以:另外两边分别是7m、7m。
3.在等腰三角形中,较大角是较小角度数的4倍。这个三角形的顶角与底角各是多少度
解答:情况一:较大角是顶角时
180°÷(4+1+1)=30°30°×4=120°
情况二;较大角是底角时
180°÷(4+4+1)=20°20°×4=80°
答:当较大角是顶角时,顶角是120°,底角是30°;当较大角是底角时,顶角是20°,底角是80°。
4.在三角形ABC中,已知∠A=30°,∠B是∠C的2倍,求∠B的度数。
解答:180°-30°=150°
150°÷(2+1)=50°
2×50°=100°
答:∠B的度数是100°。
5.如图,在一张三角形纸片ABC中,∠C=90°,将这张纸片沿线段DE剪去一个角后变成一个四边形ABED,那么图中∠1+∠2等于多少度
解答:∠A+∠B=180°-∠C=180°-90°=90°
∠1+∠2=360°-(∠A+∠B)=360°-90°=270°
答:∠1+∠2等于270°。
人教版 数学 四年级 下册
三角形
知识归纳
模块一:知识点复习
知识点一:三角形的特性
知识梳理
1.由3条线段围成的图形(每相邻两条线段的端点相连)叫作三角形。
2.三角形有3条边、3个角和3个顶点。
3.从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高,这条对边叫作三角形的底,画高时要用虚线表示,画完后标上直角符号。
4.三角形具有稳定性。
5.两点间所有连线中线段最短,这条线段的长度叫作两点间的距离。
6.三角形任意两边的和大于第三边。
7.判断3条线段能否围成三角形,只要把较短的两条线段相加的和与最长线段比较,大于最长的线段就能围成三角形,反之则不能。
知识点二:三角形的分类
知识梳理
1.三角形按角分类:锐角三角形、直角三角形和钝角三角形。
2.三个角都是锐角的三角形叫作锐角三角形,有一个角是直角的三角形叫作直角三角形,有一个角是钝角的三角形叫作钝角三角形。
3.等腰三角形:两条边相等的三角形叫作等腰三角形。在等腰三角形里,相等的两条边叫作腰,另一条边叫作底,两腰的夹角叫作顶角,底和腰的两个夹角叫作底角。等腰三角形的两腰相等,两个底角也相等。
4.等边三角形:三条边都相等的三角形叫作等边三角形,又叫作正三角形。等边三角形也是等腰三角形,但等腰三角形不一定是等边三角形。等边三角形中的每个角都是60°。
知识点三:三角形的内角和
知识梳理
1.三角形的每两条边所形成的角叫作三角形的内角,每个三角形都有3个内角。三角形的内角和等于180°,与三角形的大小、形状无关。
2.在三角形的3个内角中,已知两个角的度数,求第三个角的度数,用内角和180°连续减去已知的两个角的度数或减去这两个角的度数和。
3.四边形的内角和是360°。
4.多边形的内角和=180°×(边数-2)。
模块二:例题讲解
【典例1】用组合规律解决摆三角形问题
分析:5根小棒中选择3根摆三角形,3根小棒的长度一定要符合“三角形任意两边的和大于第三边”这一规律。
①当最长边是7cm时,所有的组合情况有(7、6、5),(7、6、4),(7、6、3),(7、5、4),(7、5、3),共有5种情况。
②当最长边是6cm时,所有的组合情况有(6、5、4),(6、5、3),(6、4、3),共有3种情况。
③当最长边是5cm时,所有的组合情况有(5、4、3),只有1种情况。
解答:5+3+1=9(种) 一共有9情况。
从5根长度分别是3cm、4cm、5cm、6cm、7cm的小棒中选择3根摆三角形,你能摆出几种不同的三角形
【典例2】用假设法解决等腰三角形的边长问题
分析:解决关于等腰三角形的边长问题时,要注意两点:
①等腰三角形两腰的长度相等; ②三角形任意两边的和大于第三边。
由题可知,画框的第三条边可能是64cm,也可能是28cm。
欣欣想做一个等腰三角形的画框。已知画框的两条边分别为64 cm和28cm,第三条边长( )cm。
假设第三条边长64cm
64+28>64
能围成三角形
假设第三条边长28cm
64+28<64
不能围成三角形
第三条边长64cm
64
【典例3】用分类讨论法求等腰三角形内角的度数
分析:在等腰三角形中,当已知角小于90°时,这个角可能是顶角,也可能是底角;当已知角大于或等于90°时,这个角只能是顶角。本题可分情况讨论如下。
顶角是80°时:
每个底角的度数=(180°-顶角的度数)÷2=(180°-80°)÷2=50°
底角是80°时:
顶角的度数:=180°-底角的度数×2=180°-80°×2=20°
一个等腰三角形,其中一个角的度数是80°,求另外两个角的度数。
解答:情况一:(180°-80°)÷2=50°
情况二:180°-80°×2=20°
答:顶角是80°时,另外两个角都是50°;底角是80时,另外两个角分别是80°、20°
【典例4】用等量代换法求三角形内角的度数
分析:根据题意,假设直角三角形的三个内角分别是∠A、∠B和∠C,且∠C=90°。
三角形的内角和是180°
∠A+∠B+∠C=180°
∠C=90°
∠A+∠B=180°-90°=90°
∠B+20°+∠B=90°
∠B=(90°-20°)÷2=35°
∠A=35°+20°=55°
解答:180°-90°=90°
(90°-20°)÷2=35°
35°+20°=55°
答:两个锐角的度数分别是35°和55°。
一个直角三角形,其中一个锐角比另一个锐角大20°,求两个锐角的度数。
∠A比∠B大20°
∠A=∠B+20°
两个锐角的度数
【典例5】用观察法解决稍复杂的三角形内角度数问题
分析:通过观察可知,正方形的顶点A、B都与线段EF上的点G重合,线段DG和CG是正方形的边,即DG=CG=CD,由此可知,三角形CGD是等边三角形,所以∠1=60。
如图,在正方形ABCD中,E、F分别是线段AB、CD的中点,将正方形的∠A和∠B折起,使顶点A、B都与线段EF上的点G重合,求∠1的度数。
解答:DG=CG=CD
三角形CGD是等边三角形
∠1=180÷3=60°
答:∠1的度数是60°。
模块三:完成变式训练
1.小强家要建一座漂亮的房子,请你帮他选择3根木料做成房子的三角架,并说明你选择的理由。(提示:三角架有两边相等)
分析:在选择木料时,注意房子的三角架有两边是相等的,可以
先确定两根相等的木料,再选择第三根木料。
解答:6、6、3;6+3>6,6+6>3 能摆成三角形
6、6、5;6+5>6,6+6>5 能摆成三角形
3、3、6;3+3=6 不能摆成三角形
3、3、5;3+5>3,3+3>5 能摆成三角形
可以选(6、6、3)或(6、6、5)或(3、3、5)
理由:它们每组的三个数都满足三角形任意两边的和大于第三边,即都能拼成三角形,且有两边相等。
2.陈伯伯家有一块等腰三角形菜地,他用长是18m的篱笆恰好围了一圈。其中一条边长是4m,另外两边分别是多少?
解答:情况一:4m是腰长,那么底边长为18-4×2=10(m)
因为:4+4=8<10,不满足三角形任意两边之和大于第三边,
所以:这种情况不成立。
情况二:4m是底边长,那么腰长为(18-4)÷2=7(m)
此时7+7=14>4,7+4=11>7,满足三角形三边关系,
所以:另外两边分别是7m、7m。
3.在等腰三角形中,较大角是较小角度数的4倍。这个三角形的顶角与底角各是多少度
解答:情况一:较大角是顶角时
180°÷(4+1+1)=30°30°×4=120°
情况二;较大角是底角时
180°÷(4+4+1)=20°20°×4=80°
答:当较大角是顶角时,顶角是120°,底角是30°;当较大角是底角时,顶角是20°,底角是80°。
4.在三角形ABC中,已知∠A=30°,∠B是∠C的2倍,求∠B的度数。
解答:180°-30°=150°
150°÷(2+1)=50°
2×50°=100°
答:∠B的度数是100°。
5.如图,在一张三角形纸片ABC中,∠C=90°,将这张纸片沿线段DE剪去一个角后变成一个四边形ABED,那么图中∠1+∠2等于多少度
解答:∠A+∠B=180°-∠C=180°-90°=90°
∠1+∠2=360°-(∠A+∠B)=360°-90°=270°
答:∠1+∠2等于270°。
