山东省滕州市荆河街道滕南中学2024-2025学年七年级下学期第二学期阶段性质量监测数学试题(4,5章)(含详解)
文档属性
| 名称 | 山东省滕州市荆河街道滕南中学2024-2025学年七年级下学期第二学期阶段性质量监测数学试题(4,5章)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 449.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 21:02:04 | ||
图片预览



文档简介
北师大新版七年级(下)第二次质量检测数学模拟试卷
一、选择题(本大题12小题,每小题3分,共36分)
1.下列四个选项左边图形与右边图形成轴对称的是( )
A. B.
C. D.
2.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
3.如图,已知AB=CD且AB∥CD,点E,F为线段AC上的两点,添加以下条件,不能判定△ABE≌△CDF的是( )
A.BE=DF B.∠AEB=∠CFD C.BE∥DF D.AF=CE
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
5.等腰三角形的一条边长为4,另一条边长为7,则该三角形的周长为( )
A.15 B.18 C.15或18 D.18或23
6.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
7.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
7.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点,作直线交于点,连接,则的周长为( )
A.7 B.8 C.10 D.12
8.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得∠1=40°.则∠2的度数为( )
A.45° B.55° C.65° D.75°
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
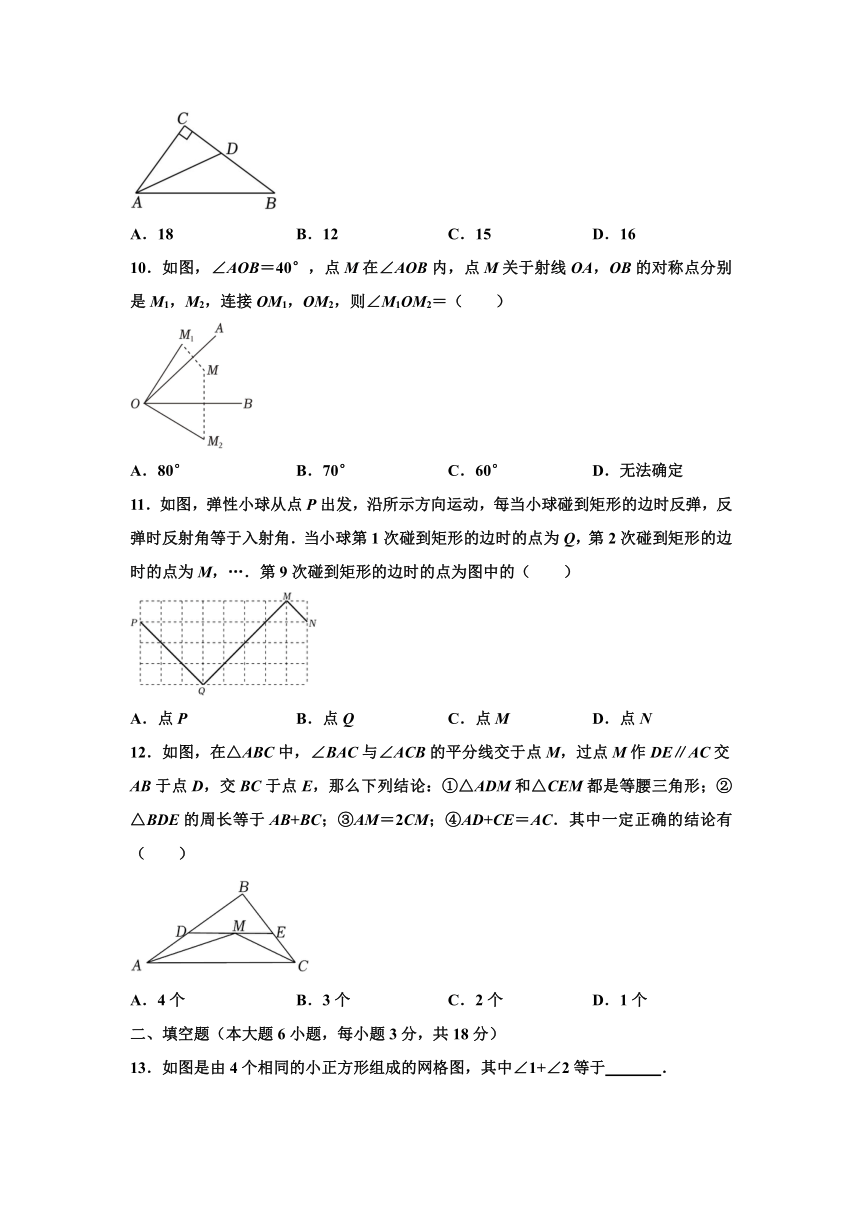
A.18 B.12 C.15 D.16
10.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70° C.60° D.无法确定
11.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第9次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
12.如图,在△ABC中,∠BAC与∠ACB的平分线交于点M,过点M作DE∥AC交AB于点D,交BC于点E,那么下列结论:①△ADM和△CEM都是等腰三角形;②△BDE的周长等于AB+BC;③AM=2CM;④AD+CE=AC.其中一定正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题6小题,每小题3分,共18分)
13.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
14.设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|= .
15.如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为 .
16.如图,△ACB中,∠ACB=90°,∠1=∠B.AC=8,BC=6,AB=10,则CD的长 .
17.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=40cm,OB=30cm,则点C离地面的距离是 cm.
18.如图,矩形的一个顶点落在边长为3的正方形中心(正方形对角线交点),则图中重合部分(阴影部分)的面积为 平方单位.
三、解答题
19.(9分)如图,在每个小正方形的边长都为1的网格中有一个△DEF.
(1)作与△DEF关于直线HG成轴对称的图形(不写作法);
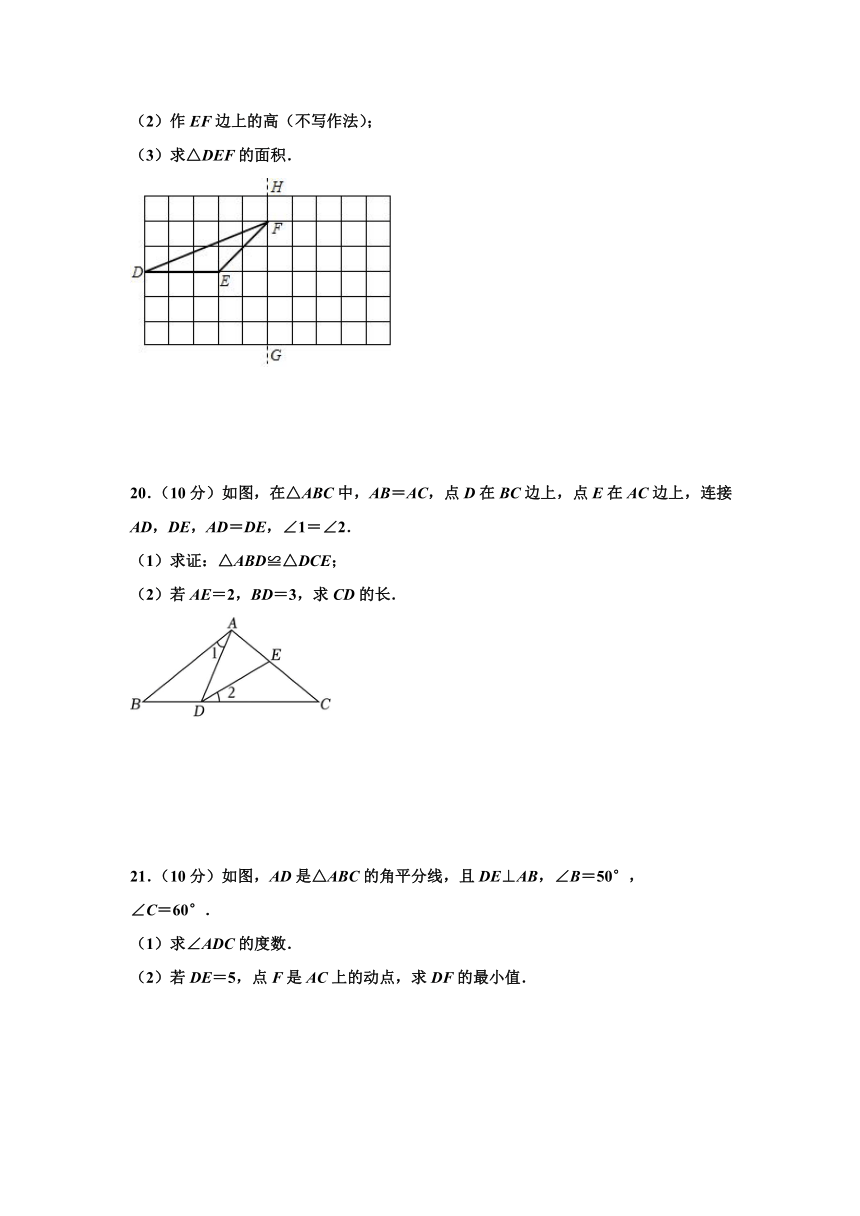
(2)作EF边上的高(不写作法);
(3)求△DEF的面积.
20.(10分)如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD,DE,AD=DE,∠1=∠2.
(1)求证:△ABD≌△DCE;
(2)若AE=2,BD=3,求CD的长.
21.(10分)如图,AD是△ABC的角平分线,且DE⊥AB,∠B=50°,
∠C=60°.
(1)求∠ADC的度数.
(2)若DE=5,点F是AC上的动点,求DF的最小值.
22.(10分)如图,BC=6cm,∠PBC=∠QCB=60°,点M在线段CB上以3cm/s的速度由点C向点B运动,同时,点N在射线CQ上以1cm/s的速度运动,它们运动的时间为t(s)(当点M运动结束时,点N运动随之结束).在射线BP上取点A,在M、N运动到某处时,有△ABM与△MCN全等,求此时AB的长度?
23.(13分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
24.(14分)小丽与爸妈在公园里坐荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是多少?
答案提示
北师大新版七年级(下)第二次质量检测数学模拟试卷
一、选择题(本大题12小题,每小题3分,共36分)
1.下列四个选项左边图形与右边图形成轴对称的是( )
A. B.
C. D.
根据轴对称图形的概念求解.
【解答】解:A、左边图形与右边图形不成轴对称,故本选项不合题意;
B、左边图形与右边图形不成轴对称,故本选项不合题意;
C、左边图形与右边图形不成轴对称,故本选项不合题意;
D、左边图形与右边图形成轴对称,故本选项符合题意.
故选:D.
2.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
根据三角形的稳定性解答即可.
【解答】解:如图所示,
根据三角形具有稳定性,
所以至少还要在架子上钉上的木棒根数是2,
故选:C.
3.如图,已知AB=CD且AB∥CD,点E,F为线段AC上的两点,添加以下条件,不能判定△ABE≌△CDF的是( )
A.BE=DF B.∠AEB=∠CFD C.BE∥DF D.AF=CE
根据全等三角形的判定方法,逐一判断即可解答.
【解答】解:∵AB∥CD,
∴∠A=∠C,
A、∵AB=CD,∠A=∠C,BE=DF,
∴△ABE和△CDF不一定全等,
故A符合题意;
B、∵AB=CD,∠A=∠C,∠AEB=∠CFD,
∴△ABE≌△CDF(AAS),
故B不符合题意;
C、∵BE∥DF,
∴∠BEF=∠DFE,
∵∠BEF+∠AEB=180°,∠DFE+∠CFD=180°,
∴∠AEB=∠CFD,
∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(AAS),
故C不符合题意;
D、∵AF=CE,
∴AF﹣EF=CE﹣EF,
∴AE=CF,
∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(SAS),
故D不符合题意;
故选:A.
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
运用SAS证明△ABD≌△ACE,得∠B=∠C.根据三角形内角和定理可求∠DAE的度数.则易求∠CAE的度数.
【解答】解:如图,∵∠1=∠2=110°,
∴∠ADE=∠AED=70°,
∴∠DAE=180°﹣2°.
∵BE=CD,∴BD=CE.
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS)
∴∠BAD=∠CAE.
∵∠BAE=60°,
∴∠BAD=∠CAE=20°.
故选:A.
5.等腰三角形的一条边长为4,另一条边长为7,则该三角形的周长为( )
A.15 B.18 C.15或18 D.18或23
分为两种情况4为底或7为底,还要注意是否符合三角形三边关系.
【解答】解:∵等腰三角形的一条边长为4,另一条边长为7,
∴有两种情况:
①7为底,4为腰,4+4>7,符合题意,
∴该三角形的周长是4+4+7=15;
②4为底,7为腰,7+4>7,符合题意,
∴该三角形的周长是7+7+4=18.
故选:C.
6.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
由中垂线的性质,即可求解.
【解答】解:∵线段垂直平分线上的点到线段两端的距离相等,
∴要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是△ABC三边的垂直平分线的交点,
故选:C.
7.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
利用面积差可得三角形ABC的面积.
【解答】解:S△ABC=3×3﹣×=.
故选:C.
7.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点,作直线交于点,连接,则的周长为( )
A.7 B.8 C.10 D.12
本题考查了尺规作图—作垂直平分线,根据垂直平分线的性质即可证明,根据的周长,即可求出答案.
解:由作图知,垂直平分,
,
的周长,
,,
的周长,
故选:C.
8.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得∠1=40°.则∠2的度数为( )
A.45° B.55° C.65° D.75°
解:如图,
∠3=180°﹣60°﹣45°=75°,
∠2=180°﹣∠1﹣∠3=180°﹣40°﹣75°=65°,
故选:C.
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据题意求出CD的长即可.
【解答】解:作DE⊥AB于E,
∵BD:CD=3:2,BC=30,
∴CD=12,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴CD=DE=12,
故选:B.
10.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70° C.60° D.无法确定
根据轴对称的性质得出∠MOA=∠M1OA,∠MOB=∠M2OB,即可求解.
【解答】解:连接OM,如图所示,
∵点M关于射线OA,OB的对称点分别是M1,M2,
∴∠MOA=∠M1OA,∠MOB=∠M2OB,
∴∠M1OA+∠M2OB=∠MOA+∠MOB=∠AOB=40°,
∴∠M1OM2=∠M1OA+∠M2OB+∠AOB=40°+40°=80°,
故选:A.
11.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第9次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,进而确定位置即可.
【解答】解:如图所示,小球反弹6次回到点P处,而9﹣6=3,
∴第9次碰到矩形的边时的点为图中的点N.
故选:D.
12.如图,在△ABC中,∠BAC与∠ACB的平分线交于点M,过点M作DE∥AC交AB于点D,交BC于点E,那么下列结论:①△ADM和△CEM都是等腰三角形;②△BDE的周长等于AB+BC;③AM=2CM;④AD+CE=AC.其中一定正确的结论有( )
A.4个 B.3个 C.2个 D.1个
由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.
【解答】解:∵DE∥AC,
∴∠DMA=∠MAC,∠EMC=∠MCA,
∵△ABC中,∠BAC与∠ACB的平分线交于点M,
∴∠DAM=∠MAC,∠ECM=∠MCA,
∴∠DAM=∠DMA,∠EMC=∠ECM,
∴DA=DM,ME=EC,
即△ADM和△CEM都是等腰三角形;
故①正确;
∴DE=DM+EM=AD+CE,
∵AC>DE,
∴AD+CE<AC,故④错误;
∴△BDE的周长为:BD+DE+BE=DB+DM+ME+BE=AB+BC;故②正确;
根据已知条件无法证明AM=2CM,故③错误.
故选:C.
二、填空题(本大题6小题,每小题3分,共18分)
13.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
首先证明△ABC≌△DBE可得∠1=∠ACB,再根据等量代换可得∠1+∠2=180°.
【解答】解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
14.设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|= .
直接利用三角形三边关系结合绝对值的性质分别化简得出答案.
【解答】解:∵a,b,c分别为△ABC的三边,
∴a+b﹣c>0,a﹣c﹣b<0,c﹣a﹣b<0,
∴|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|=a+b﹣c+(a﹣c﹣b)﹣(c﹣a﹣b)
=a+b﹣c+a﹣c﹣b﹣c+a+b
=3a+b﹣3c.
故答案为:3a+b﹣3c.
15.如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为 .
由AB,AC的垂直平分线分别交BC于D,E,垂足分别是M,N,根据线段垂直平分线的性质,可得AD=BD,AE=EC,继而可得△ADE的周长等于BC的长.
【解答】解:因为AB,AC的垂直平分线分别交BC于点D,E,
所以AD=BD,AE=EC,
所以BC=BD+DE+CE=AD+DE+AE,即为△ADE的周长,
又因为△ADE的周长为22,
所以BC=22.
故答案为:22.
16.如图,△ACB中,∠ACB=90°,∠1=∠B.AC=8,BC=6,AB=10,则CD的长 .
解:(1)∵∠ACB=∠CDB=90°
∴S△ABCAC BCAB CD,
∵AC=8,BC=6,AB=10,
∴CD.
17.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=40cm,OB=30cm,则点C离地面的距离是 cm.
如图,过点C作CD⊥OB于点D,构造全等三角形△AOB≌△BDC(AAS),由全等三角形的对应边相等得到OB=CD.
【解答】解:如图,过点C作CD⊥OB于点D,
∵∠O=∠ABC=∠BDC=90°,
∴∠1=∠2(同角的余角相等).
在△AOB与△BDC中,
,
∴△AOB≌△BDC(AAS).
∴OB=CD=30cm.
故答案为:30.
18.如图,矩形的一个顶点落在边长为3的正方形中心(正方形对角线交点),则图中重合部分(阴影部分)的面积为 平方单位.
如图用字母表示各顶点,根据图形和题意可以推出△OBJ≌△OCH,所以重合部分的面积为△OBC的面积
【解答】解:四边形ABCD是正方形,四边形EOFG是矩形,O是正方形的中心.
∵四边形ABCD是正方形,四边形EOFG是矩形.
分别连接OB,OC,
∴∠OBJ=∠OCH=45°,OB=OC,∠BOJ=∠COH=90°﹣∠BOH,
∴△OBJ≌△OCH(ASA).
又∵正方形的边长都为3,
∴OB=OC=,
∴四边形OJHD的面积=S△OJB+S△ODH,
∴四边形OGHD的面积=S△OCH+S△OBH=S△OBC,
∴四边形OJBH的面积=.
故答案为:.
三、解答题
19.(9分)如图,在每个小正方形的边长都为1的网格中有一个△DEF.
(1)作与△DEF关于直线HG成轴对称的图形(不写作法);
(2)作EF边上的高(不写作法);
(3)求△DEF的面积.
(1)分别作出D,E,F的对应点F,N,M即可.
(2)利用数形结合的思想解决问题即可.
(3)利用三角形的面积公式计算即可.
【解答】解:(1)如图,△NMF即为所求.
(2)如图,线段DT即为所求.
(3)S△DEF3×2=3.
20.(10分)如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD,DE,AD=DE,∠1=∠2.
(1)求证:△ABD≌△DCE;
(2)若AE=2,BD=3,求CD的长.
(1)由题意,利用等腰三角形性质,得到∠B=∠C,结合已知条件,得到两三角形全等;
(2)由△ABD≌△DCE,得到CE=BD=3,从而知AC=5,得到结果.
【解答】(1)证明:AB=AC,
∴∠B=∠C,
又∵∠1=∠2,AD=DE,
∴△ABD≌△DCE(AAS);
(2)解:∵△ABD≌△DCE,
∴CE=BD=3,AB=DC,
∵AE=2,
∴AC=CE+AE=3+2=5,
∵AB=AC,
∴AB=5,
∴CD=5.
21.(10分)如图,AD是△ABC的角平分线,且DE⊥AB,∠B=50°,
∠C=60°.
(1)求∠ADC的度数.
(2)若DE=5,点F是AC上的动点,求DF的最小值.
(1)根据三角形内角和求出∠BAC,根据角平分线的定义求出∠BAD,再利用外角的性质求解;
(2)根据垂线段最短得到当DF⊥AC时,DF最小,再利用角平分线的性质求出DF=DE=5.
【解答】解:(1)∵∠B=50°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=70°,
∵AD是△ABC的角平分线,
∴,
∴∠ADC=∠B+∠BAD=85°;
(2)∵点F是AC上的动点,
∴当DF⊥AC时,DF最小,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=5.
三角形外角的性质,解题的关键是熟练掌握基本定理和知识.
22.(10分)如图,BC=6cm,∠PBC=∠QCB=60°,点M在线段CB上以3cm/s的速度由点C向点B运动,同时,点N在射线CQ上以1cm/s的速度运动,它们运动的时间为t(s)(当点M运动结束时,点N运动随之结束).在射线BP上取点A,在M、N运动到某处时,有△ABM与△MCN全等,求此时AB的长度?
解:①若△ABM≌△MCN,则BM=CN,AB=CM,可得:t=6﹣3t,AB=3t,
解得:t=1.5,AB=4.5cm;
②若△ABM≌△NCM,则BM=CM,AB=CN,可得:3t=6﹣3t,AB=t,
解得:t=1,AB=1cm
∴AB的长度为1cm或.
23.(13分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
(1)要证△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.
(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.
【解答】证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
24.(14分)小丽与爸妈在公园里坐荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是多少?
根据全等三角形的性质即可得到结论.
【解答】解:由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
∴△COE≌△OBD(AAS),
∴CE=OD,OE=BD,
∵BD、CE分别为1.4m和1.8m,
∴DE=OD﹣OE=CE﹣BD=1.8﹣1.4=0.4(m),
∵AD=1m,
∴AE=AD+DE=1.4(m),
∴爸爸是在距离地面1.4m的地方接住小丽的.
一、选择题(本大题12小题,每小题3分,共36分)
1.下列四个选项左边图形与右边图形成轴对称的是( )
A. B.
C. D.
2.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
3.如图,已知AB=CD且AB∥CD,点E,F为线段AC上的两点,添加以下条件,不能判定△ABE≌△CDF的是( )
A.BE=DF B.∠AEB=∠CFD C.BE∥DF D.AF=CE
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
5.等腰三角形的一条边长为4,另一条边长为7,则该三角形的周长为( )
A.15 B.18 C.15或18 D.18或23
6.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
7.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
7.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点,作直线交于点,连接,则的周长为( )
A.7 B.8 C.10 D.12
8.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得∠1=40°.则∠2的度数为( )
A.45° B.55° C.65° D.75°
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
10.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70° C.60° D.无法确定
11.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第9次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
12.如图,在△ABC中,∠BAC与∠ACB的平分线交于点M,过点M作DE∥AC交AB于点D,交BC于点E,那么下列结论:①△ADM和△CEM都是等腰三角形;②△BDE的周长等于AB+BC;③AM=2CM;④AD+CE=AC.其中一定正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题6小题,每小题3分,共18分)
13.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
14.设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|= .
15.如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为 .
16.如图,△ACB中,∠ACB=90°,∠1=∠B.AC=8,BC=6,AB=10,则CD的长 .
17.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=40cm,OB=30cm,则点C离地面的距离是 cm.
18.如图,矩形的一个顶点落在边长为3的正方形中心(正方形对角线交点),则图中重合部分(阴影部分)的面积为 平方单位.
三、解答题
19.(9分)如图,在每个小正方形的边长都为1的网格中有一个△DEF.
(1)作与△DEF关于直线HG成轴对称的图形(不写作法);
(2)作EF边上的高(不写作法);
(3)求△DEF的面积.
20.(10分)如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD,DE,AD=DE,∠1=∠2.
(1)求证:△ABD≌△DCE;
(2)若AE=2,BD=3,求CD的长.
21.(10分)如图,AD是△ABC的角平分线,且DE⊥AB,∠B=50°,
∠C=60°.
(1)求∠ADC的度数.
(2)若DE=5,点F是AC上的动点,求DF的最小值.
22.(10分)如图,BC=6cm,∠PBC=∠QCB=60°,点M在线段CB上以3cm/s的速度由点C向点B运动,同时,点N在射线CQ上以1cm/s的速度运动,它们运动的时间为t(s)(当点M运动结束时,点N运动随之结束).在射线BP上取点A,在M、N运动到某处时,有△ABM与△MCN全等,求此时AB的长度?
23.(13分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
24.(14分)小丽与爸妈在公园里坐荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是多少?
答案提示
北师大新版七年级(下)第二次质量检测数学模拟试卷
一、选择题(本大题12小题,每小题3分,共36分)
1.下列四个选项左边图形与右边图形成轴对称的是( )
A. B.
C. D.
根据轴对称图形的概念求解.
【解答】解:A、左边图形与右边图形不成轴对称,故本选项不合题意;
B、左边图形与右边图形不成轴对称,故本选项不合题意;
C、左边图形与右边图形不成轴对称,故本选项不合题意;
D、左边图形与右边图形成轴对称,故本选项符合题意.
故选:D.
2.为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )
A.0根 B.1根 C.2根 D.5根
根据三角形的稳定性解答即可.
【解答】解:如图所示,
根据三角形具有稳定性,
所以至少还要在架子上钉上的木棒根数是2,
故选:C.
3.如图,已知AB=CD且AB∥CD,点E,F为线段AC上的两点,添加以下条件,不能判定△ABE≌△CDF的是( )
A.BE=DF B.∠AEB=∠CFD C.BE∥DF D.AF=CE
根据全等三角形的判定方法,逐一判断即可解答.
【解答】解:∵AB∥CD,
∴∠A=∠C,
A、∵AB=CD,∠A=∠C,BE=DF,
∴△ABE和△CDF不一定全等,
故A符合题意;
B、∵AB=CD,∠A=∠C,∠AEB=∠CFD,
∴△ABE≌△CDF(AAS),
故B不符合题意;
C、∵BE∥DF,
∴∠BEF=∠DFE,
∵∠BEF+∠AEB=180°,∠DFE+∠CFD=180°,
∴∠AEB=∠CFD,
∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(AAS),
故C不符合题意;
D、∵AF=CE,
∴AF﹣EF=CE﹣EF,
∴AE=CF,
∵AB=CD,∠A=∠C,
∴△ABE≌△CDF(SAS),
故D不符合题意;
故选:A.
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
运用SAS证明△ABD≌△ACE,得∠B=∠C.根据三角形内角和定理可求∠DAE的度数.则易求∠CAE的度数.
【解答】解:如图,∵∠1=∠2=110°,
∴∠ADE=∠AED=70°,
∴∠DAE=180°﹣2°.
∵BE=CD,∴BD=CE.
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS)
∴∠BAD=∠CAE.
∵∠BAE=60°,
∴∠BAD=∠CAE=20°.
故选:A.
5.等腰三角形的一条边长为4,另一条边长为7,则该三角形的周长为( )
A.15 B.18 C.15或18 D.18或23
分为两种情况4为底或7为底,还要注意是否符合三角形三边关系.
【解答】解:∵等腰三角形的一条边长为4,另一条边长为7,
∴有两种情况:
①7为底,4为腰,4+4>7,符合题意,
∴该三角形的周长是4+4+7=15;
②4为底,7为腰,7+4>7,符合题意,
∴该三角形的周长是7+7+4=18.
故选:C.
6.如图,是一块三角形的草坪,现要在草坪上建一凉亭,要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是( )
A.△ABC的三条中线的交点 B.△ABC三条角平分线的交点
C.△ABC三边的垂直平分线的交点 D.△ABC三条高所在直线的交点
由中垂线的性质,即可求解.
【解答】解:∵线段垂直平分线上的点到线段两端的距离相等,
∴要使凉亭到草坪三个顶点的距离相等,凉亭应选的位置是△ABC三边的垂直平分线的交点,
故选:C.
7.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,则S△ABC的面积为( )
A. B.3 C. D.4
利用面积差可得三角形ABC的面积.
【解答】解:S△ABC=3×3﹣×=.
故选:C.
7.如图,在中,,,分别以点,点为圆心,大于的长为半径作弧,两弧交于点,,过点,作直线交于点,连接,则的周长为( )
A.7 B.8 C.10 D.12
本题考查了尺规作图—作垂直平分线,根据垂直平分线的性质即可证明,根据的周长,即可求出答案.
解:由作图知,垂直平分,
,
的周长,
,,
的周长,
故选:C.
8.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得∠1=40°.则∠2的度数为( )
A.45° B.55° C.65° D.75°
解:如图,
∠3=180°﹣60°﹣45°=75°,
∠2=180°﹣∠1﹣∠3=180°﹣40°﹣75°=65°,
故选:C.
9.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点D到AB的距离为( )
A.18 B.12 C.15 D.16
作DE⊥AB于E,根据角平分线的性质得到CD=DE,根据题意求出CD的长即可.
【解答】解:作DE⊥AB于E,
∵BD:CD=3:2,BC=30,
∴CD=12,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴CD=DE=12,
故选:B.
10.如图,∠AOB=40°,点M在∠AOB内,点M关于射线OA,OB的对称点分别是M1,M2,连接OM1,OM2,则∠M1OM2=( )
A.80° B.70° C.60° D.无法确定
根据轴对称的性质得出∠MOA=∠M1OA,∠MOB=∠M2OB,即可求解.
【解答】解:连接OM,如图所示,
∵点M关于射线OA,OB的对称点分别是M1,M2,
∴∠MOA=∠M1OA,∠MOB=∠M2OB,
∴∠M1OA+∠M2OB=∠MOA+∠MOB=∠AOB=40°,
∴∠M1OM2=∠M1OA+∠M2OB+∠AOB=40°+40°=80°,
故选:A.
11.如图,弹性小球从点P出发,沿所示方向运动,每当小球碰到矩形的边时反弹,反弹时反射角等于入射角.当小球第1次碰到矩形的边时的点为Q,第2次碰到矩形的边时的点为M,….第9次碰到矩形的边时的点为图中的( )
A.点P B.点Q C.点M D.点N
根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,进而确定位置即可.
【解答】解:如图所示,小球反弹6次回到点P处,而9﹣6=3,
∴第9次碰到矩形的边时的点为图中的点N.
故选:D.
12.如图,在△ABC中,∠BAC与∠ACB的平分线交于点M,过点M作DE∥AC交AB于点D,交BC于点E,那么下列结论:①△ADM和△CEM都是等腰三角形;②△BDE的周长等于AB+BC;③AM=2CM;④AD+CE=AC.其中一定正确的结论有( )
A.4个 B.3个 C.2个 D.1个
由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.
【解答】解:∵DE∥AC,
∴∠DMA=∠MAC,∠EMC=∠MCA,
∵△ABC中,∠BAC与∠ACB的平分线交于点M,
∴∠DAM=∠MAC,∠ECM=∠MCA,
∴∠DAM=∠DMA,∠EMC=∠ECM,
∴DA=DM,ME=EC,
即△ADM和△CEM都是等腰三角形;
故①正确;
∴DE=DM+EM=AD+CE,
∵AC>DE,
∴AD+CE<AC,故④错误;
∴△BDE的周长为:BD+DE+BE=DB+DM+ME+BE=AB+BC;故②正确;
根据已知条件无法证明AM=2CM,故③错误.
故选:C.
二、填空题(本大题6小题,每小题3分,共18分)
13.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于 .
首先证明△ABC≌△DBE可得∠1=∠ACB,再根据等量代换可得∠1+∠2=180°.
【解答】解:由题意得:AB=DB,AC=ED,∠A=∠D=90°,
∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),
∴∠1=∠ACB,
∵∠ACB+∠2=180°,
∴∠1+∠2=180°,
故答案为:180°.
14.设a、b、c是△ABC的三边,化简:|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|= .
直接利用三角形三边关系结合绝对值的性质分别化简得出答案.
【解答】解:∵a,b,c分别为△ABC的三边,
∴a+b﹣c>0,a﹣c﹣b<0,c﹣a﹣b<0,
∴|a+b﹣c|﹣|a﹣c﹣b|+|c﹣a﹣b|=a+b﹣c+(a﹣c﹣b)﹣(c﹣a﹣b)
=a+b﹣c+a﹣c﹣b﹣c+a+b
=3a+b﹣3c.
故答案为:3a+b﹣3c.
15.如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为 .
由AB,AC的垂直平分线分别交BC于D,E,垂足分别是M,N,根据线段垂直平分线的性质,可得AD=BD,AE=EC,继而可得△ADE的周长等于BC的长.
【解答】解:因为AB,AC的垂直平分线分别交BC于点D,E,
所以AD=BD,AE=EC,
所以BC=BD+DE+CE=AD+DE+AE,即为△ADE的周长,
又因为△ADE的周长为22,
所以BC=22.
故答案为:22.
16.如图,△ACB中,∠ACB=90°,∠1=∠B.AC=8,BC=6,AB=10,则CD的长 .
解:(1)∵∠ACB=∠CDB=90°
∴S△ABCAC BCAB CD,
∵AC=8,BC=6,AB=10,
∴CD.
17.如图,一个等腰直角三角形ABC物件斜靠在墙角处(∠O=90°),若OA=40cm,OB=30cm,则点C离地面的距离是 cm.
如图,过点C作CD⊥OB于点D,构造全等三角形△AOB≌△BDC(AAS),由全等三角形的对应边相等得到OB=CD.
【解答】解:如图,过点C作CD⊥OB于点D,
∵∠O=∠ABC=∠BDC=90°,
∴∠1=∠2(同角的余角相等).
在△AOB与△BDC中,
,
∴△AOB≌△BDC(AAS).
∴OB=CD=30cm.
故答案为:30.
18.如图,矩形的一个顶点落在边长为3的正方形中心(正方形对角线交点),则图中重合部分(阴影部分)的面积为 平方单位.
如图用字母表示各顶点,根据图形和题意可以推出△OBJ≌△OCH,所以重合部分的面积为△OBC的面积
【解答】解:四边形ABCD是正方形,四边形EOFG是矩形,O是正方形的中心.
∵四边形ABCD是正方形,四边形EOFG是矩形.
分别连接OB,OC,
∴∠OBJ=∠OCH=45°,OB=OC,∠BOJ=∠COH=90°﹣∠BOH,
∴△OBJ≌△OCH(ASA).
又∵正方形的边长都为3,
∴OB=OC=,
∴四边形OJHD的面积=S△OJB+S△ODH,
∴四边形OGHD的面积=S△OCH+S△OBH=S△OBC,
∴四边形OJBH的面积=.
故答案为:.
三、解答题
19.(9分)如图,在每个小正方形的边长都为1的网格中有一个△DEF.
(1)作与△DEF关于直线HG成轴对称的图形(不写作法);
(2)作EF边上的高(不写作法);
(3)求△DEF的面积.
(1)分别作出D,E,F的对应点F,N,M即可.
(2)利用数形结合的思想解决问题即可.
(3)利用三角形的面积公式计算即可.
【解答】解:(1)如图,△NMF即为所求.
(2)如图,线段DT即为所求.
(3)S△DEF3×2=3.
20.(10分)如图,在△ABC中,AB=AC,点D在BC边上,点E在AC边上,连接AD,DE,AD=DE,∠1=∠2.
(1)求证:△ABD≌△DCE;
(2)若AE=2,BD=3,求CD的长.
(1)由题意,利用等腰三角形性质,得到∠B=∠C,结合已知条件,得到两三角形全等;
(2)由△ABD≌△DCE,得到CE=BD=3,从而知AC=5,得到结果.
【解答】(1)证明:AB=AC,
∴∠B=∠C,
又∵∠1=∠2,AD=DE,
∴△ABD≌△DCE(AAS);
(2)解:∵△ABD≌△DCE,
∴CE=BD=3,AB=DC,
∵AE=2,
∴AC=CE+AE=3+2=5,
∵AB=AC,
∴AB=5,
∴CD=5.
21.(10分)如图,AD是△ABC的角平分线,且DE⊥AB,∠B=50°,
∠C=60°.
(1)求∠ADC的度数.
(2)若DE=5,点F是AC上的动点,求DF的最小值.
(1)根据三角形内角和求出∠BAC,根据角平分线的定义求出∠BAD,再利用外角的性质求解;
(2)根据垂线段最短得到当DF⊥AC时,DF最小,再利用角平分线的性质求出DF=DE=5.
【解答】解:(1)∵∠B=50°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=70°,
∵AD是△ABC的角平分线,
∴,
∴∠ADC=∠B+∠BAD=85°;
(2)∵点F是AC上的动点,
∴当DF⊥AC时,DF最小,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=5.
三角形外角的性质,解题的关键是熟练掌握基本定理和知识.
22.(10分)如图,BC=6cm,∠PBC=∠QCB=60°,点M在线段CB上以3cm/s的速度由点C向点B运动,同时,点N在射线CQ上以1cm/s的速度运动,它们运动的时间为t(s)(当点M运动结束时,点N运动随之结束).在射线BP上取点A,在M、N运动到某处时,有△ABM与△MCN全等,求此时AB的长度?
解:①若△ABM≌△MCN,则BM=CN,AB=CM,可得:t=6﹣3t,AB=3t,
解得:t=1.5,AB=4.5cm;
②若△ABM≌△NCM,则BM=CM,AB=CN,可得:3t=6﹣3t,AB=t,
解得:t=1,AB=1cm
∴AB的长度为1cm或.
23.(13分)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.
(1)要证△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.
(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.
【解答】证明:(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,
∴BD=CE;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,
∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,
则BD⊥CE.
24.(14分)小丽与爸妈在公园里坐荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是多少?
根据全等三角形的性质即可得到结论.
【解答】解:由题意可知∠CEO=∠BDO=90°,OB=OC,
∵∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°.
∴∠COE=∠OBD,
在△COE和△OBD中,
∴△COE≌△OBD(AAS),
∴CE=OD,OE=BD,
∵BD、CE分别为1.4m和1.8m,
∴DE=OD﹣OE=CE﹣BD=1.8﹣1.4=0.4(m),
∵AD=1m,
∴AE=AD+DE=1.4(m),
∴爸爸是在距离地面1.4m的地方接住小丽的.
同课章节目录
