陕西省西安市碑林区铁一中学2024-2025学年下学期七年级第二次月考数学试卷(含详解)
文档属性
| 名称 | 陕西省西安市碑林区铁一中学2024-2025学年下学期七年级第二次月考数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 861.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 20:39:41 | ||
图片预览



文档简介
2024-2025学年陕西省西安市碑林区铁一中学七年级(下)第二次月考数学试卷
一.选择题
1.已知甲型流感病毒直径约为0.000000081米,把0.000000081用科学记数法表示为( )
A.8.1×10﹣7 B.8.1×10﹣8 C.8.1×10﹣9 D.﹣8.1×10﹣9
2.下列图案中,不属于轴对称图形的是( )
A. B. C. D.
3.下列选项中是随机事件的是( )
A.水从高处往低处流动
B.任意画一个三角形,其内角和是180°
C.煮熟的种子发芽
D.星期天下雨
4.如图所示,将直尺与含60°角的直角三角板叠放在一起,若∠1=70°,则∠2的度数为( )
A.70° B.60° C.50° D.30°
5.若(x+2)(x﹣1)=x2+mx+n,则m+n=( )
A.1 B.﹣2 C.﹣1 D.2
6.如图是一个可以自由转动的转盘.转动转盘,当指针停止转动时,指针落在红色区域的概率是( )
A.1 B. C. D.
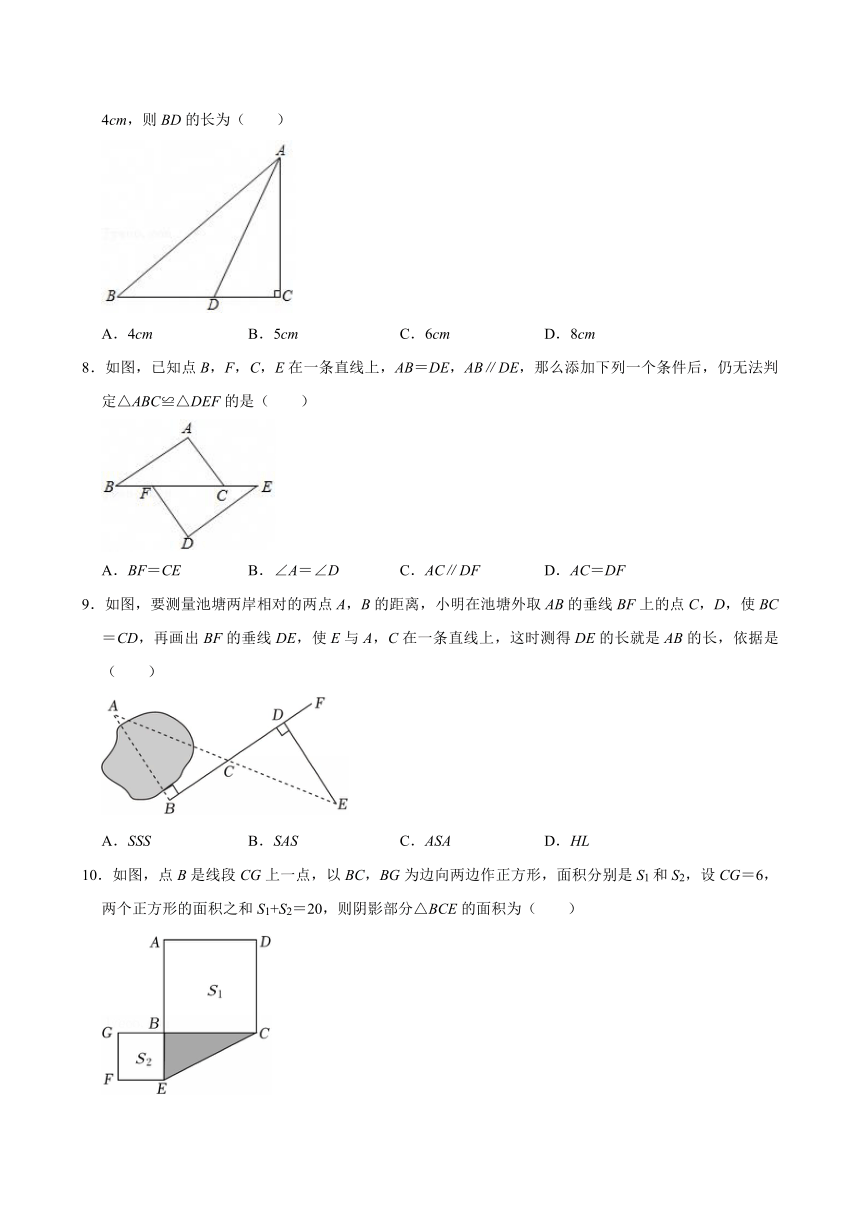
7.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=10cm,点D到AB的距离为4cm,则BD的长为( )
A.4cm B.5cm C.6cm D.8cm
8.如图,已知点B,F,C,E在一条直线上,AB=DE,AB∥DE,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.BF=CE B.∠A=∠D C.AC∥DF D.AC=DF
9.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
10.如图,点B是线段CG上一点,以BC,BG为边向两边作正方形,面积分别是S1和S2,设CG=6,两个正方形的面积之和S1+S2=20,则阴影部分△BCE的面积为( )
A.4 B.5 C.8 D.10
二.填空题
11.2﹣4= .
12.如图,在2×2的正方形网格中,∠1+∠2= .
13.已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的周长是 .
14.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 度.
15.已知△ABC中,AD为BC边上的高,若AD=4,BD=9,CD=5,则△ABC的面积为 .
16.如图,在四边形ABCD中,BA=BC,对角线BD是∠ADC的平分线,若∠ADC=60°,DC=3,∠ABD=3∠CBD,则AD= .
三.解答题
17.计算:
(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab);
(2)(﹣1)2024+(﹣3)+(π+5)0﹣();
(3)38.92﹣2×48.9×38.9+48.92;
(4)20252﹣2027×2023.
18.先化简,再求值:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a),其中,b=2.
19.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)
20.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
21.一个不透明的盒子中装有3个白球,2个黄球,1个红球,这些球除颜色外形状和大小完全一样.
(1)在上述盒子中再放入n个形状和大小完全相同的红球,小颖同学从盒子中任意摸出一个球,摸到黄球的概率为,则n= .
(2)在(1)的条件下,小颖和小英同学一起做游戏,小颖从上述盒子中任意摸一个球,如果摸到红球,小颖获胜,否则小英获胜.这个游戏对双方公平吗?为什么?(利用概率的知识进行说明)
22.如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE,∠BAD=∠CAE=90°,连接BE,CD,猜想BE与CD的关系,并证明.
23.【问题发现】
(1)如图①,在△PAB中,过点P作MN⊥AB,垂足为点C,且AC=BC.若PB=6,则PA的值为 ;
【问题探究】
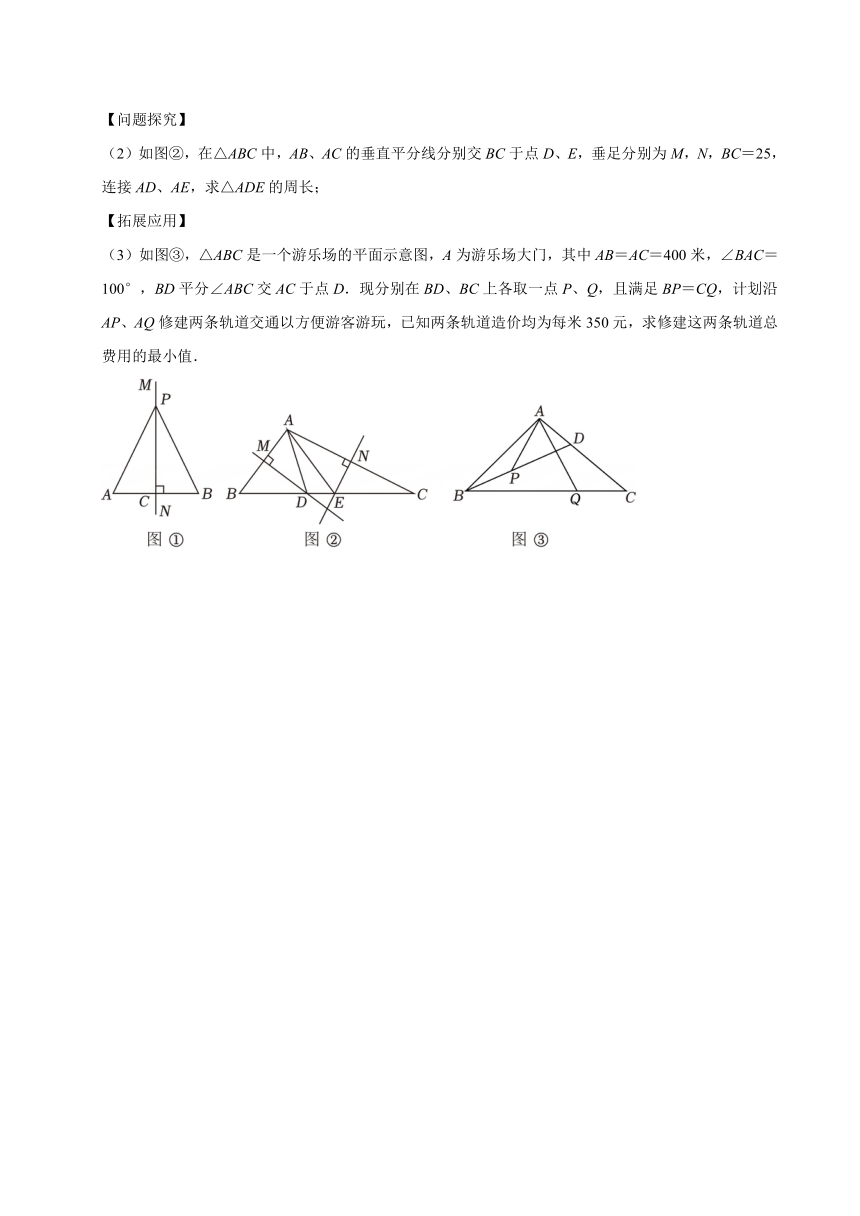
(2)如图②,在△ABC中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,BC=25,连接AD、AE,求△ADE的周长;
【拓展应用】
(3)如图③,△ABC是一个游乐场的平面示意图,A为游乐场大门,其中AB=AC=400米,∠BAC=100°,BD平分∠ABC交AC于点D.现分别在BD、BC上各取一点P、Q,且满足BP=CQ,计划沿AP、AQ修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米350元,求修建这两条轨道总费用的最小值.
2024-2025学年陕西省西安市碑林区铁一中学七年级(下)第二次月考数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C C D C D C A
二.填空题
11.2﹣4= .
【解答】解:原式
.
故答案为:.
12.如图,在2×2的正方形网格中,∠1+∠2= 90° .
【解答】解:如图,
由题意知,在△BAC和△EAD中,
,
∴△BAC≌△EAD(SAS),
∴∠ABC=∠1,
∵∠ABC+∠2=90°,
∴∠1+∠2=90°,
故答案为:90°.
13.已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的周长是 27 .
【解答】解:∵|a﹣5|+(b﹣11)2=0,
∴a﹣5=0,b﹣11=0,
解得:a=5,b=11,
又∵a,b是等腰△ABC的两边长,
∴当b是腰,a是底时,△ABC三边长分别为:11,11,5,
∴该等腰三角形的周长为:11+11+5=27,
当a是腰,b是底时,△ABC三边长分别为:5,5,11,
∵5+5=10<11,
∴不满足三角形三边关系,应舍去.
故答案为:27.
14.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 54 度.
【解答】解:∵∠AOD':∠D'OG=4:3,
设∠AOD'=4x,则∠D'OG=3x,
由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,
即10x=180°,
解得x=18°,
∵AD∥BC,
∴∠BGO=∠DOG=3x=54°,
故答案为:54.
15.已知△ABC中,AD为BC边上的高,若AD=4,BD=9,CD=5,则△ABC的面积为 28或8 .
【解答】解:如图,当AD在三角形ABC内部时,
则BC=BD+CD=9+5=14,
△ABC的面积28;
当AD在三角形ABC外部时,
BC'=BD﹣C'D=9﹣5=4,
则△ABC的面积8,
故答案为:28或8.
16.如图,在四边形ABCD中,BA=BC,对角线BD是∠ADC的平分线,若∠ADC=60°,DC=3,∠ABD=3∠CBD,则AD= 6 .
【解答】解:如图,延长DC至E,使DE=AD,连接BE,
∵BD是∠ADC的平分线,
∴∠ADB=∠EDBADC=30°,
在△ADB和△EDB中,
,
∴△ADB≌△EDB(SAS),
∴∠ABD=∠EBD,∠A=∠E,AB=EB,
∵AB=BC,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠A,
设∠BCE=∠E=∠A=β,
∵∠ABD=3∠CBD,
设∠CBD=α,
∴∠ABD=3∠CBD=3α,
∴∠ABD=∠EBD=3α,
∴∠EBC=2α,
∵∠E+∠BCE+∠EBC=180°,
∴β+β+2α=180°,
∴β+α=90°,
∵∠ADC=60°,
在四边形DABE中,∠E+∠ABE+∠A+∠EDA=360°,
∴β+6α+β+60°=360°,
∴β+3α=150°,
∴α=30°,β=60°,
∴∠ABD=3α=90°,
∴A,B,E在一条直线上
∵∠CDB=∠CBD=30°,
∴BC=DC=3,
∵∠BCE=∠E=β=60°,
∴△BCE是等边三角形,
∴CE=BC=DC=3,
∴AD=DE=DC+CE=6,
故答案为:6.
三.解答题
17.计算:
(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab);
(2)(﹣1)2024+(﹣3)+(π+5)0﹣();
(3)38.92﹣2×48.9×38.9+48.92;
(4)20252﹣2027×2023.
【解答】解:(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab)
=4a4b2+3a4b2+a4b2
=8a4b2;
(2)(﹣1)2024+(﹣3)+(π+5)0﹣()
=1﹣3+1+0.5
=﹣0.5;
(3)38.92﹣2×48.9×38.9+48.92
=(38.9﹣48.9)2
=100;
(4)20252﹣2027×2023
=20252﹣20252+4
=4.
18.先化简,再求值:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a),其中,b=2.
【解答】解:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a)
=(4a2﹣4ab+b2﹣b2+4a2)÷(﹣4a)
=(8a2﹣4ab)÷(﹣4a)
=﹣2a+b,
当a,b=2时,
原式=﹣2×()+2
=1+2
=3.
19.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)
【解答】解:如图,点P即为所求.
20.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
【解答】解:(1)b(2a+3b)+b(4a+3b)﹣b2
=2ab+3b2+4ab+3b2﹣b2
=6ab+5b2(平方米).
答:通道的面积是(6ab+5b2)平方米.
(2)(4a+3b)(2a+3b)﹣(6ab+5b2)
=8a2+6ab+12ab+9b2﹣6ab﹣5b2
=8a2+12ab+4b2(平方米),
答:剩余草坪的面积是(8a2+12ab+4b2)平方米.
21.一个不透明的盒子中装有3个白球,2个黄球,1个红球,这些球除颜色外形状和大小完全一样.
(1)在上述盒子中再放入n个形状和大小完全相同的红球,小颖同学从盒子中任意摸出一个球,摸到黄球的概率为,则n= 4 .
(2)在(1)的条件下,小颖和小英同学一起做游戏,小颖从上述盒子中任意摸一个球,如果摸到红球,小颖获胜,否则小英获胜.这个游戏对双方公平吗?为什么?(利用概率的知识进行说明)
【解答】解:(1)根据题意,得,
解得n=4,
经检验n=4是方程的解,
所以n=4;
故答案为:4;
(4)公平,
P(小颖获胜),P(小英获胜),
∵,
∴公平.
22.如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE,∠BAD=∠CAE=90°,连接BE,CD,猜想BE与CD的关系,并证明.
【解答】解:BE=CD,BE⊥CD,理由如下:
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,
∵∠BAD=∠CAE=90°,
∴∠BAD+∠CAB=∠CAE+∠CAB,即∠BAE=∠CAD,
在△CAD和△EAB中,
,
∴△CAD≌△EAB(SAS),
∴CD=BE,∠ACD=∠AEB,
设BE与CD交于点O,AC与BE交于点F,
∵∠AFE=∠OFC,
∴∠COF=∠CAE=90°,
∴BE⊥CD.
23.【问题发现】
(1)如图①,在△PAB中,过点P作MN⊥AB,垂足为点C,且AC=BC.若PB=6,则PA的值为 6 ;
【问题探究】
(2)如图②,在△ABC中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,BC=25,连接AD、AE,求△ADE的周长;
【拓展应用】
(3)如图③,△ABC是一个游乐场的平面示意图,A为游乐场大门,其中AB=AC=400米,∠BAC=100°,BD平分∠ABC交AC于点D.现分别在BD、BC上各取一点P、Q,且满足BP=CQ,计划沿AP、AQ修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米350元,求修建这两条轨道总费用的最小值.
【解答】解:(1)∵MN⊥AB,
∴∠PCA=∠PCB=90°,
在△ACP和△BCP中,
,
∴△ACP≌△BCP(SAS),
∴PA=PB=6,
故答案为:6;
(2)∵AB、AC的垂直平分线分别交BC于点D、E,
∴AD=BD,CE=AE,
∴△ADE的周长为AD+DE+AE=BD+DE+EC=BC=25;
(3)∵AB=AC,∠BAC=100°,
∴∠ABC=∠ACB=40°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=20°,
如图③:作线段CE,使∠ECQ=∠PBA=20°,EC=AB,连接QE,AE,
∴∠ACE=∠ACB+∠ECQ=40°+20°=60°,
∵AB=AC,EC=AB,
∴AC=EC,
∴△ACE是等边三角形,
∴EC=AE,
∴AB=AE,
在△ECQ和△ABP中,
,
∴△ECQ≌△ABP(SAS),
∴QE=AP,
∴AP+AQ=QE+AQ≥AE,
∴AP+AQ的最小值为AE,
∴AE=AB=400米,
∵两条轨道造价均为每米350元,
∴修建这两条轨道总费用的最小值为400×350=14000(元).
答:修建这两条轨道总费用的最小值为14000元.
一.选择题
1.已知甲型流感病毒直径约为0.000000081米,把0.000000081用科学记数法表示为( )
A.8.1×10﹣7 B.8.1×10﹣8 C.8.1×10﹣9 D.﹣8.1×10﹣9
2.下列图案中,不属于轴对称图形的是( )
A. B. C. D.
3.下列选项中是随机事件的是( )
A.水从高处往低处流动
B.任意画一个三角形,其内角和是180°
C.煮熟的种子发芽
D.星期天下雨
4.如图所示,将直尺与含60°角的直角三角板叠放在一起,若∠1=70°,则∠2的度数为( )
A.70° B.60° C.50° D.30°
5.若(x+2)(x﹣1)=x2+mx+n,则m+n=( )
A.1 B.﹣2 C.﹣1 D.2
6.如图是一个可以自由转动的转盘.转动转盘,当指针停止转动时,指针落在红色区域的概率是( )
A.1 B. C. D.
7.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=10cm,点D到AB的距离为4cm,则BD的长为( )
A.4cm B.5cm C.6cm D.8cm
8.如图,已知点B,F,C,E在一条直线上,AB=DE,AB∥DE,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.BF=CE B.∠A=∠D C.AC∥DF D.AC=DF
9.如图,要测量池塘两岸相对的两点A,B的距离,小明在池塘外取AB的垂线BF上的点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长,依据是( )
A.SSS B.SAS C.ASA D.HL
10.如图,点B是线段CG上一点,以BC,BG为边向两边作正方形,面积分别是S1和S2,设CG=6,两个正方形的面积之和S1+S2=20,则阴影部分△BCE的面积为( )
A.4 B.5 C.8 D.10
二.填空题
11.2﹣4= .
12.如图,在2×2的正方形网格中,∠1+∠2= .
13.已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的周长是 .
14.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 度.
15.已知△ABC中,AD为BC边上的高,若AD=4,BD=9,CD=5,则△ABC的面积为 .
16.如图,在四边形ABCD中,BA=BC,对角线BD是∠ADC的平分线,若∠ADC=60°,DC=3,∠ABD=3∠CBD,则AD= .
三.解答题
17.计算:
(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab);
(2)(﹣1)2024+(﹣3)+(π+5)0﹣();
(3)38.92﹣2×48.9×38.9+48.92;
(4)20252﹣2027×2023.
18.先化简,再求值:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a),其中,b=2.
19.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)
20.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
21.一个不透明的盒子中装有3个白球,2个黄球,1个红球,这些球除颜色外形状和大小完全一样.
(1)在上述盒子中再放入n个形状和大小完全相同的红球,小颖同学从盒子中任意摸出一个球,摸到黄球的概率为,则n= .
(2)在(1)的条件下,小颖和小英同学一起做游戏,小颖从上述盒子中任意摸一个球,如果摸到红球,小颖获胜,否则小英获胜.这个游戏对双方公平吗?为什么?(利用概率的知识进行说明)
22.如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE,∠BAD=∠CAE=90°,连接BE,CD,猜想BE与CD的关系,并证明.
23.【问题发现】
(1)如图①,在△PAB中,过点P作MN⊥AB,垂足为点C,且AC=BC.若PB=6,则PA的值为 ;
【问题探究】
(2)如图②,在△ABC中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,BC=25,连接AD、AE,求△ADE的周长;
【拓展应用】
(3)如图③,△ABC是一个游乐场的平面示意图,A为游乐场大门,其中AB=AC=400米,∠BAC=100°,BD平分∠ABC交AC于点D.现分别在BD、BC上各取一点P、Q,且满足BP=CQ,计划沿AP、AQ修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米350元,求修建这两条轨道总费用的最小值.
2024-2025学年陕西省西安市碑林区铁一中学七年级(下)第二次月考数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B B D C C D C D C A
二.填空题
11.2﹣4= .
【解答】解:原式
.
故答案为:.
12.如图,在2×2的正方形网格中,∠1+∠2= 90° .
【解答】解:如图,
由题意知,在△BAC和△EAD中,
,
∴△BAC≌△EAD(SAS),
∴∠ABC=∠1,
∵∠ABC+∠2=90°,
∴∠1+∠2=90°,
故答案为:90°.
13.已知a、b为等腰△ABC的边长,且满足|a﹣5|+(b﹣11)2=0,则△ABC的周长是 27 .
【解答】解:∵|a﹣5|+(b﹣11)2=0,
∴a﹣5=0,b﹣11=0,
解得:a=5,b=11,
又∵a,b是等腰△ABC的两边长,
∴当b是腰,a是底时,△ABC三边长分别为:11,11,5,
∴该等腰三角形的周长为:11+11+5=27,
当a是腰,b是底时,△ABC三边长分别为:5,5,11,
∵5+5=10<11,
∴不满足三角形三边关系,应舍去.
故答案为:27.
14.如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO= 54 度.
【解答】解:∵∠AOD':∠D'OG=4:3,
设∠AOD'=4x,则∠D'OG=3x,
由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,
即10x=180°,
解得x=18°,
∵AD∥BC,
∴∠BGO=∠DOG=3x=54°,
故答案为:54.
15.已知△ABC中,AD为BC边上的高,若AD=4,BD=9,CD=5,则△ABC的面积为 28或8 .
【解答】解:如图,当AD在三角形ABC内部时,
则BC=BD+CD=9+5=14,
△ABC的面积28;
当AD在三角形ABC外部时,
BC'=BD﹣C'D=9﹣5=4,
则△ABC的面积8,
故答案为:28或8.
16.如图,在四边形ABCD中,BA=BC,对角线BD是∠ADC的平分线,若∠ADC=60°,DC=3,∠ABD=3∠CBD,则AD= 6 .
【解答】解:如图,延长DC至E,使DE=AD,连接BE,
∵BD是∠ADC的平分线,
∴∠ADB=∠EDBADC=30°,
在△ADB和△EDB中,
,
∴△ADB≌△EDB(SAS),
∴∠ABD=∠EBD,∠A=∠E,AB=EB,
∵AB=BC,
∴BE=BC,
∴∠BCE=∠E,
∴∠BCE=∠E=∠A,
设∠BCE=∠E=∠A=β,
∵∠ABD=3∠CBD,
设∠CBD=α,
∴∠ABD=3∠CBD=3α,
∴∠ABD=∠EBD=3α,
∴∠EBC=2α,
∵∠E+∠BCE+∠EBC=180°,
∴β+β+2α=180°,
∴β+α=90°,
∵∠ADC=60°,
在四边形DABE中,∠E+∠ABE+∠A+∠EDA=360°,
∴β+6α+β+60°=360°,
∴β+3α=150°,
∴α=30°,β=60°,
∴∠ABD=3α=90°,
∴A,B,E在一条直线上
∵∠CDB=∠CBD=30°,
∴BC=DC=3,
∵∠BCE=∠E=β=60°,
∴△BCE是等边三角形,
∴CE=BC=DC=3,
∴AD=DE=DC+CE=6,
故答案为:6.
三.解答题
17.计算:
(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab);
(2)(﹣1)2024+(﹣3)+(π+5)0﹣();
(3)38.92﹣2×48.9×38.9+48.92;
(4)20252﹣2027×2023.
【解答】解:(1)(2a2b)2+ab2 3a3﹣a5b3÷(﹣ab)
=4a4b2+3a4b2+a4b2
=8a4b2;
(2)(﹣1)2024+(﹣3)+(π+5)0﹣()
=1﹣3+1+0.5
=﹣0.5;
(3)38.92﹣2×48.9×38.9+48.92
=(38.9﹣48.9)2
=100;
(4)20252﹣2027×2023
=20252﹣20252+4
=4.
18.先化简,再求值:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a),其中,b=2.
【解答】解:[(2a﹣b)2﹣(2a+b)(b﹣2a)]÷(﹣4a)
=(4a2﹣4ab+b2﹣b2+4a2)÷(﹣4a)
=(8a2﹣4ab)÷(﹣4a)
=﹣2a+b,
当a,b=2时,
原式=﹣2×()+2
=1+2
=3.
19.如图,已知△ABC,AC>AB,∠C=45°.请用尺规作图法,在AC边上求作一点P,使∠PBC=45°.(保留作图痕迹.不写作法)
【解答】解:如图,点P即为所求.
20.如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?
【解答】解:(1)b(2a+3b)+b(4a+3b)﹣b2
=2ab+3b2+4ab+3b2﹣b2
=6ab+5b2(平方米).
答:通道的面积是(6ab+5b2)平方米.
(2)(4a+3b)(2a+3b)﹣(6ab+5b2)
=8a2+6ab+12ab+9b2﹣6ab﹣5b2
=8a2+12ab+4b2(平方米),
答:剩余草坪的面积是(8a2+12ab+4b2)平方米.
21.一个不透明的盒子中装有3个白球,2个黄球,1个红球,这些球除颜色外形状和大小完全一样.
(1)在上述盒子中再放入n个形状和大小完全相同的红球,小颖同学从盒子中任意摸出一个球,摸到黄球的概率为,则n= 4 .
(2)在(1)的条件下,小颖和小英同学一起做游戏,小颖从上述盒子中任意摸一个球,如果摸到红球,小颖获胜,否则小英获胜.这个游戏对双方公平吗?为什么?(利用概率的知识进行说明)
【解答】解:(1)根据题意,得,
解得n=4,
经检验n=4是方程的解,
所以n=4;
故答案为:4;
(4)公平,
P(小颖获胜),P(小英获胜),
∵,
∴公平.
22.如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE,∠BAD=∠CAE=90°,连接BE,CD,猜想BE与CD的关系,并证明.
【解答】解:BE=CD,BE⊥CD,理由如下:
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,
∵∠BAD=∠CAE=90°,
∴∠BAD+∠CAB=∠CAE+∠CAB,即∠BAE=∠CAD,
在△CAD和△EAB中,
,
∴△CAD≌△EAB(SAS),
∴CD=BE,∠ACD=∠AEB,
设BE与CD交于点O,AC与BE交于点F,
∵∠AFE=∠OFC,
∴∠COF=∠CAE=90°,
∴BE⊥CD.
23.【问题发现】
(1)如图①,在△PAB中,过点P作MN⊥AB,垂足为点C,且AC=BC.若PB=6,则PA的值为 6 ;
【问题探究】
(2)如图②,在△ABC中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,BC=25,连接AD、AE,求△ADE的周长;
【拓展应用】
(3)如图③,△ABC是一个游乐场的平面示意图,A为游乐场大门,其中AB=AC=400米,∠BAC=100°,BD平分∠ABC交AC于点D.现分别在BD、BC上各取一点P、Q,且满足BP=CQ,计划沿AP、AQ修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米350元,求修建这两条轨道总费用的最小值.
【解答】解:(1)∵MN⊥AB,
∴∠PCA=∠PCB=90°,
在△ACP和△BCP中,
,
∴△ACP≌△BCP(SAS),
∴PA=PB=6,
故答案为:6;
(2)∵AB、AC的垂直平分线分别交BC于点D、E,
∴AD=BD,CE=AE,
∴△ADE的周长为AD+DE+AE=BD+DE+EC=BC=25;
(3)∵AB=AC,∠BAC=100°,
∴∠ABC=∠ACB=40°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=20°,
如图③:作线段CE,使∠ECQ=∠PBA=20°,EC=AB,连接QE,AE,
∴∠ACE=∠ACB+∠ECQ=40°+20°=60°,
∵AB=AC,EC=AB,
∴AC=EC,
∴△ACE是等边三角形,
∴EC=AE,
∴AB=AE,
在△ECQ和△ABP中,
,
∴△ECQ≌△ABP(SAS),
∴QE=AP,
∴AP+AQ=QE+AQ≥AE,
∴AP+AQ的最小值为AE,
∴AE=AB=400米,
∵两条轨道造价均为每米350元,
∴修建这两条轨道总费用的最小值为400×350=14000(元).
答:修建这两条轨道总费用的最小值为14000元.
同课章节目录
