3.1.2 椭圆的几何性质 2024-2025学年高二数学苏教版(2019)选择性必修1
文档属性
| 名称 | 3.1.2 椭圆的几何性质 2024-2025学年高二数学苏教版(2019)选择性必修1 |

|
|
| 格式 | docx | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览




文档简介
3.1.2 椭圆的几何性质 (1)
1. 熟悉椭圆的几何性质(范围,对称性,顶点,离心率).
2. 理解离心率的大小对椭圆形状的影响.
3. 通过数形结合、观察分析、归纳出椭圆的几何性质,进一步体会数形结合的思想.
活动一 掌握椭圆的几何性质
复习巩固:椭圆的定义及其标准方程:
探究:结合椭圆的标准方程+=1(a>b>0)来探究椭圆的几何性质.
1. 范围
思考1
将椭圆的标准方程进行变形,移项得=1-,你能探索出x的取值范围吗?类比能求出y的取值范围吗?
2. 对称性
思考2
在椭圆的标准方程中,将x换成-x,或将y换成-y,或同时把x,y分别换成-x,-y时,方程是否发生变化?这说明什么样的问题?
3. 顶点
思考3
根据方程写出椭圆与坐标轴的交点坐标.
结论:椭圆的顶点:
椭圆的长轴长:
椭圆的短轴长:
结合图形,思考a,b,c的几何意义分别为什么?
4. 离心率
完成下列两个实验:
(1) 将细绳的两端点固定在焦点处,用铅笔笔尖拉紧绳子,在平面上画一个椭圆,然后调整绳子的长度(分别加长、缩短),观察椭圆“扁”的程度的变化规律;
(2) 细绳的长度固定不变,将焦距分别增大或缩小,观察椭圆“扁”的程度的变化规律.
思考4
圆的形状都是相同的,而有些椭圆却比较“扁”,有些椭圆比较“圆”,用什么样的量来刻画椭圆“扁”的程度?
定义:焦距与长轴长的比叫作椭圆的离心率.
探究:椭圆的离心率的取值范围是什么?
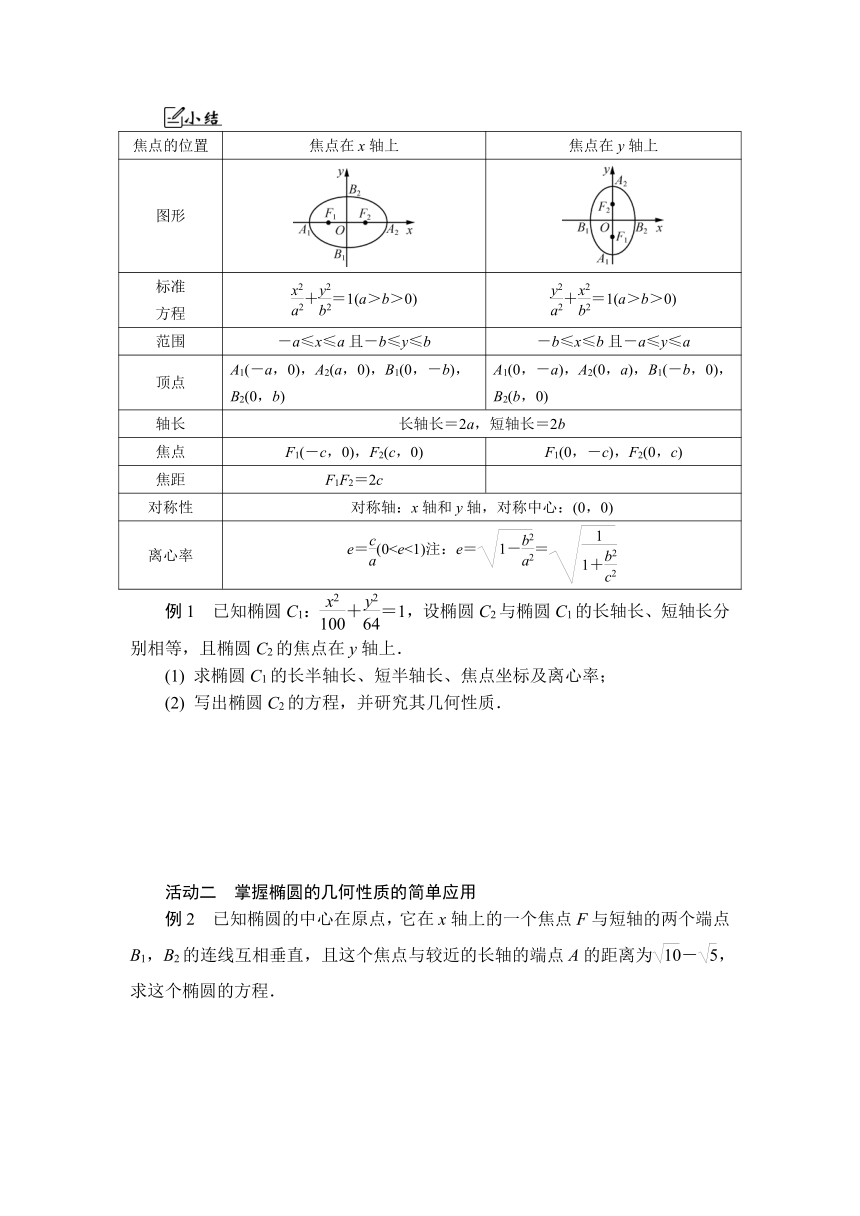
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程 +=1(a>b>0) +=1(a>b>0)
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0),B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)
轴长 长轴长=2a,短轴长=2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 F1F2=2c
对称性 对称轴:x轴和y轴,对称中心:(0,0)
离心率 e=(0例1 已知椭圆C1:+=1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1) 求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2) 写出椭圆C2的方程,并研究其几何性质.
活动二 掌握椭圆的几何性质的简单应用
例2 已知椭圆的中心在原点,它在x轴上的一个焦点F与短轴的两个端点B1,B2的连线互相垂直,且这个焦点与较近的长轴的端点A的距离为-,求这个椭圆的方程.
1. (2024通州、启东、如东等地期末)若椭圆+=1(a>)的离心率为,则a的值为( )
A. 2 B. 2 C. 2 D. 4
2. (2025广东东莞期末)已知边长为2的正方形的四个顶点恰好是椭圆的左、右焦点和短轴两个端点,则椭圆的标准方程为( )
A. +=1 B. +y2=1 C. +=1 D. +=1
3. (多选)若椭圆C:+=1的一个焦点坐标为(0,1),则下列结论中正确的是( )
A. m=2 B. 椭圆C的长轴长为
C. 椭圆C的短轴长为2 D. 椭圆C的离心率为
4. (2024南通中学月考)已知P为椭圆C:+y2=1上一点,A(1,0),则PA的最小值为________.
5. 求适合下列条件的椭圆的标准方程:
(1) 长轴长为6,离心率为;
(2) 经过点P(3,0),离心率为,焦点在x轴上.
3.1.2 椭圆的几何性质 (2)
1. 巩固椭圆简单的几何性质.
2. 能运用椭圆的方程和几何性质处理一些简单的实际问题.
活动一 利用椭圆的性质求椭圆方程
例1 已知椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一个正三角形,焦点在y轴上,且a-c=,求椭圆的方程.
思考1
利用椭圆的几何性质求标准方程的思路是什么?
例2 求适合下列条件的椭圆的标准方程:
(1) 椭圆过点(3,0),离心率e=;
(2) 经过点M(1,2),且与椭圆+=1有相同的离心率;
(3) 在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
活动二 理解椭圆的离心率
例3 设椭圆的两个焦点分别为F1,F2,过点F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
例4 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,椭圆C上存在点P,使∠F1PF2为钝角,则椭圆C离心率的取值范围是________.
思考2
求椭圆离心率及范围的方法有哪些?
(1) 已知椭圆E:+=1(a>b>0)的短轴的两个端点分别为A,B,C为椭圆上异于A,B的一点,直线AC与直线BC的斜率之积为-,则椭圆的离心率为( )
A. B. C. D.
(2) 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆C上的一点,PF2⊥F1F2,∠PF1F2=30°,则椭圆C的离心率为________.
活动三 掌握椭圆的几何性质在实际问题中的应用
例5 如图,我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)F2为一个焦点的椭圆.已知它的近地点A(长轴端点中离地面最近的点)距地面439 km, 远地点B(长轴端点中离地面最远的点)距地面2 384 km,AB是椭圆的长轴,地球的半径约为6371 km.求卫星运行的轨道方程.(精确到1 km)
解决实际问题时,首先要建立适当的平面直角坐标系,然后利用椭圆的几何性质求椭圆的标准方程,通常采用待定系数法,其步骤是:
(1) 建系;
(2) 确定焦点位置;
(3) 设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(4) 根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
1. 已知椭圆+=1的左、右焦点分别为B,C,若A为椭圆上的一点(不在x轴上),则△ABC面积的最大值是( )
A. 24 B. 12 C. 6 D. 3
2. (2024天一中学期末)已知原点为O,椭圆C:+=1(a>b>0)与直线l:x-y+1=0交于A,B两点,线段AB的中点为M,若直线OM的斜率为-,则椭圆C的离心率为( )
A. B. C. D.
3. (多选)(2024滨州期末)如图,用一个与圆柱底面成θ角的平面截圆柱,截口曲线是一个椭圆,F1,F2为该椭圆的焦点,P为椭圆上任意一点.若圆柱的底面圆半径为1,θ=,则下列结论中正确的是( )
A. 椭圆的长轴长为4
B. 椭圆的离心率为
C. 满足∠F1PF2=90°的点P共有4个
D. PF1·PF2的最大值为8
4. (2024扬州期末)设椭圆+=1(a>b>0)的半焦距为c,直线l过F(c,0),B(0,b)两点,坐标原点到直线l的距离等于FB,则椭圆的离心率为________.
5. (2024西宁大通期末)已知点A(-2,0),B在椭圆C:+=1(a>b>0)上,F1,F2分别为椭圆C的左、右焦点.
(1) 求椭圆C的离心率;
(2) 若动点P,Q均在椭圆C上,且点P,Q在x轴的两侧,求四边形PF1QF2的周长.
3.1.2 椭圆的几何性质(3)
1. 巩固椭圆的方程及简单的几何性质.
2. 感受运用方程研究曲线几何性质的思想方法.
3. 能运用椭圆的方程和几何性质解决一些综合问题.
活动一 理解椭圆的定义及标准方程
例1 求离心率为,且椭圆上一点到两焦点的距离之和为26的椭圆的标准方程.
思考1
如何进行椭圆方程的识别?
例2 P为椭圆 +=1(a>b>0)上任意一点,F1,F2为左、右焦点,判断以PF2为直径的圆与以O为圆心,a为半径的圆的位置关系,并说明理由.
活动二 理解椭圆的几何性质
例3 (1) 椭圆短轴上的两个三等分点与两个焦点构成一个正方形,则椭圆的离心率为________;
(2) 已知F1,F2分别为椭圆C:+=1(a>b>0)的左、右焦点,P是椭圆C上的一点,直线l:x=,且PQ⊥l,垂足为Q.若四边形PQF2F1为平行四边形,则椭圆C离心率的取值范围是________.
思考2
椭圆的离心率的求法:
例4 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆C上的动点,直线y=x-经过椭圆的一个焦点,△PF1F2的周长为4+2.
(1) 求椭圆的标准方程;
(2) 求|+|的最小值和最大值.
活动三 利用椭圆方程及几何性质求解最值问题
例5 已知F1,F2是椭圆C:+=1的两个焦点,点M在椭圆C上,则MF1·MF2的最大值为( )
A. 13 B. 12
C. 9 D. 6
思考3
椭圆上的点与椭圆两焦点的距离的最值问题,如何求解?
例6 已知中心在原点O,焦点在x轴上的椭圆C的离心率为,A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为.
(1) 求椭圆C的方程;
(2) 已知点E(3,0),设P,Q是椭圆C上的两个动点,满足EP⊥EQ,求·的最小值.
1. (2024阜南实验中学期末)已知椭圆C:+=1(a>b>0)的离心率为,M(3,)是椭圆C上一点,F1,F2分别是两个焦点,则△MF1F2的面积为( )
A. 4 B. 8 C. 16 D. 32
2. (2024灌云一中期末)已知点A(2,1),且F是椭圆+=1的左焦点,P是椭圆上任意一点,则PF+PA的最小值是( )
A. 6 B. 5 C. 4 D. 3
3. (多选)已知椭圆E:+=1(a>b>0)的两个焦点分别为F1,F2,与y轴正半轴交于点B,下列选项给出的条件中,能够求出椭圆E的标准方程的是( )
A. △BF1F2是等腰直角三角形
B. 椭圆E的离心率为,短轴长为2
C. △BF1F2是等边三角形,且椭圆E的离心率为
D. 椭圆E的焦距为4,且点B在圆(x-c)2+y2=9上
4. (2024秦皇岛期初)已知椭圆C:+=1的上顶点为A,左焦点为F1,线段AF1的中垂线与椭圆C交于M,N两点,则△AMN的周长为________.
5. 已知A,B分别是椭圆+=1长轴的左、右端点,点P在椭圆上,直线AP的斜率为.设M是椭圆长轴AB上的一点,点M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
3.1.2 椭圆的几何性质(2)
【活动方案】
例1 由题意,得a=2c.又a-c=,
所以c=,a=2,所以b2=9.
因为椭圆的焦点在y轴上,
所以椭圆的方程为+=1.
思考1:(1) 利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
①确定焦点位置;
②设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
③根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2,e=等.
(2) 在椭圆的简单几何性质中,轴长、离心率不能确定椭圆的焦点位置,因此仅依据这些条件求所要确定的椭圆的标准方程可能有两个.
例2 (1) 若焦点在x轴上,则a=3.因为e==,所以c=,所以b2=a2-c2=9-6=3,所以椭圆的标准方程为+=1;
若焦点在y轴上,则b=3,因为e====,解得a2=27,所以椭圆的标准方程为+=1.
故所求椭圆的标准方程为+=1或+=1.
(2) 方法一:由题意知,e2=1-=,
所以=,即a2=2b2,
所以设所求椭圆的方程为+=1或+=1.
将点M(1,2)代入椭圆方程,
得+=1或+=1,
解得b2=或b2=3,
故所求椭圆的标准方程为+=1或+=1.
方法二:设所求椭圆的方程为+=k1(k1>0)或+=k2(k2>0),
将点M(1,2)代入椭圆方程,
得+=k1或+=k2,
解得k1=,k2=,
故椭圆的方程为+=或+=,即所求椭圆的标准方程为+=1或+=1.
(3) 依题意可设椭圆方程为+=1(a>b>0).
如图,由题意可知△A1FA2为等腰直角三角形,OF为斜边A1A2的中线(高),
且OF=c,A1A2=2b,
所以c=b=3,所以a2=b2+c2=18,
故所求椭圆的标准方程为+=1.
例3 由题意,得F1F2=PF2=2c,
所以PF1=2c,所以PF1+PF2=2c+2c.
又因为PF1+PF2=2a,
所以2c+2c=2a,所以=-1,
故椭圆的离心率为-1.
例4 (,1) 由题意知,c>b,所以c2>b2.又 b2=a2-c2,所以c2>a2-c2,即2c2>a2,所以e2=>.又0思考2:(1) 直接法:若已知a,c可直接利用e=求解.若已知a,b或b,c可借助于a2=b2+c2求出c或a,再代入公式e=求解.
(2) 方程法:若a,c的值不可求,则可根据条件建立a,b,c的齐次关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.
跟踪训练 (1) A 设C(x0,y0),A(0,b),B(0,-b),则+=1,故x=(b2-y),又kAC·kBC==-,故a2=4b2,c2=a2-b2=3b2,故 e=.
(2) 方法一:由题意可设PF2=m,PF1=2m,F1F2=m,故离心率e=====.
方法二:设点P的坐标为(x,y).由PF2⊥F1F2可知点P的横坐标为c,将x=c代入椭圆方程可得y=±,所以PF2=.又由∠PF1F2=30°,可得F1F2=PF2,故2c=·,变形得(a2-c2)=2ac,等式两边同除以a2,得(1-e2)=2e,解得 e=或e=-(舍去),故椭圆C的离心率为.
例5 设椭圆的方程为+=1(a>b>0).
由题意知AC=439,BD=2 384,F2C=F2D=6 371,则a-c=OA-OF2=F2A=439+6 371=6 810,a+c=OB+OF2=F2B=2 384+6 371=8 755,
所以a=7 782.5≈7 783,c=972.5≈973,
所以b==≈7 722,
所以卫星运行的轨道方程是+=1.
【检测反馈】
1. B 由椭圆+=1,得c==3.又椭圆的左、右焦点分别为B,C,所以BC=2c=6.因为A为椭圆上的一点,设A(x0,y0),则-4≤y0≤4且y0≠0,所以S△ABC=BC·|y0|≤×6×4=12,故△ABC面积的最大值是12.
2. B 设A(x1,y1),B(x2,y2),则M(,),则两式相减,得-=,所以-=1×,即a2=4b2,即a2=4(a2-c2),3a2=4c2,故=.
3. ABC 设椭圆的长半轴长为a,短半轴长为b,半焦距为c,椭圆长轴在圆柱底面上的投影为圆柱底面圆直径,则由截面与圆柱底面成锐二面角θ=,得2a==4,故A正确;显然a=2,2b=2,解得b=1,则c==,离心率e==,故B正确;以椭圆的对称中心O为圆心,为半径作圆,由b4. 由题意易知直线l的方程为+=1,即bx+cy-bc=0,又原点到直线l的距离为,FB=,所以=,即b2+c2=2bc,解得b=c,所以b2+c2=a2=2c2,故=.
5. (1) 由点A(-2,0),B在椭圆C:+=1(a>b>0)上,
得解得则半焦距 c==1,所以椭圆C的离心率为=.
(2) 因为动点P,Q均在椭圆C上,且点P,Q在x轴的两侧,
所以由椭圆的定义,得四边形PF1QF2的周长为 PF1+PF2+QF1+QF2=4a=8.
3.1.2 椭圆的几何性质(3)
【活动方案】
例1 由题意知,2a=26,即a=13.
又e==,所以c=5,
所以b2=a2-c2=132-52=144,
当椭圆的焦点在x轴上时,椭圆的方程为+=1;
当椭圆的焦点在y轴上时,椭圆的方程为+=1,
所以椭圆的标准方程为+=1或+=1.
思考1:(1) 焦点在x轴上时,+=1(a>b>0) (参数方程,其中φ为参数);焦点在y轴上时,+=1(a>b>0) (参数方程,其中φ为参数).
+=1是椭圆,必须满足
(2) 与椭圆+=1(a>b>0)共焦点的椭圆方程可设为+=1(m>-b2).
(3) 与椭圆+=1(a>b>0)共离心率的椭圆方程可设为+=λ(λ>0).
(4) 焦点在坐标轴上,可设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
例2 如图,连接OO1,PF1,
其中O1为线段PF2的中点.
又O为F1F2的中点,所以OO1=PF1.
又PF1=2a-PF2,
所以OO1=(2a-PF2)=a-PF2,
即⊙O,⊙O1的圆心距等于两圆半径的差,
所以⊙O与⊙O1内切.
例3 (1) 由题意知c=b,即b=3c,所以a==c,所以e==.
(2) (-1,1) 设P(m,n),则Q(,n).又四边形PQF2F1为平行四边形,则m=-2c=,所以-a<思考2:(1) 直接求a,c后求e,或利用e=,求出后求e,或利用e==,求e.
(2) 将条件转化为关于a,b,c的关系式,利用b2=a2-c2消去b.等式两边同除以a2或a4构造关于(e)的方程求e.(Aa2+Bac+Cc2=0 A+Be+Ce2=0).
(3) 求离心率的取值范围时,常需根据条件或椭圆的范围建立不等式关系,通过解不等式求解,注意最后要与区间(0,1)取交集.
例4 (1) 由题意可知椭圆C的焦点在x轴上,
又直线y=x-交x轴于点(,0),
所以椭圆C的右焦点为F2(,0),
可得半焦距c=.
由△PF1F2的周长为PF1+PF2+F1F2=2a+2c,
得2a+2=4+2,解得a=2,
所以b2=a2-c2=1,
所以椭圆C的标准方程为+y2=1.
(2) 设点P(x0,y0),则+y=1,
即y=1-,-2≤x0≤2.
令坐标原点为O,则O是线段F1F2的中点,
可得|+|=|2|=2=2=,
故当x0=0时,|+|min=2;
当x0=-2或x0=2时,|+|max=4.
故|+|的最小值为2,最大值为4.
例5 C 由题意知,a2=9,即a=3,则MF1+MF2=2a=6,所以MF1·MF2≤()2=9,当且仅当MF1=MF2=3时,等号成立,所以MF1·MF2的最大值为9.
思考3:椭圆上的点与椭圆的两焦点的距离问题,常常从椭圆的定义入手,注意基本不等式的灵活运用,或记住定理:两正数,和一定,相等时积最大;积一定,相等时和最小,也可快速求解.
例6 (1) 设椭圆C的方程为+=1(a>b>0),
则解得
所以椭圆C的方程为+=1.
(2) 因为EP⊥EQ,
所以·=·(-)=||2.
设点P(x0,y0),则x+4y=36,
所以·=(x0-3)2+y=(x0-4)2+6.
又因为-6≤x0≤6,
所以当x0=4时,·取得最小值6.
【检测反馈】
1. A 由题意,得解得所以F1F2=8,S△MF1F2=F1F2·=4.
2. B 取椭圆的右焦点为M(2,0),则PF+PA=2a-PM+PA=6+PA-PM.因为|PA-PM|≤AM=1,所以-1≤PA-PM≤1,所以PF+PA=6+PA-PM∈[5,7],故PF+PA的最小值为5,当且仅当P,A,M三点共线,且点P在上半椭圆时取到最小值.
3. BD 对于A,若△BF1F2是等腰直角三角形,则c=b,没有具体数据,得不出方程,故A错误;对于B,因为椭圆E的离心率为,短轴长为2,所以=,b=1.又a2=b2+c2,所以a2=,所以椭圆E的标准方程为+y2=1,故B正确;对于C,因为△BF1F2是等边三角形,且椭圆E的离心率为,所以2c=a,b=c,没有具体数据,得不出方程,故C错误;对于D,因为椭圆E的焦距为4,点B在圆(x-c)2+y2=9上,所以c=2,b2=5.由a2=b2+c2,得a2=9,所以椭圆E的标准方程为+=1,故D正确.故选BD.
4. 8 设椭圆的右焦点为F2,如图,连接MF2,AF2,NF1.由题意,得长半轴长a=2,半焦距c=1,且AF1=AF2=F1F2=2,所以△AF1F2为等边三角形,则直线MN过点F2,所以C△AMN=AM+AN+MN=MF1+NF1+MF2+NF2=(MF1+MF2)+(NF1+NF2)=2a+2a=4a=8,即△AMN的周长为8.
5. 由题意,得直线AP的方程是x-y+6=0.
设点M的坐标是(m,0),
则点M到直线AP的距离是,
所以=|m-6|.
又-6≤m≤6,解得m=2,所以点M(2,0).
设椭圆上的点(x,y)到点M的距离为d,
则d2=(x-2)2+y2=x2-4x+4+20-x2=(x-)2+15.
因为-6≤x≤6,
所以当x=时,d取最小值,
所以椭圆上的点到点M的距离d的最小值为.
1. 熟悉椭圆的几何性质(范围,对称性,顶点,离心率).
2. 理解离心率的大小对椭圆形状的影响.
3. 通过数形结合、观察分析、归纳出椭圆的几何性质,进一步体会数形结合的思想.
活动一 掌握椭圆的几何性质
复习巩固:椭圆的定义及其标准方程:
探究:结合椭圆的标准方程+=1(a>b>0)来探究椭圆的几何性质.
1. 范围
思考1
将椭圆的标准方程进行变形,移项得=1-,你能探索出x的取值范围吗?类比能求出y的取值范围吗?
2. 对称性
思考2
在椭圆的标准方程中,将x换成-x,或将y换成-y,或同时把x,y分别换成-x,-y时,方程是否发生变化?这说明什么样的问题?
3. 顶点
思考3
根据方程写出椭圆与坐标轴的交点坐标.
结论:椭圆的顶点:
椭圆的长轴长:
椭圆的短轴长:
结合图形,思考a,b,c的几何意义分别为什么?
4. 离心率
完成下列两个实验:
(1) 将细绳的两端点固定在焦点处,用铅笔笔尖拉紧绳子,在平面上画一个椭圆,然后调整绳子的长度(分别加长、缩短),观察椭圆“扁”的程度的变化规律;
(2) 细绳的长度固定不变,将焦距分别增大或缩小,观察椭圆“扁”的程度的变化规律.
思考4
圆的形状都是相同的,而有些椭圆却比较“扁”,有些椭圆比较“圆”,用什么样的量来刻画椭圆“扁”的程度?
定义:焦距与长轴长的比叫作椭圆的离心率.
探究:椭圆的离心率的取值范围是什么?
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程 +=1(a>b>0) +=1(a>b>0)
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0),B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),B1(-b,0),B2(b,0)
轴长 长轴长=2a,短轴长=2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 F1F2=2c
对称性 对称轴:x轴和y轴,对称中心:(0,0)
离心率 e=(0
(1) 求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2) 写出椭圆C2的方程,并研究其几何性质.
活动二 掌握椭圆的几何性质的简单应用
例2 已知椭圆的中心在原点,它在x轴上的一个焦点F与短轴的两个端点B1,B2的连线互相垂直,且这个焦点与较近的长轴的端点A的距离为-,求这个椭圆的方程.
1. (2024通州、启东、如东等地期末)若椭圆+=1(a>)的离心率为,则a的值为( )
A. 2 B. 2 C. 2 D. 4
2. (2025广东东莞期末)已知边长为2的正方形的四个顶点恰好是椭圆的左、右焦点和短轴两个端点,则椭圆的标准方程为( )
A. +=1 B. +y2=1 C. +=1 D. +=1
3. (多选)若椭圆C:+=1的一个焦点坐标为(0,1),则下列结论中正确的是( )
A. m=2 B. 椭圆C的长轴长为
C. 椭圆C的短轴长为2 D. 椭圆C的离心率为
4. (2024南通中学月考)已知P为椭圆C:+y2=1上一点,A(1,0),则PA的最小值为________.
5. 求适合下列条件的椭圆的标准方程:
(1) 长轴长为6,离心率为;
(2) 经过点P(3,0),离心率为,焦点在x轴上.
3.1.2 椭圆的几何性质 (2)
1. 巩固椭圆简单的几何性质.
2. 能运用椭圆的方程和几何性质处理一些简单的实际问题.
活动一 利用椭圆的性质求椭圆方程
例1 已知椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一个正三角形,焦点在y轴上,且a-c=,求椭圆的方程.
思考1
利用椭圆的几何性质求标准方程的思路是什么?
例2 求适合下列条件的椭圆的标准方程:
(1) 椭圆过点(3,0),离心率e=;
(2) 经过点M(1,2),且与椭圆+=1有相同的离心率;
(3) 在x轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为6.
活动二 理解椭圆的离心率
例3 设椭圆的两个焦点分别为F1,F2,过点F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,求椭圆的离心率.
例4 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,椭圆C上存在点P,使∠F1PF2为钝角,则椭圆C离心率的取值范围是________.
思考2
求椭圆离心率及范围的方法有哪些?
(1) 已知椭圆E:+=1(a>b>0)的短轴的两个端点分别为A,B,C为椭圆上异于A,B的一点,直线AC与直线BC的斜率之积为-,则椭圆的离心率为( )
A. B. C. D.
(2) 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆C上的一点,PF2⊥F1F2,∠PF1F2=30°,则椭圆C的离心率为________.
活动三 掌握椭圆的几何性质在实际问题中的应用
例5 如图,我国发射的第一颗人造地球卫星的运行轨道是以地球的中心(简称“地心”)F2为一个焦点的椭圆.已知它的近地点A(长轴端点中离地面最近的点)距地面439 km, 远地点B(长轴端点中离地面最远的点)距地面2 384 km,AB是椭圆的长轴,地球的半径约为6371 km.求卫星运行的轨道方程.(精确到1 km)
解决实际问题时,首先要建立适当的平面直角坐标系,然后利用椭圆的几何性质求椭圆的标准方程,通常采用待定系数法,其步骤是:
(1) 建系;
(2) 确定焦点位置;
(3) 设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(4) 根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
1. 已知椭圆+=1的左、右焦点分别为B,C,若A为椭圆上的一点(不在x轴上),则△ABC面积的最大值是( )
A. 24 B. 12 C. 6 D. 3
2. (2024天一中学期末)已知原点为O,椭圆C:+=1(a>b>0)与直线l:x-y+1=0交于A,B两点,线段AB的中点为M,若直线OM的斜率为-,则椭圆C的离心率为( )
A. B. C. D.
3. (多选)(2024滨州期末)如图,用一个与圆柱底面成θ角的平面截圆柱,截口曲线是一个椭圆,F1,F2为该椭圆的焦点,P为椭圆上任意一点.若圆柱的底面圆半径为1,θ=,则下列结论中正确的是( )
A. 椭圆的长轴长为4
B. 椭圆的离心率为
C. 满足∠F1PF2=90°的点P共有4个
D. PF1·PF2的最大值为8
4. (2024扬州期末)设椭圆+=1(a>b>0)的半焦距为c,直线l过F(c,0),B(0,b)两点,坐标原点到直线l的距离等于FB,则椭圆的离心率为________.
5. (2024西宁大通期末)已知点A(-2,0),B在椭圆C:+=1(a>b>0)上,F1,F2分别为椭圆C的左、右焦点.
(1) 求椭圆C的离心率;
(2) 若动点P,Q均在椭圆C上,且点P,Q在x轴的两侧,求四边形PF1QF2的周长.
3.1.2 椭圆的几何性质(3)
1. 巩固椭圆的方程及简单的几何性质.
2. 感受运用方程研究曲线几何性质的思想方法.
3. 能运用椭圆的方程和几何性质解决一些综合问题.
活动一 理解椭圆的定义及标准方程
例1 求离心率为,且椭圆上一点到两焦点的距离之和为26的椭圆的标准方程.
思考1
如何进行椭圆方程的识别?
例2 P为椭圆 +=1(a>b>0)上任意一点,F1,F2为左、右焦点,判断以PF2为直径的圆与以O为圆心,a为半径的圆的位置关系,并说明理由.
活动二 理解椭圆的几何性质
例3 (1) 椭圆短轴上的两个三等分点与两个焦点构成一个正方形,则椭圆的离心率为________;
(2) 已知F1,F2分别为椭圆C:+=1(a>b>0)的左、右焦点,P是椭圆C上的一点,直线l:x=,且PQ⊥l,垂足为Q.若四边形PQF2F1为平行四边形,则椭圆C离心率的取值范围是________.
思考2
椭圆的离心率的求法:
例4 设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆C上的动点,直线y=x-经过椭圆的一个焦点,△PF1F2的周长为4+2.
(1) 求椭圆的标准方程;
(2) 求|+|的最小值和最大值.
活动三 利用椭圆方程及几何性质求解最值问题
例5 已知F1,F2是椭圆C:+=1的两个焦点,点M在椭圆C上,则MF1·MF2的最大值为( )
A. 13 B. 12
C. 9 D. 6
思考3
椭圆上的点与椭圆两焦点的距离的最值问题,如何求解?
例6 已知中心在原点O,焦点在x轴上的椭圆C的离心率为,A,B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为.
(1) 求椭圆C的方程;
(2) 已知点E(3,0),设P,Q是椭圆C上的两个动点,满足EP⊥EQ,求·的最小值.
1. (2024阜南实验中学期末)已知椭圆C:+=1(a>b>0)的离心率为,M(3,)是椭圆C上一点,F1,F2分别是两个焦点,则△MF1F2的面积为( )
A. 4 B. 8 C. 16 D. 32
2. (2024灌云一中期末)已知点A(2,1),且F是椭圆+=1的左焦点,P是椭圆上任意一点,则PF+PA的最小值是( )
A. 6 B. 5 C. 4 D. 3
3. (多选)已知椭圆E:+=1(a>b>0)的两个焦点分别为F1,F2,与y轴正半轴交于点B,下列选项给出的条件中,能够求出椭圆E的标准方程的是( )
A. △BF1F2是等腰直角三角形
B. 椭圆E的离心率为,短轴长为2
C. △BF1F2是等边三角形,且椭圆E的离心率为
D. 椭圆E的焦距为4,且点B在圆(x-c)2+y2=9上
4. (2024秦皇岛期初)已知椭圆C:+=1的上顶点为A,左焦点为F1,线段AF1的中垂线与椭圆C交于M,N两点,则△AMN的周长为________.
5. 已知A,B分别是椭圆+=1长轴的左、右端点,点P在椭圆上,直线AP的斜率为.设M是椭圆长轴AB上的一点,点M到直线AP的距离等于MB,求椭圆上的点到点M的距离d的最小值.
3.1.2 椭圆的几何性质(2)
【活动方案】
例1 由题意,得a=2c.又a-c=,
所以c=,a=2,所以b2=9.
因为椭圆的焦点在y轴上,
所以椭圆的方程为+=1.
思考1:(1) 利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
①确定焦点位置;
②设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
③根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2,e=等.
(2) 在椭圆的简单几何性质中,轴长、离心率不能确定椭圆的焦点位置,因此仅依据这些条件求所要确定的椭圆的标准方程可能有两个.
例2 (1) 若焦点在x轴上,则a=3.因为e==,所以c=,所以b2=a2-c2=9-6=3,所以椭圆的标准方程为+=1;
若焦点在y轴上,则b=3,因为e====,解得a2=27,所以椭圆的标准方程为+=1.
故所求椭圆的标准方程为+=1或+=1.
(2) 方法一:由题意知,e2=1-=,
所以=,即a2=2b2,
所以设所求椭圆的方程为+=1或+=1.
将点M(1,2)代入椭圆方程,
得+=1或+=1,
解得b2=或b2=3,
故所求椭圆的标准方程为+=1或+=1.
方法二:设所求椭圆的方程为+=k1(k1>0)或+=k2(k2>0),
将点M(1,2)代入椭圆方程,
得+=k1或+=k2,
解得k1=,k2=,
故椭圆的方程为+=或+=,即所求椭圆的标准方程为+=1或+=1.
(3) 依题意可设椭圆方程为+=1(a>b>0).
如图,由题意可知△A1FA2为等腰直角三角形,OF为斜边A1A2的中线(高),
且OF=c,A1A2=2b,
所以c=b=3,所以a2=b2+c2=18,
故所求椭圆的标准方程为+=1.
例3 由题意,得F1F2=PF2=2c,
所以PF1=2c,所以PF1+PF2=2c+2c.
又因为PF1+PF2=2a,
所以2c+2c=2a,所以=-1,
故椭圆的离心率为-1.
例4 (,1) 由题意知,c>b,所以c2>b2.又 b2=a2-c2,所以c2>a2-c2,即2c2>a2,所以e2=>.又0
(2) 方程法:若a,c的值不可求,则可根据条件建立a,b,c的齐次关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.
跟踪训练 (1) A 设C(x0,y0),A(0,b),B(0,-b),则+=1,故x=(b2-y),又kAC·kBC==-,故a2=4b2,c2=a2-b2=3b2,故 e=.
(2) 方法一:由题意可设PF2=m,PF1=2m,F1F2=m,故离心率e=====.
方法二:设点P的坐标为(x,y).由PF2⊥F1F2可知点P的横坐标为c,将x=c代入椭圆方程可得y=±,所以PF2=.又由∠PF1F2=30°,可得F1F2=PF2,故2c=·,变形得(a2-c2)=2ac,等式两边同除以a2,得(1-e2)=2e,解得 e=或e=-(舍去),故椭圆C的离心率为.
例5 设椭圆的方程为+=1(a>b>0).
由题意知AC=439,BD=2 384,F2C=F2D=6 371,则a-c=OA-OF2=F2A=439+6 371=6 810,a+c=OB+OF2=F2B=2 384+6 371=8 755,
所以a=7 782.5≈7 783,c=972.5≈973,
所以b==≈7 722,
所以卫星运行的轨道方程是+=1.
【检测反馈】
1. B 由椭圆+=1,得c==3.又椭圆的左、右焦点分别为B,C,所以BC=2c=6.因为A为椭圆上的一点,设A(x0,y0),则-4≤y0≤4且y0≠0,所以S△ABC=BC·|y0|≤×6×4=12,故△ABC面积的最大值是12.
2. B 设A(x1,y1),B(x2,y2),则M(,),则两式相减,得-=,所以-=1×,即a2=4b2,即a2=4(a2-c2),3a2=4c2,故=.
3. ABC 设椭圆的长半轴长为a,短半轴长为b,半焦距为c,椭圆长轴在圆柱底面上的投影为圆柱底面圆直径,则由截面与圆柱底面成锐二面角θ=,得2a==4,故A正确;显然a=2,2b=2,解得b=1,则c==,离心率e==,故B正确;以椭圆的对称中心O为圆心,为半径作圆,由b
5. (1) 由点A(-2,0),B在椭圆C:+=1(a>b>0)上,
得解得则半焦距 c==1,所以椭圆C的离心率为=.
(2) 因为动点P,Q均在椭圆C上,且点P,Q在x轴的两侧,
所以由椭圆的定义,得四边形PF1QF2的周长为 PF1+PF2+QF1+QF2=4a=8.
3.1.2 椭圆的几何性质(3)
【活动方案】
例1 由题意知,2a=26,即a=13.
又e==,所以c=5,
所以b2=a2-c2=132-52=144,
当椭圆的焦点在x轴上时,椭圆的方程为+=1;
当椭圆的焦点在y轴上时,椭圆的方程为+=1,
所以椭圆的标准方程为+=1或+=1.
思考1:(1) 焦点在x轴上时,+=1(a>b>0) (参数方程,其中φ为参数);焦点在y轴上时,+=1(a>b>0) (参数方程,其中φ为参数).
+=1是椭圆,必须满足
(2) 与椭圆+=1(a>b>0)共焦点的椭圆方程可设为+=1(m>-b2).
(3) 与椭圆+=1(a>b>0)共离心率的椭圆方程可设为+=λ(λ>0).
(4) 焦点在坐标轴上,可设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
例2 如图,连接OO1,PF1,
其中O1为线段PF2的中点.
又O为F1F2的中点,所以OO1=PF1.
又PF1=2a-PF2,
所以OO1=(2a-PF2)=a-PF2,
即⊙O,⊙O1的圆心距等于两圆半径的差,
所以⊙O与⊙O1内切.
例3 (1) 由题意知c=b,即b=3c,所以a==c,所以e==.
(2) (-1,1) 设P(m,n),则Q(,n).又四边形PQF2F1为平行四边形,则m=-2c=,所以-a<
(2) 将条件转化为关于a,b,c的关系式,利用b2=a2-c2消去b.等式两边同除以a2或a4构造关于(e)的方程求e.(Aa2+Bac+Cc2=0 A+Be+Ce2=0).
(3) 求离心率的取值范围时,常需根据条件或椭圆的范围建立不等式关系,通过解不等式求解,注意最后要与区间(0,1)取交集.
例4 (1) 由题意可知椭圆C的焦点在x轴上,
又直线y=x-交x轴于点(,0),
所以椭圆C的右焦点为F2(,0),
可得半焦距c=.
由△PF1F2的周长为PF1+PF2+F1F2=2a+2c,
得2a+2=4+2,解得a=2,
所以b2=a2-c2=1,
所以椭圆C的标准方程为+y2=1.
(2) 设点P(x0,y0),则+y=1,
即y=1-,-2≤x0≤2.
令坐标原点为O,则O是线段F1F2的中点,
可得|+|=|2|=2=2=,
故当x0=0时,|+|min=2;
当x0=-2或x0=2时,|+|max=4.
故|+|的最小值为2,最大值为4.
例5 C 由题意知,a2=9,即a=3,则MF1+MF2=2a=6,所以MF1·MF2≤()2=9,当且仅当MF1=MF2=3时,等号成立,所以MF1·MF2的最大值为9.
思考3:椭圆上的点与椭圆的两焦点的距离问题,常常从椭圆的定义入手,注意基本不等式的灵活运用,或记住定理:两正数,和一定,相等时积最大;积一定,相等时和最小,也可快速求解.
例6 (1) 设椭圆C的方程为+=1(a>b>0),
则解得
所以椭圆C的方程为+=1.
(2) 因为EP⊥EQ,
所以·=·(-)=||2.
设点P(x0,y0),则x+4y=36,
所以·=(x0-3)2+y=(x0-4)2+6.
又因为-6≤x0≤6,
所以当x0=4时,·取得最小值6.
【检测反馈】
1. A 由题意,得解得所以F1F2=8,S△MF1F2=F1F2·=4.
2. B 取椭圆的右焦点为M(2,0),则PF+PA=2a-PM+PA=6+PA-PM.因为|PA-PM|≤AM=1,所以-1≤PA-PM≤1,所以PF+PA=6+PA-PM∈[5,7],故PF+PA的最小值为5,当且仅当P,A,M三点共线,且点P在上半椭圆时取到最小值.
3. BD 对于A,若△BF1F2是等腰直角三角形,则c=b,没有具体数据,得不出方程,故A错误;对于B,因为椭圆E的离心率为,短轴长为2,所以=,b=1.又a2=b2+c2,所以a2=,所以椭圆E的标准方程为+y2=1,故B正确;对于C,因为△BF1F2是等边三角形,且椭圆E的离心率为,所以2c=a,b=c,没有具体数据,得不出方程,故C错误;对于D,因为椭圆E的焦距为4,点B在圆(x-c)2+y2=9上,所以c=2,b2=5.由a2=b2+c2,得a2=9,所以椭圆E的标准方程为+=1,故D正确.故选BD.
4. 8 设椭圆的右焦点为F2,如图,连接MF2,AF2,NF1.由题意,得长半轴长a=2,半焦距c=1,且AF1=AF2=F1F2=2,所以△AF1F2为等边三角形,则直线MN过点F2,所以C△AMN=AM+AN+MN=MF1+NF1+MF2+NF2=(MF1+MF2)+(NF1+NF2)=2a+2a=4a=8,即△AMN的周长为8.
5. 由题意,得直线AP的方程是x-y+6=0.
设点M的坐标是(m,0),
则点M到直线AP的距离是,
所以=|m-6|.
又-6≤m≤6,解得m=2,所以点M(2,0).
设椭圆上的点(x,y)到点M的距离为d,
则d2=(x-2)2+y2=x2-4x+4+20-x2=(x-)2+15.
因为-6≤x≤6,
所以当x=时,d取最小值,
所以椭圆上的点到点M的距离d的最小值为.
