5.1.1 平均变化率 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1
文档属性
| 名称 | 5.1.1 平均变化率 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1 |

|
|
| 格式 | docx | ||
| 文件大小 | 162.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 00:00:00 | ||
图片预览


文档简介
5.1.1 平均变化率
1. 了解平均变化率的定义, 通过平均变化率体会如何用数学模型刻画变量的变化快慢.
2. 掌握函数y=f(x)在区间[a,b]上的平均变化率.
3. 从运动的观点理解实际问题,进一步体会建立数学模型刻画客观世界“数学化”的过程.
活动一 了解平均变化率的概念
情境1:我们先来观察如图所示的气温曲线图.
思考1
从曲线图中,你能发现什么?A→B,B→C,哪一段的气温变化快?
思考2
“气温陡增”是一句生活用语,它的数学意义是什么?(从形与数两个方面给予解释情境1)
情境2:同学们都爬过山,那么平缓的山好攀登,还是陡峭的山好攀登?这是什么原因?
情境3:跑步的时候,在相同的时间内,跑得快累,还是跑得慢累?这是什么原因呢?
思考3
(1) 上述三个情境问题有什么共同点?
(2) 数学上用什么量来刻画变化的快慢?
1. 平均变化率.
思考4
结合上述问题提炼平均变化率的概念.
2. 函数的平均变化率.
思考5
试给出函数的平均变化率的概念.
解决函数平均变化率问题的关键是:
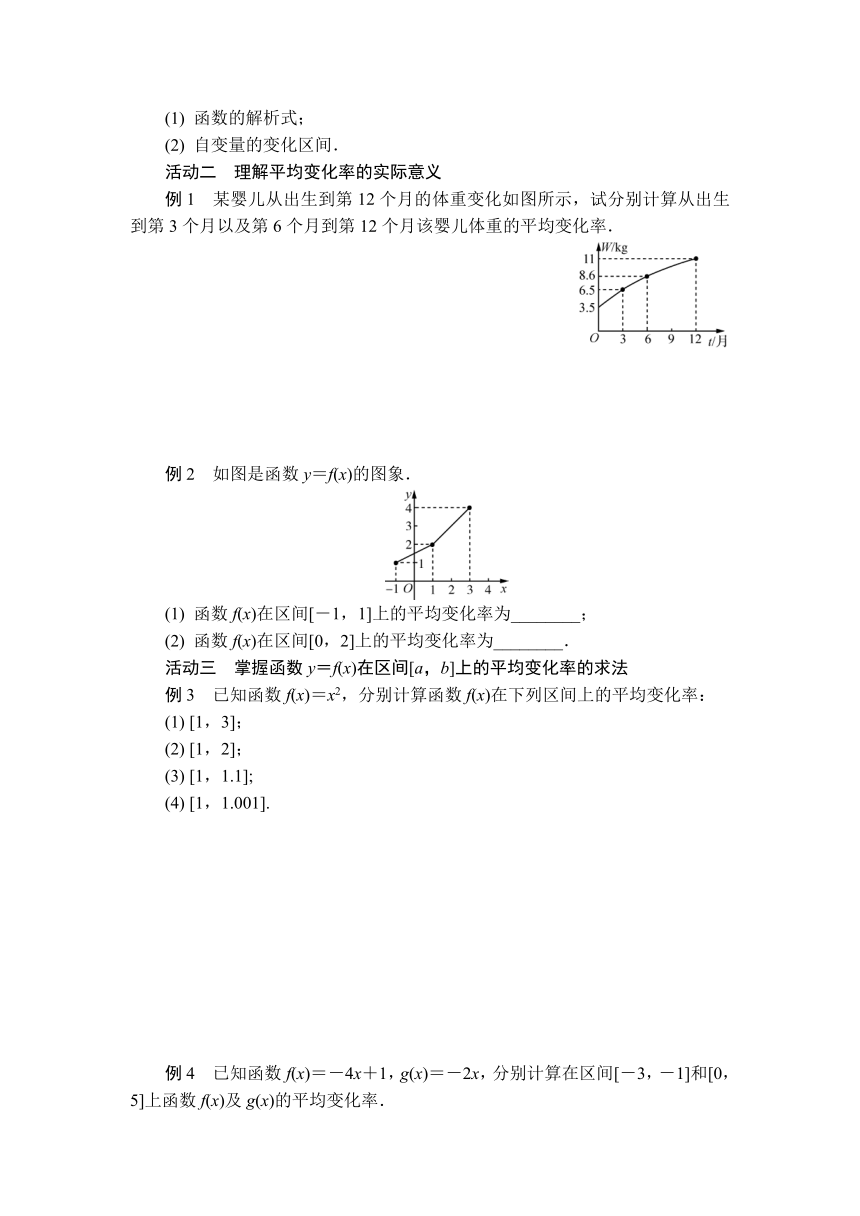
(1) 函数的解析式;
(2) 自变量的变化区间.
活动二 理解平均变化率的实际意义
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 如图是函数y=f(x)的图象.
(1) 函数f(x)在区间[-1,1]上的平均变化率为________;
(2) 函数f(x)在区间[0,2]上的平均变化率为________.
活动三 掌握函数y=f(x)在区间[a,b]上的平均变化率的求法
例3 已知函数f(x)=x2,分别计算函数f(x)在下列区间上的平均变化率:
(1) [1,3];
(2) [1,2];
(3) [1,1.1];
(4) [1,1.001].
例4 已知函数f(x)=-4x+1,g(x)=-2x,分别计算在区间[-3,-1]和[0,5]上函数f(x)及g(x)的平均变化率.
思考6
(1) 例4中若将区间改为[1,1+Δx],结果如何?
(2) 一次函数在不同区间上的平均变化率有何特征?
活动四 了解平均变化率的几何意义
例5 已知曲线f(x)=x3上的两点P(1,1)和Q(1+Δx,1+Δy),求直线PQ的斜率,并求当Δx=0.1 时直线PQ的斜率.
1. (2025北京延庆期末)函数f(x)=x2在区间[2,4]上的平均变化率等于( )
A. 2 B. 4 C. 6 D. 8
2. (2025辽宁锦州期末)降低室内微生物密度的有效方法是定时给室内注入新鲜空气,即开窗通风换气.在某室内,空气中微生物密度c(单位:mg/m3)随开窗通风换气时间t(单位:min)的关系如图所示,则下列时间段内,空气中微生物密度变化的平均速度最快的是( )
A. [5,10] B. [15,20] C. [25,30] D. [30,35]
3. (多选)设函数y=f(x),当自变量x由x0变化到x0+Δx时,下列说法中正确的是( )
A. Δx可以是正数也可以是负数,但不能为0
B. 函数值的改变量Δy=f(x0+Δx)-f(x0)
C. 函数f(x)在区间[x0,x0+Δx]上的平均变化率为f(x0)·Δx
D. 函数f(x)在区间[x0,x0+Δx]上的平均变化率为
4. 函数y=2x2-4在区间[1,1+Δx]上的平均变化率为________.
5. (2024海门中学月考)已知函数f(x)=x2+3x在区间[0,m]上的平均变化率是函数g(x)=2x+1在区间[1,4]上的平均变化率的3倍,求实数m的值.
5.1.1 平均变化率
【活动方案】
思考1:容易看出点B,C之间的曲线比点A,B之间的曲线更加“陡峭”.B→C段的气温变化快.
思考2:从形的角度:B→C段的曲线较A→B段更陡峭;从数的角度:气温在区间[1,32]上的平均变化率约为0.5;气温在区间[32,34]上的平均变化率为7.4.
情境2:平缓的山好攀登.因为山越陡峭,当爬山移动的水平距离变化量一定时,垂直距离的变化量越大,从而在陡峭的山上攀登平均变化量就越大.
情境3:跑得快累.因为当时间变化量一定时,跑得快的位移变化量就大,从而在这时间内的平均变化量就大.
思考3:(1) 都和平均变化率有关.
(2) 平均变化率.
思考4:量化两点间一段曲线的陡峭程度,并称该比值为平均变化率.
思考5:函数f(x)在区间[x1,x2]上的平均变化率为.
例1 从出生到第3个月,该婴儿体重的平均变化率为=1(kg/月),
从第6个月到第12个月,该婴儿体重的平均变化率为==0.4(kg/月).
例2 (1) 函数f(x)在区间[-1,1]上的平均变化率为==.
(2) 由函数f(x)的图象知,f(x)=所以函数f(x)在区间[0,2]上的平均变化率为==.
例3 (1) 函数f(x)在区间[1,3]上的平均变化率为=4.
(2) 函数f(x)在区间[1,2]上的平均变化率为=3.
(3) 函数f(x)在区间[1,1.1]上的平均变化率为=2.1.
(4) 函数f(x)在区间[1,1.001]上的平均变化率为=2.001.
例4 函数f(x)在区间[-3,-1]上的平均变化率为=-4;
函数f(x)在区间[0,5]上的平均变化率为=-4;
函数g(x)在区间[-3,-1]上的平均变化率为=-2;
函数g(x)在区间[0,5]上的平均变化率为=-2.
思考6:(1) 函数f(x)在区间[1,1+Δx]上的平均变化率为=-4,
函数g(x)在区间[1,1+Δx]上的平均变化率为=-2.
综上可知,结果保持不变.
(2) 一次函数在不同区间上的平均变化率等于斜率.
例5 因为Δy=f(1+Δx)-f(1)=(1+Δx)3-1=(Δx)3+3(Δx)2+3Δx,
所以直线PQ的斜率k==(Δx)2+3Δx+3.
设当Δx=0.1时,直线PQ的斜率为k1,则k1=0.12+3×0.1+3=3.31.
【检测反馈】
1. C 函数f(x)=x2在区间[2,4]上的平均变化率等于=6.
2. B 如图,分别令t=5,t=10,t=15,t=20,t=25,t=30,t=35所对应的点为A,B,C,D,E,F,G,0>kAB>kCD,0>kEF>kCD,0>kFG>kCD,所以时间[15,20]内的空气中微生物密度变化的平均速度最快.
3. ABD 由平均变化率的定义可知自变量的改变量不能为零,可以为正数或负数,函数值的改变量Δy为f(x0+Δx)-f(x0),平均变化率为函数值的改变量与自变量改变量的比值,即为,故选ABD.
4. 4+2Δx ===4+2Δx.
5. 函数g(x)在区间[1,4]上的平均变化率为==2.
函数f(x)在区间[0,m]上的平均变化率为==m+3.
由题意,得m+3=2×3,
解得m=3.
1. 了解平均变化率的定义, 通过平均变化率体会如何用数学模型刻画变量的变化快慢.
2. 掌握函数y=f(x)在区间[a,b]上的平均变化率.
3. 从运动的观点理解实际问题,进一步体会建立数学模型刻画客观世界“数学化”的过程.
活动一 了解平均变化率的概念
情境1:我们先来观察如图所示的气温曲线图.
思考1
从曲线图中,你能发现什么?A→B,B→C,哪一段的气温变化快?
思考2
“气温陡增”是一句生活用语,它的数学意义是什么?(从形与数两个方面给予解释情境1)
情境2:同学们都爬过山,那么平缓的山好攀登,还是陡峭的山好攀登?这是什么原因?
情境3:跑步的时候,在相同的时间内,跑得快累,还是跑得慢累?这是什么原因呢?
思考3
(1) 上述三个情境问题有什么共同点?
(2) 数学上用什么量来刻画变化的快慢?
1. 平均变化率.
思考4
结合上述问题提炼平均变化率的概念.
2. 函数的平均变化率.
思考5
试给出函数的平均变化率的概念.
解决函数平均变化率问题的关键是:
(1) 函数的解析式;
(2) 自变量的变化区间.
活动二 理解平均变化率的实际意义
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 如图是函数y=f(x)的图象.
(1) 函数f(x)在区间[-1,1]上的平均变化率为________;
(2) 函数f(x)在区间[0,2]上的平均变化率为________.
活动三 掌握函数y=f(x)在区间[a,b]上的平均变化率的求法
例3 已知函数f(x)=x2,分别计算函数f(x)在下列区间上的平均变化率:
(1) [1,3];
(2) [1,2];
(3) [1,1.1];
(4) [1,1.001].
例4 已知函数f(x)=-4x+1,g(x)=-2x,分别计算在区间[-3,-1]和[0,5]上函数f(x)及g(x)的平均变化率.
思考6
(1) 例4中若将区间改为[1,1+Δx],结果如何?
(2) 一次函数在不同区间上的平均变化率有何特征?
活动四 了解平均变化率的几何意义
例5 已知曲线f(x)=x3上的两点P(1,1)和Q(1+Δx,1+Δy),求直线PQ的斜率,并求当Δx=0.1 时直线PQ的斜率.
1. (2025北京延庆期末)函数f(x)=x2在区间[2,4]上的平均变化率等于( )
A. 2 B. 4 C. 6 D. 8
2. (2025辽宁锦州期末)降低室内微生物密度的有效方法是定时给室内注入新鲜空气,即开窗通风换气.在某室内,空气中微生物密度c(单位:mg/m3)随开窗通风换气时间t(单位:min)的关系如图所示,则下列时间段内,空气中微生物密度变化的平均速度最快的是( )
A. [5,10] B. [15,20] C. [25,30] D. [30,35]
3. (多选)设函数y=f(x),当自变量x由x0变化到x0+Δx时,下列说法中正确的是( )
A. Δx可以是正数也可以是负数,但不能为0
B. 函数值的改变量Δy=f(x0+Δx)-f(x0)
C. 函数f(x)在区间[x0,x0+Δx]上的平均变化率为f(x0)·Δx
D. 函数f(x)在区间[x0,x0+Δx]上的平均变化率为
4. 函数y=2x2-4在区间[1,1+Δx]上的平均变化率为________.
5. (2024海门中学月考)已知函数f(x)=x2+3x在区间[0,m]上的平均变化率是函数g(x)=2x+1在区间[1,4]上的平均变化率的3倍,求实数m的值.
5.1.1 平均变化率
【活动方案】
思考1:容易看出点B,C之间的曲线比点A,B之间的曲线更加“陡峭”.B→C段的气温变化快.
思考2:从形的角度:B→C段的曲线较A→B段更陡峭;从数的角度:气温在区间[1,32]上的平均变化率约为0.5;气温在区间[32,34]上的平均变化率为7.4.
情境2:平缓的山好攀登.因为山越陡峭,当爬山移动的水平距离变化量一定时,垂直距离的变化量越大,从而在陡峭的山上攀登平均变化量就越大.
情境3:跑得快累.因为当时间变化量一定时,跑得快的位移变化量就大,从而在这时间内的平均变化量就大.
思考3:(1) 都和平均变化率有关.
(2) 平均变化率.
思考4:量化两点间一段曲线的陡峭程度,并称该比值为平均变化率.
思考5:函数f(x)在区间[x1,x2]上的平均变化率为.
例1 从出生到第3个月,该婴儿体重的平均变化率为=1(kg/月),
从第6个月到第12个月,该婴儿体重的平均变化率为==0.4(kg/月).
例2 (1) 函数f(x)在区间[-1,1]上的平均变化率为==.
(2) 由函数f(x)的图象知,f(x)=所以函数f(x)在区间[0,2]上的平均变化率为==.
例3 (1) 函数f(x)在区间[1,3]上的平均变化率为=4.
(2) 函数f(x)在区间[1,2]上的平均变化率为=3.
(3) 函数f(x)在区间[1,1.1]上的平均变化率为=2.1.
(4) 函数f(x)在区间[1,1.001]上的平均变化率为=2.001.
例4 函数f(x)在区间[-3,-1]上的平均变化率为=-4;
函数f(x)在区间[0,5]上的平均变化率为=-4;
函数g(x)在区间[-3,-1]上的平均变化率为=-2;
函数g(x)在区间[0,5]上的平均变化率为=-2.
思考6:(1) 函数f(x)在区间[1,1+Δx]上的平均变化率为=-4,
函数g(x)在区间[1,1+Δx]上的平均变化率为=-2.
综上可知,结果保持不变.
(2) 一次函数在不同区间上的平均变化率等于斜率.
例5 因为Δy=f(1+Δx)-f(1)=(1+Δx)3-1=(Δx)3+3(Δx)2+3Δx,
所以直线PQ的斜率k==(Δx)2+3Δx+3.
设当Δx=0.1时,直线PQ的斜率为k1,则k1=0.12+3×0.1+3=3.31.
【检测反馈】
1. C 函数f(x)=x2在区间[2,4]上的平均变化率等于=6.
2. B 如图,分别令t=5,t=10,t=15,t=20,t=25,t=30,t=35所对应的点为A,B,C,D,E,F,G,0>kAB>kCD,0>kEF>kCD,0>kFG>kCD,所以时间[15,20]内的空气中微生物密度变化的平均速度最快.
3. ABD 由平均变化率的定义可知自变量的改变量不能为零,可以为正数或负数,函数值的改变量Δy为f(x0+Δx)-f(x0),平均变化率为函数值的改变量与自变量改变量的比值,即为,故选ABD.
4. 4+2Δx ===4+2Δx.
5. 函数g(x)在区间[1,4]上的平均变化率为==2.
函数f(x)在区间[0,m]上的平均变化率为==m+3.
由题意,得m+3=2×3,
解得m=3.
