第1章 直线与方程 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1
文档属性
| 名称 | 第1章 直线与方程 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1 |
|
|
| 格式 | docx | ||
| 文件大小 | 153.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 23:26:07 | ||
图片预览




文档简介
第1章 直线与方程
1. 梳理本章知识,构建知识网络.
2. 巩固直线的有关知识与思想方法.
活动一 建构知识网络
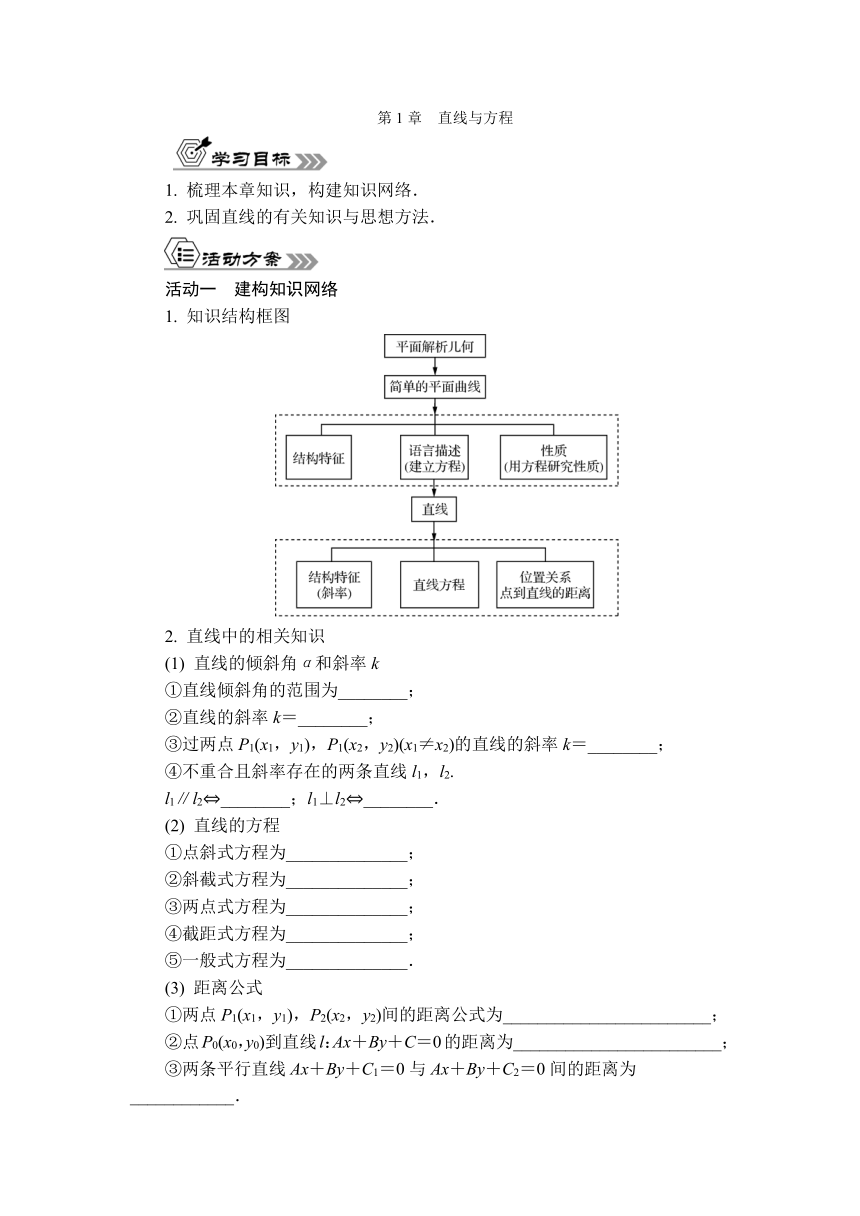
1. 知识结构框图
2. 直线中的相关知识
(1) 直线的倾斜角α和斜率k
①直线倾斜角的范围为________;
②直线的斜率k=________;
③过两点P1(x1,y1),P1(x2,y2)(x1≠x2)的直线的斜率k=________;
④不重合且斜率存在的两条直线l1,l2.
l1∥l2 ________;l1⊥l2 ________.
(2) 直线的方程
①点斜式方程为______________;
②斜截式方程为______________;
③两点式方程为______________;
④截距式方程为______________;
⑤一般式方程为______________.
(3) 距离公式
①两点P1(x1,y1),P2(x2,y2)间的距离公式为________________________;
②点P0(x0,y0)到直线l:Ax+By+C=0的距离为________________________;
③两条平行直线Ax+By+C1=0与Ax+By+C2=0间的距离为____________.
(4) 两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的位置关系
①l1与l2相交 ________________;
②l1∥l2 ________________________;
③l1⊥l2 ________________.
(5) 三种常见的对称问题
①点关于点的对称
点P(x0,y0)关于点M(a,b)的对称点为P′________;
②点关于直线的对称
若两点P1(x1,y1)与P2(x2,y2)关于直线l:Ax+By+C=0对称,则由方程组可得点P1关于直线l对称的点P2的坐标(x2,y2)(其中A≠0,x1≠x2);
③线关于点、线的对称
线是点构成的集合,直线的方程是直线上任一点P(x,y)的坐标x,y满足的表达式,故求直线关于点、线的对称,可转化为求该直线上任一点关于点、线的对称.
活动二 直线的方程
例1 在平面直角坐标系中,已知菱形ABCD的顶点A(-1,2)和C(5,4),AB所在直线的方程为x-y+3=0.
(1) 求对角线BD所在直线的方程;
(2) 求AD所在直线的方程.
例2 已知直线l1过点A(2,3),且________.
(1) 若横线上填写的是“过点B(3,-2)”,求直线l1的方程;
(2) 在①直线l1与直线l2:3x-y+1=0平行;②直线l1与直线l2:x+3y-2=0垂直;③直线l2的倾斜角为45°,且直线l1的斜率是直线l2的斜率的3倍,这三个条件中任选一个,填在横线上,求出直线l1的方程.
活动三 两直线的位置关系
例3 已知直线l1:ax+by+6=0和直线l2:(a-1)x+y+2=0,求分别满足下列条件的a,b的值.
(1) 直线l1过点(-3,0),且直线l1和l2垂直;
(2) 若直线l1和l2平行,且直线l1在y轴上的截距为-3.
例4 已知△ABC的三个顶点A(4,-6),B(-4,0),C(-1,4),求:
(1) AC边上的高BD所在直线的方程;
(2) BC的垂直平分线EF所在直线的方程.
活动四 直线的综合应用
例5 求直线a:2x+y-4=0关于直线l:3x+4y-1=0对称的直线b的方程.
例6 设直线l的方程为(2-m)x+(2m+1)y+3m+4=0.
(1) 当m为何值时,点Q(3,4)到直线l的距离最大,最大值为多少?
(2) 若直线l分别与x轴,y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
1. (2024常德一中月考)已知两点A(3,2)和B(-1,4)到直线mx+y+3=0的距离相等,则实数m的值为( )
A. -6或 B. -或1 C. -或 D. 0或
2. (2024南京五校联盟期末)斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致.一座斜拉桥共有10对拉索,在索塔两侧对称排列,已知拉索上端相邻两个锚的间距PiPi+1(i=1,2,3,…,9)均为4m,拉索下端相邻两个锚的间距AiAi+1,BiBi+1(i=1,2,3,…,9)均为16m,最短拉索P1A1满足OP1=60m,OA1=96m,若建立如图所示的平面直角坐标系,则最长拉索P10B10所在直线的斜率为( )
A. B. C. D.
3. (多选)设a为非零实数,直线l1:ax+2ay+1=0,l2:(a-1)x-(a+1)y-4=0,则下列说法中正确的是( )
A. 若l1∥l2,则a=3 B. 若l1⊥l2,则a=-3
C. 直线l1恒过点(-2,1) D. 当a∈[-1,0)∪(0,1]时,l2不经过第一象限
4. 已知直线l1:x-2y+1=0与直线l2:x-2y+4=0,在直线l1上任取一点A,在直线l2上任取一点B,连接AB,取AB的靠近点A的三等分点C,过点C作l1的平行线l3,则l1与l3间的距离为________.
5. 已知△ABC的顶点A(-5,0),B(2,-2),BC边上的高所在直线的方程为x+5y+5=0.
(1) 求直线BC的方程;
(2) 若________,求直线AC的方程.
在①点C在直线x-y=0上;②BC边上的中线所在直线的方程为x+y-12=0,这两个条件中任选一个,补充在横线上.
第1章 直线与方程
【活动方案】
活动一 略
例1 (1) 由A(-1,2)和C(5,4),得kAC==,AC的中点M(2,3).因为四边形ABCD为菱形,所以BD⊥AC,且M(2,3)为BD的中点,所以kBD=-3,所以对角线BD所在直线的方程为y-3=-3(x-2),即3x+y-9=0.
(2) 由解得点B(,),所以kBC==-.因为AD∥BC,所以kAD=-,所以直线AD的方程为y-2=-(x+1),即x+7y-13=0.
例2 (1) 依题意,得直线l1的方程为=,化简,得直线l1的方程为5x+y-13=0.
(2) 若选①:设直线l1的方程为3x-y+λ=0(λ≠1),将点A(2,3)代入上式,得3×2-3+λ=0,解得λ=-3,故直线l1的方程为3x-y-3=0.
若选②:设直线l1的方程为3x-y+λ=0,将点 A(2,3)代入上式,得3×2-3+λ=0,解得λ=-3,故直线l1的方程为3x-y-3=0.
若选③:易知直线l2的斜率k2=tan 45°=1,故直线l1的斜率k1=3k2=3,故直线l1的方程为y-3=3(x-2),即3x-y-3=0.
例3 (1) 因为直线l1和l2垂直,
所以a×(a-1)+b×1=0.
又直线l1过点(-3,0),
故-3a+6=0,联立两式,解得a=2,b=-2.
故有a=2,b=-2.
(2) 因为直线l1和l2平行,
所以
又直线l1在y轴上的截距为-3,故
联立解得a=2,b=2,
故有a=2,b=2.
例4 (1) 由斜率公式易知kAC=-2,
所以直线BD的斜率k=.
又直线BD过点B(-4,0),代入点斜式,得
直线BD的方程为x-2y+4=0.
(2) 因为kBC=,所以kEF=-.
又线段BC的中点为(-,2),
所以EF所在直线的方程为y-2=-(x+),
整理,得所求的直线方程为6x+8y-1=0.
例5 在直线a:2x+y-4=0上取一点A(2,0),设点A关于直线l的对称点为B(x0,y0),
则
解得点B(,-).
由解得交点D(3,-2).
由两点式方程,得直线b的方程为2x+11y+16=0.
例6 (1) 根据题意,得直线l过定点P(-1,-2),
则由点Q(3,4)到直线的距离最大,
可知点Q与定点P(-1,-2)的连线的距离就是所求最大值,
即=2为最大值.
因为kPQ==,
所以直线(2-m)x+(2m+1)y+3m+4=0的斜率为-,即-=-,解得m=.
(2) 若直线分别与x轴,y轴的负半轴交于A,B两点,直线l方程为y+2=k(x+1),k<0,则点A(-1,0),B(0,k-2),
S△AOB=|-1|·|k-2|=(-1)(k-2)=2+(+)≥2+2=4,当且仅当k=-2时取等号,
所以△AOB面积的最小值为4,
此时直线l的方程为2x+y+4=0.
【检测反馈】
1. A 由题意,得=,即|3m+5|=|7-m|,解得m=-6或m=.
2. D 由题意,得OA10=OA1+A1A10=96+9×16=240m,OP10=OP1+P1P10=60+9×4=96(m),故B10(-240,0),P10(0,96),则kP10B10==.
3. BD 若l1∥l2,则=≠,解得a=或a=0(舍去),故A错误;若l1⊥l2,则 a(a-1)-2a(a+1)=0,解得a=-3或a=0(舍去),故B正确;将点(-2,1)代入直线l1:ax+2ay+1=0,得-2a+2a+1≠0,故直线l1不过点(-2,1),故C错误;若直线l2不经过第一象限,当-(a+1)≠0且a-1≠0时,l2:y=x-,则解得-14. 过点A作AD⊥l2于点D,交l3于点E,如图所示.因为l1∥l2∥l3,且由题意得=,所以Rt△ABD∽Rt△ACE,所以==.又直线l1与直线l2间的距离AD==,所以l1与l3间的距离为AE=AD=.
5. (1) 因为点B(2,-2),BC边上的高所在直线的方程为x+5y+5=0,
所以直线BC的斜率k=5,
故所求的直线方程为y+2=5(x-2),
即5x-y-12=0.
(2) 若选①点C在直线x-y=0上,
由得x=y=3,即点C(3,3).
此时kAC=,则AC所在的直线方程为y=(x+5),即3x-8y+15=0.
若选②BC边上的中线所在直线的方程为x+y-12=0,
由解得
即BC的中点坐标为(4,8).
设点C(x,y),则2+x=8,-2+y=16,
所以x=6,y=18,
所以kAC=,则AC所在的直线方程为y=(x+5),即18x-11y+90=0.
1. 梳理本章知识,构建知识网络.
2. 巩固直线的有关知识与思想方法.
活动一 建构知识网络
1. 知识结构框图
2. 直线中的相关知识
(1) 直线的倾斜角α和斜率k
①直线倾斜角的范围为________;
②直线的斜率k=________;
③过两点P1(x1,y1),P1(x2,y2)(x1≠x2)的直线的斜率k=________;
④不重合且斜率存在的两条直线l1,l2.
l1∥l2 ________;l1⊥l2 ________.
(2) 直线的方程
①点斜式方程为______________;
②斜截式方程为______________;
③两点式方程为______________;
④截距式方程为______________;
⑤一般式方程为______________.
(3) 距离公式
①两点P1(x1,y1),P2(x2,y2)间的距离公式为________________________;
②点P0(x0,y0)到直线l:Ax+By+C=0的距离为________________________;
③两条平行直线Ax+By+C1=0与Ax+By+C2=0间的距离为____________.
(4) 两条直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的位置关系
①l1与l2相交 ________________;
②l1∥l2 ________________________;
③l1⊥l2 ________________.
(5) 三种常见的对称问题
①点关于点的对称
点P(x0,y0)关于点M(a,b)的对称点为P′________;
②点关于直线的对称
若两点P1(x1,y1)与P2(x2,y2)关于直线l:Ax+By+C=0对称,则由方程组可得点P1关于直线l对称的点P2的坐标(x2,y2)(其中A≠0,x1≠x2);
③线关于点、线的对称
线是点构成的集合,直线的方程是直线上任一点P(x,y)的坐标x,y满足的表达式,故求直线关于点、线的对称,可转化为求该直线上任一点关于点、线的对称.
活动二 直线的方程
例1 在平面直角坐标系中,已知菱形ABCD的顶点A(-1,2)和C(5,4),AB所在直线的方程为x-y+3=0.
(1) 求对角线BD所在直线的方程;
(2) 求AD所在直线的方程.
例2 已知直线l1过点A(2,3),且________.
(1) 若横线上填写的是“过点B(3,-2)”,求直线l1的方程;
(2) 在①直线l1与直线l2:3x-y+1=0平行;②直线l1与直线l2:x+3y-2=0垂直;③直线l2的倾斜角为45°,且直线l1的斜率是直线l2的斜率的3倍,这三个条件中任选一个,填在横线上,求出直线l1的方程.
活动三 两直线的位置关系
例3 已知直线l1:ax+by+6=0和直线l2:(a-1)x+y+2=0,求分别满足下列条件的a,b的值.
(1) 直线l1过点(-3,0),且直线l1和l2垂直;
(2) 若直线l1和l2平行,且直线l1在y轴上的截距为-3.
例4 已知△ABC的三个顶点A(4,-6),B(-4,0),C(-1,4),求:
(1) AC边上的高BD所在直线的方程;
(2) BC的垂直平分线EF所在直线的方程.
活动四 直线的综合应用
例5 求直线a:2x+y-4=0关于直线l:3x+4y-1=0对称的直线b的方程.
例6 设直线l的方程为(2-m)x+(2m+1)y+3m+4=0.
(1) 当m为何值时,点Q(3,4)到直线l的距离最大,最大值为多少?
(2) 若直线l分别与x轴,y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
1. (2024常德一中月考)已知两点A(3,2)和B(-1,4)到直线mx+y+3=0的距离相等,则实数m的值为( )
A. -6或 B. -或1 C. -或 D. 0或
2. (2024南京五校联盟期末)斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致.一座斜拉桥共有10对拉索,在索塔两侧对称排列,已知拉索上端相邻两个锚的间距PiPi+1(i=1,2,3,…,9)均为4m,拉索下端相邻两个锚的间距AiAi+1,BiBi+1(i=1,2,3,…,9)均为16m,最短拉索P1A1满足OP1=60m,OA1=96m,若建立如图所示的平面直角坐标系,则最长拉索P10B10所在直线的斜率为( )
A. B. C. D.
3. (多选)设a为非零实数,直线l1:ax+2ay+1=0,l2:(a-1)x-(a+1)y-4=0,则下列说法中正确的是( )
A. 若l1∥l2,则a=3 B. 若l1⊥l2,则a=-3
C. 直线l1恒过点(-2,1) D. 当a∈[-1,0)∪(0,1]时,l2不经过第一象限
4. 已知直线l1:x-2y+1=0与直线l2:x-2y+4=0,在直线l1上任取一点A,在直线l2上任取一点B,连接AB,取AB的靠近点A的三等分点C,过点C作l1的平行线l3,则l1与l3间的距离为________.
5. 已知△ABC的顶点A(-5,0),B(2,-2),BC边上的高所在直线的方程为x+5y+5=0.
(1) 求直线BC的方程;
(2) 若________,求直线AC的方程.
在①点C在直线x-y=0上;②BC边上的中线所在直线的方程为x+y-12=0,这两个条件中任选一个,补充在横线上.
第1章 直线与方程
【活动方案】
活动一 略
例1 (1) 由A(-1,2)和C(5,4),得kAC==,AC的中点M(2,3).因为四边形ABCD为菱形,所以BD⊥AC,且M(2,3)为BD的中点,所以kBD=-3,所以对角线BD所在直线的方程为y-3=-3(x-2),即3x+y-9=0.
(2) 由解得点B(,),所以kBC==-.因为AD∥BC,所以kAD=-,所以直线AD的方程为y-2=-(x+1),即x+7y-13=0.
例2 (1) 依题意,得直线l1的方程为=,化简,得直线l1的方程为5x+y-13=0.
(2) 若选①:设直线l1的方程为3x-y+λ=0(λ≠1),将点A(2,3)代入上式,得3×2-3+λ=0,解得λ=-3,故直线l1的方程为3x-y-3=0.
若选②:设直线l1的方程为3x-y+λ=0,将点 A(2,3)代入上式,得3×2-3+λ=0,解得λ=-3,故直线l1的方程为3x-y-3=0.
若选③:易知直线l2的斜率k2=tan 45°=1,故直线l1的斜率k1=3k2=3,故直线l1的方程为y-3=3(x-2),即3x-y-3=0.
例3 (1) 因为直线l1和l2垂直,
所以a×(a-1)+b×1=0.
又直线l1过点(-3,0),
故-3a+6=0,联立两式,解得a=2,b=-2.
故有a=2,b=-2.
(2) 因为直线l1和l2平行,
所以
又直线l1在y轴上的截距为-3,故
联立解得a=2,b=2,
故有a=2,b=2.
例4 (1) 由斜率公式易知kAC=-2,
所以直线BD的斜率k=.
又直线BD过点B(-4,0),代入点斜式,得
直线BD的方程为x-2y+4=0.
(2) 因为kBC=,所以kEF=-.
又线段BC的中点为(-,2),
所以EF所在直线的方程为y-2=-(x+),
整理,得所求的直线方程为6x+8y-1=0.
例5 在直线a:2x+y-4=0上取一点A(2,0),设点A关于直线l的对称点为B(x0,y0),
则
解得点B(,-).
由解得交点D(3,-2).
由两点式方程,得直线b的方程为2x+11y+16=0.
例6 (1) 根据题意,得直线l过定点P(-1,-2),
则由点Q(3,4)到直线的距离最大,
可知点Q与定点P(-1,-2)的连线的距离就是所求最大值,
即=2为最大值.
因为kPQ==,
所以直线(2-m)x+(2m+1)y+3m+4=0的斜率为-,即-=-,解得m=.
(2) 若直线分别与x轴,y轴的负半轴交于A,B两点,直线l方程为y+2=k(x+1),k<0,则点A(-1,0),B(0,k-2),
S△AOB=|-1|·|k-2|=(-1)(k-2)=2+(+)≥2+2=4,当且仅当k=-2时取等号,
所以△AOB面积的最小值为4,
此时直线l的方程为2x+y+4=0.
【检测反馈】
1. A 由题意,得=,即|3m+5|=|7-m|,解得m=-6或m=.
2. D 由题意,得OA10=OA1+A1A10=96+9×16=240m,OP10=OP1+P1P10=60+9×4=96(m),故B10(-240,0),P10(0,96),则kP10B10==.
3. BD 若l1∥l2,则=≠,解得a=或a=0(舍去),故A错误;若l1⊥l2,则 a(a-1)-2a(a+1)=0,解得a=-3或a=0(舍去),故B正确;将点(-2,1)代入直线l1:ax+2ay+1=0,得-2a+2a+1≠0,故直线l1不过点(-2,1),故C错误;若直线l2不经过第一象限,当-(a+1)≠0且a-1≠0时,l2:y=x-,则解得-1
5. (1) 因为点B(2,-2),BC边上的高所在直线的方程为x+5y+5=0,
所以直线BC的斜率k=5,
故所求的直线方程为y+2=5(x-2),
即5x-y-12=0.
(2) 若选①点C在直线x-y=0上,
由得x=y=3,即点C(3,3).
此时kAC=,则AC所在的直线方程为y=(x+5),即3x-8y+15=0.
若选②BC边上的中线所在直线的方程为x+y-12=0,
由解得
即BC的中点坐标为(4,8).
设点C(x,y),则2+x=8,-2+y=16,
所以x=6,y=18,
所以kAC=,则AC所在的直线方程为y=(x+5),即18x-11y+90=0.
