第3章 圆锥曲线与方程 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1
文档属性
| 名称 | 第3章 圆锥曲线与方程 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修1 | 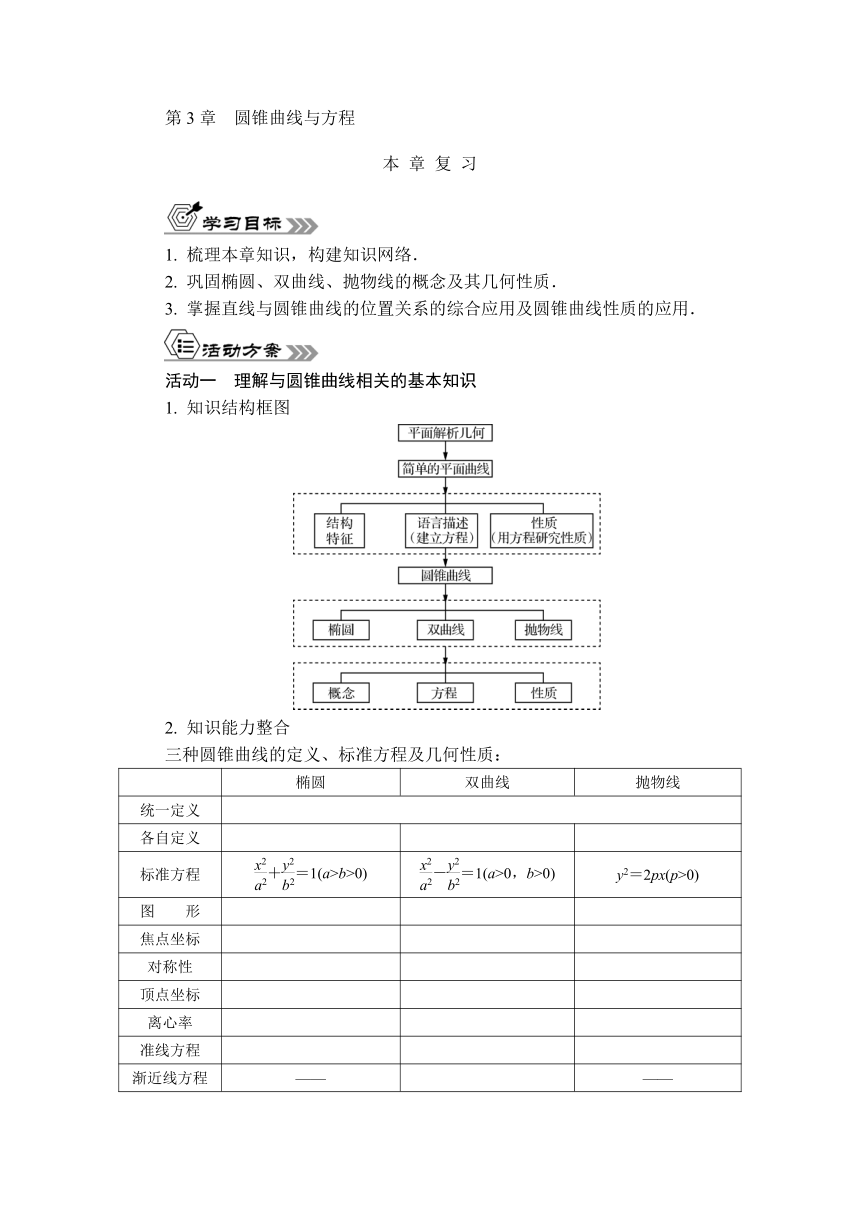 | |
| 格式 | docx | ||
| 文件大小 | 225.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 23:27:05 | ||
图片预览





文档简介
第3章 圆锥曲线与方程
本 章 复 习
1. 梳理本章知识,构建知识网络.
2. 巩固椭圆、双曲线、抛物线的概念及其几何性质.
3. 掌握直线与圆锥曲线的位置关系的综合应用及圆锥曲线性质的应用.
活动一 理解与圆锥曲线相关的基本知识
1. 知识结构框图
2. 知识能力整合
三种圆锥曲线的定义、标准方程及几何性质:
椭圆 双曲线 抛物线
统一定义
各自定义
标准方程 +=1(a>b>0) -=1(a>0,b>0) y2=2px(p>0)
图 形
焦点坐标
对称性
顶点坐标
离心率
准线方程
渐近线方程 —— ——
活动二 圆锥曲线的方程与性质
例1 已知点P(x,y)到定点F(0,)的距离与它到定直线l:y=的距离的比是常数,点P 的轨迹为曲线E.
(1) 求曲线E的方程;
(2) 设点Q(m,0)(m>1),若PQ的最大值为,求实数m的值.
根据条件先判断动点的轨迹,再求其轨迹方程.
在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(-1,0)和F2(1,0),M为BC边的中点.
(1) 求点M的轨迹方程;
(2) 设点M的轨迹为曲线Γ,直线MF1与曲线Γ的另一个交点为N,线段MF2的中点为E,记 S=S△NF1O+S△MF1E,求S的最大值.
例2 (2024苏州调研)如图,已知点B(2,-1),BC⊥x轴于点C,M是线段OB上任意一点,MD⊥x轴于点D,ME⊥BC于点E,OE与MD相交于点P,则点P的轨迹方程为( )
A. y2=x(0≤x≤2)
B. y2=x(0≤x≤2)
C. x2=-y(0≤x≤2)
D. x2=-4y(0≤x≤2)
消参求轨迹方程时,特别要注意其取值范围.
以抛物线y=x2的弦AB为直径的圆经过原点O,过点O作OM⊥AB,M为垂足,求点M的轨迹方程.
活动三 直线与圆锥曲线的有关问题
例3 设直线l过双曲线x2-=1的一个焦点,且交双曲线于A,B两点,O为坐标原点,若·=0,求AB的值.
对于直线与圆锥曲线的位置关系,通常采用代数的方法(建立方程组)去研究.
(2024山西芮城中学期末)已知椭圆C:+=1(a>b>0)的两个焦点为F1(-2,0),F2(2,0),点M(2,)在椭圆C上.
(1) 求椭圆C的标准方程;
(2) 若过点P(-8,0)的直线与椭圆C交于A,B两点,求证:△ABF1的内心在一条定直线上.
活动四 求取值范围或最值
例4 动点P到定点F(0,1)的距离比它到直线y=-2的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A,B两个不同的点,过点A,B分别作曲线C的切线,且二者相交于点M.
(1) 求曲线C的方程;
(2) 求证:·=0;
(3) 求△ABM的面积的最小值.
圆锥曲线中的最值问题一般采用代数的方法,即列出求解的表达式,再根据变量的取值范围解决这个式子的最值问题.有时也根据题中的图形特征,用几何的方法解决其最值问题.
已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1).若右焦点到直线x-y+2=0 的距离为3.
(1) 求椭圆的标准方程;
(2) 设椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N.当AM=AN时,求实数m的取值范围.
1. (2025江西师大附中期末)已知斜率为的直线过抛物线C:y2=4x的焦点,且与抛物线C交于A,B两点,则AB的长为( )
A. 2 B. C. 1 D.
2. (2024海门期末)下列直线被椭圆C:+y2=1截得的弦长大于l:y=x+1被椭圆C截得的弦长的是( )
A. y=-x B. y=-x-1 C. y=x-1 D. y=x+
3. (多选)(2025开封期末)已知平面内与两定点A1(-a,0),A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1,A2两点所形成的曲线C可以是( )
A. 若m=-1,曲线C是圆心在原点的圆
B. 若m<-1,曲线C是焦点在x轴上的椭圆
C. 若-1D. 若m>0,曲线C是焦点在x轴上的双曲线
4. 已知抛物线C:x2=4y的焦点为F,点A(3,4),P为抛物线C上一点,则PA+PF的最小值为________.
5. 设双曲线-=1(a>0)的两个焦点分别为F1,F2,离心率为2.
(1) 求此双曲线的渐近线方程;
(2) 若点A,B在不同的渐近线上,且2AB=5F1F2,求线段AB的中点M的轨迹方程.
第3章 圆锥曲线与方程
本 章 复 习
【活动方案】
2. 略
例1 (1) 根据题意可得=,化简,得x2+=1,
所以曲线E的方程为x2+=1.
(2) 由题意可知PQ=
=
=(-1≤x≤1),
当-<-1,即 m>2 时,由PQmax=|m+1|=,解得m=-1(舍去);
当-1≤-<-,即 1<m≤2 时,由PQmax==,解得m=.
综上所述,实数m的值为.
跟踪训练 (1) 由题意可知F1F1=2,且MF1+MF2+F1F2=×12=6,
所以MF1+MF2=4>F1F2=2,
所以点M的轨迹是以F1(-1,0)和F2(1,0)为焦点,长轴长为4的椭圆.
因为三个中点不能共线,
所以点M不落在x轴上.
综上,所求轨迹方程为+=1(y≠0).
(2) 设点M(x1,y1),N(x2,y2),显然直线MF1不与x轴重合,不妨设直线MF1的方程为x=ty-1,
与椭圆方程+=1(y≠0)联立,消去x并整理,得(3t2+4)y2-6ty-9=0,Δ=36t2+36(3t2+4)=144(t2+1)>0,
则y1+y2=,y1y2=-<0.
因为S△NF1O=F1O·|y2|=|y2|,
S△MF1E=S△MF1F2=×F1F2·|y1|=|y1|,
所以S=S△NF1O+S△MF1E=(|y1|+|y2|)
=|y1-y2|=·=.
令u=3t2+4(u≥4),
则S=φ(u)==6
=6.
因为u≥4,所以0<≤,
所以当=,即t=0时,Smax=.
故当直线MN⊥x轴时,S的最大值为.
例2 D 设P(m,n)(0≤m≤2,-1≤n≤0).因为直线OB的方程为y=-x,且点M在直线OB上,所以点M.因为直线OP的方程为y=x,且点E在直线OP上,所以点E.因为ME∥x轴,所以-=,则m2=-4n(0≤m≤2),故D正确.
跟踪训练 设直线OA的方程为y=kx,代入y=x2,得点A(4k,4k2).
因为OA⊥OB,所以kOB=-,
同理可得点B(-,),
所以直线AB的方程为y-4k2=(x-4k),
即y-4=x,①
直线OM的方程为y=-x,②
①×②,得y2-4y=-x2,
故点M的轨迹方程为x2+y2-4y=0(y≠0).
例3 不妨设直线l过右焦点(2,0),当AB⊥x轴时,易得点A(2,3),B(2,-3),不满足条件,则直线AB的斜率存在,设为k,故直线AB的方程为 y=k(x-2),
代入双曲线方程,消去y并整理,得
(3-k2)x2+4k2x-4k2-3=0,
则Δ=16k4+4(3-k2)(4k2+3)>0.
设点A(x1,y1),B(x2,y2),
则x1+x2=,x1x2=,
所以y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]=-.
因为·=0,所以x1x2+y1y2=0,
所以-=0,解得k2=,
满足Δ>0,
所以x1+x2==-1,x1x2==-,
故AB=|x1-x2|=4.
跟踪训练 (1) 因为椭圆两个焦点为F1(-2,0),F2(2,0),
所以c=2,则a2=b2+4.
又点M(2,)在椭圆C上,
所以+=1,即+=1,
两式联立,解得a2=16,b2=12,
所以椭圆C的标准方程为+=1.
(2) 由题意,得直线AB的斜率存在,且不为0,设直线AB的方程为x=my-8,
联立消去x并整理,得(3m2+4)y2-48my+144=0,
则Δ=(-48m)2-4(3m2+4)×144=576m2-2 304>0,得m2>4.
设点A(x1,y1),B(x2,y2),
则y1+y2=,y1y2=.
设直线AF1,BF1的斜率分别为k1,k2,
所以k1+k2=+=+=,
因为y1(my2-6)+y2(my1-6)=2my1y2-6(y1+y2)=2m×-6×=0,
所以k1+k2=0恒成立,则直线AF1,BF1的倾斜角互补,
即∠AF1B的平分线总垂直于x轴,
所以△ABF1的内心在定直线x=-2上.
例4 (1) 由题意可知动点P到定点F(0,1)的距离等于它到直线y=-1的距离,
所以动点P的轨迹是以F(0,1)为焦点,直线y=-1为准线的抛物线,
所以曲线C的方程为x2=4y.
(2) 设直线AB的方程为y=kx+1,
由得x2-4kx-4=0.
设点A(xA,yA),B(xB,yB),
则xA+xB=4k,xA·xB=-4.
设过点A的切线方程为y=kA(x-xA)+yA,
与x2=4y联立,得x2-4kAx+4kAxA-x=0,
由Δ=0,可得kA=xA,
同理,过点B的切线斜率kB=xB,
所以直线AM的方程为xAx=2(y+yA),①
直线BM的方程为xBx=2(y+yB),②
①-②,得x(xA-xB)=2(yA-yB)=(x-x),即x==2k,
将x=代入①,得y=-1,
故M(2k,-1),
所以=(-2k,2),=(xB-xA,k(xB-xA)),
所以·=-2k(xB-xA)+2k(xB-xA)=0.
(3) 由(2)知,点M到AB的距离d=MF=2.
因为AB=AF+BF=yA+yB+2=k(xA+xB)+4=4k2+k,
所以S=AB·d=×4(k2+1)×2=4≥4,
所以当k=0时,△ABM的面积有最小值4.
跟踪训练 (1) 由题意,可设椭圆方程为 +y2=1(a>0),则右焦点F(,0).
又因为右焦点到直线x-y+2=0的距离为3,
所以=3,解得a2=3.
故所求椭圆的标准方程为+y2=1.
(2) 设P为MN的中点,由
得 (3k2+1)x2+6mkx+3(m2-1)=0.
因为直线与椭圆有两个交点,所以Δ>0,
即 m2<3k2+1,①
所以xP==-,
所以yP=kxP+m=,
所以kAP==-.
又AM=AN,
所以AP⊥MN,则-=-,
即 2m=3k2+1.②
将②代入①,得 2m>m2,解得0又由②,得 k2=>0,解得m>,
故实数m的取值范围是(,2).
【检测反馈】
1. B 由题意,得抛物线C:y2=4x的焦点为(1,0),p=2,故斜率为且过点(1,0)的直线方程为y=(x-1).设点A(x1,y1),B(x2,y2),联立消去y并整理,得3x2-10x+3=0,可得x1+x2=,所以AB=x1+x2+p=+2=.
2. A 易知椭圆C:+y2=1关于x轴,y轴,原点对称,直线y=x+1与直线y=-x-1关于x轴对称,直线y=x+1与直线y=x-1关于原点对称,所以直线y=x+1,y=-x-1,y=x-1被椭圆所截得的弦长相等,故B,C错误;根据椭圆的对称性可知原点到直线的距离越大,直线被椭圆截得的弦长越小,y=-x过原点,y=x+比y=x+1到原点的距离远,故y=x+截椭圆所得的弦长比y=x+1截椭圆的弦长要短,故A正确,D错误.
3. ACD 设点M(x,y),当x≠±a时,由kMA1·kMA2=·=m,即y2=m(x2-a2)(x≠±a).又点A1(-a,0),A2(a,0)的坐标满足y2=m(x2-a2).对于A,当m=-1时,曲线C的方程为x2+y2=a2,曲线C是圆心在原点的圆,故A正确;对于B,当m=-2时,曲线C的方程为+=1,曲线C为焦点在y轴上的椭圆,故B错误;对于C,当-10时,+=1,曲线C是焦点在x轴上的双曲线,故D正确.故选ACD.
4. 5 如图,过点P作准线的垂线,垂足为B,则PA+PF=PA+PB.显然点A在抛物线内,则当P,A,B三点共线时,PA+PB最小,其最小值为 4+1=5.
5. (1) 因为e=2,所以c2=4a2.
因为c2=a2+3,所以a=1,c=2,
所以双曲线方程为y2-=1,渐近线方程为y=±x.
(2) 不妨设点A在直线y=x上,点B在直线 y=-x上,点A(x1,y1),B(x2,y2),AB的中点为M(x,y).
因为2AB=5F1F2=5×2c=20,
所以AB=10,
所以=10,
即(x1-x2)2+(y1-y2)2=100.
因为y1=x1,y2=-x2,x1+x2=2x,y1+y2=2y,
所以y1+y2=(x1-x2),y1-y2=(x1+x2),
所以y=(x1-x2),y1-y2=x,
代入(x1-x2)2+(y1-y2)2=100,
得3×(2y)2+(2x)2=100,
整理,得+=1,
即线段AB的中点M的轨迹方程为+=1.
本 章 复 习
1. 梳理本章知识,构建知识网络.
2. 巩固椭圆、双曲线、抛物线的概念及其几何性质.
3. 掌握直线与圆锥曲线的位置关系的综合应用及圆锥曲线性质的应用.
活动一 理解与圆锥曲线相关的基本知识
1. 知识结构框图
2. 知识能力整合
三种圆锥曲线的定义、标准方程及几何性质:
椭圆 双曲线 抛物线
统一定义
各自定义
标准方程 +=1(a>b>0) -=1(a>0,b>0) y2=2px(p>0)
图 形
焦点坐标
对称性
顶点坐标
离心率
准线方程
渐近线方程 —— ——
活动二 圆锥曲线的方程与性质
例1 已知点P(x,y)到定点F(0,)的距离与它到定直线l:y=的距离的比是常数,点P 的轨迹为曲线E.
(1) 求曲线E的方程;
(2) 设点Q(m,0)(m>1),若PQ的最大值为,求实数m的值.
根据条件先判断动点的轨迹,再求其轨迹方程.
在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(-1,0)和F2(1,0),M为BC边的中点.
(1) 求点M的轨迹方程;
(2) 设点M的轨迹为曲线Γ,直线MF1与曲线Γ的另一个交点为N,线段MF2的中点为E,记 S=S△NF1O+S△MF1E,求S的最大值.
例2 (2024苏州调研)如图,已知点B(2,-1),BC⊥x轴于点C,M是线段OB上任意一点,MD⊥x轴于点D,ME⊥BC于点E,OE与MD相交于点P,则点P的轨迹方程为( )
A. y2=x(0≤x≤2)
B. y2=x(0≤x≤2)
C. x2=-y(0≤x≤2)
D. x2=-4y(0≤x≤2)
消参求轨迹方程时,特别要注意其取值范围.
以抛物线y=x2的弦AB为直径的圆经过原点O,过点O作OM⊥AB,M为垂足,求点M的轨迹方程.
活动三 直线与圆锥曲线的有关问题
例3 设直线l过双曲线x2-=1的一个焦点,且交双曲线于A,B两点,O为坐标原点,若·=0,求AB的值.
对于直线与圆锥曲线的位置关系,通常采用代数的方法(建立方程组)去研究.
(2024山西芮城中学期末)已知椭圆C:+=1(a>b>0)的两个焦点为F1(-2,0),F2(2,0),点M(2,)在椭圆C上.
(1) 求椭圆C的标准方程;
(2) 若过点P(-8,0)的直线与椭圆C交于A,B两点,求证:△ABF1的内心在一条定直线上.
活动四 求取值范围或最值
例4 动点P到定点F(0,1)的距离比它到直线y=-2的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A,B两个不同的点,过点A,B分别作曲线C的切线,且二者相交于点M.
(1) 求曲线C的方程;
(2) 求证:·=0;
(3) 求△ABM的面积的最小值.
圆锥曲线中的最值问题一般采用代数的方法,即列出求解的表达式,再根据变量的取值范围解决这个式子的最值问题.有时也根据题中的图形特征,用几何的方法解决其最值问题.
已知椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1).若右焦点到直线x-y+2=0 的距离为3.
(1) 求椭圆的标准方程;
(2) 设椭圆与直线y=kx+m(k≠0)相交于不同的两点M,N.当AM=AN时,求实数m的取值范围.
1. (2025江西师大附中期末)已知斜率为的直线过抛物线C:y2=4x的焦点,且与抛物线C交于A,B两点,则AB的长为( )
A. 2 B. C. 1 D.
2. (2024海门期末)下列直线被椭圆C:+y2=1截得的弦长大于l:y=x+1被椭圆C截得的弦长的是( )
A. y=-x B. y=-x-1 C. y=x-1 D. y=x+
3. (多选)(2025开封期末)已知平面内与两定点A1(-a,0),A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1,A2两点所形成的曲线C可以是( )
A. 若m=-1,曲线C是圆心在原点的圆
B. 若m<-1,曲线C是焦点在x轴上的椭圆
C. 若-1
4. 已知抛物线C:x2=4y的焦点为F,点A(3,4),P为抛物线C上一点,则PA+PF的最小值为________.
5. 设双曲线-=1(a>0)的两个焦点分别为F1,F2,离心率为2.
(1) 求此双曲线的渐近线方程;
(2) 若点A,B在不同的渐近线上,且2AB=5F1F2,求线段AB的中点M的轨迹方程.
第3章 圆锥曲线与方程
本 章 复 习
【活动方案】
2. 略
例1 (1) 根据题意可得=,化简,得x2+=1,
所以曲线E的方程为x2+=1.
(2) 由题意可知PQ=
=
=(-1≤x≤1),
当-<-1,即 m>2 时,由PQmax=|m+1|=,解得m=-1(舍去);
当-1≤-<-,即 1<m≤2 时,由PQmax==,解得m=.
综上所述,实数m的值为.
跟踪训练 (1) 由题意可知F1F1=2,且MF1+MF2+F1F2=×12=6,
所以MF1+MF2=4>F1F2=2,
所以点M的轨迹是以F1(-1,0)和F2(1,0)为焦点,长轴长为4的椭圆.
因为三个中点不能共线,
所以点M不落在x轴上.
综上,所求轨迹方程为+=1(y≠0).
(2) 设点M(x1,y1),N(x2,y2),显然直线MF1不与x轴重合,不妨设直线MF1的方程为x=ty-1,
与椭圆方程+=1(y≠0)联立,消去x并整理,得(3t2+4)y2-6ty-9=0,Δ=36t2+36(3t2+4)=144(t2+1)>0,
则y1+y2=,y1y2=-<0.
因为S△NF1O=F1O·|y2|=|y2|,
S△MF1E=S△MF1F2=×F1F2·|y1|=|y1|,
所以S=S△NF1O+S△MF1E=(|y1|+|y2|)
=|y1-y2|=·=.
令u=3t2+4(u≥4),
则S=φ(u)==6
=6.
因为u≥4,所以0<≤,
所以当=,即t=0时,Smax=.
故当直线MN⊥x轴时,S的最大值为.
例2 D 设P(m,n)(0≤m≤2,-1≤n≤0).因为直线OB的方程为y=-x,且点M在直线OB上,所以点M.因为直线OP的方程为y=x,且点E在直线OP上,所以点E.因为ME∥x轴,所以-=,则m2=-4n(0≤m≤2),故D正确.
跟踪训练 设直线OA的方程为y=kx,代入y=x2,得点A(4k,4k2).
因为OA⊥OB,所以kOB=-,
同理可得点B(-,),
所以直线AB的方程为y-4k2=(x-4k),
即y-4=x,①
直线OM的方程为y=-x,②
①×②,得y2-4y=-x2,
故点M的轨迹方程为x2+y2-4y=0(y≠0).
例3 不妨设直线l过右焦点(2,0),当AB⊥x轴时,易得点A(2,3),B(2,-3),不满足条件,则直线AB的斜率存在,设为k,故直线AB的方程为 y=k(x-2),
代入双曲线方程,消去y并整理,得
(3-k2)x2+4k2x-4k2-3=0,
则Δ=16k4+4(3-k2)(4k2+3)>0.
设点A(x1,y1),B(x2,y2),
则x1+x2=,x1x2=,
所以y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]=-.
因为·=0,所以x1x2+y1y2=0,
所以-=0,解得k2=,
满足Δ>0,
所以x1+x2==-1,x1x2==-,
故AB=|x1-x2|=4.
跟踪训练 (1) 因为椭圆两个焦点为F1(-2,0),F2(2,0),
所以c=2,则a2=b2+4.
又点M(2,)在椭圆C上,
所以+=1,即+=1,
两式联立,解得a2=16,b2=12,
所以椭圆C的标准方程为+=1.
(2) 由题意,得直线AB的斜率存在,且不为0,设直线AB的方程为x=my-8,
联立消去x并整理,得(3m2+4)y2-48my+144=0,
则Δ=(-48m)2-4(3m2+4)×144=576m2-2 304>0,得m2>4.
设点A(x1,y1),B(x2,y2),
则y1+y2=,y1y2=.
设直线AF1,BF1的斜率分别为k1,k2,
所以k1+k2=+=+=,
因为y1(my2-6)+y2(my1-6)=2my1y2-6(y1+y2)=2m×-6×=0,
所以k1+k2=0恒成立,则直线AF1,BF1的倾斜角互补,
即∠AF1B的平分线总垂直于x轴,
所以△ABF1的内心在定直线x=-2上.
例4 (1) 由题意可知动点P到定点F(0,1)的距离等于它到直线y=-1的距离,
所以动点P的轨迹是以F(0,1)为焦点,直线y=-1为准线的抛物线,
所以曲线C的方程为x2=4y.
(2) 设直线AB的方程为y=kx+1,
由得x2-4kx-4=0.
设点A(xA,yA),B(xB,yB),
则xA+xB=4k,xA·xB=-4.
设过点A的切线方程为y=kA(x-xA)+yA,
与x2=4y联立,得x2-4kAx+4kAxA-x=0,
由Δ=0,可得kA=xA,
同理,过点B的切线斜率kB=xB,
所以直线AM的方程为xAx=2(y+yA),①
直线BM的方程为xBx=2(y+yB),②
①-②,得x(xA-xB)=2(yA-yB)=(x-x),即x==2k,
将x=代入①,得y=-1,
故M(2k,-1),
所以=(-2k,2),=(xB-xA,k(xB-xA)),
所以·=-2k(xB-xA)+2k(xB-xA)=0.
(3) 由(2)知,点M到AB的距离d=MF=2.
因为AB=AF+BF=yA+yB+2=k(xA+xB)+4=4k2+k,
所以S=AB·d=×4(k2+1)×2=4≥4,
所以当k=0时,△ABM的面积有最小值4.
跟踪训练 (1) 由题意,可设椭圆方程为 +y2=1(a>0),则右焦点F(,0).
又因为右焦点到直线x-y+2=0的距离为3,
所以=3,解得a2=3.
故所求椭圆的标准方程为+y2=1.
(2) 设P为MN的中点,由
得 (3k2+1)x2+6mkx+3(m2-1)=0.
因为直线与椭圆有两个交点,所以Δ>0,
即 m2<3k2+1,①
所以xP==-,
所以yP=kxP+m=,
所以kAP==-.
又AM=AN,
所以AP⊥MN,则-=-,
即 2m=3k2+1.②
将②代入①,得 2m>m2,解得0
故实数m的取值范围是(,2).
【检测反馈】
1. B 由题意,得抛物线C:y2=4x的焦点为(1,0),p=2,故斜率为且过点(1,0)的直线方程为y=(x-1).设点A(x1,y1),B(x2,y2),联立消去y并整理,得3x2-10x+3=0,可得x1+x2=,所以AB=x1+x2+p=+2=.
2. A 易知椭圆C:+y2=1关于x轴,y轴,原点对称,直线y=x+1与直线y=-x-1关于x轴对称,直线y=x+1与直线y=x-1关于原点对称,所以直线y=x+1,y=-x-1,y=x-1被椭圆所截得的弦长相等,故B,C错误;根据椭圆的对称性可知原点到直线的距离越大,直线被椭圆截得的弦长越小,y=-x过原点,y=x+比y=x+1到原点的距离远,故y=x+截椭圆所得的弦长比y=x+1截椭圆的弦长要短,故A正确,D错误.
3. ACD 设点M(x,y),当x≠±a时,由kMA1·kMA2=·=m,即y2=m(x2-a2)(x≠±a).又点A1(-a,0),A2(a,0)的坐标满足y2=m(x2-a2).对于A,当m=-1时,曲线C的方程为x2+y2=a2,曲线C是圆心在原点的圆,故A正确;对于B,当m=-2时,曲线C的方程为+=1,曲线C为焦点在y轴上的椭圆,故B错误;对于C,当-1
4. 5 如图,过点P作准线的垂线,垂足为B,则PA+PF=PA+PB.显然点A在抛物线内,则当P,A,B三点共线时,PA+PB最小,其最小值为 4+1=5.
5. (1) 因为e=2,所以c2=4a2.
因为c2=a2+3,所以a=1,c=2,
所以双曲线方程为y2-=1,渐近线方程为y=±x.
(2) 不妨设点A在直线y=x上,点B在直线 y=-x上,点A(x1,y1),B(x2,y2),AB的中点为M(x,y).
因为2AB=5F1F2=5×2c=20,
所以AB=10,
所以=10,
即(x1-x2)2+(y1-y2)2=100.
因为y1=x1,y2=-x2,x1+x2=2x,y1+y2=2y,
所以y1+y2=(x1-x2),y1-y2=(x1+x2),
所以y=(x1-x2),y1-y2=x,
代入(x1-x2)2+(y1-y2)2=100,
得3×(2y)2+(2x)2=100,
整理,得+=1,
即线段AB的中点M的轨迹方程为+=1.
