华师大版数学七年级上册4.2.2由视图到立体图形
文档属性
| 名称 | 华师大版数学七年级上册4.2.2由视图到立体图形 |
|
|
| 格式 | doc | ||
| 文件大小 | 257.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-17 11:53:45 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学七年级上册4.2.2由视图到立体图形同步练习
一、选择题
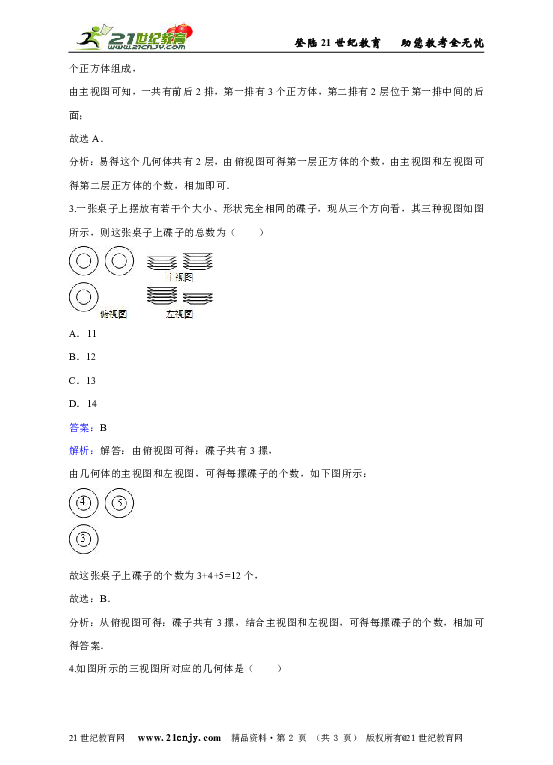
1.一个几何体的三视图如图所示,则这个几何体是( )
A.圆柱
B.圆锥
C.长方体
D.正方体
答案:A
解析:解答:由主视图和左视图为长方形可得此几何体为柱体,由俯视图为圆可得此几何体为圆柱.
故选A.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
2.如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
A.
B.
C.
D.
答案:A
解析:解答:由俯视图易得最底层有4个正方体,第二层有1个正方体,那么共有4+1=5个正方体组成,
由主视图可知,一共有前后2排,第一排有3个正方体,第二排有2层位于第一排中间的后面;
故选A.
分析:易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.
3.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
答案:B
解析:解答:由俯视图可得:碟子共有3摞,
由几何体的主视图和左视图,可得每摞碟子的个数,如下图所示:
故这张桌子上碟子的个数为3+4+5=12个,
故选:B.
分析:从俯视图可得:碟子共有3摞,结合主视图和左视图,可得每摞碟子的个数,相加可得答案.
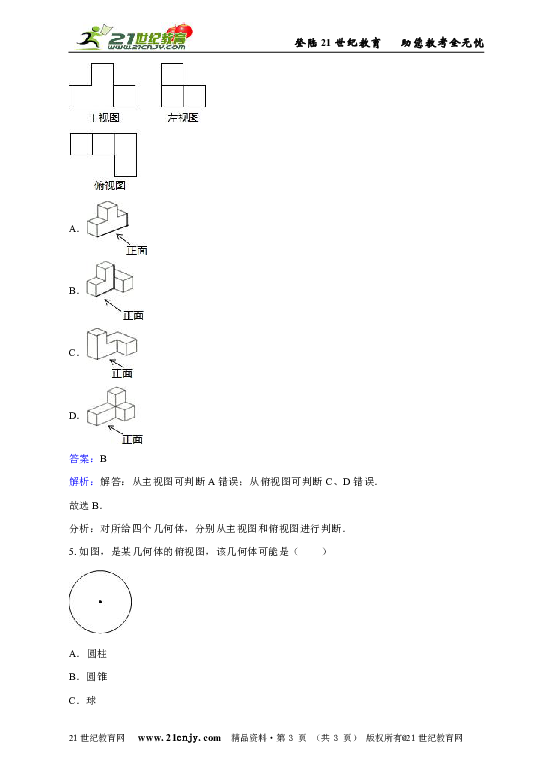
4.如图所示的三视图所对应的几何体是( )
A.
B.
C.
D.
答案:B
解析:解答:从主视图可判断A错误;从俯视图可判断C、D错误.
故选B.
分析:对所给四个几何体,分别从主视图和俯视图进行判断.
5.如图,是某几何体的俯视图,该几何体可能是( )
A.圆柱
B.圆锥
C.球
D.正方体
答案:B
解析:解答:圆柱的俯视图是圆,A错误;
圆锥的俯视图是圆,且中心由一个实点,B正确;
球的俯视图是圆,C错误;
正方体的俯视图是正方形,D错误.
故选:B.
分析:根据几何体的俯视图是从上面看,所得到的图形分别写出各个几何体的俯视图判断即可.
6.一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
答案:B
解析:解答:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选:B.
分析:根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱.
7.下列四个物体的俯视图与右边给出视图一致的是( )
A.
B.
C.
D.
答案:C
解析:解答:几何体的俯视图为,
故选C.
分析:从上面看几何体,得到俯视图,即可做出判断.
8.如图是某几何体的三视图,该几何体是( )
A.圆柱
B.圆锥
C.正三棱柱
D.正三棱锥
答案:B
解析:解答:根据几何体的三视图即可知道几何体是圆锥.
故选B.
分析:根据三视图易得此几何体为圆锥.
9.若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是( )
A.正方体
B.圆锥
C.圆柱
D.球
答案:A
解析:解答:∵主视图和左视图都是正方形,
∴此几何体为柱体,
∵俯视图是一个正方形,
∴此几何体为正方体.
故选A.
分析:找到从正面、左面和上面看得到的图形是正方形的几何体即可.
10.如图,是由若干个相同的小立方体搭成的几何体生物俯视图和左视图.则小立方体的个数可能是( )
A.5或6
B.5或7
C.4或5或6
D.5或6或7
答案:D
解析:解答:由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3个小立方体和最少有1个小立方体,
那么小立方体的个数可能是5个或6个或7个.
故选D.
分析:易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层最多和最少小立方体的个数,相加即可.
11.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4
B.5
C.6
D.9
答案:A
解析:解答:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故选A.
分析:根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两层3列,故可得出该几何体的小正方体的个数.
12.如图,甲、乙、丙图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同
B.仅有甲和丙相同
C.仅有乙和丙相同
D.甲、乙、丙都相同
答案:B
解析:解答:根据分析可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2;
则主视图相同的是甲和丙.
故选:B.
分析:由已知条件可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2.据此可即可求解.
13.如图是一个几何体的三视图,则这个几何体是( )
A.正方体
B.长方体
C.三棱柱
D.三棱锥
答案:B
解析:解答:根据主视图和左视图为矩形是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体.
故选:B.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
14.一个几何体的三视图如图所示,则该几何体的形状可能是( )
A.
B.
C.
D.
答案:D
解析:解答:由主视图和左视图可得此几何体上面为台,下面为柱体,
由俯视图为圆环可得几何体为.
故选D.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
15.一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图与俯视图如图所示,根据小明画的视图,请你猜礼物是( )
A.钢笔
B.生日蛋糕
C.光盘
D.一套衣服
答案:B
解析:解答:根据主视图为矩形判断出两个几何体是柱体,根据俯视图是圆可判断出这2个几何体应该都是圆柱,故选B.
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
二、填空题
16.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是______个.
答案:7
解析:解答:根据题意得:
,
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为:7.
分析:根据几何体主视图,在俯视图上表上数字,即可得出搭成该几何体的小正方体最多的个数.
17.一个几何体的三视图如图所示,那么这个几何体的侧面积是______(结果保留π)
答案:6π
解析:解答:∵圆柱的直径为2,高为3,
∴侧面积为.
故答案为:6π.
分析:根据三视图正视图以及左视图都为矩形,底面是圆形,则可想象出这是一个圆柱体.侧面积=底面周长×高.
18.长方体的主视图、俯视图如图,则其左视图面积为______.
答案:3
解析:解答:由主视图可得长方体的高为1,长为4,
由俯视图可得宽为3,
则左视图的面积为3×1=3;
故答案为:3.
分析:根据主视图可得到长方体的长和高,俯视图可得到长方体的宽,左视图表现长方体的宽和高,让宽×高即为左视图的面积.
19.下列是由几块小立方块搭成的几何体的主视图与左视图,这个几何体最多可能有______个小立方块.
答案:9
解析:解答:∵由主视图可得组合几何体的底层有3列,由左视图可得该几何体有2行,
∴最底层最多有3×2=6个正方体,主视图和左视图可得第2层最多有1+1=2个正方体,最上一层最多有1个正方体,
∴组成该几何体的正方体最多有6+2+1=9个,.
故答案为:9.
分析:由主视图可得组合几何体的底层有3列,由左视图可得该几何体有2行,所以最底层最多有3×2=6个正方体,由主视图和左视图可得第2层最多有1+1=3个正方体,最上一层最多有1个正方体,相加可得组成组合几何体的正方体的个数.
20.如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是______.
答案:4
解析:解答:因为第一列小立方体的个数最少为1+1,第二列的个数最少是1+1,
所以这个几何体最少由1+1+1+1=4个小立方块搭成;
故答案为:4.
分析:第一列小立方体的个数最少为1+1,第二列的个数最少是1+1,两列小立方体的个数相加即可.
三、解答题
21.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
答案:
解答:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,
高H为150毫米,
∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴.
答:制作每个密封罐所需钢板的面积为.
解析:分析:首先利用几何体的三视图确定该几何体的形状,然后计算其表面积.
22.某一空间图形的三视图如图,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的圆以及高为1的矩形;俯视图:半径为1的圆.求此图形的体积.
答案:
解答:根据题意,该图形为圆柱和一个的球的组合体,
球体积应为,
圆柱体积,
则图形的体积是:.
解析:分析:由已知中的三视图,可以判断出该几何体的形状为:下部是底面半径为1,高为1的圆柱,上部为半径为1的球,组成的组合体,代入圆柱体积公式和球的体积公式,即可得到答案.
23.下面的图形是一个物体的三视图,请画出这个物体的形状.
答案:解答:如图:
解析:分析:由立体图形的三视图可得立体图形有3列,且第一列是前后两个立方体,且后面一个上面有一个立方体,第二、三列是一个立方体,进而画出图形.
24.如图是由几个小正方体所搭成的几何体上面看到的图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出从正面、左面可以看到的图形.
答案:解答:作图如下:
解析:分析:由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,4;左视图有2列,每列小正方形数目分别为4,2.据此可画出图形.
25.如图是由几个小正方体所搭成的几何体上面看到的图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出从正面、左面可以看到的图形.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
答案:最多需要17个小正方体,最少需要11个小正方体.
解答:搭这样的几何体最少需要8+2+1=11个小正方体,
最多需要8+6+3=17个小正方体;
故最多需要17个小正方体,最少需要11个小正方体.
解析:分析:易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 14 页) 版权所有@21世纪教育网
华师大版数学七年级上册4.2.2由视图到立体图形同步练习
一、选择题
1.一个几何体的三视图如图所示,则这个几何体是( )
A.圆柱
B.圆锥
C.长方体
D.正方体
答案:A
解析:解答:由主视图和左视图为长方形可得此几何体为柱体,由俯视图为圆可得此几何体为圆柱.
故选A.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
2.如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
A.
B.
C.
D.
答案:A
解析:解答:由俯视图易得最底层有4个正方体,第二层有1个正方体,那么共有4+1=5个正方体组成,
由主视图可知,一共有前后2排,第一排有3个正方体,第二排有2层位于第一排中间的后面;
故选A.
分析:易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.
3.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11
B.12
C.13
D.14
答案:B
解析:解答:由俯视图可得:碟子共有3摞,
由几何体的主视图和左视图,可得每摞碟子的个数,如下图所示:
故这张桌子上碟子的个数为3+4+5=12个,
故选:B.
分析:从俯视图可得:碟子共有3摞,结合主视图和左视图,可得每摞碟子的个数,相加可得答案.
4.如图所示的三视图所对应的几何体是( )
A.
B.
C.
D.
答案:B
解析:解答:从主视图可判断A错误;从俯视图可判断C、D错误.
故选B.
分析:对所给四个几何体,分别从主视图和俯视图进行判断.
5.如图,是某几何体的俯视图,该几何体可能是( )
A.圆柱
B.圆锥
C.球
D.正方体
答案:B
解析:解答:圆柱的俯视图是圆,A错误;
圆锥的俯视图是圆,且中心由一个实点,B正确;
球的俯视图是圆,C错误;
正方体的俯视图是正方形,D错误.
故选:B.
分析:根据几何体的俯视图是从上面看,所得到的图形分别写出各个几何体的俯视图判断即可.
6.一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥
B.三棱柱
C.圆柱
D.长方体
答案:B
解析:解答:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选:B.
分析:根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱.
7.下列四个物体的俯视图与右边给出视图一致的是( )
A.
B.
C.
D.
答案:C
解析:解答:几何体的俯视图为,
故选C.
分析:从上面看几何体,得到俯视图,即可做出判断.
8.如图是某几何体的三视图,该几何体是( )
A.圆柱
B.圆锥
C.正三棱柱
D.正三棱锥
答案:B
解析:解答:根据几何体的三视图即可知道几何体是圆锥.
故选B.
分析:根据三视图易得此几何体为圆锥.
9.若一个几何体的主视图、左视图、俯视图都是正方形,则这个几何体是( )
A.正方体
B.圆锥
C.圆柱
D.球
答案:A
解析:解答:∵主视图和左视图都是正方形,
∴此几何体为柱体,
∵俯视图是一个正方形,
∴此几何体为正方体.
故选A.
分析:找到从正面、左面和上面看得到的图形是正方形的几何体即可.
10.如图,是由若干个相同的小立方体搭成的几何体生物俯视图和左视图.则小立方体的个数可能是( )
A.5或6
B.5或7
C.4或5或6
D.5或6或7
答案:D
解析:解答:由俯视图易得最底层有4个小立方体,由左视图易得第二层最多有3个小立方体和最少有1个小立方体,
那么小立方体的个数可能是5个或6个或7个.
故选D.
分析:易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层最多和最少小立方体的个数,相加即可.
11.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4
B.5
C.6
D.9
答案:A
解析:解答:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故选A.
分析:根据三视图,该几何体的主视图以及俯视图可确定该几何体共有两层3列,故可得出该几何体的小正方体的个数.
12.如图,甲、乙、丙图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同
B.仅有甲和丙相同
C.仅有乙和丙相同
D.甲、乙、丙都相同
答案:B
解析:解答:根据分析可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2;
则主视图相同的是甲和丙.
故选:B.
分析:由已知条件可知,甲的主视图有2列,每列小正方数形数目分别为2,2;乙的主视图有2列,每列小正方数形数目分别为2,1;丙的主视图有2列,每列小正方数形数目分别为2,2.据此可即可求解.
13.如图是一个几何体的三视图,则这个几何体是( )
A.正方体
B.长方体
C.三棱柱
D.三棱锥
答案:B
解析:解答:根据主视图和左视图为矩形是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体.
故选:B.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
14.一个几何体的三视图如图所示,则该几何体的形状可能是( )
A.
B.
C.
D.
答案:D
解析:解答:由主视图和左视图可得此几何体上面为台,下面为柱体,
由俯视图为圆环可得几何体为.
故选D.
分析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
15.一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图与俯视图如图所示,根据小明画的视图,请你猜礼物是( )
A.钢笔
B.生日蛋糕
C.光盘
D.一套衣服
答案:B
解析:解答:根据主视图为矩形判断出两个几何体是柱体,根据俯视图是圆可判断出这2个几何体应该都是圆柱,故选B.
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
二、填空题
16.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是______个.
答案:7
解析:解答:根据题意得:
,
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为:7.
分析:根据几何体主视图,在俯视图上表上数字,即可得出搭成该几何体的小正方体最多的个数.
17.一个几何体的三视图如图所示,那么这个几何体的侧面积是______(结果保留π)
答案:6π
解析:解答:∵圆柱的直径为2,高为3,
∴侧面积为.
故答案为:6π.
分析:根据三视图正视图以及左视图都为矩形,底面是圆形,则可想象出这是一个圆柱体.侧面积=底面周长×高.
18.长方体的主视图、俯视图如图,则其左视图面积为______.
答案:3
解析:解答:由主视图可得长方体的高为1,长为4,
由俯视图可得宽为3,
则左视图的面积为3×1=3;
故答案为:3.
分析:根据主视图可得到长方体的长和高,俯视图可得到长方体的宽,左视图表现长方体的宽和高,让宽×高即为左视图的面积.
19.下列是由几块小立方块搭成的几何体的主视图与左视图,这个几何体最多可能有______个小立方块.
答案:9
解析:解答:∵由主视图可得组合几何体的底层有3列,由左视图可得该几何体有2行,
∴最底层最多有3×2=6个正方体,主视图和左视图可得第2层最多有1+1=2个正方体,最上一层最多有1个正方体,
∴组成该几何体的正方体最多有6+2+1=9个,.
故答案为:9.
分析:由主视图可得组合几何体的底层有3列,由左视图可得该几何体有2行,所以最底层最多有3×2=6个正方体,由主视图和左视图可得第2层最多有1+1=3个正方体,最上一层最多有1个正方体,相加可得组成组合几何体的正方体的个数.
20.如图是由几个相同的小立方体组成的左视图和俯视图,小立方块的个数最少是______.
答案:4
解析:解答:因为第一列小立方体的个数最少为1+1,第二列的个数最少是1+1,
所以这个几何体最少由1+1+1+1=4个小立方块搭成;
故答案为:4.
分析:第一列小立方体的个数最少为1+1,第二列的个数最少是1+1,两列小立方体的个数相加即可.
三、解答题
21.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
答案:
解答:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,
高H为150毫米,
∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴.
答:制作每个密封罐所需钢板的面积为.
解析:分析:首先利用几何体的三视图确定该几何体的形状,然后计算其表面积.
22.某一空间图形的三视图如图,其中主视图:半径为1的半圆以及高为1的矩形;左视图:半径为1的圆以及高为1的矩形;俯视图:半径为1的圆.求此图形的体积.
答案:
解答:根据题意,该图形为圆柱和一个的球的组合体,
球体积应为,
圆柱体积,
则图形的体积是:.
解析:分析:由已知中的三视图,可以判断出该几何体的形状为:下部是底面半径为1,高为1的圆柱,上部为半径为1的球,组成的组合体,代入圆柱体积公式和球的体积公式,即可得到答案.
23.下面的图形是一个物体的三视图,请画出这个物体的形状.
答案:解答:如图:
解析:分析:由立体图形的三视图可得立体图形有3列,且第一列是前后两个立方体,且后面一个上面有一个立方体,第二、三列是一个立方体,进而画出图形.
24.如图是由几个小正方体所搭成的几何体上面看到的图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出从正面、左面可以看到的图形.
答案:解答:作图如下:
解析:分析:由已知条件可知,主视图有3列,每列小正方数形数目分别为2,3,4;左视图有2列,每列小正方形数目分别为4,2.据此可画出图形.
25.如图是由几个小正方体所搭成的几何体上面看到的图形,小正方形中的数字表示在该位置的小正方体的个数,请你画出从正面、左面可以看到的图形.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
答案:最多需要17个小正方体,最少需要11个小正方体.
解答:搭这样的几何体最少需要8+2+1=11个小正方体,
最多需要8+6+3=17个小正方体;
故最多需要17个小正方体,最少需要11个小正方体.
解析:分析:易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 14 页) 版权所有@21世纪教育网
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
