2025届黑龙江省哈尔滨师范大学附属中学高三下学期第四次模拟考试物理试题(PDF版、含答案)
文档属性
| 名称 | 2025届黑龙江省哈尔滨师范大学附属中学高三下学期第四次模拟考试物理试题(PDF版、含答案) |  | |
| 格式 | |||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-05 10:13:32 | ||
图片预览


文档简介
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
1.D
A.在研究机器狗的爬行动作时,要考虑大小和形状,则不能将它视为质点,故 A 错误;
B.机器狗驮着重物运动,以机器狗为参考系,重物是静止的,故 B 错误;
v s= = 5km/h
率
C.从山脚的红门到山顶的路程约为10公里,用了两个小时,由 t ,则机器狗的平均速率大小约为5km/h,
因位移的大小未知,则无法求出平均速度的大小,故 C 错误;
v x=
D.机器狗用了两个小时比普通人登山所用时间缩短了一半,由 t 可知机器狗的平均速度大小是普通人的两倍,
故 D 正确。
故选 D。
2.C
2 2
小明从最低点以大小相等的速度 v 做圆周运动,由牛顿第二定律可知 T-mg=m ,变形可得 T=mg+m ,抓住 A
v
点时的运动半径 l 较大,则绳的拉力较小,故 A 错误;圆周运动在最低点的角速度为 ω= l,因抓 A 点的半径 l 较大,
v2
则角速度较小,故 B 错误;圆周运动在最低点的向心加速度为 an= l ,因抓 A 点的半径 l 较大,则向心加速度较小,
2
故 C 1 正确;设荡起的最大高度差为 h,由动能定理可知-mgh=0- mv22 ,可得 h=2 ,则无论抓 A 点或 B 点,最终
能荡起的最大高度差相同,结合题干可知,抓住 A 点时,最终能荡到的最大高度小,故 D 错误。
3.B
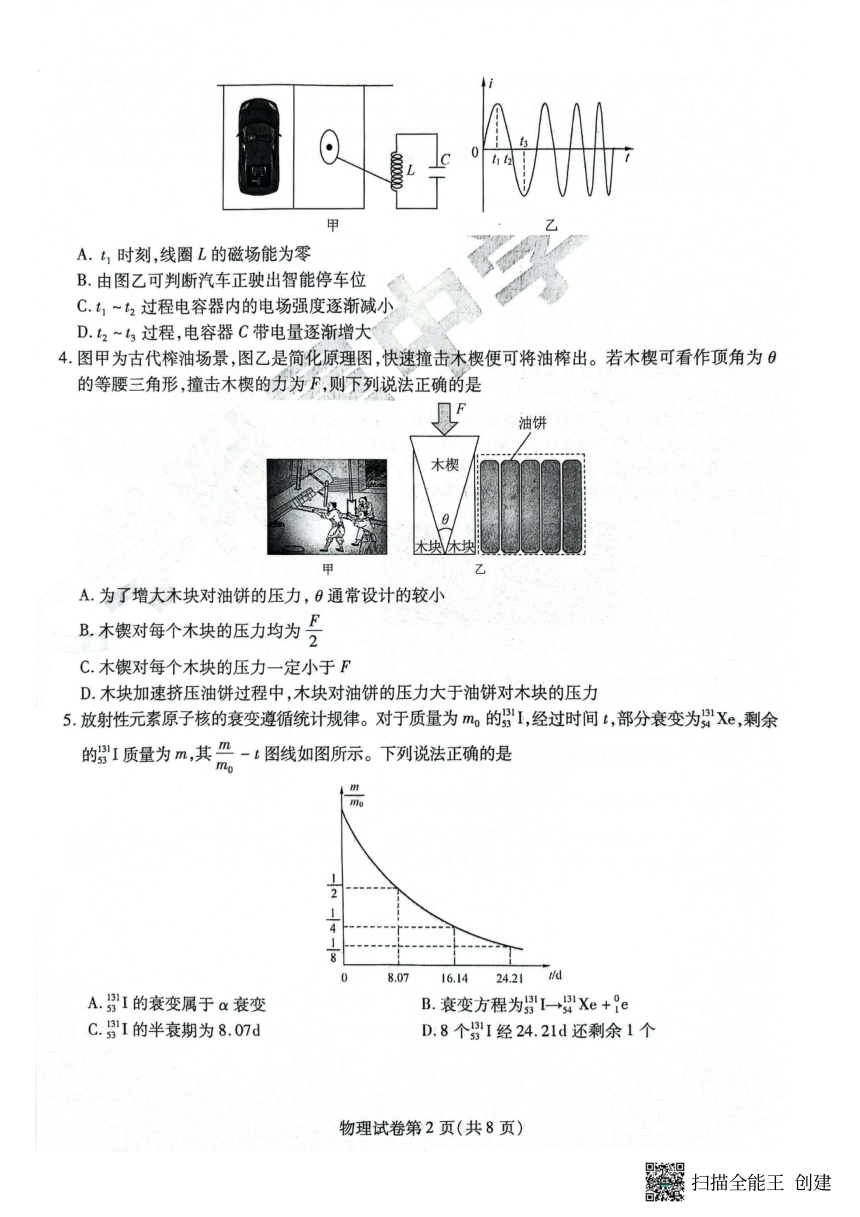
A.由乙图可知, t1 时刻电流最大,此时电容器中电荷量为零,电场能最小,磁场能最大,故 A 错误;
B.由图乙可知,振荡电路的周期变小,根据T = 2p LC
可知线圈自感系数变小,则汽车正驶离智能停车位,故 B 正确;
C.在乙图中,t1~t2过程中,电流逐渐减小,电容器正在充电,电容器内电场强度逐渐增大,故 C 不正确;
D t ~ t. 2 3过程,电流逐渐增大,电场能逐渐转化为磁场能,电容器处于放电过程,电容器带电量逐渐减小,故 D
错误。
故选 B。
4.A
F ' F=
2sin q
AB.将力 F 沿垂直侧面方向分解可知 2
F '' F ' cos q F= =
2 2 tan q
木楔对油饼的压力为 2
F
可知为了增大木块对油饼的压力,q 通常设计得较小,木锲对每个木块的压力大于 2 ,选项 A 正确,B 错误;
C.根据力的合成和分解,选项 C 错误;
D.木块对油饼的压力与油饼对木块的压力是相互作用力,总是等大反向,可知木块加速挤压油饼过程中,木块对
油饼的压力大小等于油饼对木块的压力大小,选项 D 错误。
故选 A。
5.C
131 131Xe 131 131 0AB.衰变过程中电荷数和质量数守恒,故 53I衰变为 54 的衰变方程为 53I 54 Xe + -1e
该衰变属于 β 衰变,故 AB 错误;
1
m
- t
C.由 m
131
0 图线可知, 53I的半衰期为 8.07d,故 C 正确;
D.放射性元素原子核的衰变遵循统计规律,对少数原子核不适用,故 D 错误。
故选 C。
6.B
z = -cos 2π t B ÷cm = -cos 200πt cm
A.由图乙可知周期T = 0.01s,所以,图中 B 点振动方程为 è T
故 A 错误;
l
= 0.25cm
B.实线圆、虚线圆分别表示 t = 0时刻相邻的波峰和波谷,由图甲可知 2
v l= = 0.5m/s
则波在水中的传播速度 T
故 B 正确;
2 2
OC 2 2= 2 ÷÷
+ 2 ÷÷
cm =1cm
C.根据题意可知 O 处此时处于波峰位置,且 è è
-2
t Dr (1- 0.5) 10= = s = 0.01s
实线圆传递到 C 点的时间 v 0.5
故 C 错误;
D.C 点第 10 次到达波峰的时刻 t = t + 9T = 0.1s,故 D 错误。
故选 B。
7.C
A r r.设两星球的轨道半径分别为 P 、 Q,由题意可知
rP + rQ = L1
rP - rQ = L2
解得
r L1 + L2P = 2
r L= 1 - L2Q 2
整理得
rP L1 + L= 2
rQ L1 - L2
故 A 错误;
B.星球 P、Q 环绕连线上的点做匀速圆周运动,则星球 P、Q 的角速度相等,又星球 P、Q 之间的万有引力提供向
心力,所以星球 P、Q 的向心力大小相等,则
mPr
2
Pw = mQrQw
2
因为
rP > rQ
所以
2
mP < mQ
故 B 错误;
C.由以上分析可知 P、Q 的线速度分别为
vP = wrP
vQ = wrQ
P、Q 的线速度之和为
Dv1 = vP + vQ = wL1
P、Q 的线速度之差为
Dv2 = vP - vQ = wL2
Dv1 L= 1
得 Dv2 L2
故 C 正确;
D.由牛顿第二定律对星体 P 有
m
G P
mQ 2
L2
= mPrPw
1
m r w
2L2
Q =
P 1
G
同理对 Q 有
m
G P
mQ
2 = m r w
2
L Q Q1
则
r w 2L2
m = Q 1P G
P、Q 质量之和为
2
m m m w L
3
D 1 = P + Q =
1
G
P、Q 质量之差为
w 2L2L
Dm2 = mP - mQ = 1 2G
解得
Dm1 L= 1
Dm2 L2
故 D 不正确。
故选 C。
8.BD
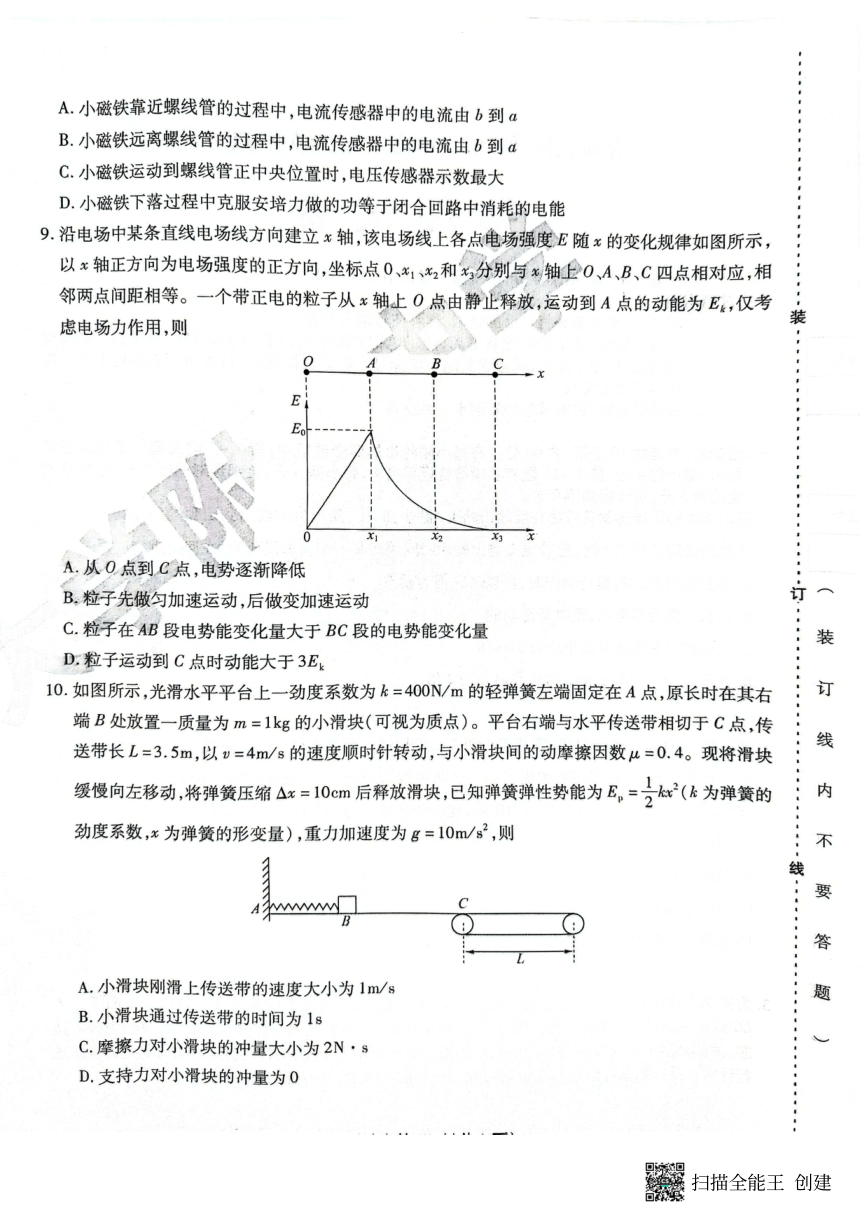
AB.小磁铁下端是 S 极,在 S 极靠近螺线管的过程中,磁通量增加,根据楞次定律结合安培定则,可知电流传感
器中的电流由 a 到 b,小磁铁远离螺线管的过程中,电流传感器中的电流由 b 到 a,故 AB 正确;
C.小磁铁运动到中央位置时,线圈中磁通量最大,磁通量的变化率为零,因此电压传感器示数为零,故 C 错误;
D.感应电流的产生,正是克服安培力做功的结果,克服安培力做了多少功,就有多少的其他形式的能转化为电能,
故 D 正确。
3
故选 BD。
9.AC
A.从 O 点到 C 点,电场强度方向保持不变,由于开始场强方向沿 x 轴正方向,所以沿电场线方向电势逐渐降低,
则从 O 点到 C 点,电势逐渐降低。故 A 正确;
B.由图像可知场强先增大后减小,则电场力也是先增大后减小,所以粒子的加速度先增大后减小,一直做变加速
运动。故 B 错误;
C.粒子在 AB 段图像的面积大于 BC 段图像的面积,则
U AB > UBC
所以粒子在 AB 段电势能减少量大于 BC 段电势能减少量。故 C 正确;
D.由图像可知图像的面积表示电势差,则有
UOC < 3UOA
由动能定理有
qUOA = Ek , qUOC = EkC
可得
EkC 3Ek
所以粒子运动到 C 点时动能小于 3Ek。故 D 错误。
故选 AC。
10.BC
A.设小滑块离开弹簧时的速度为 v0 ,由机械能守恒定律得
1 k(Δx)2 1= mv2
2 2 0
解得
v0 = 2m / s
故 A 错误;
B.设经时间 t1 ,小滑块达到与传送带共速,则由动量定理和动能定理得
mmgt1 = mv - mv0
mmgx 11 = mv
2 1- mv2
2 2 0
解得
t1 = 0.5s, x1 = 1.5m
小滑块匀速通过传送带的时间为
t L - x12 = = 0.5sv
则小滑块通过传送带的时间为
t = t1 + t2 =1s
故 B 错误;
C.传送带摩擦力对小滑块的冲量为
4
I1 = mmgt1 = 2N ×s
故 C 正确;
D.传送带支持力对小滑块的冲量为
I2 = FN t1 + t2 = mg t1 + t2 =10N ×s
故 D 错误。
故选 BC。
b
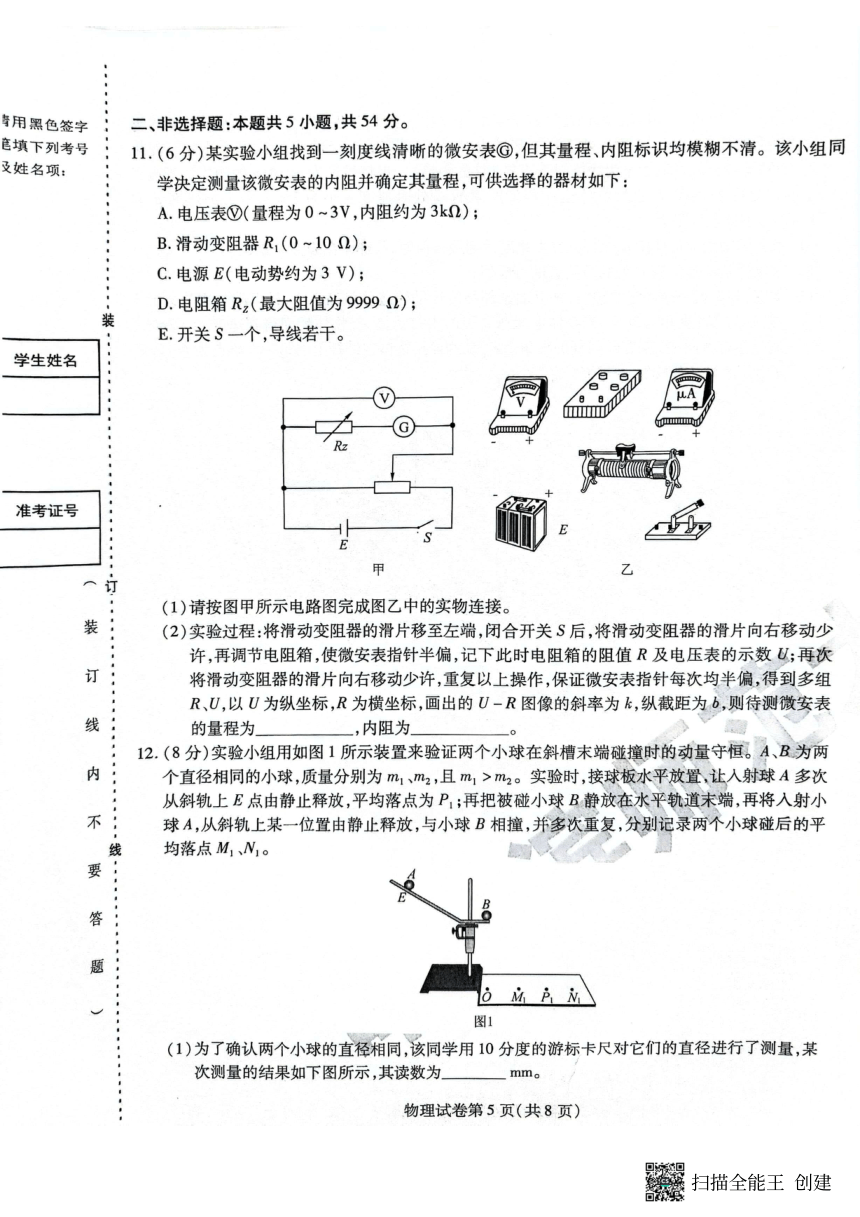
11. (1)图见解析 (2)2k k
(1)实物连接如图所示。
Ig IgRg Ig IgRg b
(2)根据部分电路欧姆定律有 U= 2 R+ 2 ,则有 k= 2,b= 2 ,解得 Ig=2k,Rg=k。
12.[答案](1)10.5 (2)AD
(3)m1x2=m1x1+m2x3
(4) 1 = 1 + 2
2 3 1
(2)题图 1 中实验是利用平抛运动的水平位移来表示小球在斜槽末端的速度,斜槽末端必须要调成水平,以保证小球
离开斜槽后做平抛运动,A 正确;斜槽倾斜部分没必要必须光滑,只要小球 A 每次均从 E 点静止释放,即可保证到
达斜槽末端时的速度相同,故 B 错误,D 正确;小球从斜槽末端飞出后做平抛运动,竖直方向上,小球下落的高度
1
相等,由 h= 22gt 可知小球在空中运动的时间相等,由 x=vt 可知小球水平位移之比等于小球做平抛运动的初速度之
比,即实验不需要测出斜槽末端距地面的高度,故 C 错误。
(3) 2设小球在空中运动的时间为 t0,根据(2)中分析可知,与 B 球碰撞前瞬间,小球 A 的速度为 v0= ,碰撞后瞬间0
1 3
小球 A、B 的速度分别为 vA= ,vB= ,若两球碰撞时动量守恒,则满足的表达式为 m1v0=m1vA+m2vB,整理得0 0
m1x2=m1x1+m2x3。
(4)设题图 2 中斜槽末端到接球板的距离为 x,小球从斜槽末端飞出时的初速度为 v,小球从斜槽末端飞出后做平抛
x 1 g
运动,则小球在空中飞行的时间为 t=v,下落距离为 y= gt
2
2 ,联立解得 v=x 2y,已知 vB>v0>vA,则碰撞前瞬间小
球 A 的速度为 v0=x 2 ,碰撞后瞬间小球 A、B 的速度分别为 vA=x 2 ,vB=x 2 ,若两球碰撞时动量守恒,2 3 1
1 2
则满足的表达式为 m v =m v +m v ,整理得 = 11 0 1 A 2 B + 。2 3 1
13.10 分
由等压变化可知
5
V0 V0 + DV= (2 分)
T0 2T0
DV = pR2h(1 分)
V
解得 h = 02 (1 分)pR
由几何关系可知,入射角等压 2 倍折射角 (1 分)
n sin 2 = (1 分)
sin
解得 = 30
∴气缸上升高度为 R(1- sin 60 ) (1 分)
由等压变化可知
V V +pR20 0 R(1- sin 60 )= (2 分)
T0 T
T 2V0 + (2 - 3)pR
3
解得 = T0 (1 分)2V0
14.(12 分)
v 2eU= 00
【答案】(1) m
B 1 2mU
p + 8 L m
= 0
(2) L e 2 2eU; 0
U 92 = U
(3) 16
0
eU 1 20 = mv0
【详解】(1)电子穿过加速电场,有 2 (2 分)
v 2eU00 =
解得 m (1 分)
tan 4L 4= =
(2)设ON 与竖直方向的夹角为 ,则有 3L 3 (1 分)
= 53o解得
2
ev B m v= 00
电子在磁场中运动时,由洛伦兹力提供向心力,有 R1 (1 分)
o
由几何关系可知,电子在磁场中的运动轨迹对应的圆心角为90 ,轨道半径R1 = R = L(1 分)
B mv 1 2mU= 0 = 0
解得 eR1 L e
6
T 2p R= 1 = 2p L m
v 2eU
电子在磁场中运动的周期 0 0 (1 分)
90ot1 = o T
p L m
=
360 2 2eU
电子在磁场中运动的时间 0 (1 分)
s 4L= - R = 4L
电子射出磁场后,继续运动了 sin (1 分)
t s m2 = = 4Lv 2eU
射到 N 点,电子射出磁场后,继续运动了 0 0 (1 分)
p + 8
t t L m= 1 + t2 =
故电子从 P 点运动到 N 2 2eU点所用的时间 0 (2 分)
15 2(18 分)【答案】(1)15m/s ;2.4m S = 4.8 +10n m S = 5.2 +10n m;(2) AC 或 AC (n=0,1,2,3…)(3)θ=60°
LGEmin=1.2m
【详解】(1)当物体在 A 处时加速度最大,由牛顿第二定律
Fm - mg = mam (1 分)
a Fm - mg 100 - 40m = = m/s
2 =15m/s2
得 m 4 (1 分)
当加速度 a=0,即 F=mg(1 分)时,速度达到最大值。由 F-y 图线可知
0 -100 F -100
=
4 y (1 分)
代入 F=mg 可得 y = 2.4m(1 分)
所以,距离 A 点 2.4m 处时,速度达到最大值。
(2)对物体的运动进行分析可知,物体从 A 处出发到达最高点,再根据运动的对称性,可知物体又会下落回到 A
处,再周而复始运动下去。
设到达上边界的 B 处时物体的速度为 vB
0 + Fm 1×d - mgd = mv2B - 0
由 A 到 B 对物体列动能定理 2 2 (1 分)解得 v = 2 5m/sB ,
设物体能上升的最大高度 H,最大高度到 B 点的距离为 h2,根据竖直上抛运动特点,可知
0 - v2B = -2gh2 (1 分) h2 =1m解得
H = h + h = 5m
所以,最高处距离 A 点高 AB 2 (1 分)
2
物体从 B 到 C 做竖直上抛运动 vC - v
2
B = -2ghBC (1 分) h = 0.8m解得 BC
所以,物体从 A 到 C 之间的总路程 SAC 可能为:
S = h + h + 2nH
当物体向上经过 C 点时 AC AB BC (n=0,1,2,3…)(1 分)
SAC = 4.8 +10n m即 (n=0,1,2,3…)(1 分)
7
C SAC = 2H - h + h当物体向下经过 点时 AB BC + 2nH (n=0,1,2,3…)(1 分)
SAC = 5.2 +10n m即 (n=0,1,2,3…)(1 分)
(3)对于物体从 D 点到 G 点的运动,
x = v0cosq
1
× t + gsin30 × t 2
沿细杆方向有 2 (1 分)
y 1= v0sinq × t - gcos30 × t
2
垂直细杆方向有 2 (1 分)
令 y=0,消去 t,整理得
2v2x 0cos(q - 30
)sinq v2 sin30
+ sin(2q - 30 )
= = ×
gcos30 0 g(cos30 )2 (1 分)
所以 θ=60°(1 分)时 x 最大,且 xmax=0.8m
x h= 2 - L
而 sin30
GE
,因此 LGEmin=1.2m(1 分)
8
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
扫描全能王 创建
1.D
A.在研究机器狗的爬行动作时,要考虑大小和形状,则不能将它视为质点,故 A 错误;
B.机器狗驮着重物运动,以机器狗为参考系,重物是静止的,故 B 错误;
v s= = 5km/h
率
C.从山脚的红门到山顶的路程约为10公里,用了两个小时,由 t ,则机器狗的平均速率大小约为5km/h,
因位移的大小未知,则无法求出平均速度的大小,故 C 错误;
v x=
D.机器狗用了两个小时比普通人登山所用时间缩短了一半,由 t 可知机器狗的平均速度大小是普通人的两倍,
故 D 正确。
故选 D。
2.C
2 2
小明从最低点以大小相等的速度 v 做圆周运动,由牛顿第二定律可知 T-mg=m ,变形可得 T=mg+m ,抓住 A
v
点时的运动半径 l 较大,则绳的拉力较小,故 A 错误;圆周运动在最低点的角速度为 ω= l,因抓 A 点的半径 l 较大,
v2
则角速度较小,故 B 错误;圆周运动在最低点的向心加速度为 an= l ,因抓 A 点的半径 l 较大,则向心加速度较小,
2
故 C 1 正确;设荡起的最大高度差为 h,由动能定理可知-mgh=0- mv22 ,可得 h=2 ,则无论抓 A 点或 B 点,最终
能荡起的最大高度差相同,结合题干可知,抓住 A 点时,最终能荡到的最大高度小,故 D 错误。
3.B
A.由乙图可知, t1 时刻电流最大,此时电容器中电荷量为零,电场能最小,磁场能最大,故 A 错误;
B.由图乙可知,振荡电路的周期变小,根据T = 2p LC
可知线圈自感系数变小,则汽车正驶离智能停车位,故 B 正确;
C.在乙图中,t1~t2过程中,电流逐渐减小,电容器正在充电,电容器内电场强度逐渐增大,故 C 不正确;
D t ~ t. 2 3过程,电流逐渐增大,电场能逐渐转化为磁场能,电容器处于放电过程,电容器带电量逐渐减小,故 D
错误。
故选 B。
4.A
F ' F=
2sin q
AB.将力 F 沿垂直侧面方向分解可知 2
F '' F ' cos q F= =
2 2 tan q
木楔对油饼的压力为 2
F
可知为了增大木块对油饼的压力,q 通常设计得较小,木锲对每个木块的压力大于 2 ,选项 A 正确,B 错误;
C.根据力的合成和分解,选项 C 错误;
D.木块对油饼的压力与油饼对木块的压力是相互作用力,总是等大反向,可知木块加速挤压油饼过程中,木块对
油饼的压力大小等于油饼对木块的压力大小,选项 D 错误。
故选 A。
5.C
131 131Xe 131 131 0AB.衰变过程中电荷数和质量数守恒,故 53I衰变为 54 的衰变方程为 53I 54 Xe + -1e
该衰变属于 β 衰变,故 AB 错误;
1
m
- t
C.由 m
131
0 图线可知, 53I的半衰期为 8.07d,故 C 正确;
D.放射性元素原子核的衰变遵循统计规律,对少数原子核不适用,故 D 错误。
故选 C。
6.B
z = -cos 2π t B ÷cm = -cos 200πt cm
A.由图乙可知周期T = 0.01s,所以,图中 B 点振动方程为 è T
故 A 错误;
l
= 0.25cm
B.实线圆、虚线圆分别表示 t = 0时刻相邻的波峰和波谷,由图甲可知 2
v l= = 0.5m/s
则波在水中的传播速度 T
故 B 正确;
2 2
OC 2 2= 2 ÷÷
+ 2 ÷÷
cm =1cm
C.根据题意可知 O 处此时处于波峰位置,且 è è
-2
t Dr (1- 0.5) 10= = s = 0.01s
实线圆传递到 C 点的时间 v 0.5
故 C 错误;
D.C 点第 10 次到达波峰的时刻 t = t + 9T = 0.1s,故 D 错误。
故选 B。
7.C
A r r.设两星球的轨道半径分别为 P 、 Q,由题意可知
rP + rQ = L1
rP - rQ = L2
解得
r L1 + L2P = 2
r L= 1 - L2Q 2
整理得
rP L1 + L= 2
rQ L1 - L2
故 A 错误;
B.星球 P、Q 环绕连线上的点做匀速圆周运动,则星球 P、Q 的角速度相等,又星球 P、Q 之间的万有引力提供向
心力,所以星球 P、Q 的向心力大小相等,则
mPr
2
Pw = mQrQw
2
因为
rP > rQ
所以
2
mP < mQ
故 B 错误;
C.由以上分析可知 P、Q 的线速度分别为
vP = wrP
vQ = wrQ
P、Q 的线速度之和为
Dv1 = vP + vQ = wL1
P、Q 的线速度之差为
Dv2 = vP - vQ = wL2
Dv1 L= 1
得 Dv2 L2
故 C 正确;
D.由牛顿第二定律对星体 P 有
m
G P
mQ 2
L2
= mPrPw
1
m r w
2L2
Q =
P 1
G
同理对 Q 有
m
G P
mQ
2 = m r w
2
L Q Q1
则
r w 2L2
m = Q 1P G
P、Q 质量之和为
2
m m m w L
3
D 1 = P + Q =
1
G
P、Q 质量之差为
w 2L2L
Dm2 = mP - mQ = 1 2G
解得
Dm1 L= 1
Dm2 L2
故 D 不正确。
故选 C。
8.BD
AB.小磁铁下端是 S 极,在 S 极靠近螺线管的过程中,磁通量增加,根据楞次定律结合安培定则,可知电流传感
器中的电流由 a 到 b,小磁铁远离螺线管的过程中,电流传感器中的电流由 b 到 a,故 AB 正确;
C.小磁铁运动到中央位置时,线圈中磁通量最大,磁通量的变化率为零,因此电压传感器示数为零,故 C 错误;
D.感应电流的产生,正是克服安培力做功的结果,克服安培力做了多少功,就有多少的其他形式的能转化为电能,
故 D 正确。
3
故选 BD。
9.AC
A.从 O 点到 C 点,电场强度方向保持不变,由于开始场强方向沿 x 轴正方向,所以沿电场线方向电势逐渐降低,
则从 O 点到 C 点,电势逐渐降低。故 A 正确;
B.由图像可知场强先增大后减小,则电场力也是先增大后减小,所以粒子的加速度先增大后减小,一直做变加速
运动。故 B 错误;
C.粒子在 AB 段图像的面积大于 BC 段图像的面积,则
U AB > UBC
所以粒子在 AB 段电势能减少量大于 BC 段电势能减少量。故 C 正确;
D.由图像可知图像的面积表示电势差,则有
UOC < 3UOA
由动能定理有
qUOA = Ek , qUOC = EkC
可得
EkC 3Ek
所以粒子运动到 C 点时动能小于 3Ek。故 D 错误。
故选 AC。
10.BC
A.设小滑块离开弹簧时的速度为 v0 ,由机械能守恒定律得
1 k(Δx)2 1= mv2
2 2 0
解得
v0 = 2m / s
故 A 错误;
B.设经时间 t1 ,小滑块达到与传送带共速,则由动量定理和动能定理得
mmgt1 = mv - mv0
mmgx 11 = mv
2 1- mv2
2 2 0
解得
t1 = 0.5s, x1 = 1.5m
小滑块匀速通过传送带的时间为
t L - x12 = = 0.5sv
则小滑块通过传送带的时间为
t = t1 + t2 =1s
故 B 错误;
C.传送带摩擦力对小滑块的冲量为
4
I1 = mmgt1 = 2N ×s
故 C 正确;
D.传送带支持力对小滑块的冲量为
I2 = FN t1 + t2 = mg t1 + t2 =10N ×s
故 D 错误。
故选 BC。
b
11. (1)图见解析 (2)2k k
(1)实物连接如图所示。
Ig IgRg Ig IgRg b
(2)根据部分电路欧姆定律有 U= 2 R+ 2 ,则有 k= 2,b= 2 ,解得 Ig=2k,Rg=k。
12.[答案](1)10.5 (2)AD
(3)m1x2=m1x1+m2x3
(4) 1 = 1 + 2
2 3 1
(2)题图 1 中实验是利用平抛运动的水平位移来表示小球在斜槽末端的速度,斜槽末端必须要调成水平,以保证小球
离开斜槽后做平抛运动,A 正确;斜槽倾斜部分没必要必须光滑,只要小球 A 每次均从 E 点静止释放,即可保证到
达斜槽末端时的速度相同,故 B 错误,D 正确;小球从斜槽末端飞出后做平抛运动,竖直方向上,小球下落的高度
1
相等,由 h= 22gt 可知小球在空中运动的时间相等,由 x=vt 可知小球水平位移之比等于小球做平抛运动的初速度之
比,即实验不需要测出斜槽末端距地面的高度,故 C 错误。
(3) 2设小球在空中运动的时间为 t0,根据(2)中分析可知,与 B 球碰撞前瞬间,小球 A 的速度为 v0= ,碰撞后瞬间0
1 3
小球 A、B 的速度分别为 vA= ,vB= ,若两球碰撞时动量守恒,则满足的表达式为 m1v0=m1vA+m2vB,整理得0 0
m1x2=m1x1+m2x3。
(4)设题图 2 中斜槽末端到接球板的距离为 x,小球从斜槽末端飞出时的初速度为 v,小球从斜槽末端飞出后做平抛
x 1 g
运动,则小球在空中飞行的时间为 t=v,下落距离为 y= gt
2
2 ,联立解得 v=x 2y,已知 vB>v0>vA,则碰撞前瞬间小
球 A 的速度为 v0=x 2 ,碰撞后瞬间小球 A、B 的速度分别为 vA=x 2 ,vB=x 2 ,若两球碰撞时动量守恒,2 3 1
1 2
则满足的表达式为 m v =m v +m v ,整理得 = 11 0 1 A 2 B + 。2 3 1
13.10 分
由等压变化可知
5
V0 V0 + DV= (2 分)
T0 2T0
DV = pR2h(1 分)
V
解得 h = 02 (1 分)pR
由几何关系可知,入射角等压 2 倍折射角 (1 分)
n sin 2 = (1 分)
sin
解得 = 30
∴气缸上升高度为 R(1- sin 60 ) (1 分)
由等压变化可知
V V +pR20 0 R(1- sin 60 )= (2 分)
T0 T
T 2V0 + (2 - 3)pR
3
解得 = T0 (1 分)2V0
14.(12 分)
v 2eU= 00
【答案】(1) m
B 1 2mU
p + 8 L m
= 0
(2) L e 2 2eU; 0
U 92 = U
(3) 16
0
eU 1 20 = mv0
【详解】(1)电子穿过加速电场,有 2 (2 分)
v 2eU00 =
解得 m (1 分)
tan 4L 4= =
(2)设ON 与竖直方向的夹角为 ,则有 3L 3 (1 分)
= 53o解得
2
ev B m v= 00
电子在磁场中运动时,由洛伦兹力提供向心力,有 R1 (1 分)
o
由几何关系可知,电子在磁场中的运动轨迹对应的圆心角为90 ,轨道半径R1 = R = L(1 分)
B mv 1 2mU= 0 = 0
解得 eR1 L e
6
T 2p R= 1 = 2p L m
v 2eU
电子在磁场中运动的周期 0 0 (1 分)
90ot1 = o T
p L m
=
360 2 2eU
电子在磁场中运动的时间 0 (1 分)
s 4L= - R = 4L
电子射出磁场后,继续运动了 sin (1 分)
t s m2 = = 4Lv 2eU
射到 N 点,电子射出磁场后,继续运动了 0 0 (1 分)
p + 8
t t L m= 1 + t2 =
故电子从 P 点运动到 N 2 2eU点所用的时间 0 (2 分)
15 2(18 分)【答案】(1)15m/s ;2.4m S = 4.8 +10n m S = 5.2 +10n m;(2) AC 或 AC (n=0,1,2,3…)(3)θ=60°
LGEmin=1.2m
【详解】(1)当物体在 A 处时加速度最大,由牛顿第二定律
Fm - mg = mam (1 分)
a Fm - mg 100 - 40m = = m/s
2 =15m/s2
得 m 4 (1 分)
当加速度 a=0,即 F=mg(1 分)时,速度达到最大值。由 F-y 图线可知
0 -100 F -100
=
4 y (1 分)
代入 F=mg 可得 y = 2.4m(1 分)
所以,距离 A 点 2.4m 处时,速度达到最大值。
(2)对物体的运动进行分析可知,物体从 A 处出发到达最高点,再根据运动的对称性,可知物体又会下落回到 A
处,再周而复始运动下去。
设到达上边界的 B 处时物体的速度为 vB
0 + Fm 1×d - mgd = mv2B - 0
由 A 到 B 对物体列动能定理 2 2 (1 分)解得 v = 2 5m/sB ,
设物体能上升的最大高度 H,最大高度到 B 点的距离为 h2,根据竖直上抛运动特点,可知
0 - v2B = -2gh2 (1 分) h2 =1m解得
H = h + h = 5m
所以,最高处距离 A 点高 AB 2 (1 分)
2
物体从 B 到 C 做竖直上抛运动 vC - v
2
B = -2ghBC (1 分) h = 0.8m解得 BC
所以,物体从 A 到 C 之间的总路程 SAC 可能为:
S = h + h + 2nH
当物体向上经过 C 点时 AC AB BC (n=0,1,2,3…)(1 分)
SAC = 4.8 +10n m即 (n=0,1,2,3…)(1 分)
7
C SAC = 2H - h + h当物体向下经过 点时 AB BC + 2nH (n=0,1,2,3…)(1 分)
SAC = 5.2 +10n m即 (n=0,1,2,3…)(1 分)
(3)对于物体从 D 点到 G 点的运动,
x = v0cosq
1
× t + gsin30 × t 2
沿细杆方向有 2 (1 分)
y 1= v0sinq × t - gcos30 × t
2
垂直细杆方向有 2 (1 分)
令 y=0,消去 t,整理得
2v2x 0cos(q - 30
)sinq v2 sin30
+ sin(2q - 30 )
= = ×
gcos30 0 g(cos30 )2 (1 分)
所以 θ=60°(1 分)时 x 最大,且 xmax=0.8m
x h= 2 - L
而 sin30
GE
,因此 LGEmin=1.2m(1 分)
8
同课章节目录
