第八章统计和概率的简单应用同步强化练习(含解析)
文档属性
| 名称 | 第八章统计和概率的简单应用同步强化练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 731.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 10:04:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章统计和概率的简单应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
A.900名 B.1050名 C.600名 D.450名
2.有4万个不小于70的两位数,从中随机抽取了3000个数据,统计如下:
数据x 70≤x≤79 80≤x≤89 90≤x≤99
个数 800 1300 900
平均数 78.1 85 91.9
请根据表格中的信息,估计这4万个数据的平均数为 ( )
A.92.16 B.85.23
C.84.73 D.77.97
3.合肥市农科所在相同条件下经试验发现玉米种子的发芽率为,该市某种粮大户准备了玉米种子用来育种,他可能会损失大约( ).
A.971 B.129 C.97.1 D.29
4.一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在80%左右,则a的值约为( )
A.9 B.12 C.15 D.18
5.一个不透明的箱子里装有m个球,其中红球有5个,这些球除颜色外都相同.每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回.大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出m的值为( )
A.25 B.20 C.15 D.10
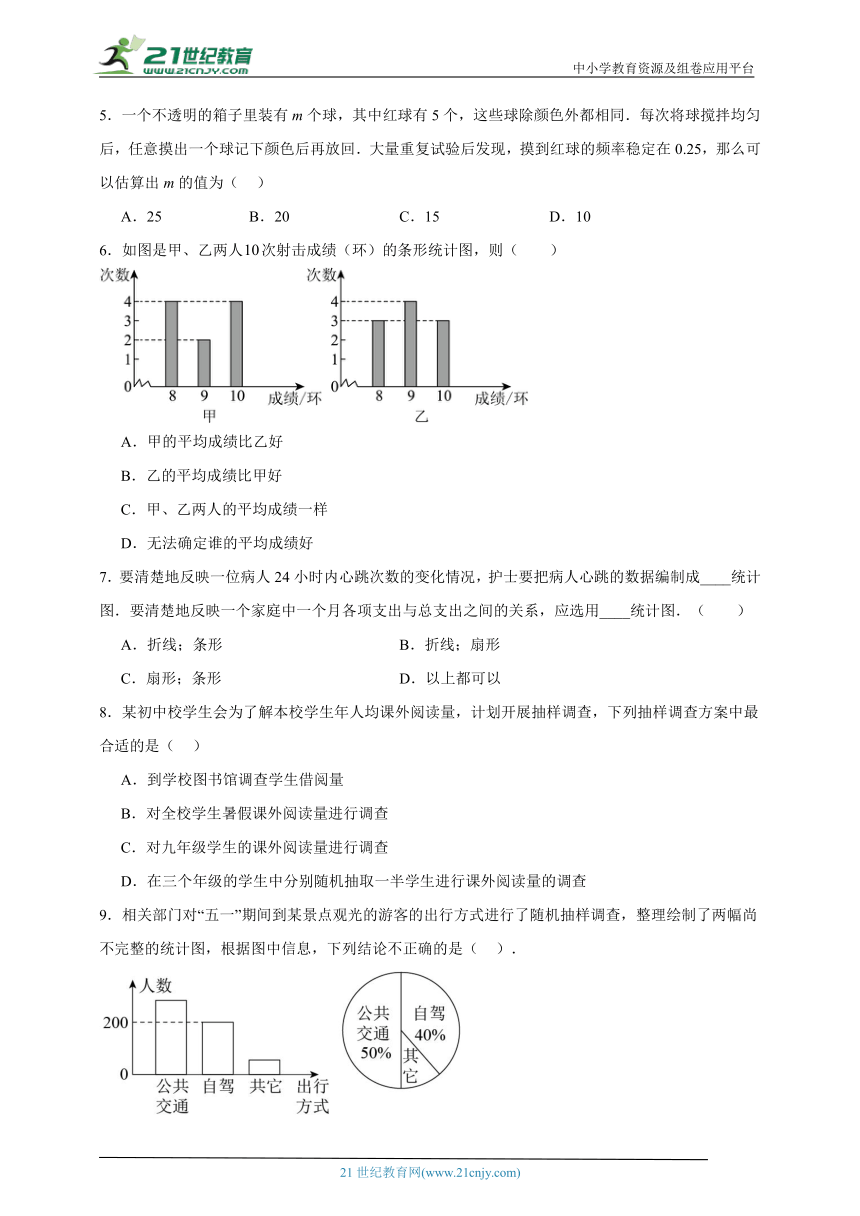
6.如图是甲、乙两人次射击成绩(环)的条形统计图,则( )
A.甲的平均成绩比乙好
B.乙的平均成绩比甲好
C.甲、乙两人的平均成绩一样
D.无法确定谁的平均成绩好
7.要清楚地反映一位病人24小时内心跳次数的变化情况,护士要把病人心跳的数据编制成____统计图.要清楚地反映一个家庭中一个月各项支出与总支出之间的关系,应选用____统计图.( )
A.折线;条形 B.折线;扇形
C.扇形;条形 D.以上都可以
8.某初中校学生会为了解本校学生年人均课外阅读量,计划开展抽样调查,下列抽样调查方案中最合适的是( )
A.到学校图书馆调查学生借阅量
B.对全校学生暑假课外阅读量进行调查
C.对九年级学生的课外阅读量进行调查
D.在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查
9.相关部门对“五一”期间到某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( ).
A.本次抽样调查的样本容量是500
B.扇形统计图中“其它”的占比为10%
C.样本中选择公共交通出行的有250人
D.若“五一”期间到该景点观光的游客有50万人,则选择自驾出行的约有25万人
10.生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) 合计
频数 1 2 3
频率 0.05 0.10 0.15 1
表中组的频率满足.
下面有四个推断:
①表中的值为20;
②表中的值可以为7;
③这天的日均可回收物回收量的中位数在组;
④这天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①② B.①③ C.②③④ D.①③④
11.中考结束后,小明想了解今年河南各普高的录取分数线,他需通过什么方法获得这些数据?( )
A.测量 B.直接观察法 C.试验 D.互联网查询
12.小杰想了解我国历年来的全国粮食总产量,他获得这些数据的最佳方式是( )
A.测量 B.直接观察 C.调查 D.查阅文献资料
二、填空题
13.6月6日是全国爱眼日,某校对七年级学生进行了视力监测,收集了部分学生的监测数据,并绘制成了频数分布直方图,从左至右每个小长方形的高的比为1∶4∶3∶2,其中第三组的频数为45,则共收集了 名学生的监测数据.
14.在一个不透明的盒子中装有黑球和白球共500个,这些球除颜色外其余均相同,将球搅匀后任意摸出一个球,记下颜色后放回,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.1,则盒子中白球有 个.
15.有两组相同的纸牌,它们的牌面数分别是,,.从每组牌中各随机摸出一张,这为一次试验.小明做了次试验后发现和为的情况出现了次,据此估计牌面数字的和是的概率是 (精确到).
16.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):若该小区有 户家庭,据此估计该小区月均用水量不超过 的家庭约有 户.
17.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命,从中随机抽取了50只灯泡进行检测,获得了它们的使用寿命(单位:小时),数据整理如下:
使用寿命
灯泡只数 5 10 12 17 6
根据以上数据,估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为 只.
三、解答题
18.下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) 50 100 150 209 250 300 350
投中次数(m) 28 60 78 104 123 152 175
投中频率(n/m) 0.56 0.60 0.49
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
19.下表是某口罩生产厂对一批N95口罩质量检测的情况:
抽取口罩数 200 500 1000 1500 2000 3000
合格品数 188 471 946 1426 1898 2850
合格品频率 (精确到0.001) 0.940 0.942 0.946 0.951 a b
(1)a=__________,b=__________;
(2)从这批口罩中任意抽取一个是合格品的概率估计值是多少?(精确到0.01)
(3)若要生产380000个合格的N95口罩,该厂估计要生产多少个N95口罩?
20.某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计人,良好漏统计人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 调整前人数 调整后人数
优秀
良好
及格
不及格
合计
学生体能测试成绩各等次人数统计图
21.某校七年级共10个班,为了了解本年级学生一周中收看电视节目所用的时间,小亮利用放学时在校门口调查了他认识的60名七年级同学.
(1)小亮的调查是抽样调查吗?
(2)如果是抽样调查,指出调查的总体、个体和样本容量.
(3)根据他调查的结果,能反映七年级同学平均一周收看电视的时间吗?为什么?
22.今年,苏州市政府的一项实事工程就是由政府投入1000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况 均不改造 改造水龙头 改造马桶
1个 2个 3个 4个 1个 2个
户数 20 31 28 21 12 69 2
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有 ___________户;
(2)改造后一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
23.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
24.如图所示,图①表示的是某教育网站一周内连续7天日访问总量的情况,图②表示的是学生日访问量占日访问总量的百分比情况,观察图①、②,解答下列问题:
(1)若这7天的日访问总量一共约为10万人次,求星期三的日访问总量;
(2)求星期日学生日访问总量;
(3)请写出一条从统计图中得到的信息.
《第八章统计和概率的简单应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B C B D D D
题号 11 12
答案 D D
1.D
【分析】用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
【详解】解:100名学生中“使用电子鞭炮”的学生有人,“使用电子鞭炮”的百分比为:
全校“使用电子鞭炮”的学生有:人.
故选D.
【点睛】本题考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
2.B
【分析】先计算这3000个数的平均数,即样本的平均数,再利用样本的平均数去估计总体平均数,即可解答
【详解】这3000个数据的平均数为 =85.23.由用样本的平均数去估计总体的平均数,可知,这4万个数据的平均数约为85.23.故选B.
【点睛】此题考查加权平均数,用样本估计总体,解题关键在于先算出平均数
3.D
【分析】本题考查有样本估计总体,解题的关键是明确题意,注意求得是不能发芽的种子数,根据玉米种子的发芽率为,可估计斤玉米种子中不能发芽的大约有多少千克.
【详解】解:由题意可得,斤玉米种子中不能发芽的大约有:(),
故选:D.
4.B
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从摸到白球的频率稳定在80%左右得到比例关系,列出方程求解即可.
【详解】解:由题意可得,×100%=80%,
解得,a=12.
故选:B.
【点睛】本题利用了用大量试验得到的频率可以估计事件的概率.关键是根据红球的频率得到相应的等量关系.
5.B
【分析】用红球的数量除以红球的频率即可.
【详解】解:(个,
所以可以估算出的值为20,
故选:B.
【点睛】本题考查利用频率估计概率,解题的关键是掌握在大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
6.C
【分析】本题考查的知识点是利用平均数做决策、由条形统计图推断结论,解题关键是结合条形统计图计算甲、乙对应的平均数.
先根据条形统计图计算甲、乙对应的平均数,比较后即可求解.
【详解】解:依题得:甲的平均成绩为,
乙的平均成绩为,
,
甲、乙两人的平均成绩一样,
故选:.
7.B
【分析】本题考查了条形统计图、折线统计图、扇形统计图,熟悉各自的特点是解答本题的关键.统计表是用线条来表现统计资料的表格;条形统计图的特点是能很容易看出数量的多少;折线统计图特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图的特点是能反映部分与整体的关系,由此根据情况选择即可.
【详解】解:要清楚地反映一位病人24小时内心跳次数的变化情况,护士要把病人心跳的数据编制成折线统计图.
要清楚地反映一个家庭中一个月各项支出与总支出之间的关系,应选用扇形统计图,
故选:B.
8.D
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】解:A、调查对象不具有代表性,故A错误;
B、调查对象不具有代表性,故B错误;
C、调查对象不具广泛性和代表性,故C错误;
D、在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查,调查对象比较合适,故此选项正确;
故选D.
【点睛】此题主要考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
9.D
【分析】根据统计图中的信息,求出总人数,m,再求出样本中选择公共交通出行的人,再求出选择公共交通出行的约有的人数,“五一”期间到该景点观光的游客有50万人,选择自驾方式出行约有的人数,可得结论.
【详解】样本容量
m= 1- 50%- 40%= 10%,
样本中选择公共交通出行的约有500×50%= 250人
若“五一”期间到该景点观光的游客有50万人,则选择自驾方式出行的约为50 × 40%= 20万人
故A,B,C正确,
故选:D.
【点睛】本题考查条形统计图,总体,个体,样本容量,样本估计总体的思想等知识,解题的关键是读懂图象信息,属于中考常考题型.
10.D
【分析】①根据数据总和=频数÷频率,列式计算即可得出m的值;
②根据的频率a满足,可求出该范围的频数,进一步得出b的值的范围,从而求解;
③根据中位数的定义即可求解;
④根据加权平均数的计算公式即可求解.
【详解】解:①日均可回收物回收量(千吨)为时,频数为1,频率为0.05,所以总数m=,推断合理;
②20×0.2=4,20×0.3=6,
1+2+6+3=12,故表中b的值可以为7,是不合理的推断;
③1+2+6=9,故这m天的日均可回收物回收量的中位数在组,是合理推断;
④(1+5)÷2=3,0.05+0.10=0.15,这天的日均可回收物回收量的平均数不低于3,是合理推断.
故选:D
【点睛】本题考查频数(率)分布表,从表中获取数量及数量之间的关系是解题问题的关键.
11.D
【分析】本题主要考查了数据收集与整理的方法,根据考查的目的,结合实际情况综合进行判断即可,根据考查的目的和实际的情况抽取适当的方法进行考查是解决问题的关键.
【详解】解:∵考查的目的为“今年河南各普高的录取分数线”,可以上网查阅或查阅文献资料即可,
∴选项D比较符合题意,
故选:D.
12.D
【分析】本题考查了数据的收集,根据数据的特点即可判断求解,掌握数据收集的方法是解题的关键.
【详解】解:他获得这些数据的最佳方式是查阅文献资料,
故选:.
13.150
【解析】略
14.50
【分析】大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】解:因为通过大量重复摸球试验后,发现摸到白球的频率稳定在0.1,
所以摸到白球的概率约为0.1,
所以白球有500×0.1=50,
故答案为:50.
【点睛】本题考查了利用频率估计概率,解决本题的关键是掌握频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
15.
【分析】本题主要考查了利用频率估计概率,概率公式等知识点,掌握概率的计算方法及相关知识是解题的关键.
根据题意结合概率的计算方法进行解答即可.
【详解】解:根据题意得:
,
故答案为:.
16.560
【分析】根据用水量在的频率和频数,求出调查的总人数,根据由频数=数据总数×频率计算出用水量在的频数,求出用水量在的频数,求得参与调查的100户家庭中用水量不超过的频率,进而求出在800户家庭中,月均用水量不超过的家庭人数.
【详解】解:根据题意得调查的总人数为:(户),
则的频数是(户),
的频数是:(户),
∴参与调查的100户家庭中用水量不超过的有户,
频率为,
∴在800户家庭中,月均用水量不超过10m3的家庭约有(户).
【点睛】本题考查频率、频数分布表、用样本估计总体,理解题意,正确求解是解答的关键.
17.460
【详解】估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为(只).
18.(1)0.52,0.50,0.51,0.58;(2)P≈0.5;
【详解】试题分析:(1)用投中的次数除以投篮的次数即可得出答案;
(2)计算出所有投篮的次数,再计算出总的命中数,继而可估计出这名球员投篮一次,投中的概率.
试题解析:(1)根据题意得:
78÷150=0.52;
104÷209≈0.50;
152÷300≈0.51;
175÷350≈0.58;
填表如下:
投篮次数(n) 50 100 150 209 250 300 350
投中次数(m) 28 60 78 104 123 152 175
投中频率(n/m) 0.56 0.60 0.52 0.50 0.49 0.51 0.58
故答案为0.52,0.50,0.51,0.58;
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720,
故这名球员投篮一次,投中的概率约为:≈0.5.
故答案为0.5
19.(1)0.949,0.950;(2)0.95;(3)400000
【分析】(1)根据表中数据计算即可;
(2)由表中数据可判断频率在0.95左右摆动,从而利于频率估计概率可判断任意抽取一只口罩是合格品的概率为0.95;
(3)用样本数据估计总体即可.
【详解】解:(1)1898÷2000=0.949,2850÷3000=0.950;
故答案为:0.949,0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
(3).
答:该厂估计要生产400000个N95口罩.
【点睛】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
20.(1)详见解析;(2)详见解析;(3)360.
【分析】(1)根据题和统计表给出的数据即可填写统计表;
(2)根据调整后统计表的数据即可补全条形统计图;
(3)根据抽取的学生中体能测试的优秀率为24%;从而求出该校体能测试为“优秀”的人数.
【详解】解:(1)解:填写的统计表如图1所示:
(2)解:补全的条形统计图如图2所示:
(3)解:抽取的学生中体能测试的优秀率为:12÷50=24%;
∴该校体能测试为“优秀”的人数为1500×24%=360(人)
21.(1)是抽样调查;(2)调查的总体是该校七年级共10个班学生一周中收看电视节目所用的时间,个体是每个同学一周中收看电视节目所用的时间,样本容量是60;(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面
【分析】(1)根据调查的人数与调查的总体进行比较即可得出答案;
(2)总体是指调查对象的全体,个体是总体中的每一个调查的对象,样本容量则是指样本中个体的数量,据此进一步得出答案即可;
(3)根据题意,结合调查的情况进一步分析判断即可.
【详解】(1)小亮的调查是抽样调查;
(2)调查的总体是该校七年级共10个班学生一周中收看电视节目所用的时间;
个体是每个同学一周中收看电视节目所用的时间;
样本容量是60;
(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面.
【点睛】本题主要考查了抽样调查的运用,熟练掌握相关概念是解题关键.
22.(1)1000
(2)20850
(3)63户
【分析】(1)首先计算样本中需要对水龙头、马桶进行改造的家庭所占的百分比,然后根据样本进一步估计总体;
(2)首先计算100户共节约用水量,再进一步计算该社区共节约用水量;
(3)根据题意设未知数,列方程即可求解:改造水龙头数改造马桶数既要改造水龙头又要改造马桶数.
【详解】(1)解:由题意得:估计该社区1200户家庭中需要对水龙头、马桶进行改造的家庭户数为
(户,
故答案为:1000;
(2)解:抽样的120户家庭一年共可节约用水:
(吨.
所以,该社区一年共可节约用水的吨数为(吨.
(3)解:设既要改造水龙头又要改造马桶的家庭共有户,则只改造水龙头不改造马桶的家庭共有户,只改造马桶不改造水龙头的家庭共有户,根据题意列方程,得
,解得,.
所以,既要改造水龙头又要改造马桶的家庭共有63户.
也可以从另一角度考虑,从表中数据可以看出,在这120户中,改造水龙头和改造马桶的户数之和为(户.
由于只有100户需要对水龙头、马桶进行改造,所以多出的就是既要改造水龙头又要改造马桶的家庭.因此,此类家庭的人数为(户.
答:既要改造水龙头又要改造马桶的家庭大约有63户.
【点睛】本题考查获取信息(读表)及综合运用数学知识分析问题、解决问题的能力,用样本估计总体,平均数,一元一次方程的应用,有理数的加法运算,熟练掌握知识点是解题的关键.
23.(1)样本容量为50;(2)平均数为14(岁);中位数为14(岁),众数为15岁;(3)估计该校年龄在15岁及以上的学生人数为720人.
【分析】(1)由12岁的人数除以所占百分比可得样本容量;
(2)先求出14、16岁的人数,再根据平均数、众数和中位数的定义求解可得;
(3)用总人数乘以样本中15、16岁的人数所占比例可得.
【详解】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)0.5万人次.
(2)3×30%=0.9万人次.
(3)某教育网站一周内星期日的日访问总量最大.
【分析】(1)由这7天的日访问总量一共约为10万人次,结合条形统计图可得除星期三以外的其它天的日访问总量分别为:0.5万人次,1万人次,1万人次,1.5万人次,2.5万人次,3万人次,继而求得星期三的日访问总量.
(2)由星期日的日访问总量为3万人次,结合扇形统计图可得星期日学生日访问总量占日访问总量的百分比为30%,继而求得星期日学生日访问总量.
(3)结合图可得某教育网站一周内星期日的日访问总量最大(答案不唯一).
【详解】解:(1)∵这7天的日访问总量一共约为10万人次,除星期三以外的其它天的日访问总量分别为:0.5万人次,1万人次,1万人次,1.5万人次,2.5万人次,3万人次,
∴星期三的日访问总量为:10﹣0.5﹣1﹣1﹣1.5﹣2.5﹣3=0.5(万人次).
(2)∵星期日的日访问总量为3万人次,星期日学生日访问总量占日访问总量的百分比为30%,
∴星期日学生日访问总量为:3×30%=0.9(万人次).
(3)某教育网站一周内星期日的日访问总量最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章统计和概率的简单应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
A.900名 B.1050名 C.600名 D.450名
2.有4万个不小于70的两位数,从中随机抽取了3000个数据,统计如下:
数据x 70≤x≤79 80≤x≤89 90≤x≤99
个数 800 1300 900
平均数 78.1 85 91.9
请根据表格中的信息,估计这4万个数据的平均数为 ( )
A.92.16 B.85.23
C.84.73 D.77.97
3.合肥市农科所在相同条件下经试验发现玉米种子的发芽率为,该市某种粮大户准备了玉米种子用来育种,他可能会损失大约( ).
A.971 B.129 C.97.1 D.29
4.一个盒子中装有a个白球和3个红球(除颜色外完全相同),若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到白球的频率稳定在80%左右,则a的值约为( )
A.9 B.12 C.15 D.18
5.一个不透明的箱子里装有m个球,其中红球有5个,这些球除颜色外都相同.每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回.大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出m的值为( )
A.25 B.20 C.15 D.10
6.如图是甲、乙两人次射击成绩(环)的条形统计图,则( )
A.甲的平均成绩比乙好
B.乙的平均成绩比甲好
C.甲、乙两人的平均成绩一样
D.无法确定谁的平均成绩好
7.要清楚地反映一位病人24小时内心跳次数的变化情况,护士要把病人心跳的数据编制成____统计图.要清楚地反映一个家庭中一个月各项支出与总支出之间的关系,应选用____统计图.( )
A.折线;条形 B.折线;扇形
C.扇形;条形 D.以上都可以
8.某初中校学生会为了解本校学生年人均课外阅读量,计划开展抽样调查,下列抽样调查方案中最合适的是( )
A.到学校图书馆调查学生借阅量
B.对全校学生暑假课外阅读量进行调查
C.对九年级学生的课外阅读量进行调查
D.在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查
9.相关部门对“五一”期间到某景点观光的游客的出行方式进行了随机抽样调查,整理绘制了两幅尚不完整的统计图,根据图中信息,下列结论不正确的是( ).
A.本次抽样调查的样本容量是500
B.扇形统计图中“其它”的占比为10%
C.样本中选择公共交通出行的有250人
D.若“五一”期间到该景点观光的游客有50万人,则选择自驾出行的约有25万人
10.生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) 合计
频数 1 2 3
频率 0.05 0.10 0.15 1
表中组的频率满足.
下面有四个推断:
①表中的值为20;
②表中的值可以为7;
③这天的日均可回收物回收量的中位数在组;
④这天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①② B.①③ C.②③④ D.①③④
11.中考结束后,小明想了解今年河南各普高的录取分数线,他需通过什么方法获得这些数据?( )
A.测量 B.直接观察法 C.试验 D.互联网查询
12.小杰想了解我国历年来的全国粮食总产量,他获得这些数据的最佳方式是( )
A.测量 B.直接观察 C.调查 D.查阅文献资料
二、填空题
13.6月6日是全国爱眼日,某校对七年级学生进行了视力监测,收集了部分学生的监测数据,并绘制成了频数分布直方图,从左至右每个小长方形的高的比为1∶4∶3∶2,其中第三组的频数为45,则共收集了 名学生的监测数据.
14.在一个不透明的盒子中装有黑球和白球共500个,这些球除颜色外其余均相同,将球搅匀后任意摸出一个球,记下颜色后放回,通过大量重复摸球试验后,发现摸到白球的频率稳定在0.1,则盒子中白球有 个.
15.有两组相同的纸牌,它们的牌面数分别是,,.从每组牌中各随机摸出一张,这为一次试验.小明做了次试验后发现和为的情况出现了次,据此估计牌面数字的和是的概率是 (精确到).
16.七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):若该小区有 户家庭,据此估计该小区月均用水量不超过 的家庭约有 户.
17.某厂生产了1000只灯泡.为了解这1000只灯泡的使用寿命,从中随机抽取了50只灯泡进行检测,获得了它们的使用寿命(单位:小时),数据整理如下:
使用寿命
灯泡只数 5 10 12 17 6
根据以上数据,估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为 只.
三、解答题
18.下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) 50 100 150 209 250 300 350
投中次数(m) 28 60 78 104 123 152 175
投中频率(n/m) 0.56 0.60 0.49
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
19.下表是某口罩生产厂对一批N95口罩质量检测的情况:
抽取口罩数 200 500 1000 1500 2000 3000
合格品数 188 471 946 1426 1898 2850
合格品频率 (精确到0.001) 0.940 0.942 0.946 0.951 a b
(1)a=__________,b=__________;
(2)从这批口罩中任意抽取一个是合格品的概率估计值是多少?(精确到0.01)
(3)若要生产380000个合格的N95口罩,该厂估计要生产多少个N95口罩?
20.某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计人,良好漏统计人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 调整前人数 调整后人数
优秀
良好
及格
不及格
合计
学生体能测试成绩各等次人数统计图
21.某校七年级共10个班,为了了解本年级学生一周中收看电视节目所用的时间,小亮利用放学时在校门口调查了他认识的60名七年级同学.
(1)小亮的调查是抽样调查吗?
(2)如果是抽样调查,指出调查的总体、个体和样本容量.
(3)根据他调查的结果,能反映七年级同学平均一周收看电视的时间吗?为什么?
22.今年,苏州市政府的一项实事工程就是由政府投入1000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况 均不改造 改造水龙头 改造马桶
1个 2个 3个 4个 1个 2个
户数 20 31 28 21 12 69 2
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有 ___________户;
(2)改造后一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
23.某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
依据以上信息解答以下问题:
(1)求样本容量;
(2)直接写出样本容量的平均数,众数和中位数;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
24.如图所示,图①表示的是某教育网站一周内连续7天日访问总量的情况,图②表示的是学生日访问量占日访问总量的百分比情况,观察图①、②,解答下列问题:
(1)若这7天的日访问总量一共约为10万人次,求星期三的日访问总量;
(2)求星期日学生日访问总量;
(3)请写出一条从统计图中得到的信息.
《第八章统计和概率的简单应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B B C B D D D
题号 11 12
答案 D D
1.D
【分析】用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
【详解】解:100名学生中“使用电子鞭炮”的学生有人,“使用电子鞭炮”的百分比为:
全校“使用电子鞭炮”的学生有:人.
故选D.
【点睛】本题考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
2.B
【分析】先计算这3000个数的平均数,即样本的平均数,再利用样本的平均数去估计总体平均数,即可解答
【详解】这3000个数据的平均数为 =85.23.由用样本的平均数去估计总体的平均数,可知,这4万个数据的平均数约为85.23.故选B.
【点睛】此题考查加权平均数,用样本估计总体,解题关键在于先算出平均数
3.D
【分析】本题考查有样本估计总体,解题的关键是明确题意,注意求得是不能发芽的种子数,根据玉米种子的发芽率为,可估计斤玉米种子中不能发芽的大约有多少千克.
【详解】解:由题意可得,斤玉米种子中不能发芽的大约有:(),
故选:D.
4.B
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从摸到白球的频率稳定在80%左右得到比例关系,列出方程求解即可.
【详解】解:由题意可得,×100%=80%,
解得,a=12.
故选:B.
【点睛】本题利用了用大量试验得到的频率可以估计事件的概率.关键是根据红球的频率得到相应的等量关系.
5.B
【分析】用红球的数量除以红球的频率即可.
【详解】解:(个,
所以可以估算出的值为20,
故选:B.
【点睛】本题考查利用频率估计概率,解题的关键是掌握在大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
6.C
【分析】本题考查的知识点是利用平均数做决策、由条形统计图推断结论,解题关键是结合条形统计图计算甲、乙对应的平均数.
先根据条形统计图计算甲、乙对应的平均数,比较后即可求解.
【详解】解:依题得:甲的平均成绩为,
乙的平均成绩为,
,
甲、乙两人的平均成绩一样,
故选:.
7.B
【分析】本题考查了条形统计图、折线统计图、扇形统计图,熟悉各自的特点是解答本题的关键.统计表是用线条来表现统计资料的表格;条形统计图的特点是能很容易看出数量的多少;折线统计图特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图的特点是能反映部分与整体的关系,由此根据情况选择即可.
【详解】解:要清楚地反映一位病人24小时内心跳次数的变化情况,护士要把病人心跳的数据编制成折线统计图.
要清楚地反映一个家庭中一个月各项支出与总支出之间的关系,应选用扇形统计图,
故选:B.
8.D
【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
【详解】解:A、调查对象不具有代表性,故A错误;
B、调查对象不具有代表性,故B错误;
C、调查对象不具广泛性和代表性,故C错误;
D、在三个年级的学生中分别随机抽取一半学生进行课外阅读量的调查,调查对象比较合适,故此选项正确;
故选D.
【点睛】此题主要考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
9.D
【分析】根据统计图中的信息,求出总人数,m,再求出样本中选择公共交通出行的人,再求出选择公共交通出行的约有的人数,“五一”期间到该景点观光的游客有50万人,选择自驾方式出行约有的人数,可得结论.
【详解】样本容量
m= 1- 50%- 40%= 10%,
样本中选择公共交通出行的约有500×50%= 250人
若“五一”期间到该景点观光的游客有50万人,则选择自驾方式出行的约为50 × 40%= 20万人
故A,B,C正确,
故选:D.
【点睛】本题考查条形统计图,总体,个体,样本容量,样本估计总体的思想等知识,解题的关键是读懂图象信息,属于中考常考题型.
10.D
【分析】①根据数据总和=频数÷频率,列式计算即可得出m的值;
②根据的频率a满足,可求出该范围的频数,进一步得出b的值的范围,从而求解;
③根据中位数的定义即可求解;
④根据加权平均数的计算公式即可求解.
【详解】解:①日均可回收物回收量(千吨)为时,频数为1,频率为0.05,所以总数m=,推断合理;
②20×0.2=4,20×0.3=6,
1+2+6+3=12,故表中b的值可以为7,是不合理的推断;
③1+2+6=9,故这m天的日均可回收物回收量的中位数在组,是合理推断;
④(1+5)÷2=3,0.05+0.10=0.15,这天的日均可回收物回收量的平均数不低于3,是合理推断.
故选:D
【点睛】本题考查频数(率)分布表,从表中获取数量及数量之间的关系是解题问题的关键.
11.D
【分析】本题主要考查了数据收集与整理的方法,根据考查的目的,结合实际情况综合进行判断即可,根据考查的目的和实际的情况抽取适当的方法进行考查是解决问题的关键.
【详解】解:∵考查的目的为“今年河南各普高的录取分数线”,可以上网查阅或查阅文献资料即可,
∴选项D比较符合题意,
故选:D.
12.D
【分析】本题考查了数据的收集,根据数据的特点即可判断求解,掌握数据收集的方法是解题的关键.
【详解】解:他获得这些数据的最佳方式是查阅文献资料,
故选:.
13.150
【解析】略
14.50
【分析】大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】解:因为通过大量重复摸球试验后,发现摸到白球的频率稳定在0.1,
所以摸到白球的概率约为0.1,
所以白球有500×0.1=50,
故答案为:50.
【点睛】本题考查了利用频率估计概率,解决本题的关键是掌握频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
15.
【分析】本题主要考查了利用频率估计概率,概率公式等知识点,掌握概率的计算方法及相关知识是解题的关键.
根据题意结合概率的计算方法进行解答即可.
【详解】解:根据题意得:
,
故答案为:.
16.560
【分析】根据用水量在的频率和频数,求出调查的总人数,根据由频数=数据总数×频率计算出用水量在的频数,求出用水量在的频数,求得参与调查的100户家庭中用水量不超过的频率,进而求出在800户家庭中,月均用水量不超过的家庭人数.
【详解】解:根据题意得调查的总人数为:(户),
则的频数是(户),
的频数是:(户),
∴参与调查的100户家庭中用水量不超过的有户,
频率为,
∴在800户家庭中,月均用水量不超过10m3的家庭约有(户).
【点睛】本题考查频率、频数分布表、用样本估计总体,理解题意,正确求解是解答的关键.
17.460
【详解】估计这1000只灯泡中使用寿命不小于2200小时的灯泡的数量为(只).
18.(1)0.52,0.50,0.51,0.58;(2)P≈0.5;
【详解】试题分析:(1)用投中的次数除以投篮的次数即可得出答案;
(2)计算出所有投篮的次数,再计算出总的命中数,继而可估计出这名球员投篮一次,投中的概率.
试题解析:(1)根据题意得:
78÷150=0.52;
104÷209≈0.50;
152÷300≈0.51;
175÷350≈0.58;
填表如下:
投篮次数(n) 50 100 150 209 250 300 350
投中次数(m) 28 60 78 104 123 152 175
投中频率(n/m) 0.56 0.60 0.52 0.50 0.49 0.51 0.58
故答案为0.52,0.50,0.51,0.58;
(2)由题意得:
投篮的总次数是50+100+150+209+250+300+350=1409(次),
投中的总次数是28+60+78+104+123+152+175=720(次),
则这名球员投篮的次数为1409次,投中的次数为720,
故这名球员投篮一次,投中的概率约为:≈0.5.
故答案为0.5
19.(1)0.949,0.950;(2)0.95;(3)400000
【分析】(1)根据表中数据计算即可;
(2)由表中数据可判断频率在0.95左右摆动,从而利于频率估计概率可判断任意抽取一只口罩是合格品的概率为0.95;
(3)用样本数据估计总体即可.
【详解】解:(1)1898÷2000=0.949,2850÷3000=0.950;
故答案为:0.949,0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
(3).
答:该厂估计要生产400000个N95口罩.
【点睛】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.
20.(1)详见解析;(2)详见解析;(3)360.
【分析】(1)根据题和统计表给出的数据即可填写统计表;
(2)根据调整后统计表的数据即可补全条形统计图;
(3)根据抽取的学生中体能测试的优秀率为24%;从而求出该校体能测试为“优秀”的人数.
【详解】解:(1)解:填写的统计表如图1所示:
(2)解:补全的条形统计图如图2所示:
(3)解:抽取的学生中体能测试的优秀率为:12÷50=24%;
∴该校体能测试为“优秀”的人数为1500×24%=360(人)
21.(1)是抽样调查;(2)调查的总体是该校七年级共10个班学生一周中收看电视节目所用的时间,个体是每个同学一周中收看电视节目所用的时间,样本容量是60;(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面
【分析】(1)根据调查的人数与调查的总体进行比较即可得出答案;
(2)总体是指调查对象的全体,个体是总体中的每一个调查的对象,样本容量则是指样本中个体的数量,据此进一步得出答案即可;
(3)根据题意,结合调查的情况进一步分析判断即可.
【详解】(1)小亮的调查是抽样调查;
(2)调查的总体是该校七年级共10个班学生一周中收看电视节目所用的时间;
个体是每个同学一周中收看电视节目所用的时间;
样本容量是60;
(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面.
【点睛】本题主要考查了抽样调查的运用,熟练掌握相关概念是解题关键.
22.(1)1000
(2)20850
(3)63户
【分析】(1)首先计算样本中需要对水龙头、马桶进行改造的家庭所占的百分比,然后根据样本进一步估计总体;
(2)首先计算100户共节约用水量,再进一步计算该社区共节约用水量;
(3)根据题意设未知数,列方程即可求解:改造水龙头数改造马桶数既要改造水龙头又要改造马桶数.
【详解】(1)解:由题意得:估计该社区1200户家庭中需要对水龙头、马桶进行改造的家庭户数为
(户,
故答案为:1000;
(2)解:抽样的120户家庭一年共可节约用水:
(吨.
所以,该社区一年共可节约用水的吨数为(吨.
(3)解:设既要改造水龙头又要改造马桶的家庭共有户,则只改造水龙头不改造马桶的家庭共有户,只改造马桶不改造水龙头的家庭共有户,根据题意列方程,得
,解得,.
所以,既要改造水龙头又要改造马桶的家庭共有63户.
也可以从另一角度考虑,从表中数据可以看出,在这120户中,改造水龙头和改造马桶的户数之和为(户.
由于只有100户需要对水龙头、马桶进行改造,所以多出的就是既要改造水龙头又要改造马桶的家庭.因此,此类家庭的人数为(户.
答:既要改造水龙头又要改造马桶的家庭大约有63户.
【点睛】本题考查获取信息(读表)及综合运用数学知识分析问题、解决问题的能力,用样本估计总体,平均数,一元一次方程的应用,有理数的加法运算,熟练掌握知识点是解题的关键.
23.(1)样本容量为50;(2)平均数为14(岁);中位数为14(岁),众数为15岁;(3)估计该校年龄在15岁及以上的学生人数为720人.
【分析】(1)由12岁的人数除以所占百分比可得样本容量;
(2)先求出14、16岁的人数,再根据平均数、众数和中位数的定义求解可得;
(3)用总人数乘以样本中15、16岁的人数所占比例可得.
【详解】解:(1)样本容量为6÷12%=50;
(2)14岁的人数为50×28%=14、16岁的人数为50﹣(6+10+14+18)=2,
则这组数据的平均数为=14(岁),
中位数为=14(岁),众数为15岁;
(3)估计该校年龄在15岁及以上的学生人数为1800×=720人.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)0.5万人次.
(2)3×30%=0.9万人次.
(3)某教育网站一周内星期日的日访问总量最大.
【分析】(1)由这7天的日访问总量一共约为10万人次,结合条形统计图可得除星期三以外的其它天的日访问总量分别为:0.5万人次,1万人次,1万人次,1.5万人次,2.5万人次,3万人次,继而求得星期三的日访问总量.
(2)由星期日的日访问总量为3万人次,结合扇形统计图可得星期日学生日访问总量占日访问总量的百分比为30%,继而求得星期日学生日访问总量.
(3)结合图可得某教育网站一周内星期日的日访问总量最大(答案不唯一).
【详解】解:(1)∵这7天的日访问总量一共约为10万人次,除星期三以外的其它天的日访问总量分别为:0.5万人次,1万人次,1万人次,1.5万人次,2.5万人次,3万人次,
∴星期三的日访问总量为:10﹣0.5﹣1﹣1﹣1.5﹣2.5﹣3=0.5(万人次).
(2)∵星期日的日访问总量为3万人次,星期日学生日访问总量占日访问总量的百分比为30%,
∴星期日学生日访问总量为:3×30%=0.9(万人次).
(3)某教育网站一周内星期日的日访问总量最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
