华师大版数学七年级上册第五章第1节对顶角同步检测
文档属性
| 名称 | 华师大版数学七年级上册第五章第1节对顶角同步检测 |
|
|
| 格式 | doc | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-21 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学七年级上册第5章第1节5.1.1对顶角同步检测
一、选择题
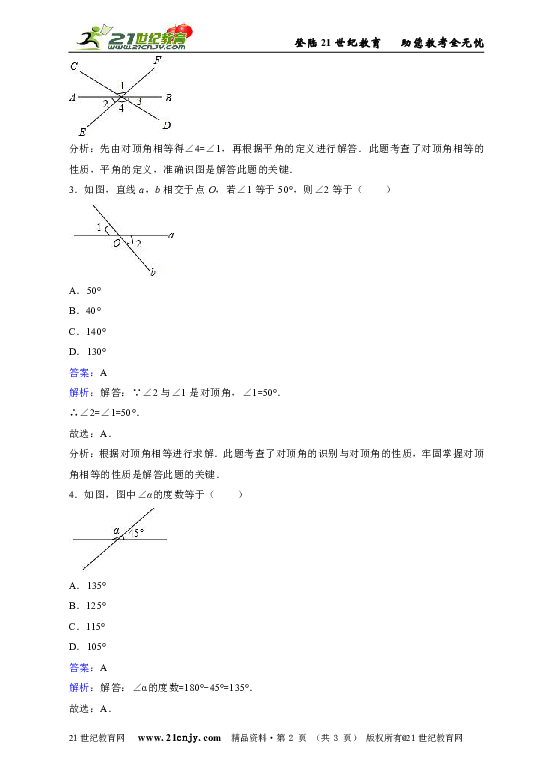
1.如图,∠1和∠2是对顶角的图形个数有( )
A.1个
B.2个
C.3个
D.4个
答案:A
解析:解答:只有丙图中的两个角是对顶角.
故选:A.
分析:一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.由此进行作答.解答此类题的关键是掌握对顶角的概念.
2.如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3的度数为( )
A.90°
B.120°
C.180°
D.不能确定
答案:C
解析:解答:如图,∠4=∠1,
∵∠2+∠3+∠4=180°,
∴∠1+∠2+∠3=180°.
故选:C.
分析:先由对顶角相等得∠4=∠1,再根据平角的定义进行解答.此题考查了对顶角相等的性质,平角的定义,准确识图是解答此题的关键.
3.如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50°
B.40°
C.140°
D.130°
答案:A
解析:解答:∵∠2与∠1是对顶角,∠1=50°.
∴∠2=∠1=50°.
故选:A.
分析:根据对顶角相等进行求解.此题考查了对顶角的识别与对顶角的性质,牢固掌握对顶角相等的性质是解答此题的关键.
4.如图,图中∠α的度数等于( )
A.135°
B.125°
C.115°
D.105°
答案:A
解析:解答:∠α的度数=180°-45°=135°.
故选:A.
分析:根据邻补角互补进行解答.此题考查邻补角定义,关键是根据邻补角互补计算.
5.如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150°
B.130°
C.100°
D.90°
答案:B
解析:解答:∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC,
又已知∠AOD+∠BOC=100°,
∴∠AOD=50°.
∵∠AOD与∠AOC互为邻补角,
∴∠AOC=180°-∠AOD=180°-50°=130°.
故选:B.
分析:两直线相交,对顶角相等,则∠AOD=∠BOC,已知∠AOD+∠BOC=100°,求得∠AOD;又∠AOD与∠AOC互为邻补角,即∠AOD+∠AOC=180°,将∠AOD的度数代入,求得∠AOC.此题考查对顶角的性质以及邻补角的定义.
题型:单选题
6.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
答案:D
解析:解答:根据邻补角的定义,邻补角既有大小关系,又有位置关系.
A.和为180°的两个角只有大小关系,不是邻补角,所以错误;
B.两个角只有公共顶点和大小关系,没有两边关系,所以错误;
C.顶点、另一边的关系不明确,不能确定为邻补角,所以错误;
D.符合邻补角的定义,所以正确.
故选:D.
分析:此题考查邻补角的定义,两条直线相交后所得的有一个公共顶点,有一条边是公共边,另一条边互为反向延长线的两个角叫做邻补角.判断邻补角的关键是互补且相邻.
7.若三条直线交于一点,则共有对顶角(平角除外)( )
A.6对
B.5对
C.4对
D.3对
答案:A
解析:解答:如图:
单个角是对顶角时有3对对顶角,两个角组成一个角时,有3对对顶角,所以,共有:3+3=6对.
故选:A.
分析:画出图形,分单个的角是对顶角,两个角的复合角是对顶角两种情况找出对顶角的对数,然后计算求解.此题主要考查了对顶角的概念,一定要考虑复合角的情况,作出图形更形象直观.
8.下列说法中正确的有( )个.
①对顶角相等;
②相等的角是对顶角;
③若两个角不相等,则这两个角一定不是对顶角;
④若两个角不是对顶角,则这两个角不相等.
A.1
B.2
C.3
D.4
答案:B
解析:解答:②对顶角要符合两直线相交构成的没有公共边的两个相对的角是对顶角,但相等的角不一定是对顶角;④例如30°与30°的角不一定是对顶角,但这两个角一定相等,故②④错误;正确的有①③两个.
故选:B.
分析:根据对顶角的定义和性质判断.此题考查对顶角的性质以及定义.
9.如图,直线AB、CD相交于点O,所形成的∠1、∠2、∠3和∠4中,一定相等的角有( )
A.0对
B.1对
C.2对
D.4对
答案:C
解析:解答:由图可知:∠1和∠2是对顶角,∠3和∠4是对顶角,
根据对顶角相等,
∴∠1=∠2,∠3=∠4,
∴相等的角有2对.
故选:C.
分析:根据对顶角相等,进行解答.此题考查了对顶角的性质,解决此题的关键是熟记对顶角相等.
10.下列图形中,有对顶角的图形是( )
A.
B.
C.
D.
答案:C
解析:解答:根据对顶角的定义可知:有对顶角的图形是C选项.
故选:C.
分析:两条直线相交,有公共顶点而没有公共边的两个角是对顶角,由此进行判断.
11.以下说法正确的是( )
A.有公共顶点,并且相等的两个角是对顶角
B.两条直线相交,任意两个角都是对顶角
C.两角的两边互为反向延长线的两个角是对顶角
D.两角的两边分别在同一直线上,这两个角互为对顶角
答案:C
解析:解答:A.有公共顶点,并且相等的两个角是对顶角,不符合对顶角的定义,所以此选项错误;
B.两角的两边互为反向延长线的两个角是对顶角,且有公共顶点的两个角是对顶角,任意两个角都是对顶角的说法错误;
C.两角的两边互为反向延长线的两个角是对顶角,符合对顶角的定义,所以此选项正确;
D.两角的两边分别在同一直线上,这两个角是对顶角或者邻补角,所以此选项错误.
故选:C.
分析:两条直线相交后所得的只有一个公共顶点并且两个角的两边互为反向延长线,这样的两个角叫做对顶角.两条直线相交,构成的四个角中相邻的角,有公共顶点,两角的两边分别在同一直线上,如果这两条直线互相垂直时,相邻的角还相等,但这样的角不是对顶角.
12.①若a2=b2,则a=b;②对顶角相等;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那∠A与∠B是对顶角.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
答案:C
解析:解答:①若a2=b2,则|a|=|b|,故错误;
②对顶角的性质:对顶角相等,故正确;
③若a,b是有理数,则|a+b|≠|a|+|b|,只有当a,b同号时|a+b|=|a|+|b|,故错误;
④如果∠A=∠B,那∠A与∠B有多种情况,不一定是对顶角,故错误;
所以错误的有3个.
故选:C.
分析:根据绝对值、平方、对顶角的定义和性质进行判断.此题考查了多个知识点的综合应用,注意各个知识点之间的联系.
13.下列命题中,错误的是( )
A.邻补角是互补的角
B.互补的角若相等,则此两角是直角
C.两个锐角的和是锐角
D.一个角的两个邻补角是对顶角
答案:C
解析:解答:A.邻补角有大小关系,即互补,所以正确;
B.互补的角若相等,则都是90°,此两角是直角,所以正确;
C.“两个锐角的和是锐角”是错的,例如:60°+70°=130°中,130°就不是锐角,所以错误;
D.根据两条相交直线的图形,可以看出,一个角的两个邻补角是对顶角,所以正确.
故选:C.
分析:此题考查了对顶角、邻补角及角的相关概念,紧扣定义,进行选择.注意题干中的要求:选“错误”的.
14.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A.m=n
B.m>n
C.m<n
D.m+n=10
答案:A
解析:解答:因为三条直线两两相交与是否交于同一点无关,所以m=n.
故选:A.
分析:三条直线两两相交,每对相交的直线就会形成2对对顶角,这三条直线每两条都相交,相交直线的对数,与是否交于同一点无关,因而m=n.直线相交形成的对顶角的对数,只与有多少对直线相交有关.
15.如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )
A.40°
B.60°
C.80°
D.100°
答案:C
解析:解答:∵∠AOE+∠BOE=180°,∠AOE=140°,
∴∠2=40°,
∵∠1=∠2,
∴∠BOD=2∠2=80°,
∴∠AOC=∠BOD=80°.
故选:C.
分析:根据∠AOE+∠BOE=180°,∠AOE=140°,求得∠2=40°,而∠1=∠2,则∠BOD=80°,再利用对顶角性质求得∠AOC.此题考查了对顶角、邻补角,解题的关键是先求出∠2.
二、填空题
16.如图,直线AB与CD相交所成的四个角中,∠1的邻补角是_ ,∠1的对顶角是 .
答案:∠2和∠4|∠3
解析:解答:由图形可知,∠1的对顶角是∠3,∠1的邻补角是∠2和∠4.
故答案为:∠2和∠4;∠3.
分析:根据对顶角和邻补角的定义进行解答,要注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
17.图中是对顶角量角器,用它测量角的原理是
答案:对顶角相等
解析:解答:由题意得,扇形零件的圆心角与其两边的反向延长线组成的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为:对顶角相等.
分析:由题意知,一个破损的扇形零件的圆心角与其两边的反向延长线组成的角是对顶角,根据对顶角的性质进行解答.此题考查了对顶角的定义、性质,有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,并且对顶角相等.
18.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3= .
答案:180°
解析:解答:∵∠1与∠2是对顶角,
∴∠1=∠2(对顶角相等),
又∵∠1与∠3是邻补角,
∴∠1+∠3=180°,
∴∠2+∠3=180°(等量代换).
故答案为:180°
分析:根据对顶角、邻补角的性质,可得∠1=∠2,∠1+∠3=180°,则∠2+∠3=∠1+∠3=180°.此题主要考查对顶角的性质以及邻补角的定义.
19.已知直线a、b、c两两相交,∠1=2∠3,∠2=40°,则∠4=
答案:20°
解析:解答:∵∠1=∠2=40°,∠1=2∠3,
∴∠3=20°,
∴∠3=∠4=20°,
故答案为:20°.
分析:根据对顶角相等可知∠1=∠2,∠3=∠4,再根据已知条件可知∠3的度数,进而得出∠4的度数.此题主要考查了对顶角相等的性质,学会转化是解答此题的关键.
20.如图,若∠1+∠2=220°,则∠3= .
答案:70°
解析:解答:∵∠1+∠2=220°,∠1=∠2(对顶角相等),
∴∠1=×220°=110°,
∴∠3=180°-∠1=180°-110°=70°.
故答案为:70°.
分析:先根据对顶角相等及已知条件求出∠1的度数,再根据平角等于180°列式进行求解.此题主要考查了对顶角相等的性质,根据对顶角相等求出∠1的度数是解题的关键.
三、解答题
21.如图,已知直线AB、CD交于点O,且∠1:∠2=2:3,∠AOC=60°,求∠2的度数.
答案:36°
解答:设∠1和∠2的比值为x,则∠1=2x,∠2=3x,
∵∠AOC=60°=∠1+∠2,∠1:∠2=2:3
∴2x+3x=60°,x=12°,
则∠2=3x=3×12°=36°.
解析:分析:可设∠1和∠2的比值为x.根据∠AOC=60°和∠1:∠2=2:3,求出x,则可求出∠2的度数.此题考查对顶角的定义和性质.
22.如图,直线a,b,c相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
答案:36°
解答:∵∠1+∠2+∠3=180°,
又∵∠1=∠2,∠3:∠1=8:1,则∠3=8∠1,
∴∠1+∠1+8∠1=180°,则∠1=18°,
∴∠4=∠1+∠2=36°.
解析:分析:利用∠1=∠2,∠3:∠1=8:1的关系,结合平角的定义,先求得∠1,∠2的度数,运用对顶角相等得到∠4的度数.此题考查对顶角的性质以及平角的定义.
23.如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外.如何测量(运用本章知识)?
答案:解答:延长AO与BO得到∠AOB的对顶角∠COD,测出∠COD的度数,则∠AOB=∠COD.
解析:分析:根据对顶角相等的性质,延长AO、BO得到∠AOB的对顶角,测量出对顶角的度数,也就是∠AOB的度数.
24.如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
答案:54°|72°
解答:由已知∠1=∠2,∠1+∠2=162°,
解得:∠1=54°,∠2=108°.
∵∠1与∠3是对顶角,
∴∠3=∠1=54°.
∵∠2与∠4是邻补角,
∴∠4=180°-∠2=72°.
解析:分析:由已知∠1=∠2,∠1+∠2=162°,可求∠1、∠2;又∠1与∠3是对顶角,∠4与∠2是邻补角,根据对顶角,邻补角的数量关系进行求解.解决此题的关键是先求出∠1与∠2的度数,再利用对顶角,邻补角的性质求解.
25.观察下列各图,寻找对顶角(不含平角):
图a
图b
图c
(1)如图a,图中共有______对对顶角;
答案:2
解答:如图a,图中共有1×2=2对对顶角;
(2)如图b,图中共有______对对顶角;
答案:6
解答:如图b,图中共有2×3=6对对顶角;
(3)如图c,图中共有______对对顶角;
答案:12
解答:如图c,图中共有3×4=12对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成______对对顶角;
答案:n(n-1)
解答:研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n-1)对对顶角;
(5)若有2008条直线相交于一点,则可形成______对对顶角.
答案:4 030 056
解答: 若有2008条直线相交于一点,则可形成(2008-1)×2008=4 030 056对对顶角.
解析:分析:由图示可得,(1)两条直线相交于一点,形成2对对顶角;(2)三条直线相交于一点,形成6对对顶角,(3)4条直线相交于一点,形成12对对顶角;(4)依次可找出规律,若有n条直线相交于一点,则可形成n(n-1)对对顶角;(5)将n=2008代入n(n-1),可得2008条直线相交于一点可形成的对顶角的对数.此题考查多条直线相交于一点,所形成的对顶角的个数的计算规律.即若有n条直线相交于一点,则可形成n(n-1)对对顶角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 3 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
华师大版数学七年级上册第5章第1节5.1.1对顶角同步检测
一、选择题
1.如图,∠1和∠2是对顶角的图形个数有( )
A.1个
B.2个
C.3个
D.4个
答案:A
解析:解答:只有丙图中的两个角是对顶角.
故选:A.
分析:一个角的两边分别是另一个角两边的反向延长线,那么这两个角是对顶角.由此进行作答.解答此类题的关键是掌握对顶角的概念.
2.如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3的度数为( )
A.90°
B.120°
C.180°
D.不能确定
答案:C
解析:解答:如图,∠4=∠1,
∵∠2+∠3+∠4=180°,
∴∠1+∠2+∠3=180°.
故选:C.
分析:先由对顶角相等得∠4=∠1,再根据平角的定义进行解答.此题考查了对顶角相等的性质,平角的定义,准确识图是解答此题的关键.
3.如图,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50°
B.40°
C.140°
D.130°
答案:A
解析:解答:∵∠2与∠1是对顶角,∠1=50°.
∴∠2=∠1=50°.
故选:A.
分析:根据对顶角相等进行求解.此题考查了对顶角的识别与对顶角的性质,牢固掌握对顶角相等的性质是解答此题的关键.
4.如图,图中∠α的度数等于( )
A.135°
B.125°
C.115°
D.105°
答案:A
解析:解答:∠α的度数=180°-45°=135°.
故选:A.
分析:根据邻补角互补进行解答.此题考查邻补角定义,关键是根据邻补角互补计算.
5.如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
A.150°
B.130°
C.100°
D.90°
答案:B
解析:解答:∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC,
又已知∠AOD+∠BOC=100°,
∴∠AOD=50°.
∵∠AOD与∠AOC互为邻补角,
∴∠AOC=180°-∠AOD=180°-50°=130°.
故选:B.
分析:两直线相交,对顶角相等,则∠AOD=∠BOC,已知∠AOD+∠BOC=100°,求得∠AOD;又∠AOD与∠AOC互为邻补角,即∠AOD+∠AOC=180°,将∠AOD的度数代入,求得∠AOC.此题考查对顶角的性质以及邻补角的定义.
题型:单选题
6.邻补角是指( )
A.和为180°的两个角
B.有公共顶点且互补的两个角
C.有一条公共边且相等的两个角
D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
答案:D
解析:解答:根据邻补角的定义,邻补角既有大小关系,又有位置关系.
A.和为180°的两个角只有大小关系,不是邻补角,所以错误;
B.两个角只有公共顶点和大小关系,没有两边关系,所以错误;
C.顶点、另一边的关系不明确,不能确定为邻补角,所以错误;
D.符合邻补角的定义,所以正确.
故选:D.
分析:此题考查邻补角的定义,两条直线相交后所得的有一个公共顶点,有一条边是公共边,另一条边互为反向延长线的两个角叫做邻补角.判断邻补角的关键是互补且相邻.
7.若三条直线交于一点,则共有对顶角(平角除外)( )
A.6对
B.5对
C.4对
D.3对
答案:A
解析:解答:如图:
单个角是对顶角时有3对对顶角,两个角组成一个角时,有3对对顶角,所以,共有:3+3=6对.
故选:A.
分析:画出图形,分单个的角是对顶角,两个角的复合角是对顶角两种情况找出对顶角的对数,然后计算求解.此题主要考查了对顶角的概念,一定要考虑复合角的情况,作出图形更形象直观.
8.下列说法中正确的有( )个.
①对顶角相等;
②相等的角是对顶角;
③若两个角不相等,则这两个角一定不是对顶角;
④若两个角不是对顶角,则这两个角不相等.
A.1
B.2
C.3
D.4
答案:B
解析:解答:②对顶角要符合两直线相交构成的没有公共边的两个相对的角是对顶角,但相等的角不一定是对顶角;④例如30°与30°的角不一定是对顶角,但这两个角一定相等,故②④错误;正确的有①③两个.
故选:B.
分析:根据对顶角的定义和性质判断.此题考查对顶角的性质以及定义.
9.如图,直线AB、CD相交于点O,所形成的∠1、∠2、∠3和∠4中,一定相等的角有( )
A.0对
B.1对
C.2对
D.4对
答案:C
解析:解答:由图可知:∠1和∠2是对顶角,∠3和∠4是对顶角,
根据对顶角相等,
∴∠1=∠2,∠3=∠4,
∴相等的角有2对.
故选:C.
分析:根据对顶角相等,进行解答.此题考查了对顶角的性质,解决此题的关键是熟记对顶角相等.
10.下列图形中,有对顶角的图形是( )
A.
B.
C.
D.
答案:C
解析:解答:根据对顶角的定义可知:有对顶角的图形是C选项.
故选:C.
分析:两条直线相交,有公共顶点而没有公共边的两个角是对顶角,由此进行判断.
11.以下说法正确的是( )
A.有公共顶点,并且相等的两个角是对顶角
B.两条直线相交,任意两个角都是对顶角
C.两角的两边互为反向延长线的两个角是对顶角
D.两角的两边分别在同一直线上,这两个角互为对顶角
答案:C
解析:解答:A.有公共顶点,并且相等的两个角是对顶角,不符合对顶角的定义,所以此选项错误;
B.两角的两边互为反向延长线的两个角是对顶角,且有公共顶点的两个角是对顶角,任意两个角都是对顶角的说法错误;
C.两角的两边互为反向延长线的两个角是对顶角,符合对顶角的定义,所以此选项正确;
D.两角的两边分别在同一直线上,这两个角是对顶角或者邻补角,所以此选项错误.
故选:C.
分析:两条直线相交后所得的只有一个公共顶点并且两个角的两边互为反向延长线,这样的两个角叫做对顶角.两条直线相交,构成的四个角中相邻的角,有公共顶点,两角的两边分别在同一直线上,如果这两条直线互相垂直时,相邻的角还相等,但这样的角不是对顶角.
12.①若a2=b2,则a=b;②对顶角相等;③若a,b是有理数,则|a+b|=|a|+|b|;④如果∠A=∠B,那∠A与∠B是对顶角.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
答案:C
解析:解答:①若a2=b2,则|a|=|b|,故错误;
②对顶角的性质:对顶角相等,故正确;
③若a,b是有理数,则|a+b|≠|a|+|b|,只有当a,b同号时|a+b|=|a|+|b|,故错误;
④如果∠A=∠B,那∠A与∠B有多种情况,不一定是对顶角,故错误;
所以错误的有3个.
故选:C.
分析:根据绝对值、平方、对顶角的定义和性质进行判断.此题考查了多个知识点的综合应用,注意各个知识点之间的联系.
13.下列命题中,错误的是( )
A.邻补角是互补的角
B.互补的角若相等,则此两角是直角
C.两个锐角的和是锐角
D.一个角的两个邻补角是对顶角
答案:C
解析:解答:A.邻补角有大小关系,即互补,所以正确;
B.互补的角若相等,则都是90°,此两角是直角,所以正确;
C.“两个锐角的和是锐角”是错的,例如:60°+70°=130°中,130°就不是锐角,所以错误;
D.根据两条相交直线的图形,可以看出,一个角的两个邻补角是对顶角,所以正确.
故选:C.
分析:此题考查了对顶角、邻补角及角的相关概念,紧扣定义,进行选择.注意题干中的要求:选“错误”的.
14.三条直线两两相交于同一点时,对顶角有m对;交于不同三点时,对顶角有n对,则m与n的关系是( )
A.m=n
B.m>n
C.m<n
D.m+n=10
答案:A
解析:解答:因为三条直线两两相交与是否交于同一点无关,所以m=n.
故选:A.
分析:三条直线两两相交,每对相交的直线就会形成2对对顶角,这三条直线每两条都相交,相交直线的对数,与是否交于同一点无关,因而m=n.直线相交形成的对顶角的对数,只与有多少对直线相交有关.
15.如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )
A.40°
B.60°
C.80°
D.100°
答案:C
解析:解答:∵∠AOE+∠BOE=180°,∠AOE=140°,
∴∠2=40°,
∵∠1=∠2,
∴∠BOD=2∠2=80°,
∴∠AOC=∠BOD=80°.
故选:C.
分析:根据∠AOE+∠BOE=180°,∠AOE=140°,求得∠2=40°,而∠1=∠2,则∠BOD=80°,再利用对顶角性质求得∠AOC.此题考查了对顶角、邻补角,解题的关键是先求出∠2.
二、填空题
16.如图,直线AB与CD相交所成的四个角中,∠1的邻补角是_ ,∠1的对顶角是 .
答案:∠2和∠4|∠3
解析:解答:由图形可知,∠1的对顶角是∠3,∠1的邻补角是∠2和∠4.
故答案为:∠2和∠4;∠3.
分析:根据对顶角和邻补角的定义进行解答,要注意两直线相交,一个角的对顶角只有一个,但邻补角有两个.
17.图中是对顶角量角器,用它测量角的原理是
答案:对顶角相等
解析:解答:由题意得,扇形零件的圆心角与其两边的反向延长线组成的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为:对顶角相等.
分析:由题意知,一个破损的扇形零件的圆心角与其两边的反向延长线组成的角是对顶角,根据对顶角的性质进行解答.此题考查了对顶角的定义、性质,有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角,并且对顶角相等.
18.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3= .
答案:180°
解析:解答:∵∠1与∠2是对顶角,
∴∠1=∠2(对顶角相等),
又∵∠1与∠3是邻补角,
∴∠1+∠3=180°,
∴∠2+∠3=180°(等量代换).
故答案为:180°
分析:根据对顶角、邻补角的性质,可得∠1=∠2,∠1+∠3=180°,则∠2+∠3=∠1+∠3=180°.此题主要考查对顶角的性质以及邻补角的定义.
19.已知直线a、b、c两两相交,∠1=2∠3,∠2=40°,则∠4=
答案:20°
解析:解答:∵∠1=∠2=40°,∠1=2∠3,
∴∠3=20°,
∴∠3=∠4=20°,
故答案为:20°.
分析:根据对顶角相等可知∠1=∠2,∠3=∠4,再根据已知条件可知∠3的度数,进而得出∠4的度数.此题主要考查了对顶角相等的性质,学会转化是解答此题的关键.
20.如图,若∠1+∠2=220°,则∠3= .
答案:70°
解析:解答:∵∠1+∠2=220°,∠1=∠2(对顶角相等),
∴∠1=×220°=110°,
∴∠3=180°-∠1=180°-110°=70°.
故答案为:70°.
分析:先根据对顶角相等及已知条件求出∠1的度数,再根据平角等于180°列式进行求解.此题主要考查了对顶角相等的性质,根据对顶角相等求出∠1的度数是解题的关键.
三、解答题
21.如图,已知直线AB、CD交于点O,且∠1:∠2=2:3,∠AOC=60°,求∠2的度数.
答案:36°
解答:设∠1和∠2的比值为x,则∠1=2x,∠2=3x,
∵∠AOC=60°=∠1+∠2,∠1:∠2=2:3
∴2x+3x=60°,x=12°,
则∠2=3x=3×12°=36°.
解析:分析:可设∠1和∠2的比值为x.根据∠AOC=60°和∠1:∠2=2:3,求出x,则可求出∠2的度数.此题考查对顶角的定义和性质.
22.如图,直线a,b,c相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
答案:36°
解答:∵∠1+∠2+∠3=180°,
又∵∠1=∠2,∠3:∠1=8:1,则∠3=8∠1,
∴∠1+∠1+8∠1=180°,则∠1=18°,
∴∠4=∠1+∠2=36°.
解析:分析:利用∠1=∠2,∠3:∠1=8:1的关系,结合平角的定义,先求得∠1,∠2的度数,运用对顶角相等得到∠4的度数.此题考查对顶角的性质以及平角的定义.
23.如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外.如何测量(运用本章知识)?
答案:解答:延长AO与BO得到∠AOB的对顶角∠COD,测出∠COD的度数,则∠AOB=∠COD.
解析:分析:根据对顶角相等的性质,延长AO、BO得到∠AOB的对顶角,测量出对顶角的度数,也就是∠AOB的度数.
24.如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
答案:54°|72°
解答:由已知∠1=∠2,∠1+∠2=162°,
解得:∠1=54°,∠2=108°.
∵∠1与∠3是对顶角,
∴∠3=∠1=54°.
∵∠2与∠4是邻补角,
∴∠4=180°-∠2=72°.
解析:分析:由已知∠1=∠2,∠1+∠2=162°,可求∠1、∠2;又∠1与∠3是对顶角,∠4与∠2是邻补角,根据对顶角,邻补角的数量关系进行求解.解决此题的关键是先求出∠1与∠2的度数,再利用对顶角,邻补角的性质求解.
25.观察下列各图,寻找对顶角(不含平角):
图a
图b
图c
(1)如图a,图中共有______对对顶角;
答案:2
解答:如图a,图中共有1×2=2对对顶角;
(2)如图b,图中共有______对对顶角;
答案:6
解答:如图b,图中共有2×3=6对对顶角;
(3)如图c,图中共有______对对顶角;
答案:12
解答:如图c,图中共有3×4=12对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成______对对顶角;
答案:n(n-1)
解答:研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成n(n-1)对对顶角;
(5)若有2008条直线相交于一点,则可形成______对对顶角.
答案:4 030 056
解答: 若有2008条直线相交于一点,则可形成(2008-1)×2008=4 030 056对对顶角.
解析:分析:由图示可得,(1)两条直线相交于一点,形成2对对顶角;(2)三条直线相交于一点,形成6对对顶角,(3)4条直线相交于一点,形成12对对顶角;(4)依次可找出规律,若有n条直线相交于一点,则可形成n(n-1)对对顶角;(5)将n=2008代入n(n-1),可得2008条直线相交于一点可形成的对顶角的对数.此题考查多条直线相交于一点,所形成的对顶角的个数的计算规律.即若有n条直线相交于一点,则可形成n(n-1)对对顶角.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 3 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
