6.6图形的位似同步强化练习（含解析）

中小学教育资源及组卷应用平台
6.6图形的位似
学校:___________姓名：___________班级：___________考号：___________
一、单选题
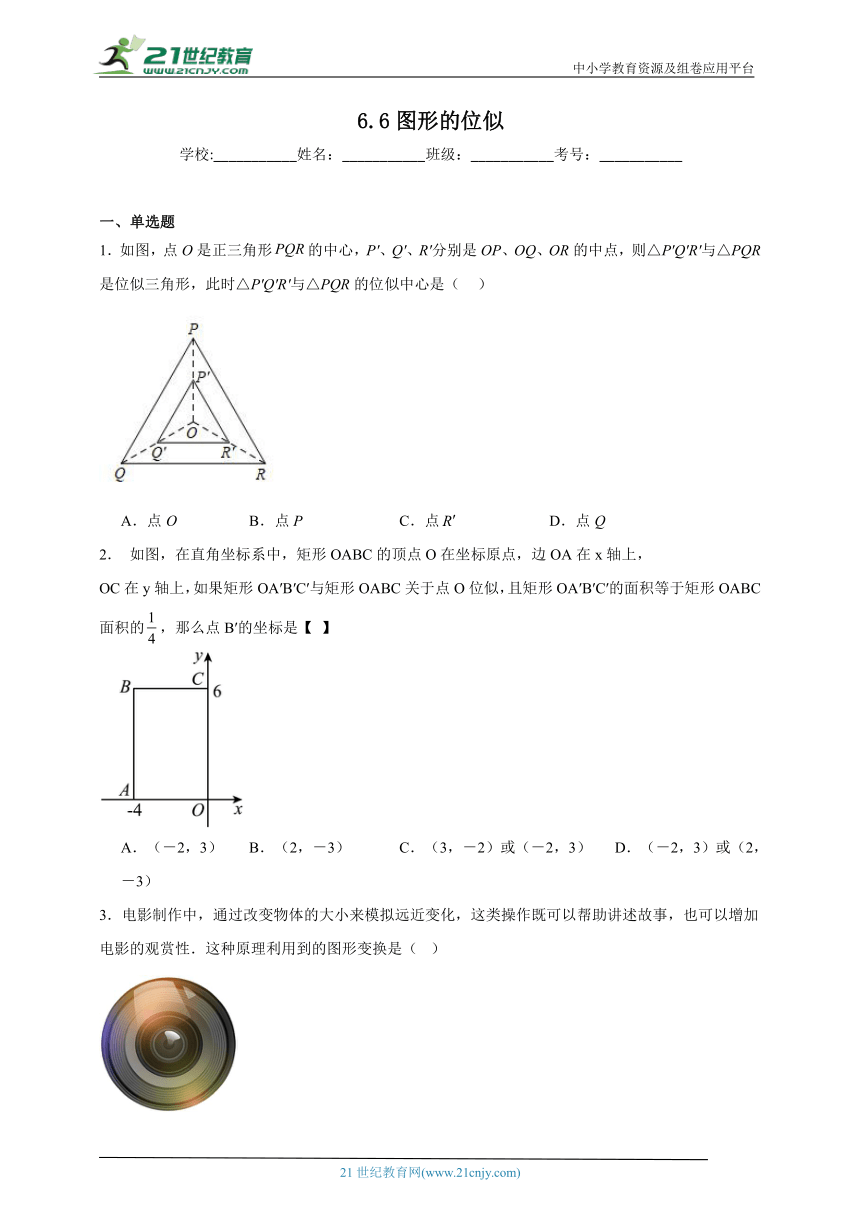
1．如图，点O是正三角形的中心，P′、Q′、R′分别是OP、OQ、OR的中点，则△P′Q′R′与△PQR是位似三角形，此时△P′Q′R′与△PQR的位似中心是（ ）
A．点O B．点P C．点 D．点Q
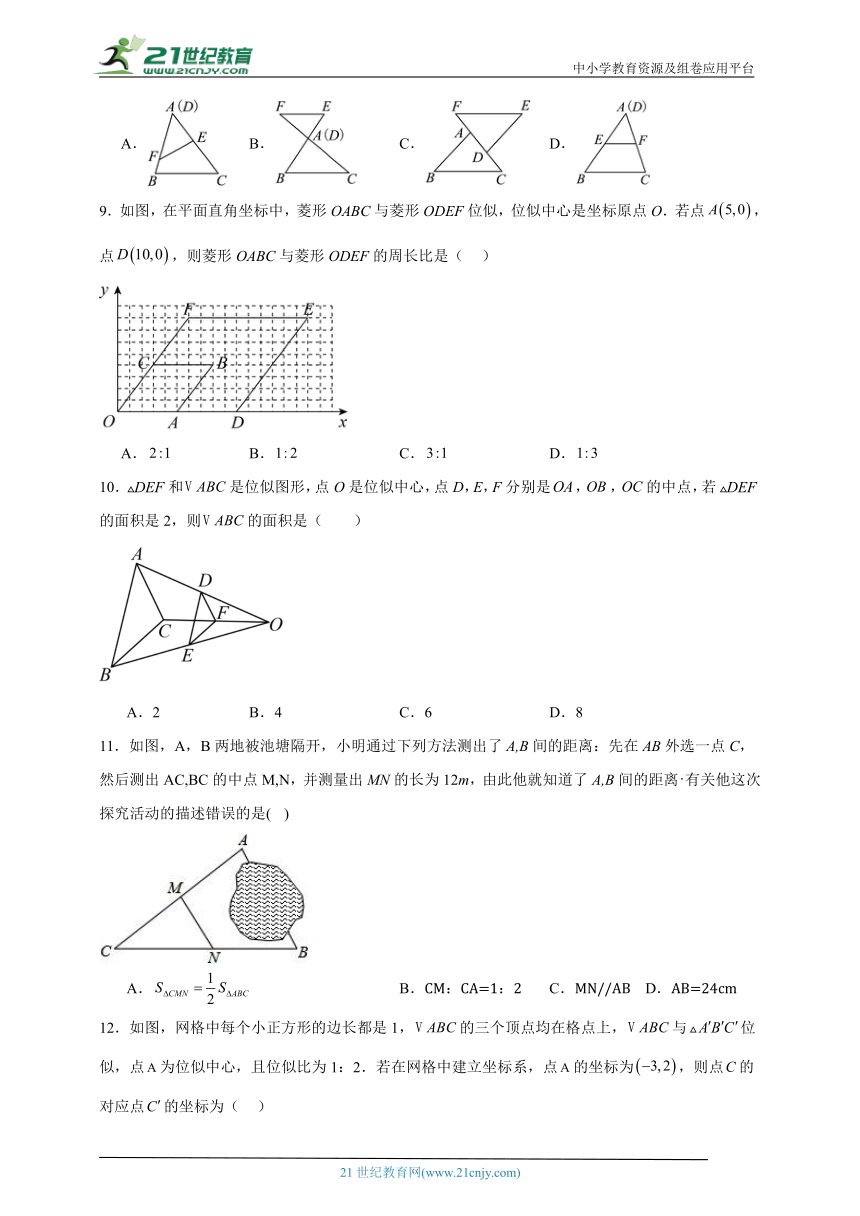
2． 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，
OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是【 】
A．（－2，3） B．（2，－3） C．（3，－2）或（－2，3） D．（－2，3）或（2，－3）
3．电影制作中，通过改变物体的大小来模拟远近变化，这类操作既可以帮助讲述故事，也可以增加电影的观赏性．这种原理利用到的图形变换是（ ）
A．位似变换 B．平移变换 C．对称变换 D．旋转变换
4．如图，以点O为位似中心，将五边形ABCDE放大后得到五边形，已知cm， cm，则五边形ABCDE与五边形的周长比是（ ）
A． B． C． D．
5．如图，与位似，位似中心是点O，若，则与的面积比是（ ）

A． B． C． D．
6．如图，在直角坐标系中，的顶点分别为，，以点为位似中心，在第三象限内作位似图形，与的位似比为，则点的坐标为（ ）
A． B． C． D．
7．下列说法中正确的是（ ）
A．位似图形可以通过平移而相互得到
B．位似图形的对应边平行且相等
C．位似图形的位似中心不只有一个
D．位似中心到对应点的距离之比都相等
8．下列图形中，则这两个三角形不是位似图形的是（ ）
A． B． C． D．
9．如图，在平面直角坐标中，菱形OABC与菱形ODEF位似，位似中心是坐标原点O．若点，点，则菱形OABC与菱形ODEF的周长比是（ ）
A． B． C． D．
10．和是位似图形，点O是位似中心，点D，E，F分别是，，的中点，若的面积是2，则的面积是（　　）
A．2 B．4 C．6 D．8
11．如图，A，B两地被池塘隔开，小明通过下列方法测出了A,B间的距离：先在AB外选一点C，然后测出AC,BC的中点M,N，并测量出MN的长为12m，由此他就知道了A,B间的距离有关他这次探究活动的描述错误的是( )
A． B．CM：CA=1：2 C．MN//AB D．AB=24cm
12．如图，网格中每个小正方形的边长都是1，的三个顶点均在格点上，与位似，点为位似中心，且位似比为1：2．若在网格中建立坐标系，点的坐标为，则点的对应点的坐标为（ ）
A． B．或 C． D．或
二、填空题
13．如图，与是位似图形，点O为位似中心，若，则与的面积比为 ．
14．如图，△OAB与△OCD是以点O为位似中心的位似图形，点B在OD上，AE、CB分别是△OAB、△OCD的中线，则AE：CB的值为
15．如图，线段两个端点的坐标分别为，以原点为位似中心，将线段放大得到线段．若点的坐标为，则点的坐标为 ．
16．如图，点是四边形内一点，、、、分别是、、、上的点，且，若四边形的面积为，则四边形的面积为 ．
17．在平面直角坐标系中，三个顶点的坐标分别为．以原点为位似中心，把这个三角形缩小为原来的，得到，则点的对应点的坐标是 ．
三、解答题
18．已知：如图，△ABC三个顶点的坐标分别为A（0，-3）、B（3，-2）、C（2，-4），正方形网格中，每个小正方形的边长是1个单位长度．
(1)画出△ABC向上平移6个单位得到的；
(2)以点C为位似中心，在网格中画出，使与△ABC位似，且与△ABC的位似比为2：1，并直接写出点的坐标．
19．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．
(1)以原点O为位似中心，位似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点的坐标；
(2)如果点D(a，b)在线段AB上，请直接写出经过(1)的变化后点D的对应点D1的坐标．
20．如图，在平面直角坐标系中，的顶点坐标分别是，，，以原点为位似中心，在坐标系内画，使它与位似，且位似比为．
(1)画出；
(2)请直接写出△DEF的顶点坐标．
21．已知边长为1的正方形，以它的两条对角线的交点为位似中心，画一个边长为2并与它位似的正方形．
22．将如图所示的图形缩小，使得缩小前后对应线段的比为．
23．如图，图中的小方格都是边长为1的正方形，在方格纸中．
(1)请在方格纸上建立平面直角坐标系，使，则B点坐标为____________；
(2)以原点O为位似中心，相似比为2，在第一象限内将放大，画出放大后的图形；
(3)的面积为____________．
24．在正方形网格中，每个小正方形的边长为1，△ABC在平面直角坐标系中的位置如图所示．
(1)画出△ABC沿x轴翻折后的△A1B1C1；
(2)以点M为位似中心，在网格中作出△A1B1C1的位似图形△A2B2C2，使其位似比为2：1；
(3)点A2的坐标______；△ABC与△A2B2C2的周长比是______．
《6.6图形的位似》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B C D D A B D
题号 11 12
答案 A D
1．A
【分析】先根据三角形中位线定理可得P′Q′∥PQ，P′R′∥PR，Q′R′∥QR，，得出△P′Q′R′∽△PQR，再根据位似中心的定义：如果两个图形不仅是相似图形而且每组对应点所在的直线都经过同一点，对应边互相平行（或共线），那么这样的两个图形叫位似图形，这个点叫做位似中心即可得．
【详解】解：∵P′、Q′、R′分别是OP、OQ、OR的中点，
∴P′Q′∥PQ，P′R′∥PR，Q′R′∥QR，，
∴△P′Q′R′∽△PQR，
又∵点P′在PO中点、点Q′在QO中点、点R′在RO中点，
∴点P′与点P，点Q′与点Q，点R′与点R的连线都经过点O，
∴△P′Q′R′与△PQR是位似三角形，其位似中心是点O，
故选：A．
【点睛】本题考查了三角形的中位线定理、相似三角形的判定、位似图形与位似中心，熟记位似图形与位似中心的定义是解题关键．
2．D
【详解】如果两个图形不仅是相似图形，而且每组对应点的连线交于一点，对应边互相平行或在一
条直线上，那么这两个图形叫做位似图形．把一个图形变换成与之位似的图形是位似变换．因此，
∵矩形OA′B′C′与矩形OABC关于点O位似，∴矩形OA′B′C′∽矩形OABC．
∵矩形OA′B′C′的面积等于矩形OABC面积的，∴位似比为：．
∵点B的坐标为（－4，6），∴点B′的坐标是：（－2，3）或（2，－3）．故选D．
3．A
【分析】本题考查图形变换的位似变换，特别是位似变换在实际场景（电影制作）中的应用．
【详解】首先分析题目中提到的电影制作中通过改变物体大小模拟远近变化这一现象；
然后依次回顾平移变换、对称变换、旋转变换和位似变换的定义和特点．
平移变换只是位置改变，大小和形状不变，B项不符合题意；
对称变换是关于某条直线对称，图形的大小也未发生改变，C项不符合题意；
旋转变换是绕定点旋转一定角度，同样不涉及大小的变化，D项不符合题意；
位似变换可以使图形按照一定比例放大或缩小，与电影中物体大小变化模拟远近的原理相符，A正确．BCD不符合题意．
故选A．
4．B
【分析】根据位似的性质解答即可.
【详解】因为五边形ABCDE与五边形是位似图形，cm，cm，
所以五边形ABCDE与五边形'相似，且相似比是1：2，
所以五边形ABCDE与五边形的周长比也是1：2.
故选B.
【点睛】本题考查了位似图形的性质，熟练掌握位似图形高、周长的比都等于相似比是解答本题的关键.
5．C
【分析】根据位似图形的概念得到，，进而得出，根据相似三角形的性质解答即可．
【详解】解：与位似，
，，
，，
，
，
与的面积比为，
故选：C．
【点睛】本题考查的是位似图形的概念、相似三角形的性质，掌握位似图形是相似图形、位似图形的对应边平行是解题的关键．
6．D
【分析】本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为，那么位似图形对应点的坐标的比等于或．
根据以原点为位似中心的对应点的坐标特征，把点的横纵坐标都乘以得到点的坐标．
【详解】解：以点为位似中心，在第三象限内作位似图形，与的位似比为，
点的坐标为，即.
故选：D．
7．D
【详解】试题分析：∵位似是相似的特殊形式，
∴位似图形的对应边平行但不一定相等，
位似图形的位似中心只有一个，
平移图形是全等图形，也没有位似中心．
位似中心到对应点的距离之比都相等
∴正确答案为D．
故选D．
考点：位似变换．
8．A
【分析】根据位似图形的性质，①两个图形必须是相似形；②对应点的连线都经过同一点；③对应边平行，对各选项逐一分析，即可得出答案．
【详解】对应顶点的连线相交于一点的两个相似多边形叫位似图形．
根据位似图形的概念， C、B、D三个图形中的两个图形都是位似图形；
A中的两个图形不符合位似图形的概念，对应边不平行，故不是位似图形．
故选：A．
【点睛】此题考查位似图形，解题关键在于掌握位似与相似既有联系又有区别，相似仅要求两个图形形状完全相同；而位似是在相似的基础上要求对应点的连线相交于一点．
9．B
【分析】根据点，点得到OA=5， OD=10，根据相似形的性质求出得到答案．
【详解】解：点，点，
OA=5， OD=10，
菱形OABC与菱形ODEF位似，位似中心是坐标原点O．
菱形OABC周长菱形ODEF周长=，
故选：B．
【点睛】本题考查的是位似图形的概念、相似三角形的性质，掌握位似图形是相似图形、对应边平行是解题的关键．
10．D
【分析】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．先根据三角形中位线的性质得到，从而得到相似比，再利用位似的性质得到，然后根据相似三角形的面积比是相似比的平方求解即可．
【详解】解：∵点D，E，F分别是，，的中点，
∴，
∴和的相似比是，
∴，即，
解得：．
故选：D．
11．A
【详解】解：∵AC，BC的中点M，N，∴MN∥AB，MN=AB，∴△CMN∽△CAB，∴S△CNM：S△ACB=，∴S△CNM：S△ACB=1：4，∴S△CMN=S△ABC，故A描述错误；
∵M是AC中点，∴CM：CA=1：2，故B描述正确；
∵AC，BC的中点M，N，∴MN∥AB，故C描述正确；
∵MN的长为12m，MN=AB，∴AB=24m，故D描述正确．
故选A．
点睛：本题主要考查了三角形的中位线，以及相似三角形的性质，关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半．
12．D
【分析】根据位似变换的概念和性质、结合图形解答．
【详解】解：如图，
由图可知，点C的坐标为(-2，3)，
以点A为位似中心，在网格中画，使与△ABC位似，且位似比为1：2，
则点的坐标为(-5，0)或(-1，4)，
故选：D．
【点睛】本题考查位似变换的应用，熟练掌握位似变换的概念和性质是解题关键．
13．
【分析】先求出相似比为，再根据位似图形的性质即可得．
【详解】解：，
，
与是位似图形，
与的相似比为，
，
即与的面积比为，
故答案为：．
【点睛】本题考查了位似图形，熟练掌握位似图形的性质是解题关键．
14．1：2
【分析】由△OAB与△OCD是以点O为位似中心的位似图形，得出相似比解答即可．
【详解】∵△OAB与△OCD是以点O为位似中心的位似图形．
又∵AE、CB分别是△OAB、△OCD的中线，∴相似比是，∴AE：CB=1：2．
故答案为1：2．
【点睛】本题考查了位似变换的性质，正确理解位似与相似的关系进行解答．
15．
【分析】本题考查了位似变换，坐标与图形性质，熟练掌握位似变换的概念，相似三角形的性质是解答问题的关键．
根据位似变换的概念得到，求出相似比，计算即可．
【详解】解：根据题意得与是位似图形，
，
，
，
与的位似比为，
点的坐标为，即，
故答案为： ．
16．
【分析】本题主要考查了位似变换．利用位似图形的定义得出四边形与四边形的位似比为：，进而得出面积比，即可得出四边形的面积．
【详解】解：，
，
四边形与四边形的位似比为：，
四边形与四边形的面积比为：，
四边形的面积为，
四边形的面积为：．
故答案为：．
17．或
【分析】根据位似图形的中心和位似比例即可得到点A的对应点C.
【详解】解：以原点为位似中心，把这个三角形缩小为原来的，点的坐标为，
∴点的坐标为或，即或，
故答案为或．
【点睛】本题主要考查位似图形的对应点，关键在于原点的位似图形，要注意方向.
18．(1)见解析
(2)图见解析，坐标为（2，-4）
【分析】（1）直接利用平移的性质得出对应点位置即可得出答案；
（2）直接利用位似图形的性质以C为位似中心，将边长扩大为原来的2倍即可．
【详解】（1）如图所示：即为所求；
（2）如图所示：即为所求，
坐标为：（2，-4）．
【点睛】本题考查了平移的性质，位似的性质，能根据性质的特点进行画图是解此题的关键．
19．(1)图见解析，C1(－6，4)；(2)D1(2a，2b)．
【分析】（1）连接OB并延长，使BB1=OB，连接OA并延长，使AA1=OA，连接OC并延长，使CC1=OC，确定出△A1B1C1，并求出C1点坐标即可；
（2）根据A与A1坐标，B与B1坐标，以及C与C1坐标的关系，确定出变化后点D的对应点D1坐标即可．
【详解】（1）根据题意画出图形，如图所示：
则点C1的坐标为（-6，4）；
（2）变化后D的对应点D1的坐标为：（2a，2b）．
【点睛】运用了作图-位似变换，画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．
20．(1)作图见详解
(2)D的坐标为，E的坐标为，F的坐标为
【分析】
（1）根据位数定义，及位似比即可作图；
（2）的顶点坐标分别是，，，以原点为位似中心，位似比为，由此可求出对应点的坐标．
【详解】（1）解：原点为位似中心，位似比为，
∴如图所示，
和即为所求．
（2）解：的顶点坐标分别是，，，以原点为位似中心，位似比为，
∴，，，， ，．
【点睛】本题主要考查图形的位似，掌握位似图形的定义及位似比的计算是解题的关键．
21．见解析
【分析】取正方形ABCD的对角线AC和BD的交点O为位似中心，再分别将OA、OB、OC、OD延长一倍，得到对应的点、、、，然后顺次连接、、、，则利用位似的判定方法可判断四边形满足条件．
【详解】解：如图，正方形即为所求．
【点睛】本题考查了作图-位似变换：画位似图形的一般步骤，先确定位似中心，再分别连接并延长位似中心和能代表原图的关键点，接着根据位似比，确定能代表所作的位似图形的关键点，然后顺次连接上述各点，得到放大或缩小的图形．
22．见解析
【分析】取正六边形的中心点为位似中心，连接点和图形的各个顶点，然后取连接线段的中点，最后依次连接各个中点即可．
【详解】解：取正六边形的中心点为位似中心，连接点和图形的各个顶点，
取每个连接线段的中点，依次连接各个中点，如下图：
【点睛】此题考查了作图—位似变换，先确定位似中心，再分别连接位似中心与原图的关键点，再根据位似比确定关键点是解题的关键．
23．(1)图见解析，；
(2)见解析；
(3)
【分析】
（1）根据点A、C的坐标可确定平面直角坐标系的位置，进而可得出点B的坐标；
（2）根据位似图形的性质确定A、B、C对应点的位置，再顺次连接即可；
（3）根据网格特点直接利用三角形的面积公式求解即可．
【详解】（1）解：建立平面直角坐标系如图所示，则点B坐标为，
故答案为：；
（2）解：如图所示：即为所求
（3）解：由图可知，，
故答案为：．
【点睛】本题考查建立平面直角坐标系、画位似图形、三角形的面积，熟练掌握位似图形的画法是解答的关键．
24．(1)见解析
(2)见解析
(3)，
【分析】（1）利用网格特点和旋转的性质画出A、B的对应点A1、B1即可；
（2）延长M A1到A2使MA2=2MA1，延长MB1到B2使MB2=2MB1，延长MC1到C2使MC2=2MC1，则可得到△A2B2C2，
（3）根据（2）可写出点A2的坐标；然后根据位似的性质可得△ABC与△A2B2C2的周长比
【详解】（1）如图，△A1B1C1即为所作；
（2）如图，△A2B2C2即为所作；
（3）由（2）得，点的坐标，
由作图得，
∵与周长比为1:2
∴△ABC与△A2B2C2的周长比是1:2
故答案为：，1:2
【点睛】本题考查了作图-位似变换：画位似图形的一般步骤为：先确定位似中心；再分别连接并延长位似中心和能代表原图的关键点；然后根据位似比，确定能代表所作的位似图形的关键点；最后顺次连接上述各点，得到放大或缩小的图形．也考查了轴对称变换．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)