7.5解直角三角形同步强化练习(含解析)
文档属性
| 名称 | 7.5解直角三角形同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.5解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
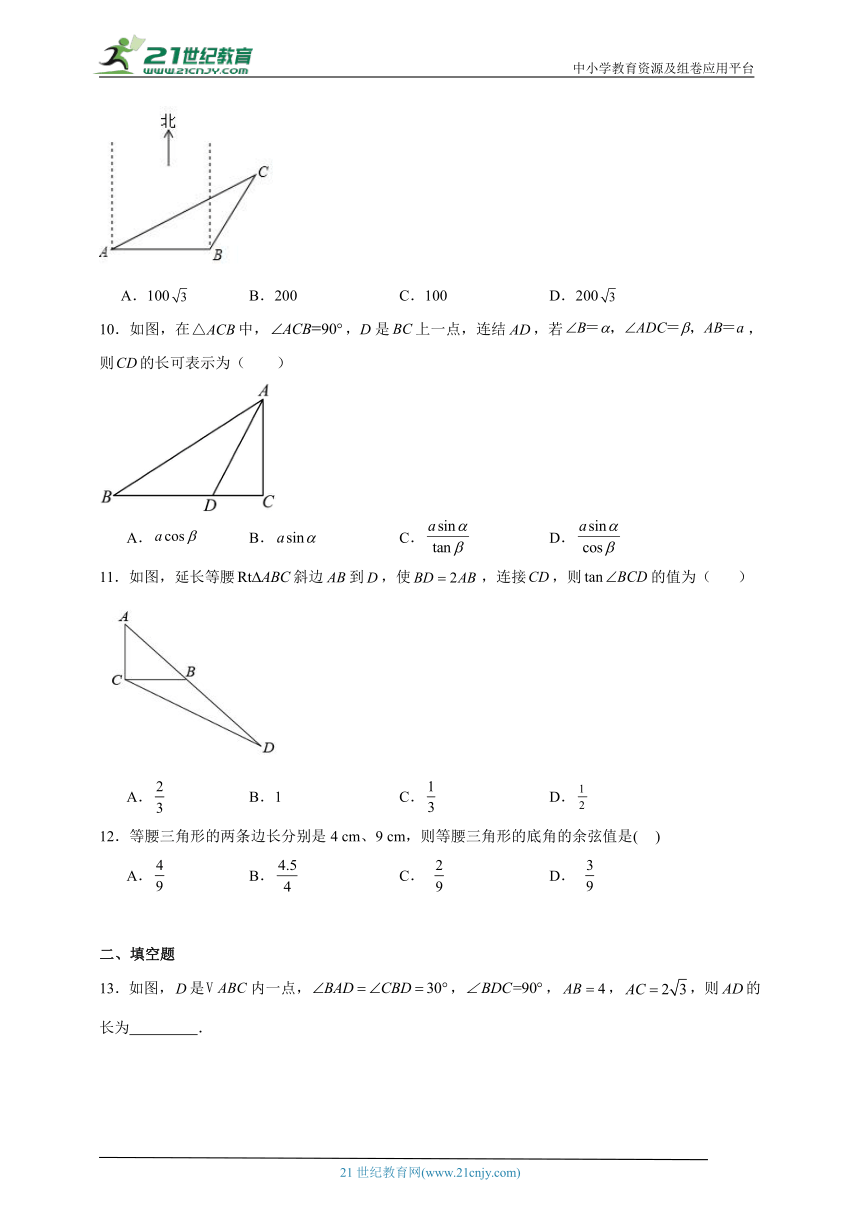
1.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
2.已知在中,,,则的值为( )
A. B. C. D.
3.在△ABC中,∠C=90°,且已知b和∠B,下列求c的表达式正确的是( )
A.c=bcosB B.c=bsinB C.c= D.c=
4.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. B. C. D.
5.如图,是用12个相似的直角三角形组成的图案.若,则的长度为( )
A. B. C. D.
6.如图,线杆DC的高度为,两根拉线与互相垂直,,若、、在同一条直线上,则拉线的长度为( )
A. B. C. D.
7.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
8.如图所示,平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成60°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )
A. B. C. D.
9.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100 B.200 C.100 D.200
10.如图,在中,,D是上一点,连结,若,则的长可表示为( )
A. B. C. D.
11.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
12.等腰三角形的两条边长分别是4 cm、9 cm,则等腰三角形的底角的余弦值是( )
A. B. C. D.
二、填空题
13.如图,是内一点,,,,,则的长为 .
14.如图,已知半的直径为3,弦与弦交于点,,垂足为点,,则弦的长为 .
15.四边形ABCD中,∠C=90°,AB=12,BC=4,CD=3,AD=13,则四边形ABCD的面积为 .
16.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则=
17.在Rt△ABC中,∠C=90°,BC=,AB=,则∠B= .
三、解答题
18.在△ABC中,AB=2,AC=,∠B=30°.求∠BAC的度数.
19.在Rt中,,,,求,的度数.
20.在中,,所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素:
(1);
(2).
21.如图,在中,,,的平分线,求的度数及边,的长.
22.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
23.如图,已知:内接于⊙O,是⊙O的切线,的延长线交于点.
(1)若∠B=2∠D ,求∠D的度数;
(2)在(1)的条件下,若,求⊙O的半径.
24.如图,在中,,,,垂足为G,且,E为的中点,.
(1)求证:是等边三角形.
(2)过点G作于点F,连接、,求的长.
《7.5解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C C C B D B B C
题号 11 12
答案 A C
1.C
【分析】设BP=x(x≥0),过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,利用正弦三角函数求得S△PBC ,S△ADQ,当两三角形的面积和最小时,四边形的面积最大,根据x≥0即可判断;
【详解】解:如图,过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,设BP=x(x≥0),则AQ=3--x=-x,
∵△ABC是等边三角形,∴∠A=∠B=60°,
∴,,,
∴S△PBC=,
S△ADQ,
S△ABC=,
S△PBC+S△ADQ=≥(x=0时,有最小值),
∴四边形PCDQ面积≤-=,
故选: C.
【点睛】,本题考查了正弦三角函数,等边三角形的性质,根据面积关系正确作出辅助线是解题关键.
2.D
【分析】根据正弦三角函数的定义,设,则,,再根据正切三角函数的定义,即可求解.
【详解】
∵在中,,,
∴,
设,则,,
∴,
故选:D.
【点睛】本题主要考查三角函数的定义,根据三角函数的定义,用未知数表示出直角三角形的各边长,是解题的关键.
3.C
【详解】试题解析:在中,,
故选C.
4.C
【分析】根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根据全等三角形的性质可得出OE=OB、EF=BP,设EF=x,则BP=x、DF=4﹣x、BF=PC=3﹣x,进而可得出AF=1+x,在Rt△DAF中,利用勾股定理可求出x的值,再利用余弦的定义即可求出cos∠ADF的值.
【详解】根据折叠,可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP.
设EF=x,则BP=x,DF=DE﹣EF=4﹣x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,
∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,
解得:x=,
∴DF=4﹣x=,
∴cos∠ADF=,
故选C.
【点睛】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合AF=1+x,求出AF的长度是解题的关键.
5.C
【分析】本题考查的是相似三角形的性质,锐角三角函数的应用,规律探究;
先求解,可得,再进一步探究即可;
【详解】解:∵12个相似的直角三角形,
∴,
,
∵,
∴,
,
,
∴,
故选:C
6.B
【分析】根据同角的余角相等得∠CAD=∠BCD,由,即可求出BC的长度.
【详解】解:∵两根拉线与互相垂直,DC垂直AB,
∴∠CAB+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAB=∠BCD,
∵,∴
在Rt△BCD中,;
∴
故选:B.
【点睛】本题主要考查解直角三角形,熟练掌握同角的余角相等和三角函数的定义是解题的关键.
7.D
【详解】试题分析:∵∠C=90°,∠A=40°,∴∠B=50°.
∵BC=3,,∴.
故选D.
考点:1.直角三角形两锐角的关系;2.锐角三角函数定义.
8.B
【详解】解:CD=BD-BC=.
故选B.
9.B
【详解】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B.
10.C
【分析】利用锐角三角函数关系分别表示出的长进而得出答案.
【详解】解:∵,,
∴,
则,
,
故,
则,
故,
故选:C.
【点睛】此题主要考查了锐角三角函数的定义,正确掌握三角函数是解题关键.
11.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
【点睛】本题主要考查了勾股定理,等腰直角三角形的性质,解直角三角形,熟练解直角三角形是解题的关键.
12.C
【分析】等腰三角形两边的长为4cm和9cm,题目没有明确说明哪条是底边,哪条是腰,因此要分两种情况讨论;
对每一种情况,还需利用三角形三边关系验证能否构成三角形,若能构成三角形,再根据等腰三角形的性质以及余弦的定义进一步解答即可得到答案.
【详解】①当腰长为4cm时,则另外两边长分别为4cm和9cm,
4+4=8<9,不满足三角形三边关系,即此三角形不存在;
②当腰长为9cm时,则另外两边长分别为9cm和4cm,满足三角形三边关系,如图,
过A作AD⊥BC,垂足为D.
∵ AB=AC AD⊥BC,
∴ BD=DC (三线合一),
∵ BD=DC ,BC=4,
∴ DC=2,
∵ AD⊥BC DC=2, AC=9,
∴ cos∠BCA= =,即等腰三角形的底角的余弦值是 .
故选C.
【点睛】本题考查等腰三角形和三角函数的知识,解答本题需掌握等腰三角形三线合一的性质以及余弦的定义.
13.
【分析】过点作的垂线,过点作的垂线,两垂线交于点,连接,证明,由相似三角形的性质得出,证明,得出,求出,由勾股定理求出AM,最后由直角三角形的性质可求出的长.
【详解】如图,过点作的垂线,过点作的垂线,两垂线交于点,连接,
,
,
,
,
又,
,
,
,
,即,
,
,
,
,
在中,,
.
【点睛】此题考查了解直角三角形,勾股定理,相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.
14.
【分析】由AC=BD知 ,得 ,根据OD⊥AC知,从而得,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
【详解】∵OD⊥AC,
∴,∠AFO=90°,
又∵AC=BD,
∴,即,
∴,
∴,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=3,
∴AF=AOsin∠AOF=,
则AC=2AF=;
【点睛】本题考查圆心角,弧,弦之间的关系,解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
15.36
【分析】先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可.
【详解】如图,
∵∠C=90°CD=3,BC=4
∴BD===5
在△ABD中,AB2+BD2=25+144=169=AD2,
∴△ABD是直角三角形,
∴S四边形ABCD=AB BD+BC CD,
=×5×12+×3×4,
=36.
故答案为36
【点睛】本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键.
16.
【分析】先根据∠D的正切值设AB=2x,AD=3x,然后根据等腰直角三角形的性质求出CD的长,即可求解.
【详解】解:在Rt△ABD中,
∵
∴设AB=2x,AD=3x,
∵∠ACB=45°,
∴AC=AB=2x,
则CD=AD﹣AC=3x﹣2x=x,
∴
故答案为.
点睛:此题主要考查了解直角三角形的性质,关键是设出未知数表示出相应的线段的长,从而求比值.
17.30°
【详解】 ,则
18.∠BAC的度数为105°或15°.
【详解】试题分析:本题考查解直角三角形,由于题目没有给出△ABC的形状,所以要将∠BAC分为钝角和锐角进行分类分析,可过点A作AD⊥BC,在Rt△ADB中,结合已知的条件可求出∠BAD和AD, 在Rt△ADC中,结合已知条件AD和AC,利用锐角三角函数可求出∠CAD,再结合图形求出∠BAC.
解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D.在Rt△ABD中,∵∠B=30°,
∴∠BAD=60°,AD=AB·sin 30°=1.
在Rt△ACD中,CD===1,
∴△ACD是等腰直角三角形,则∠CAD=45°,
∴∠BAC=∠BAD+∠CAD=60°+45°=105°.
(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D.
∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°.
∴CD===1,
∴∠DAC=45°,
∴∠BAC=∠BAD-∠DAC=60°-45°=15°.
综上可知,∠BAC的度数为105°或15°.
常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解.
19.,
【分析】由正切的三角函数的定义即可求得∠A的正切值,从而可求得这个角的度数,进而可求得∠B的度数.
【详解】Rt △ABC 中, ∠C=90° ,
∵
∴
∴∠B=90゜ -∠A=60゜
【点睛】本题考查了正切函数的定义,特殊角的三角函数值,直角三角形的性质,关键是求得∠A的正切值.
20.(1),,;(2),,
【分析】(1)利用勾股定理求出b,根据tanA==1,求出∠A即可解决问题.
(2)利用勾股定理求出c,根据tanA==,求出∠A即可解决问题.
【详解】解:(1)b=,
tanA==1,
∴∠A=45°,
∴∠B=90°-45°=45°;
(2)c=,
tanA==,
∴∠A=30°,∠B=90°-30°=60°.
【点睛】本题考查了解直角三角形,掌握勾股定理和直角三角形的边角间关系是解决本题的关键.
21.,,
【分析】本题考查的是解直角三角形的相关计算,先求解,结合角平分线的定义可得,可得的大小,再求解,即可.
【详解】解:在中,
∵,,,
∴,
∴.
∵平分,
∴,
∴.
∵,
∴.
∵,
∴.
22.(1);(2)3.
【分析】(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:,再由AB=,得AC=2,则CE=1,从而得出BE.
【详解】(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=;
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB==,
设CE=x(x>0),则AE=x,则,
∴CE=x=1,AC=2,
在Rt△ABC中,,
∵AB=2CD=,
∴BC=4,
∴BE=BC﹣CE=3.
23.(1);(2)4
【详解】解:(1)如图,连结
∵AD是⊙O的切线 ∴
设,则,,
∴
∴
∴
(2)解:,.
∴.
∴.
在Rt中,
∴⊙O的半径是4.
24.(1)见解析;(2)
【分析】(1)证明AD=AB且∠BAD=60 即可得到结论;
(2)证明△EGF是直角三角形,再运用勾股定理求解即可.
【详解】(1)证明:∵,
∴.
∴,∴是等边三角形.
(2)解:为的中点,
∴.
∵是等边三角形,,
∴,
∴.
又∵,
∴,
∴.
∴△EGF是直角三角形,
又∵,
∴∠BFG=90
∴∠FBG=30 ,
∴,
∴,
∴.
【点睛】此题主要考查了等边三角形的判定与性质,勾股定理以及解直角三角形,熟练掌握相关的判定与性质是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.5解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,等边ABC的边长为3,点D在边AC上,AD=,线段PQ在边BA上运动,PQ=,则四边形PCDQ面积的最大值为( )
A. B. C. D.
2.已知在中,,,则的值为( )
A. B. C. D.
3.在△ABC中,∠C=90°,且已知b和∠B,下列求c的表达式正确的是( )
A.c=bcosB B.c=bsinB C.c= D.c=
4.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. B. C. D.
5.如图,是用12个相似的直角三角形组成的图案.若,则的长度为( )
A. B. C. D.
6.如图,线杆DC的高度为,两根拉线与互相垂直,,若、、在同一条直线上,则拉线的长度为( )
A. B. C. D.
7.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
8.如图所示,平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成60°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长( )
A. B. C. D.
9.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100 B.200 C.100 D.200
10.如图,在中,,D是上一点,连结,若,则的长可表示为( )
A. B. C. D.
11.如图,延长等腰斜边到,使,连接,则的值为( )
A. B.1 C. D.
12.等腰三角形的两条边长分别是4 cm、9 cm,则等腰三角形的底角的余弦值是( )
A. B. C. D.
二、填空题
13.如图,是内一点,,,,,则的长为 .
14.如图,已知半的直径为3,弦与弦交于点,,垂足为点,,则弦的长为 .
15.四边形ABCD中,∠C=90°,AB=12,BC=4,CD=3,AD=13,则四边形ABCD的面积为 .
16.如图,在Rt△ABD中,∠A=90°,点C在AD上,∠ACB=45°,tan∠D=,则=
17.在Rt△ABC中,∠C=90°,BC=,AB=,则∠B= .
三、解答题
18.在△ABC中,AB=2,AC=,∠B=30°.求∠BAC的度数.
19.在Rt中,,,,求,的度数.
20.在中,,所对的边分别为a,b,c,根据下列条件求出直角三角形的其他元素:
(1);
(2).
21.如图,在中,,,的平分线,求的度数及边,的长.
22.如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=,求BE的值.
23.如图,已知:内接于⊙O,是⊙O的切线,的延长线交于点.
(1)若∠B=2∠D ,求∠D的度数;
(2)在(1)的条件下,若,求⊙O的半径.
24.如图,在中,,,,垂足为G,且,E为的中点,.
(1)求证:是等边三角形.
(2)过点G作于点F,连接、,求的长.
《7.5解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C C C B D B B C
题号 11 12
答案 A C
1.C
【分析】设BP=x(x≥0),过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,利用正弦三角函数求得S△PBC ,S△ADQ,当两三角形的面积和最小时,四边形的面积最大,根据x≥0即可判断;
【详解】解:如图,过P作PE⊥BC于E点,过Q作QF⊥AC于F点,过C作CH⊥AB于H点,设BP=x(x≥0),则AQ=3--x=-x,
∵△ABC是等边三角形,∴∠A=∠B=60°,
∴,,,
∴S△PBC=,
S△ADQ,
S△ABC=,
S△PBC+S△ADQ=≥(x=0时,有最小值),
∴四边形PCDQ面积≤-=,
故选: C.
【点睛】,本题考查了正弦三角函数,等边三角形的性质,根据面积关系正确作出辅助线是解题关键.
2.D
【分析】根据正弦三角函数的定义,设,则,,再根据正切三角函数的定义,即可求解.
【详解】
∵在中,,,
∴,
设,则,,
∴,
故选:D.
【点睛】本题主要考查三角函数的定义,根据三角函数的定义,用未知数表示出直角三角形的各边长,是解题的关键.
3.C
【详解】试题解析:在中,,
故选C.
4.C
【分析】根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根据全等三角形的性质可得出OE=OB、EF=BP,设EF=x,则BP=x、DF=4﹣x、BF=PC=3﹣x,进而可得出AF=1+x,在Rt△DAF中,利用勾股定理可求出x的值,再利用余弦的定义即可求出cos∠ADF的值.
【详解】根据折叠,可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP.
设EF=x,则BP=x,DF=DE﹣EF=4﹣x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,
∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,
解得:x=,
∴DF=4﹣x=,
∴cos∠ADF=,
故选C.
【点睛】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合AF=1+x,求出AF的长度是解题的关键.
5.C
【分析】本题考查的是相似三角形的性质,锐角三角函数的应用,规律探究;
先求解,可得,再进一步探究即可;
【详解】解:∵12个相似的直角三角形,
∴,
,
∵,
∴,
,
,
∴,
故选:C
6.B
【分析】根据同角的余角相等得∠CAD=∠BCD,由,即可求出BC的长度.
【详解】解:∵两根拉线与互相垂直,DC垂直AB,
∴∠CAB+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAB=∠BCD,
∵,∴
在Rt△BCD中,;
∴
故选:B.
【点睛】本题主要考查解直角三角形,熟练掌握同角的余角相等和三角函数的定义是解题的关键.
7.D
【详解】试题分析:∵∠C=90°,∠A=40°,∴∠B=50°.
∵BC=3,,∴.
故选D.
考点:1.直角三角形两锐角的关系;2.锐角三角函数定义.
8.B
【详解】解:CD=BD-BC=.
故选B.
9.B
【详解】试题分析:根据方位角可得:∠A=30°,∠CBA=120°,则∠C=30°,则△ABC为等腰三角形,故BC=AB=200m,故选B.
10.C
【分析】利用锐角三角函数关系分别表示出的长进而得出答案.
【详解】解:∵,,
∴,
则,
,
故,
则,
故,
故选:C.
【点睛】此题主要考查了锐角三角函数的定义,正确掌握三角函数是解题关键.
11.A
【分析】过点D作DE垂直于CB的延长线于点E,设AC=BC=a,根据勾股定理得,由等腰直角三角形的性质得∠ABC=∠BAC=45°,从而得,在Rt△BDE中,解直角三角形得DE=2a,BE=2a,进而求得CE=BC+BE=3a即可求得.
【详解】解:过点D作DE垂直于CB的延长线于点E,如下图,
设AC=BC=a,
∵AC⊥BC,AC=BC=a,
∴,∠ABC+∠BAC=90°,∠ABC=∠BAC,
∴∠ABC=∠BAC=45°,,
∴∠DBE=∠ABC=45°,
∵DE⊥CE,
∴DE=,BE=,
∴CE=BC+BE=3a,
∴,
故选:A.
【点睛】本题主要考查了勾股定理,等腰直角三角形的性质,解直角三角形,熟练解直角三角形是解题的关键.
12.C
【分析】等腰三角形两边的长为4cm和9cm,题目没有明确说明哪条是底边,哪条是腰,因此要分两种情况讨论;
对每一种情况,还需利用三角形三边关系验证能否构成三角形,若能构成三角形,再根据等腰三角形的性质以及余弦的定义进一步解答即可得到答案.
【详解】①当腰长为4cm时,则另外两边长分别为4cm和9cm,
4+4=8<9,不满足三角形三边关系,即此三角形不存在;
②当腰长为9cm时,则另外两边长分别为9cm和4cm,满足三角形三边关系,如图,
过A作AD⊥BC,垂足为D.
∵ AB=AC AD⊥BC,
∴ BD=DC (三线合一),
∵ BD=DC ,BC=4,
∴ DC=2,
∵ AD⊥BC DC=2, AC=9,
∴ cos∠BCA= =,即等腰三角形的底角的余弦值是 .
故选C.
【点睛】本题考查等腰三角形和三角函数的知识,解答本题需掌握等腰三角形三线合一的性质以及余弦的定义.
13.
【分析】过点作的垂线,过点作的垂线,两垂线交于点,连接,证明,由相似三角形的性质得出,证明,得出,求出,由勾股定理求出AM,最后由直角三角形的性质可求出的长.
【详解】如图,过点作的垂线,过点作的垂线,两垂线交于点,连接,
,
,
,
,
又,
,
,
,
,即,
,
,
,
,
在中,,
.
【点睛】此题考查了解直角三角形,勾股定理,相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质是解题的关键.
14.
【分析】由AC=BD知 ,得 ,根据OD⊥AC知,从而得,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
【详解】∵OD⊥AC,
∴,∠AFO=90°,
又∵AC=BD,
∴,即,
∴,
∴,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=3,
∴AF=AOsin∠AOF=,
则AC=2AF=;
【点睛】本题考查圆心角,弧,弦之间的关系,解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
15.36
【分析】先根据勾股定理求出AC的长度,再根据勾股定理的逆定理判断出△ACD的形状,再利用三角形的面积公式求解即可.
【详解】如图,
∵∠C=90°CD=3,BC=4
∴BD===5
在△ABD中,AB2+BD2=25+144=169=AD2,
∴△ABD是直角三角形,
∴S四边形ABCD=AB BD+BC CD,
=×5×12+×3×4,
=36.
故答案为36
【点睛】本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键.
16.
【分析】先根据∠D的正切值设AB=2x,AD=3x,然后根据等腰直角三角形的性质求出CD的长,即可求解.
【详解】解:在Rt△ABD中,
∵
∴设AB=2x,AD=3x,
∵∠ACB=45°,
∴AC=AB=2x,
则CD=AD﹣AC=3x﹣2x=x,
∴
故答案为.
点睛:此题主要考查了解直角三角形的性质,关键是设出未知数表示出相应的线段的长,从而求比值.
17.30°
【详解】 ,则
18.∠BAC的度数为105°或15°.
【详解】试题分析:本题考查解直角三角形,由于题目没有给出△ABC的形状,所以要将∠BAC分为钝角和锐角进行分类分析,可过点A作AD⊥BC,在Rt△ADB中,结合已知的条件可求出∠BAD和AD, 在Rt△ADC中,结合已知条件AD和AC,利用锐角三角函数可求出∠CAD,再结合图形求出∠BAC.
解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D.在Rt△ABD中,∵∠B=30°,
∴∠BAD=60°,AD=AB·sin 30°=1.
在Rt△ACD中,CD===1,
∴△ACD是等腰直角三角形,则∠CAD=45°,
∴∠BAC=∠BAD+∠CAD=60°+45°=105°.
(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D.
∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°.
∴CD===1,
∴∠DAC=45°,
∴∠BAC=∠BAD-∠DAC=60°-45°=15°.
综上可知,∠BAC的度数为105°或15°.
常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解.
19.,
【分析】由正切的三角函数的定义即可求得∠A的正切值,从而可求得这个角的度数,进而可求得∠B的度数.
【详解】Rt △ABC 中, ∠C=90° ,
∵
∴
∴∠B=90゜ -∠A=60゜
【点睛】本题考查了正切函数的定义,特殊角的三角函数值,直角三角形的性质,关键是求得∠A的正切值.
20.(1),,;(2),,
【分析】(1)利用勾股定理求出b,根据tanA==1,求出∠A即可解决问题.
(2)利用勾股定理求出c,根据tanA==,求出∠A即可解决问题.
【详解】解:(1)b=,
tanA==1,
∴∠A=45°,
∴∠B=90°-45°=45°;
(2)c=,
tanA==,
∴∠A=30°,∠B=90°-30°=60°.
【点睛】本题考查了解直角三角形,掌握勾股定理和直角三角形的边角间关系是解决本题的关键.
21.,,
【分析】本题考查的是解直角三角形的相关计算,先求解,结合角平分线的定义可得,可得的大小,再求解,即可.
【详解】解:在中,
∵,,,
∴,
∴.
∵平分,
∴,
∴.
∵,
∴.
∵,
∴.
22.(1);(2)3.
【分析】(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:,再由AB=,得AC=2,则CE=1,从而得出BE.
【详解】(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=CH,
∴CH:AC=1:,
∴sinB=;
(2)∵sinB=,
∴AC:AB=1:,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB==,
设CE=x(x>0),则AE=x,则,
∴CE=x=1,AC=2,
在Rt△ABC中,,
∵AB=2CD=,
∴BC=4,
∴BE=BC﹣CE=3.
23.(1);(2)4
【详解】解:(1)如图,连结
∵AD是⊙O的切线 ∴
设,则,,
∴
∴
∴
(2)解:,.
∴.
∴.
在Rt中,
∴⊙O的半径是4.
24.(1)见解析;(2)
【分析】(1)证明AD=AB且∠BAD=60 即可得到结论;
(2)证明△EGF是直角三角形,再运用勾股定理求解即可.
【详解】(1)证明:∵,
∴.
∴,∴是等边三角形.
(2)解:为的中点,
∴.
∵是等边三角形,,
∴,
∴.
又∵,
∴,
∴.
∴△EGF是直角三角形,
又∵,
∴∠BFG=90
∴∠FBG=30 ,
∴,
∴,
∴.
【点睛】此题主要考查了等边三角形的判定与性质,勾股定理以及解直角三角形,熟练掌握相关的判定与性质是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
