6.3整式的乘法同步强化练习(含解析)
文档属性
| 名称 | 6.3整式的乘法同步强化练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 928.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-04 13:09:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3整式的乘法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
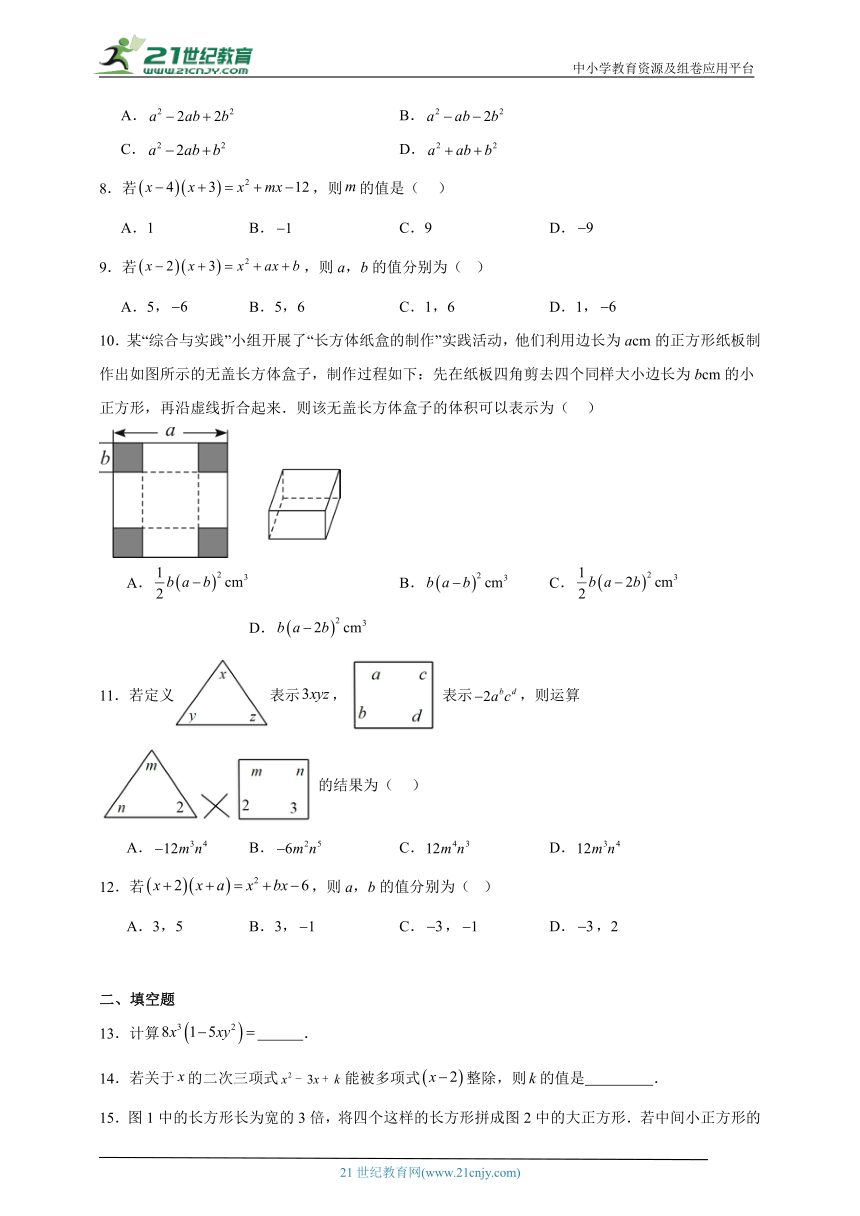
1.将两个边长分别为,a的正方形按如图和图所示的方式(两个正方形有一条边在同一直线上)放置在长为m,宽为n()的长方形内,设图,图中的阴影面积分别为,,则,的大小关系为( )
A. B. C. D.无法确定
2.下列计算正确的是( )
A. B. C. D.
3.若,则( )
A. B. C.2 D.4
4.下列运算正确的是( )
A. B. C. D.
5.老师在黑板上书写了一个正确的算式,随后用手掌遮住了一个多项式,形式如下:,则 处应为( )
A. B.
C. D.
6.计算的结果是( )
A. B. C. D.
7.一个长方形的隔离室,一边长为,另一边长为,则长方形的面积为( )
A. B.
C. D.
8.若,则的值是( )
A.1 B. C.9 D.
9.若,则a,b的值分别为( )
A.5, B.5,6 C.1,6 D.1,
10.某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为acm的正方形纸板制作出如图所示的无盖长方体盒子,制作过程如下:先在纸板四角剪去四个同样大小边长为bcm的小正方形,再沿虚线折合起来.则该无盖长方体盒子的体积可以表示为( )
A. B. C. D.
11.若定义表示,表示,则运算的结果为( )
A. B. C. D.
12.若,则a,b的值分别为( )
A.3,5 B.3, C., D.,2
二、填空题
13.计算 .
14.若关于的二次三项式能被多项式整除,则的值是 .
15.图1中的长方形长为宽的3倍,将四个这样的长方形拼成图2中的大正方形.若中间小正方形的面积是,问图1中的长方形的面积是 .
16.定义为二阶行列式,规定它的运算法则为,那么, .
17.如图,正方形ABCD是由正方形EFGH和四个形状、大小一样的直角三角形组成.若阴影部分的面积等于的面积,则阴影部分与正方形ABCD的面积比值为 .
三、解答题
18.计算:
(1)
(2)
19.已知,求单项式A.
20.有这样一道题:“计算:”,小宇同学在解题时错误地把第一个多项式中的“”写成了“”,得到的结果为.
(1)求a,b的值;
(2)请你写出这道整式乘法题的正确运算结果.
21.计算:
(1);
(2).
22.计算:
(1);
(2);
(3);
(4);
(5);
(6).
23.计算题.
(1).
(2).
24.计算:
(1);
(2);
(3);
(4).
《6.3整式的乘法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D C C A B B D D
题号 11 12
答案 A C
1.A
【分析】利用面积的和差分别表示出和,然后利用整式的混合运算计算它们的差即可.
【详解】解:根据题意得:;
,
∴
∵
∴
∴
∴
∴
故选:A.
【点睛】本题考查了整式的混合运算:整体"思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看作整体的代数式通常要用括号括起来.也考查了正方形的性质.
2.A
【分析】本题考查了整式的运算,根据积的乘方运算、幂的乘方、合并同类项、同底数幂的乘法的运算规则进行计算即可判断,掌握整式的运算法则是解题的关键.
【详解】、,故该选项正确,符合题意;
、,故该选项错误,不符合题意;
、,故该选项错误,不符合题意;
、,故该选项错误,不符合题意;
故选:.
3.D
【分析】根据多项式乘以多项式展开,根据常数项相等得出,进而根据一次项系数相等得出,代入代数式,即可求解.
【详解】解:∵
∵
∴,
解得:,
∴,
故选:D.
【点睛】本题考查了多项式乘以多项式,熟练掌握多项式乘以多项式的运算法则是解题的关键.
4.C
【分析】A不是同类项,不能合并,B根据同底数幂除法法则计算即可,C根据幂的乘方运算法则计算即可,D根据单项式和同底数幂相乘运算法则计算即可.
【详解】A、,不是同类项,不能合并,故错误
B、,故错误
C、,故正确
D、,故错误
故选:C.
【点睛】本题主要考查了合并同类项,同底数幂除法,幂的乘方,同底数幂相乘,熟练掌握以上运算法则是解题的关键.
5.C
【分析】本题考查了整式的乘除法,直接利用整式的乘法运算法则计算得出答案即可.
【详解】解:由题意得:.
故选:C.
6.A
【分析】本题考查了单项式的乘法运算,先进行乘方运算,再进行乘法运算即可求解.
【详解】解:.
故选:A.
7.B
【分析】根据长方形的面积公式列出算式,按多项式乘以多项式的法则计算即可解答.
【详解】解:根据题意得,长方形的面积为:
;
故选:B.
【点睛】本题考查多项式乘以多项式的法则,即把第一个多项式的每一项分别乘以第二个多项式的每一项,再把所得的积相加,熟练运用这一法则是解题的关键.
8.B
【分析】根据多项式乘多项式的计算法则计算出即可求解.
【详解】解:∵
∴,
∴,
故选:B.
【点睛】本题主要考查了多项式乘以多项式,解题的关键在于能够熟练掌握多项式乘多项式的计算法则.
9.D
【分析】已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件即可求出a与b的值.
【详解】解:∵,
∴,,故D正确.
故选:D.
【点睛】本题主要考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
10.D
【分析】根据分别用代数式表示长方体的长、宽、高,利用体积计算公式可得答案.
【详解】解:由题意得,这个长方体的底面是边长为(a-2b)的正方形,高为b,
所以体积为(a-2b)(a-2b)×b=b(a-2b)2(cm3),
故选:D.
【点睛】本题考查认识立体图形,列代数式,整式乘法,掌握长方体体积的计算方法是正确解答的关键.
11.A
【分析】根据新定义列出算式进行计算,即可得出答案.
【详解】解:根据定义得:
=3×m×n×2×(-2)×m2×n3
=-12m3n4,
故选:A.
【点睛】本题考查了整式的混合运算,根据新定义列出算式是解决问题的关键.
12.C
【分析】本题考查的是整式的乘法运算,熟练的利用多项式乘以多项式的法则进行运算是解本题的关键.先按照多项式乘以多项式的法则进行计算,再利用多项式的恒等进行比较即可.
【详解】解:∵,
∴,,
∴,
∴.
故选:C.
13.
【分析】本题主要考查单项式乘多项式,根据单项式乘多项式法则进行计算即可.
【详解】,
故答案为:.
14.2
【分析】设二次三项式除以多项式的商式为(x+m),则=(x+m),再按多项式法则展开,即可求解.
【详解】解:设二次三项式能被多项式的商式为(x+m),则
=(x+m)=x2+(m-2)x-2m,
∴,解得:,
故答案为:2.
【点睛】本题考查多项式乘以多项式法则,熟练掌握多项式乘以多项式法则是解题的关键.
15.
【分析】设长方形的长为x,宽为3x,根据图2可知,进而即可求解;
【详解】解:设长方形的长为x,宽为3x;
根据图2可知,,
解得:,
所以图1中的长方形的面积是:.
故答案为:.
【点睛】本题主要考查列整式方程,根据题图列出方程是解题的关键.
16./
【分析】根据,列式计算即可求解.
【详解】解:
.
故答案为:.
【点睛】本题考查整式的混合运算,解答本题的关键是明确题目中的新规定,会用新规定解答问题.
17.
【分析】连接BG,设BF=a,EF=b,可用含a、b的代数式分别表示阴影部分的面积和的面积,由于阴影部分的面积等于的面积,可得,再用含a的代数式表示阴影部分的面积和正方形ABCD的面积,即可求解.
【详解】解:连接BG,设BF=a,EF=b,
则,,
∵阴影部分的面积等于的面积,
∴,即,
∴,
正方形ABCD的面积为:,
∴阴影部分与正方形ABCD的面积比为:,
即比值为:,
故答案为:.
【点睛】本题考查列代数式,正确表示出三角形和小正方形的面积是解题的关键.
18.(1)
(2)
【分析】(1)根据单项式乘多项式法则:分别用单项式乘多项式中的每一项,再把所得的积相加即可求解;
(2)根据多项式乘多项式的法则:多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了单项式乘多项式,多项式乘多项式,掌握单项式乘多项式,多项式乘多项式的法则是解题的关键.
19..
【分析】由乘法的意义可得,再利用积的乘方运算的逆运算可得答案.
【详解】解:∵,
∴,
∴;
【点睛】本题考查的是单项式的乘法与单项式的除法运算,积的乘方运算的逆运算,熟记运算法则是解本题的关键.
20.(1),
(2)
【分析】本题考查了多项式乘多项式,解二元一次方程,熟练掌握多项式乘多项式的法则是解决本题的关键.
(1)根据题意可得,应用多项式乘多项式的法则进行计算,可得,由已知常数项相等可得,计算即可得出答案;
(2)由(1)可知a、b的值,代入应用多项式乘多项式进行计算即可得出答案.
【详解】(1)解:
,
由题意可知,上式,
∴,,
解得:,.
(2)解:
.
21.(1)
(2)
【分析】本题考查了整式的混合运算.
(1)先算积的乘方,再按照单项式乘单项式的计算方法计算;
(2)首先计算乘方,再计算单项式的乘法,最后合并即可.
【详解】(1)解:
;
(2)解:
.
22.(1)
(2)
(3)
(4)
(5)
(6)
【分析】(1)利用多项式乘以多项式的法则进行运算即可得到答案;
(2)利用多项式乘以多项式的法则进行运算即可得到答案;
(3)利用多项式乘以多项式的法则进行运算即可得到答案;
(4)利用多项式乘以多项式的法则进行运算即可得到答案;
(5)利用多项式乘以多项式的法则进行运算即可得到答案;
(6)利用多项式乘以多项式的法则进行运算即可得到答案.
【详解】(1);
(2);
(3);
(4);
(5);
(6)
【点睛】本题考查的是多项式乘以多项式,掌握“多项式乘以多项式的法则:把一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加”是解题的关键.
23.(1)
(2)
【分析】本题考查了整式的混合运算,熟练掌握运算法则是解答本题的关键.
(1)先计算积得乘方,再按单项式的乘法法则运算即可;
(2)先计算积得乘方,再按单项式的乘除法则运算即可.
【详解】(1)原式
.
(2)原式
.
24.(1)
(2)
(3)
(4)
【分析】此题考查了多项式乘以多项式运算,解题的关键是掌握多项式乘以多项式运算法则.
(1)利用多项式乘以多项式运算法则求解即可;
(2)利用多项式乘以多项式运算法则求解即可;
(3)利用多项式乘以多项式运算法则求解即可;
(4)利用多项式乘以多项式运算法则求解即可.
【详解】(1)
;
(2)
;
(3)
;
(4)
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3整式的乘法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将两个边长分别为,a的正方形按如图和图所示的方式(两个正方形有一条边在同一直线上)放置在长为m,宽为n()的长方形内,设图,图中的阴影面积分别为,,则,的大小关系为( )
A. B. C. D.无法确定
2.下列计算正确的是( )
A. B. C. D.
3.若,则( )
A. B. C.2 D.4
4.下列运算正确的是( )
A. B. C. D.
5.老师在黑板上书写了一个正确的算式,随后用手掌遮住了一个多项式,形式如下:,则 处应为( )
A. B.
C. D.
6.计算的结果是( )
A. B. C. D.
7.一个长方形的隔离室,一边长为,另一边长为,则长方形的面积为( )
A. B.
C. D.
8.若,则的值是( )
A.1 B. C.9 D.
9.若,则a,b的值分别为( )
A.5, B.5,6 C.1,6 D.1,
10.某“综合与实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为acm的正方形纸板制作出如图所示的无盖长方体盒子,制作过程如下:先在纸板四角剪去四个同样大小边长为bcm的小正方形,再沿虚线折合起来.则该无盖长方体盒子的体积可以表示为( )
A. B. C. D.
11.若定义表示,表示,则运算的结果为( )
A. B. C. D.
12.若,则a,b的值分别为( )
A.3,5 B.3, C., D.,2
二、填空题
13.计算 .
14.若关于的二次三项式能被多项式整除,则的值是 .
15.图1中的长方形长为宽的3倍,将四个这样的长方形拼成图2中的大正方形.若中间小正方形的面积是,问图1中的长方形的面积是 .
16.定义为二阶行列式,规定它的运算法则为,那么, .
17.如图,正方形ABCD是由正方形EFGH和四个形状、大小一样的直角三角形组成.若阴影部分的面积等于的面积,则阴影部分与正方形ABCD的面积比值为 .
三、解答题
18.计算:
(1)
(2)
19.已知,求单项式A.
20.有这样一道题:“计算:”,小宇同学在解题时错误地把第一个多项式中的“”写成了“”,得到的结果为.
(1)求a,b的值;
(2)请你写出这道整式乘法题的正确运算结果.
21.计算:
(1);
(2).
22.计算:
(1);
(2);
(3);
(4);
(5);
(6).
23.计算题.
(1).
(2).
24.计算:
(1);
(2);
(3);
(4).
《6.3整式的乘法》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D C C A B B D D
题号 11 12
答案 A C
1.A
【分析】利用面积的和差分别表示出和,然后利用整式的混合运算计算它们的差即可.
【详解】解:根据题意得:;
,
∴
∵
∴
∴
∴
∴
故选:A.
【点睛】本题考查了整式的混合运算:整体"思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看作整体的代数式通常要用括号括起来.也考查了正方形的性质.
2.A
【分析】本题考查了整式的运算,根据积的乘方运算、幂的乘方、合并同类项、同底数幂的乘法的运算规则进行计算即可判断,掌握整式的运算法则是解题的关键.
【详解】、,故该选项正确,符合题意;
、,故该选项错误,不符合题意;
、,故该选项错误,不符合题意;
、,故该选项错误,不符合题意;
故选:.
3.D
【分析】根据多项式乘以多项式展开,根据常数项相等得出,进而根据一次项系数相等得出,代入代数式,即可求解.
【详解】解:∵
∵
∴,
解得:,
∴,
故选:D.
【点睛】本题考查了多项式乘以多项式,熟练掌握多项式乘以多项式的运算法则是解题的关键.
4.C
【分析】A不是同类项,不能合并,B根据同底数幂除法法则计算即可,C根据幂的乘方运算法则计算即可,D根据单项式和同底数幂相乘运算法则计算即可.
【详解】A、,不是同类项,不能合并,故错误
B、,故错误
C、,故正确
D、,故错误
故选:C.
【点睛】本题主要考查了合并同类项,同底数幂除法,幂的乘方,同底数幂相乘,熟练掌握以上运算法则是解题的关键.
5.C
【分析】本题考查了整式的乘除法,直接利用整式的乘法运算法则计算得出答案即可.
【详解】解:由题意得:.
故选:C.
6.A
【分析】本题考查了单项式的乘法运算,先进行乘方运算,再进行乘法运算即可求解.
【详解】解:.
故选:A.
7.B
【分析】根据长方形的面积公式列出算式,按多项式乘以多项式的法则计算即可解答.
【详解】解:根据题意得,长方形的面积为:
;
故选:B.
【点睛】本题考查多项式乘以多项式的法则,即把第一个多项式的每一项分别乘以第二个多项式的每一项,再把所得的积相加,熟练运用这一法则是解题的关键.
8.B
【分析】根据多项式乘多项式的计算法则计算出即可求解.
【详解】解:∵
∴,
∴,
故选:B.
【点睛】本题主要考查了多项式乘以多项式,解题的关键在于能够熟练掌握多项式乘多项式的计算法则.
9.D
【分析】已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件即可求出a与b的值.
【详解】解:∵,
∴,,故D正确.
故选:D.
【点睛】本题主要考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
10.D
【分析】根据分别用代数式表示长方体的长、宽、高,利用体积计算公式可得答案.
【详解】解:由题意得,这个长方体的底面是边长为(a-2b)的正方形,高为b,
所以体积为(a-2b)(a-2b)×b=b(a-2b)2(cm3),
故选:D.
【点睛】本题考查认识立体图形,列代数式,整式乘法,掌握长方体体积的计算方法是正确解答的关键.
11.A
【分析】根据新定义列出算式进行计算,即可得出答案.
【详解】解:根据定义得:
=3×m×n×2×(-2)×m2×n3
=-12m3n4,
故选:A.
【点睛】本题考查了整式的混合运算,根据新定义列出算式是解决问题的关键.
12.C
【分析】本题考查的是整式的乘法运算,熟练的利用多项式乘以多项式的法则进行运算是解本题的关键.先按照多项式乘以多项式的法则进行计算,再利用多项式的恒等进行比较即可.
【详解】解:∵,
∴,,
∴,
∴.
故选:C.
13.
【分析】本题主要考查单项式乘多项式,根据单项式乘多项式法则进行计算即可.
【详解】,
故答案为:.
14.2
【分析】设二次三项式除以多项式的商式为(x+m),则=(x+m),再按多项式法则展开,即可求解.
【详解】解:设二次三项式能被多项式的商式为(x+m),则
=(x+m)=x2+(m-2)x-2m,
∴,解得:,
故答案为:2.
【点睛】本题考查多项式乘以多项式法则,熟练掌握多项式乘以多项式法则是解题的关键.
15.
【分析】设长方形的长为x,宽为3x,根据图2可知,进而即可求解;
【详解】解:设长方形的长为x,宽为3x;
根据图2可知,,
解得:,
所以图1中的长方形的面积是:.
故答案为:.
【点睛】本题主要考查列整式方程,根据题图列出方程是解题的关键.
16./
【分析】根据,列式计算即可求解.
【详解】解:
.
故答案为:.
【点睛】本题考查整式的混合运算,解答本题的关键是明确题目中的新规定,会用新规定解答问题.
17.
【分析】连接BG,设BF=a,EF=b,可用含a、b的代数式分别表示阴影部分的面积和的面积,由于阴影部分的面积等于的面积,可得,再用含a的代数式表示阴影部分的面积和正方形ABCD的面积,即可求解.
【详解】解:连接BG,设BF=a,EF=b,
则,,
∵阴影部分的面积等于的面积,
∴,即,
∴,
正方形ABCD的面积为:,
∴阴影部分与正方形ABCD的面积比为:,
即比值为:,
故答案为:.
【点睛】本题考查列代数式,正确表示出三角形和小正方形的面积是解题的关键.
18.(1)
(2)
【分析】(1)根据单项式乘多项式法则:分别用单项式乘多项式中的每一项,再把所得的积相加即可求解;
(2)根据多项式乘多项式的法则:多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了单项式乘多项式,多项式乘多项式,掌握单项式乘多项式,多项式乘多项式的法则是解题的关键.
19..
【分析】由乘法的意义可得,再利用积的乘方运算的逆运算可得答案.
【详解】解:∵,
∴,
∴;
【点睛】本题考查的是单项式的乘法与单项式的除法运算,积的乘方运算的逆运算,熟记运算法则是解本题的关键.
20.(1),
(2)
【分析】本题考查了多项式乘多项式,解二元一次方程,熟练掌握多项式乘多项式的法则是解决本题的关键.
(1)根据题意可得,应用多项式乘多项式的法则进行计算,可得,由已知常数项相等可得,计算即可得出答案;
(2)由(1)可知a、b的值,代入应用多项式乘多项式进行计算即可得出答案.
【详解】(1)解:
,
由题意可知,上式,
∴,,
解得:,.
(2)解:
.
21.(1)
(2)
【分析】本题考查了整式的混合运算.
(1)先算积的乘方,再按照单项式乘单项式的计算方法计算;
(2)首先计算乘方,再计算单项式的乘法,最后合并即可.
【详解】(1)解:
;
(2)解:
.
22.(1)
(2)
(3)
(4)
(5)
(6)
【分析】(1)利用多项式乘以多项式的法则进行运算即可得到答案;
(2)利用多项式乘以多项式的法则进行运算即可得到答案;
(3)利用多项式乘以多项式的法则进行运算即可得到答案;
(4)利用多项式乘以多项式的法则进行运算即可得到答案;
(5)利用多项式乘以多项式的法则进行运算即可得到答案;
(6)利用多项式乘以多项式的法则进行运算即可得到答案.
【详解】(1);
(2);
(3);
(4);
(5);
(6)
【点睛】本题考查的是多项式乘以多项式,掌握“多项式乘以多项式的法则:把一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加”是解题的关键.
23.(1)
(2)
【分析】本题考查了整式的混合运算,熟练掌握运算法则是解答本题的关键.
(1)先计算积得乘方,再按单项式的乘法法则运算即可;
(2)先计算积得乘方,再按单项式的乘除法则运算即可.
【详解】(1)原式
.
(2)原式
.
24.(1)
(2)
(3)
(4)
【分析】此题考查了多项式乘以多项式运算,解题的关键是掌握多项式乘以多项式运算法则.
(1)利用多项式乘以多项式运算法则求解即可;
(2)利用多项式乘以多项式运算法则求解即可;
(3)利用多项式乘以多项式运算法则求解即可;
(4)利用多项式乘以多项式运算法则求解即可.
【详解】(1)
;
(2)
;
(3)
;
(4)
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
