期末测试(试题)-2024-2025学年五年级下册数学人教版(含解析)
文档属性
| 名称 | 期末测试(试题)-2024-2025学年五年级下册数学人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 220.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 17:30:38 | ||
图片预览




文档简介
期末测试
一、选择题
1.一个数既是21的因数,又是21的倍数,这个数是( )。
A.1 B.3 C.7 D.21
2.最小的质数是( )。
A.2 B.3 C.4 D.1
3.下面适合用折线统计图表示的是( )。
A.小林0~18岁身高变化情况 B.阳光小学五年级各班人数情况
C.学校图书馆各类图书数量情况 D.甲、乙、丙、丁四个城市三月份平均气温情况
4.把20克糖放入180克水中,糖占糖水的( )。
A. B. C. D.
5.把一个长方体切成几个小长方体后,表面积( )。
A.不变 B.比原来大 C.比原来小
6.下面两个数是互质数的是( )。
A.3和12 B.4和6 C.5和21 D.7和42
7.如果小刚的体重是小东的,小明的体重是小东的,下面说法正确的是( )。
A.小刚比小明重 B.小明比小刚重 C.无法比较
8.在下图□中填上合适的分数,□中的分数是( )。
A. B. C. D.
9.一个长方体的底面是一个面积为16cm2的正方形,它的侧面展开图也是一个正方形。这个长方体的体积是( )cm3。
A.16 B.64 C.128 D.256
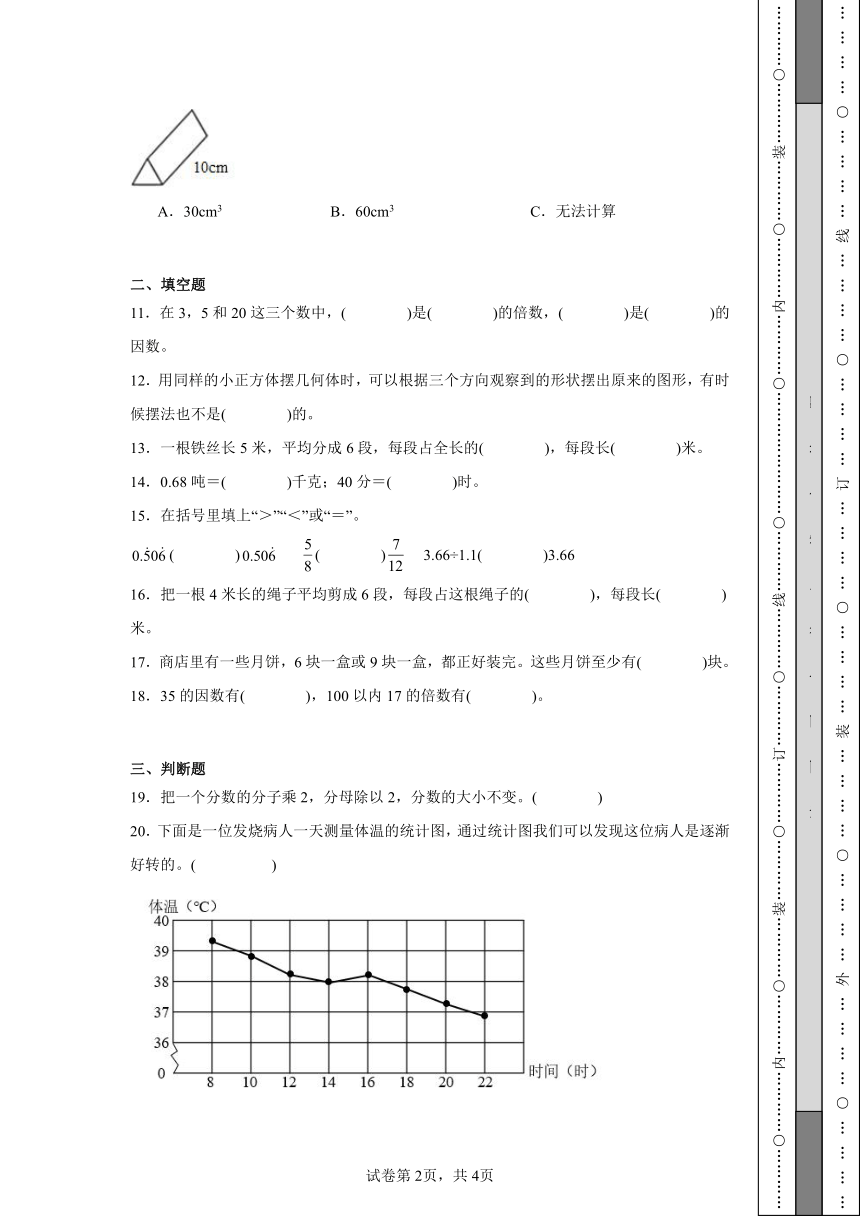
10.一个几何体如图,其中三角形面积为6cm2,它的体积是( )。
A.30cm3 B.60cm3 C.无法计算
二、填空题
11.在3,5和20这三个数中,( )是( )的倍数,( )是( )的因数。
12.用同样的小正方体摆几何体时,可以根据三个方向观察到的形状摆出原来的图形,有时候摆法也不是( )的。
13.一根铁丝长5米,平均分成6段,每段占全长的( ),每段长( )米。
14.0.68吨=( )千克;40分=( )时。
15.在括号里填上“>”“<”或“=”。
( ) ( ) 3.66÷1.1( )3.66
16.把一根4米长的绳子平均剪成6段,每段占这根绳子的( ),每段长( )米。
17.商店里有一些月饼,6块一盒或9块一盒,都正好装完。这些月饼至少有( )块。
18.35的因数有( ),100以内17的倍数有( )。
三、判断题
19.把一个分数的分子乘2,分母除以2,分数的大小不变。( )
20.下面是一位发烧病人一天测量体温的统计图,通过统计图我们可以发现这位病人是逐渐好转的。( )
21.一个病人打一次点滴的药水约是200升。( )
22.一块巧克力两人分,每人分到。( )
23.体积不相等的物体表面积一定不相等。( )
四、计算题
24.脱式计算。
(1) (2)
25.计算下列各题,怎样简便就怎样算。
五、解答题
26.王奶奶家养了10只鸡,养了7只鸭。鸭的数量是鸡的几分之几?
27.下图是实验小组的同学们测量珊瑚石体积的实验,请你用给出的数据计算珊瑚石的体积?
28.王芳做语文作业用了小时,做数学作业比语文作业少用了小时,她做数学作业用了多少小时?
29.一个长方体水槽,从里面量长、宽都是2分米,向水槽中倒入5.5升水,再把一块土豆放入水槽中,土豆完全浸没,这时量得水槽内水深15厘米,水没有溢出,这块土豆的体积是多少立方分米?
30.红星小区修建了一个长25米、宽20米、高1.8米的游泳池,给这个游泳池内部贴上瓷砖,需要多少平方米瓷砖?
31.一个长方体饼干盒,长17厘米,宽11厘米,高20厘米。如果在它的侧面贴满一圈包装纸(如图),包装纸的面积至少有多少平方厘米?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
《期末测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A A A B C A C D B
1.D
【分析】根据找一个数的因数的方法:一个数的因数是有限的,最大的因数是它本身,最小的因数是1;根据找一个数的倍数的方法,一个数的倍数是无限的,最小的一个倍数是它本身,可见一个数的本身既是其最大因数又是其最小倍数。
【详解】由分析可知:
一个数既是21的因数,又是21的倍数,这个数是21。
故答案为:D
2.A
【分析】一个数的因数只有1和本身,那么它是质数,2是最小的质数。
【详解】最小的质数是2。
故答案为:A
【点睛】本题考查了质数,掌握质数的概念是解题的关键。
3.A
【分析】条形统计图以直条长短清晰表示各数据大小,无需复杂转换或计算,一眼就能判断数量多少;折线统计图能通过折线的上升或下降,清晰直观地展现数据是增加还是减少,通过折线统计图可一目了然看出走势。
【详解】A.小林0~18岁身高变化,需体现随时间推移身高的增减变化趋势,折线统计图通过连接数据点形成折线,能直观清晰地展示这种变化,所以该情况适合用折线统计图;
B.阳光小学五年级各班人数,重点在于直观呈现各班人数具体数值的多少,条形统计图以直条长短表示数量,在比较数量多少方面更具优势,因此该情况适合条形统计图而非折线统计图。
C.学校图书馆各类图书数量,主要是对比不同类别图书数量的多少,条形统计图能清晰展示数量差异,更契合此需求,不适合用折线统计图。
D.四个城市三月份平均气温,是要对同一时间不同城市的气温数值进行比较,条形统计图在呈现数量多少对比上更清晰明了,所以该情况更适合条形统计图 。
故答案为:A
4.A
【分析】糖是20克,糖水是(20+180)克,求糖占糖水的几分之几,实际是求一个数占另一个数的几分之几,用20除以(20+180)即可得解。
【详解】20÷(20+180)
=20÷200
=
故答案为:A
【点睛】此题的解题关键是根据分数的意义,掌握求一个数占另一个数的几分之几的计算方法。
5.B
【分析】表面积:物体露在外面的面积和,是物体的表面积,由于将长方体分成几个小长方体后,立体图形的面的数量增加,表面积相应的增大了,据此选择。
【详解】根据分析得,把一个长方体切成几个小长方体后,表面积比原来大。
故答案为:B
【点睛】本题考查了长方体的表面积,对立体图形表面积有清晰的认识是解题的关键。
6.C
【分析】公因数只有1的两个数,叫做互质数,如:5和7是互质数,7和13也是互质数,据此解答。
【详解】A.3和12的公因数有1,3,所以3和12不是互质数;
B.4和6的公因数有1,2,所以4和6不是互质数;
C.5和21只有公因数1,所以5和21是互质数;
D.7和42的公因数有1,7,所以7和42不是互质数。
故答案为:C
【点睛】掌握互质数的意义是解答题目的关键。
7.A
【分析】由题意可知,小刚的体重和小明的体重都和小东的体重有关。小刚的体重是小东的,小明的体重是小东的,可将分数转化成小数,比较大小,据此解答。
【详解】,
小刚的体重可表示为:小东的体重×0.75
小明的体重可表示为:小东的体重×0.6
0.75>0.6,所以,小刚比小明重。
故答案为:A
8.C
【分析】观察图可知:数轴中的每个大格表示0.1,平均分成10个小格,每一小格代表的数值为0.1的,据此在数轴上表示出题目中相应的分数即可。
【详解】由分析可得:□中的分数是;
故答案为:C
【点睛】掌握分数的意义是解题的关键。
9.D
【分析】由题意可知,长方体的长和宽都是4cm,它的高等于底面周长,根据,可求出高,再根据,代入数据计算即可。
【详解】
(cm3)
一个长方体的底面是一个面积为16cm2的正方形,它的侧面展开图也是一个正方形。这个长方体的体积是256cm3。
故答案为:D
10.B
【分析】图示的几何体和长方体、正方体有相似处,都是上下粗细一样大的柱体,根据长方体、正方体的体积公式V=Sh可知,这个几何体的体积也是V=Sh,代入数据计算即可。
【详解】6×10=60(cm3)
故答案为:B
【点睛】关键是由长方体、正方体的体积公式推出几何体的体积公式。
11. 20 5 5 20
【分析】在整数除法中,商是整数且没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,据此填空即可。
【详解】因为20÷5=4,所以20是5的倍数,5是20的因数。
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
12.唯一
【分析】一个几何体从正面、左面、上面看到的形状,只是从它的三个不同方向看到的,不能反映它的全貌,所以根据从三个方向观察到的形状摆出原来的图形,有时候有几种摆法。
【详解】用同样的小正方体摆几何体时,可以根据三个方向观察到的形状摆出原来的图形,有时候摆法也不是唯一的。
【点睛】本题考查根据从不同方向观察几何体的平面图形还原立体图形,培养学生的空间想象力。
13.
【分析】先把这根铁丝看成单位“1”,平均分成6段,那么每段都是这根铁丝的;
这根铁丝总共5米长,每一段铁丝的长度就是米。
【详解】
(米)
所以每段占全长的,每段长米。
【点睛】考查分数的意义,重点是能够区分有单位的分数与没单位的分数的区别。
14. 680
【分析】(1)1吨=1000千克,高级单位转化成低级单位乘进率即可;
(2)1时=60分,低级单位转化成高级单位除以进率即可。
【详解】(1)0.68×1000=680(千克)
0.68吨=680千克
(2)40÷60=(时)
40分=时
15. < > <
【分析】将循环小数写成一般形式,再根据小数的大小比较方法,填出第一空;
将和先通分,再按照同分母分数的大小比较方法,比较大小,填出第二空;
一个数(0除外)除以一个大于1的数,商比原来的数小,据此填出第四空。
【详解】=0.506506…,=0.50666…,所以<;
=,=,所以>;
1.1>1,所以3.66÷1.1<3.66。
【点睛】本题考查了循环小数大小比较、分数大小比较以及商和被除数的关系,属于基础题,分析时需细心。
16.
【分析】把这条绳子的全长看作单位“1”,把“1”平均分成6段,用1除以6,即是每段占这根据绳子的几分之几,计算结果不带单位;
把4米长的绳子平均分成6段,用这根绳子的长度除以6,即是每段的长度,计算结果带单位。
【详解】1÷6=
4÷6=(米)
每段占这根绳子的,每段长米。
17.18
【分析】由题意可知,这些月饼的个数既是6的倍数,又是9的倍数时,刚好可以装完,求月饼的最少个数就是求这两个数的最小公倍数,据此解答。
【详解】
6和9的最小公倍数为:3×2×3=18
所以,这些月饼至少有18块。
【点睛】本题主要考查最小公倍数的应用,掌握求两个数最小公倍数的方法是解答题目的关键。
18. 1、5、7、35 17、34、51、68、85
【分析】根据求一个数因数和倍数的方法,分别求出35的因数及100 以内17的倍数即可。
【详解】35的因数有:1、5、7、35;
100以内17的倍数有:17、34、51、68、85。
【点睛】本题考查因数和倍数,明确求一个数的因数和倍数的方法是解题的关键。
19.×
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
【详解】把一个分数的分子乘2,分母也应乘2,分数的大小不变。
原题说法错误。
故答案为:×
【点睛】本题考查分数的基本性质的灵活运用。
20.√
【分析】折线统计图可以通过折线的上升和下降表示数量的增减变化情况,统计图中横轴表示测量体温的时间,纵轴表示病人的体温,表示体温的折线呈下降趋势,说明病人的体温正在下降并趋于正常体温,据此解答。
【详解】观察折线统计图可知,发烧病人的体温逐渐下降并趋于正常体温,说明这位病人病情逐渐好转。
故答案为:√
【点睛】掌握折线统计图的特征是解答题目的关键。
21.×
【分析】容积单位有升和毫升,其中升是较大的容积单位,毫升是较小的容积单位。1升水大约能倒满5个一次性纸杯,1毫升水只有十几滴。根据生活经验可知:计量一个病人打一次点滴的药水要选用较小的容积单位。
【详解】一个病人打一次点滴的药水约是200毫升。
故答案为:×
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
22.×
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数,据此解答。
【详解】一块巧克力两人分,没有说平均分,所以每人不一定都分到。
故答案为:×
【点睛】本题考查了分数的意义,注意用分数表示必须要平均分。
23.×
【分析】根据长方体的表面积公式和长方体的体积公式,通过举例论证题目中的说法是否正确。假设1号长方体的长为4厘米,宽为3厘米,高为2厘米,2号长方体的长为8厘米,宽为2厘米,高为1厘米,利用长方体的表面积和体积公式求出它们的表面积和体积,据此判断。
【详解】1号长方体表面积:(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方厘米)
2号长方体表面积:(8×2+8×1+2×1)×2
=(16+8+2)×2
=26×2
=52(平方厘米)
1号长方体的体积:4×3×2=24(立方厘米)
2号长方体的体积:8×2×1=16(立方厘米)
可见两个长方体的表面积相等,但这两个长方体的体积不相等。
所以原题中“体积不相等的物体表面积一定不相等”的说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握立体图形表面积、体积的计算方法及应用。
24.;
【分析】第一题先通分,再按照四则运算顺序先计算减法,最后算加法;
第二题利用减法的性质进行简便计算即可。
【详解】
=
=
=
=
=
=
=
25.;;0
【分析】(1)利用加法交换律简便计算;
(2)利用加法交换律和结合律简便计算;
(3)先去掉小括号,再利用减法性质简便计算。
【详解】(1)
=
=
=
(2)
=
=
=
(3)
=
=
=
=0
26.
【分析】求一个数是另一个数的几分之几用除法计算,商用分数表示即可。
【详解】7÷10=
答:鸭的数量是鸡的。
27.562.5立方厘米
【分析】珊瑚石完全浸没在水里后,珊瑚石的体积=水面上升的体积,水面上升的体积可看作长为15厘米,宽为15厘米,高为(10.5-8)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【详解】15×15×(10.5-8)
=15×15×2.5
=225×2.5
=562.5(立方厘米)
答:珊瑚石的体积是562.5立方厘米。
【点睛】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式解决问题。
28.小时
【分析】用王芳做语文作业用的时间-做数学作业比语文作业少用的时间,即用-,即可求出她做数学作业用的时间。
【详解】-
=-
=(小时)
答:她做数学作业用了小时。
29.0.5立方分米
【分析】根据长方体的体积公式:V=abh,据此求出水槽中水和土豆的体积,再减去水的体积就是土豆的体积。
【详解】15厘米=1.5分米
5.5升=5.5立方分米
2×2×1.5-5.5
=4×1.5-5.5
=6-5.5
=0.5(立方分米)
答:这个土豆的体积是0.5立方分米。
【点睛】本题考查长方体的体积,熟记公式是解题的关键。
30.662平方米
【分析】贴瓷砖的面积是底面积和四个侧面的面积和。将长25米、宽20米、高1.8米代入“长×宽+(长×高+宽×高)×2”计算即可。
【详解】25×20+(25×1.8+20×1.8)×2
=500+(45+36)×2
=500+81×2
=500+162
=662(平方米)
答:需要662平方米瓷砖。
【点睛】在实际生活中,并不是所有的长方体形状的物体都有6个面,如长方体形状的鱼缸、游泳池等只有5个面,长方体形状的烟囱、通风管等只有4个面。
31.1120平方厘米
【分析】一个长方体饼干盒,长17厘米,宽11厘米,高20厘米,若给这个饼干盒的侧面贴满一圈包装纸,也就是求这个长方体的前后、左右4个面的面积,根据长方形的面积公式,求出这4个面的面积和即可。
【详解】17×20×2+11×20×2
=680+440
=1120(平方厘米)
答:包装纸的面积至少有1120平方厘米。
【点睛】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题.
答案第1页,共2页
答案第1页,共2页
一、选择题
1.一个数既是21的因数,又是21的倍数,这个数是( )。
A.1 B.3 C.7 D.21
2.最小的质数是( )。
A.2 B.3 C.4 D.1
3.下面适合用折线统计图表示的是( )。
A.小林0~18岁身高变化情况 B.阳光小学五年级各班人数情况
C.学校图书馆各类图书数量情况 D.甲、乙、丙、丁四个城市三月份平均气温情况
4.把20克糖放入180克水中,糖占糖水的( )。
A. B. C. D.
5.把一个长方体切成几个小长方体后,表面积( )。
A.不变 B.比原来大 C.比原来小
6.下面两个数是互质数的是( )。
A.3和12 B.4和6 C.5和21 D.7和42
7.如果小刚的体重是小东的,小明的体重是小东的,下面说法正确的是( )。
A.小刚比小明重 B.小明比小刚重 C.无法比较
8.在下图□中填上合适的分数,□中的分数是( )。
A. B. C. D.
9.一个长方体的底面是一个面积为16cm2的正方形,它的侧面展开图也是一个正方形。这个长方体的体积是( )cm3。
A.16 B.64 C.128 D.256
10.一个几何体如图,其中三角形面积为6cm2,它的体积是( )。
A.30cm3 B.60cm3 C.无法计算
二、填空题
11.在3,5和20这三个数中,( )是( )的倍数,( )是( )的因数。
12.用同样的小正方体摆几何体时,可以根据三个方向观察到的形状摆出原来的图形,有时候摆法也不是( )的。
13.一根铁丝长5米,平均分成6段,每段占全长的( ),每段长( )米。
14.0.68吨=( )千克;40分=( )时。
15.在括号里填上“>”“<”或“=”。
( ) ( ) 3.66÷1.1( )3.66
16.把一根4米长的绳子平均剪成6段,每段占这根绳子的( ),每段长( )米。
17.商店里有一些月饼,6块一盒或9块一盒,都正好装完。这些月饼至少有( )块。
18.35的因数有( ),100以内17的倍数有( )。
三、判断题
19.把一个分数的分子乘2,分母除以2,分数的大小不变。( )
20.下面是一位发烧病人一天测量体温的统计图,通过统计图我们可以发现这位病人是逐渐好转的。( )
21.一个病人打一次点滴的药水约是200升。( )
22.一块巧克力两人分,每人分到。( )
23.体积不相等的物体表面积一定不相等。( )
四、计算题
24.脱式计算。
(1) (2)
25.计算下列各题,怎样简便就怎样算。
五、解答题
26.王奶奶家养了10只鸡,养了7只鸭。鸭的数量是鸡的几分之几?
27.下图是实验小组的同学们测量珊瑚石体积的实验,请你用给出的数据计算珊瑚石的体积?
28.王芳做语文作业用了小时,做数学作业比语文作业少用了小时,她做数学作业用了多少小时?
29.一个长方体水槽,从里面量长、宽都是2分米,向水槽中倒入5.5升水,再把一块土豆放入水槽中,土豆完全浸没,这时量得水槽内水深15厘米,水没有溢出,这块土豆的体积是多少立方分米?
30.红星小区修建了一个长25米、宽20米、高1.8米的游泳池,给这个游泳池内部贴上瓷砖,需要多少平方米瓷砖?
31.一个长方体饼干盒,长17厘米,宽11厘米,高20厘米。如果在它的侧面贴满一圈包装纸(如图),包装纸的面积至少有多少平方厘米?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第1页,共3页
《期末测试》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A A A B C A C D B
1.D
【分析】根据找一个数的因数的方法:一个数的因数是有限的,最大的因数是它本身,最小的因数是1;根据找一个数的倍数的方法,一个数的倍数是无限的,最小的一个倍数是它本身,可见一个数的本身既是其最大因数又是其最小倍数。
【详解】由分析可知:
一个数既是21的因数,又是21的倍数,这个数是21。
故答案为:D
2.A
【分析】一个数的因数只有1和本身,那么它是质数,2是最小的质数。
【详解】最小的质数是2。
故答案为:A
【点睛】本题考查了质数,掌握质数的概念是解题的关键。
3.A
【分析】条形统计图以直条长短清晰表示各数据大小,无需复杂转换或计算,一眼就能判断数量多少;折线统计图能通过折线的上升或下降,清晰直观地展现数据是增加还是减少,通过折线统计图可一目了然看出走势。
【详解】A.小林0~18岁身高变化,需体现随时间推移身高的增减变化趋势,折线统计图通过连接数据点形成折线,能直观清晰地展示这种变化,所以该情况适合用折线统计图;
B.阳光小学五年级各班人数,重点在于直观呈现各班人数具体数值的多少,条形统计图以直条长短表示数量,在比较数量多少方面更具优势,因此该情况适合条形统计图而非折线统计图。
C.学校图书馆各类图书数量,主要是对比不同类别图书数量的多少,条形统计图能清晰展示数量差异,更契合此需求,不适合用折线统计图。
D.四个城市三月份平均气温,是要对同一时间不同城市的气温数值进行比较,条形统计图在呈现数量多少对比上更清晰明了,所以该情况更适合条形统计图 。
故答案为:A
4.A
【分析】糖是20克,糖水是(20+180)克,求糖占糖水的几分之几,实际是求一个数占另一个数的几分之几,用20除以(20+180)即可得解。
【详解】20÷(20+180)
=20÷200
=
故答案为:A
【点睛】此题的解题关键是根据分数的意义,掌握求一个数占另一个数的几分之几的计算方法。
5.B
【分析】表面积:物体露在外面的面积和,是物体的表面积,由于将长方体分成几个小长方体后,立体图形的面的数量增加,表面积相应的增大了,据此选择。
【详解】根据分析得,把一个长方体切成几个小长方体后,表面积比原来大。
故答案为:B
【点睛】本题考查了长方体的表面积,对立体图形表面积有清晰的认识是解题的关键。
6.C
【分析】公因数只有1的两个数,叫做互质数,如:5和7是互质数,7和13也是互质数,据此解答。
【详解】A.3和12的公因数有1,3,所以3和12不是互质数;
B.4和6的公因数有1,2,所以4和6不是互质数;
C.5和21只有公因数1,所以5和21是互质数;
D.7和42的公因数有1,7,所以7和42不是互质数。
故答案为:C
【点睛】掌握互质数的意义是解答题目的关键。
7.A
【分析】由题意可知,小刚的体重和小明的体重都和小东的体重有关。小刚的体重是小东的,小明的体重是小东的,可将分数转化成小数,比较大小,据此解答。
【详解】,
小刚的体重可表示为:小东的体重×0.75
小明的体重可表示为:小东的体重×0.6
0.75>0.6,所以,小刚比小明重。
故答案为:A
8.C
【分析】观察图可知:数轴中的每个大格表示0.1,平均分成10个小格,每一小格代表的数值为0.1的,据此在数轴上表示出题目中相应的分数即可。
【详解】由分析可得:□中的分数是;
故答案为:C
【点睛】掌握分数的意义是解题的关键。
9.D
【分析】由题意可知,长方体的长和宽都是4cm,它的高等于底面周长,根据,可求出高,再根据,代入数据计算即可。
【详解】
(cm3)
一个长方体的底面是一个面积为16cm2的正方形,它的侧面展开图也是一个正方形。这个长方体的体积是256cm3。
故答案为:D
10.B
【分析】图示的几何体和长方体、正方体有相似处,都是上下粗细一样大的柱体,根据长方体、正方体的体积公式V=Sh可知,这个几何体的体积也是V=Sh,代入数据计算即可。
【详解】6×10=60(cm3)
故答案为:B
【点睛】关键是由长方体、正方体的体积公式推出几何体的体积公式。
11. 20 5 5 20
【分析】在整数除法中,商是整数且没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,据此填空即可。
【详解】因为20÷5=4,所以20是5的倍数,5是20的因数。
【点睛】本题考查因数和倍数,明确因数和倍数的定义是解题的关键。
12.唯一
【分析】一个几何体从正面、左面、上面看到的形状,只是从它的三个不同方向看到的,不能反映它的全貌,所以根据从三个方向观察到的形状摆出原来的图形,有时候有几种摆法。
【详解】用同样的小正方体摆几何体时,可以根据三个方向观察到的形状摆出原来的图形,有时候摆法也不是唯一的。
【点睛】本题考查根据从不同方向观察几何体的平面图形还原立体图形,培养学生的空间想象力。
13.
【分析】先把这根铁丝看成单位“1”,平均分成6段,那么每段都是这根铁丝的;
这根铁丝总共5米长,每一段铁丝的长度就是米。
【详解】
(米)
所以每段占全长的,每段长米。
【点睛】考查分数的意义,重点是能够区分有单位的分数与没单位的分数的区别。
14. 680
【分析】(1)1吨=1000千克,高级单位转化成低级单位乘进率即可;
(2)1时=60分,低级单位转化成高级单位除以进率即可。
【详解】(1)0.68×1000=680(千克)
0.68吨=680千克
(2)40÷60=(时)
40分=时
15. < > <
【分析】将循环小数写成一般形式,再根据小数的大小比较方法,填出第一空;
将和先通分,再按照同分母分数的大小比较方法,比较大小,填出第二空;
一个数(0除外)除以一个大于1的数,商比原来的数小,据此填出第四空。
【详解】=0.506506…,=0.50666…,所以<;
=,=,所以>;
1.1>1,所以3.66÷1.1<3.66。
【点睛】本题考查了循环小数大小比较、分数大小比较以及商和被除数的关系,属于基础题,分析时需细心。
16.
【分析】把这条绳子的全长看作单位“1”,把“1”平均分成6段,用1除以6,即是每段占这根据绳子的几分之几,计算结果不带单位;
把4米长的绳子平均分成6段,用这根绳子的长度除以6,即是每段的长度,计算结果带单位。
【详解】1÷6=
4÷6=(米)
每段占这根绳子的,每段长米。
17.18
【分析】由题意可知,这些月饼的个数既是6的倍数,又是9的倍数时,刚好可以装完,求月饼的最少个数就是求这两个数的最小公倍数,据此解答。
【详解】
6和9的最小公倍数为:3×2×3=18
所以,这些月饼至少有18块。
【点睛】本题主要考查最小公倍数的应用,掌握求两个数最小公倍数的方法是解答题目的关键。
18. 1、5、7、35 17、34、51、68、85
【分析】根据求一个数因数和倍数的方法,分别求出35的因数及100 以内17的倍数即可。
【详解】35的因数有:1、5、7、35;
100以内17的倍数有:17、34、51、68、85。
【点睛】本题考查因数和倍数,明确求一个数的因数和倍数的方法是解题的关键。
19.×
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
【详解】把一个分数的分子乘2,分母也应乘2,分数的大小不变。
原题说法错误。
故答案为:×
【点睛】本题考查分数的基本性质的灵活运用。
20.√
【分析】折线统计图可以通过折线的上升和下降表示数量的增减变化情况,统计图中横轴表示测量体温的时间,纵轴表示病人的体温,表示体温的折线呈下降趋势,说明病人的体温正在下降并趋于正常体温,据此解答。
【详解】观察折线统计图可知,发烧病人的体温逐渐下降并趋于正常体温,说明这位病人病情逐渐好转。
故答案为:√
【点睛】掌握折线统计图的特征是解答题目的关键。
21.×
【分析】容积单位有升和毫升,其中升是较大的容积单位,毫升是较小的容积单位。1升水大约能倒满5个一次性纸杯,1毫升水只有十几滴。根据生活经验可知:计量一个病人打一次点滴的药水要选用较小的容积单位。
【详解】一个病人打一次点滴的药水约是200毫升。
故答案为:×
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
22.×
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数,据此解答。
【详解】一块巧克力两人分,没有说平均分,所以每人不一定都分到。
故答案为:×
【点睛】本题考查了分数的意义,注意用分数表示必须要平均分。
23.×
【分析】根据长方体的表面积公式和长方体的体积公式,通过举例论证题目中的说法是否正确。假设1号长方体的长为4厘米,宽为3厘米,高为2厘米,2号长方体的长为8厘米,宽为2厘米,高为1厘米,利用长方体的表面积和体积公式求出它们的表面积和体积,据此判断。
【详解】1号长方体表面积:(4×3+4×2+3×2)×2
=(12+8+6)×2
=26×2
=52(平方厘米)
2号长方体表面积:(8×2+8×1+2×1)×2
=(16+8+2)×2
=26×2
=52(平方厘米)
1号长方体的体积:4×3×2=24(立方厘米)
2号长方体的体积:8×2×1=16(立方厘米)
可见两个长方体的表面积相等,但这两个长方体的体积不相等。
所以原题中“体积不相等的物体表面积一定不相等”的说法是错误的。
故答案为:×
【点睛】此题考查的目的是理解掌握立体图形表面积、体积的计算方法及应用。
24.;
【分析】第一题先通分,再按照四则运算顺序先计算减法,最后算加法;
第二题利用减法的性质进行简便计算即可。
【详解】
=
=
=
=
=
=
=
25.;;0
【分析】(1)利用加法交换律简便计算;
(2)利用加法交换律和结合律简便计算;
(3)先去掉小括号,再利用减法性质简便计算。
【详解】(1)
=
=
=
(2)
=
=
=
(3)
=
=
=
=0
26.
【分析】求一个数是另一个数的几分之几用除法计算,商用分数表示即可。
【详解】7÷10=
答:鸭的数量是鸡的。
27.562.5立方厘米
【分析】珊瑚石完全浸没在水里后,珊瑚石的体积=水面上升的体积,水面上升的体积可看作长为15厘米,宽为15厘米,高为(10.5-8)厘米的长方体的体积,根据长方体的体积公式,把数据代入即可得解。
【详解】15×15×(10.5-8)
=15×15×2.5
=225×2.5
=562.5(立方厘米)
答:珊瑚石的体积是562.5立方厘米。
【点睛】此题的解题关键是掌握不规则物体的体积的计算方法,通过转化的数学思想,灵活运用长方体的体积公式解决问题。
28.小时
【分析】用王芳做语文作业用的时间-做数学作业比语文作业少用的时间,即用-,即可求出她做数学作业用的时间。
【详解】-
=-
=(小时)
答:她做数学作业用了小时。
29.0.5立方分米
【分析】根据长方体的体积公式:V=abh,据此求出水槽中水和土豆的体积,再减去水的体积就是土豆的体积。
【详解】15厘米=1.5分米
5.5升=5.5立方分米
2×2×1.5-5.5
=4×1.5-5.5
=6-5.5
=0.5(立方分米)
答:这个土豆的体积是0.5立方分米。
【点睛】本题考查长方体的体积,熟记公式是解题的关键。
30.662平方米
【分析】贴瓷砖的面积是底面积和四个侧面的面积和。将长25米、宽20米、高1.8米代入“长×宽+(长×高+宽×高)×2”计算即可。
【详解】25×20+(25×1.8+20×1.8)×2
=500+(45+36)×2
=500+81×2
=500+162
=662(平方米)
答:需要662平方米瓷砖。
【点睛】在实际生活中,并不是所有的长方体形状的物体都有6个面,如长方体形状的鱼缸、游泳池等只有5个面,长方体形状的烟囱、通风管等只有4个面。
31.1120平方厘米
【分析】一个长方体饼干盒,长17厘米,宽11厘米,高20厘米,若给这个饼干盒的侧面贴满一圈包装纸,也就是求这个长方体的前后、左右4个面的面积,根据长方形的面积公式,求出这4个面的面积和即可。
【详解】17×20×2+11×20×2
=680+440
=1120(平方厘米)
答:包装纸的面积至少有1120平方厘米。
【点睛】解答有关长方体计算的实际问题,一定要搞清所求的是什么,再进一步选择合理的计算方法进行计算解答问题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
